【湘教版数学九年级上册同步练习】 第三章图形的相似综合检测题(含答案)
文档属性
| 名称 | 【湘教版数学九年级上册同步练习】 第三章图形的相似综合检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 16:09:09 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【湘教版数学九年级上册同步练习】
第三章图形的相似综合检测题
一、单选题
1.如图,AD,BC相交于点O,由下列条件仍不能判定△AOB与△DOC相似的是( )
A.AB∥CD B.∠C=∠B C. D.
2.如图,已知△ABC,任取一点O,连AO,BO,CO,分别取点D,E,F,使OD= AO,OE= BO,OF= CO,得△DEF,有下列说法:
①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;
③△DEF与△ABC的周长比为1:3;④△DEF与△ABC的面积比为1:6.
则正确的个数是( )
A.1 B.2 C.3 D.4
3.若 且相似比为1:4,则 与 的面积比为( )
A.1:4 B.4:1 C.1:16 D.16:1
4.如图,已知AB∥CD∥EF,BC:CE=3:4,AF=21,那么DF的长为( )
A.9 B.12 C.15 D.18
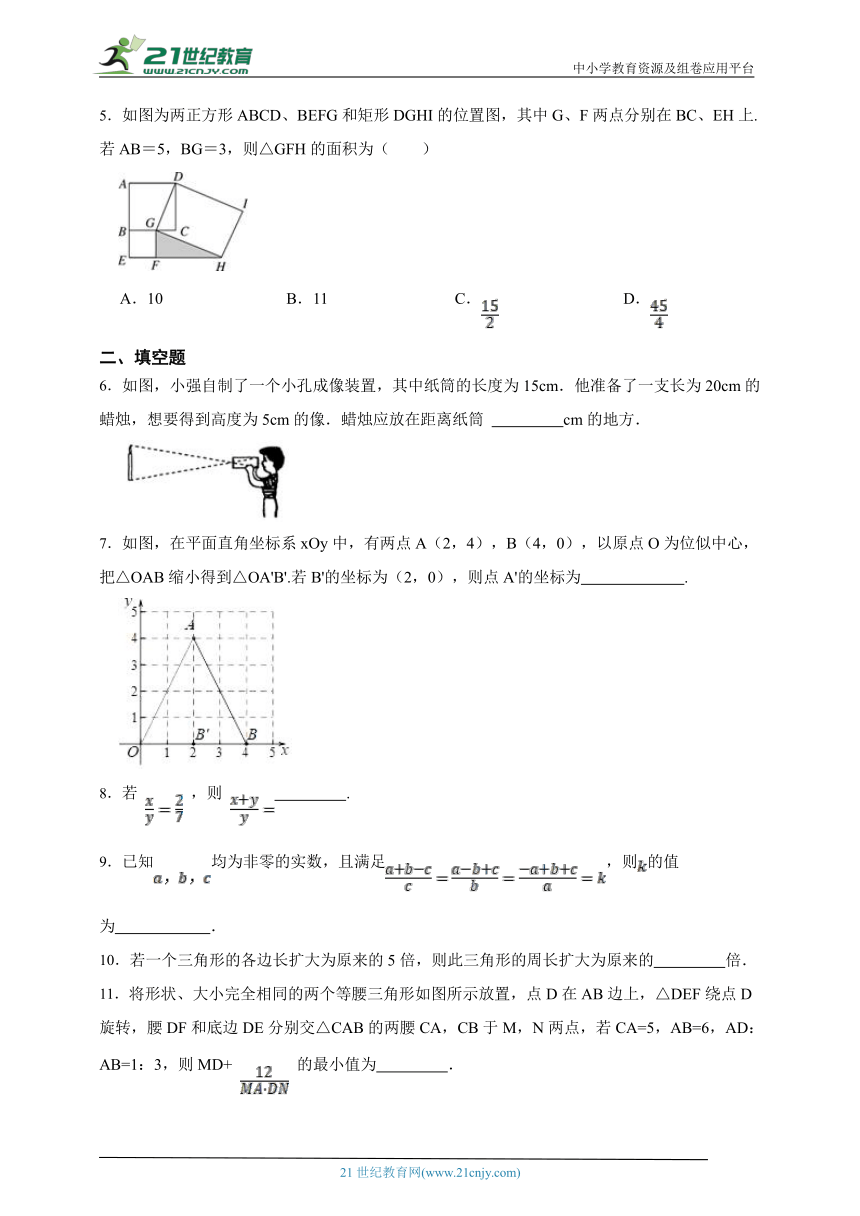
5.如图为两正方形ABCD、BEFG和矩形DGHI的位置图,其中G、F两点分别在BC、EH上.若AB=5,BG=3,则△GFH的面积为( )
A.10 B.11 C. D.
二、填空题
6.如图,小强自制了一个小孔成像装置,其中纸筒的长度为15cm.他准备了一支长为20cm的蜡烛,想要得到高度为5cm的像.蜡烛应放在距离纸筒 cm的地方.
7.如图,在平面直角坐标系xOy中,有两点A(2,4),B(4,0),以原点O为位似中心,把△OAB缩小得到△OA'B'.若B'的坐标为(2,0),则点A'的坐标为 .
8.若 ,则 .
9.已知均为非零的实数,且满足,则的值为 .
10.若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的 倍.
11.将形状、大小完全相同的两个等腰三角形如图所示放置,点D在AB边上,△DEF绕点D旋转,腰DF和底边DE分别交△CAB的两腰CA,CB于M,N两点,若CA=5,AB=6,AD:AB=1:3,则MD+ 的最小值为 .
三、计算题
12.已知 = ,求 的值.
13.【问题情境】
如图,在四边形中,,,,点是线段上一动点,连接.将线段绕点逆时针旋转,且长度变为原来的倍,得到线段,作直线交直线于点.数学兴趣小组着手研究为何值时,的值是定值.
【探究实践】
老师引导同学们可以先通过边、角的特殊化,发现的取值与为定值的关系,再探究图中的问题,这体现了从特殊到一般的数学思想.
经过思考和讨论,小明、小华分享了自己的发现.
(1)如图,小明发现:“当,时,点与点恰好重合,的值是定值”.小华给出了解题思路,连接,易证,得到与的数量关系是 ,的值是 ;
(2)如图,小华发现:“当,时,的值是定值”.请判断小明的结论是否正确,若正确,请求出此定值,若不正确,请说明理由;
【拓展应用】
(3)如图,小聪对比小明和小华的发现,经过进一步思考发现:“连接,只要确定的长,就能求出的值,使得的值是定值”,老师肯定了小聪结论的准确性.若,请直接写出的值及的定值.
四、解答题
14.已知△ABC中,AB=15cm,BC=21cm,AC=30cm,另一个与它相似的△A′B′C′的最长边长为40cm,求△A′B′C′的其余两边的长.
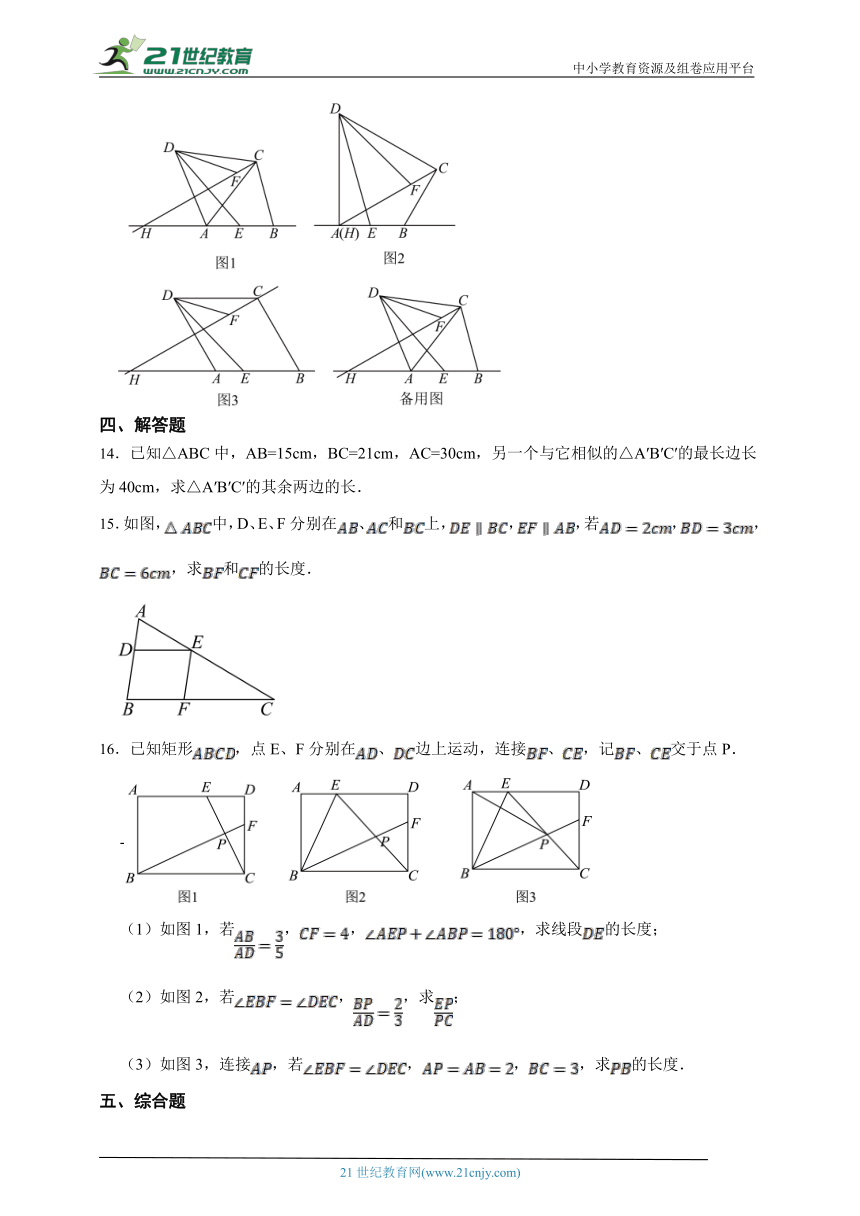
15.如图,中,D、E、F分别在、和上,,,若,,,求和的长度.
16.已知矩形,点E、F分别在、边上运动,连接、,记、交于点P.
-
(1)如图1,若,,,求线段的长度;
(2)如图2,若,,求;
(3)如图3,连接,若,,,求的长度.
五、综合题
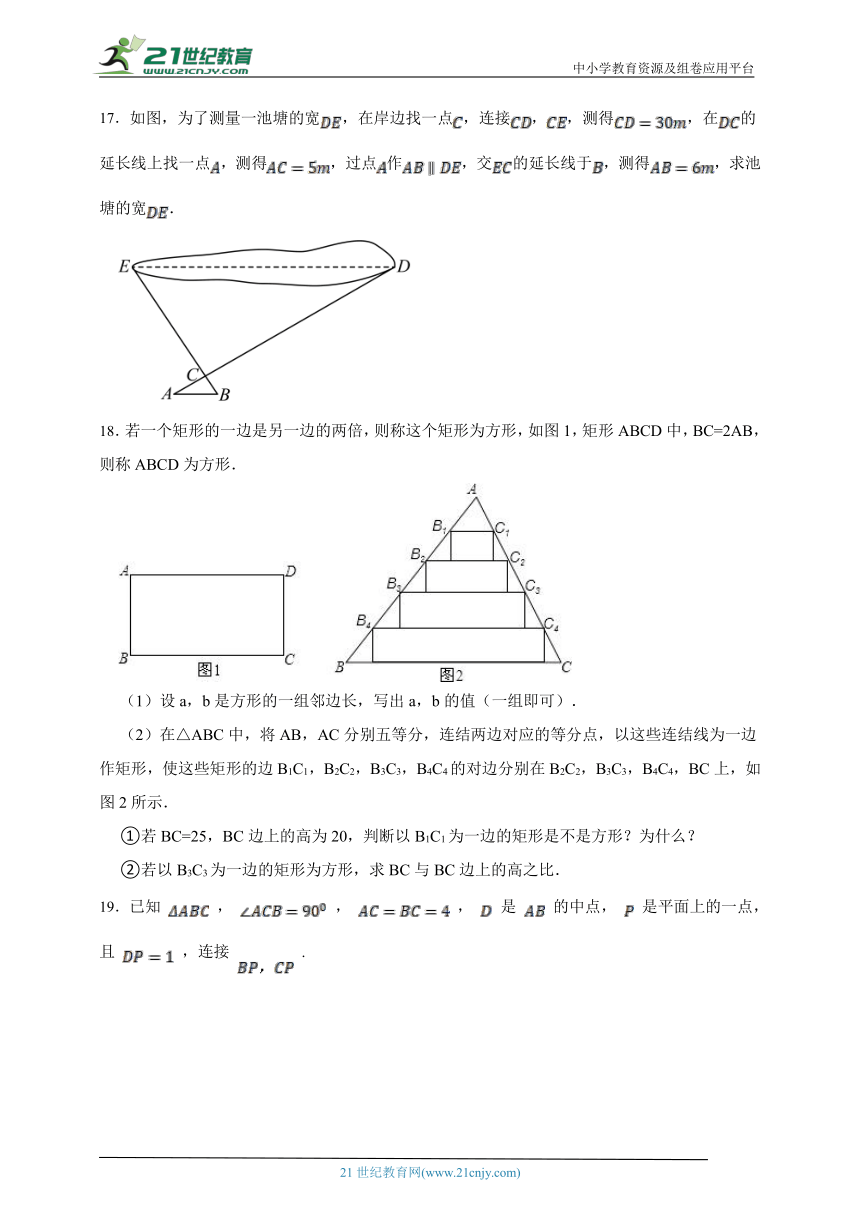
17.如图,为了测量一池塘的宽,在岸边找一点,连接,,测得,在的延长线上找一点,测得,过点作,交的延长线于,测得,求池塘的宽.
18.若一个矩形的一边是另一边的两倍,则称这个矩形为方形,如图1,矩形ABCD中,BC=2AB,则称ABCD为方形.
(1)设a,b是方形的一组邻边长,写出a,b的值(一组即可).
(2)在△ABC中,将AB,AC分别五等分,连结两边对应的等分点,以这些连结线为一边作矩形,使这些矩形的边B1C1,B2C2,B3C3,B4C4的对边分别在B2C2,B3C3,B4C4,BC上,如图2所示.
①若BC=25,BC边上的高为20,判断以B1C1为一边的矩形是不是方形?为什么?
②若以B3C3为一边的矩形为方形,求BC与BC边上的高之比.
19.已知 , , , 是 的中点, 是平面上的一点,且 ,连接 .
(1)如图,当点 在线段 上时,求 的长;
(2)当 是等腰三角形时,求 的长;
(3)将点 绕点 顺时针旋转 得到点 ,连接 ,求 的最大值.
六、实践探究题
20.综合实践活动
主题:测量墙面高度
素材:手电筒,木板,平面镜,直尺
步骤:如图,小颖同学手持电筒从点A处发射光线,通过水平放置在地面上的平面镜C反射后,经过垂直于地面放置的木板上边缘点D,落在垂直于地面的墙面F处,小颖测得A处离地面的高度,B处离木板底端E处的长度,E处到墙面底端G处的长度,木板长度.
计算:已知光通过平面镜反射中入射角等于反射角,图中点B,C,E,G在同一水平线上.求点F到地面的高度FG.
答案解析部分
1.【答案】D
【知识点】相似三角形的判定
2.【答案】C
【知识点】相似三角形的判定与性质;位似变换
3.【答案】C
【知识点】相似三角形的性质
4.【答案】B
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
5.【答案】D
【知识点】三角形的面积;矩形的性质;正方形的性质;相似三角形的判定与性质
6.【答案】60
【知识点】相似三角形的应用
7.【答案】(1,2)
【知识点】位似变换
8.【答案】
【知识点】比例的性质
9.【答案】或
【知识点】分式的化简求值;比例的性质
10.【答案】5
【知识点】相似三角形的性质
11.【答案】
【知识点】等腰三角形的性质;相似三角形的判定与性质;旋转的性质
12.【答案】解:由 = ,得 = b.
∴
【知识点】分式的基本性质;比例的性质
13.【答案】(1),;(2)的值是定值,;(3),.
【知识点】等边三角形的判定与性质;勾股定理;相似三角形的判定与性质;旋转的性质
14.【答案】解:设△A′B′C′的其余两边的长度分别是x,y,
根据题意,得 = , = ,
解得x=20,y=28,
答:△A′B′C的其余两边的长分别是20cm和28cm.
【知识点】相似三角形的判定与性质
15.【答案】,
【知识点】平行四边形的性质;相似三角形的判定与性质
16.【答案】(1)
(2)
(3)
【知识点】矩形的性质;相似三角形的判定与性质
17.【答案】
【知识点】相似三角形的应用
18.【答案】(1)解:答案不唯一,如a=2,b=4
(2)解:①以B1C1为一边的矩形不是方形.
理由是:过A作AM⊥BC于M,交B1C1于E,交B2C2于H,交B3C3于G,交B4C4于N,则AM⊥B4C4,AM⊥B3C3,AM⊥B2C2,AM⊥B1C1,
∵由矩形的性质得:BC∥B1C1∥B2C2∥B3C3∥B4C4,
∴△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4,
∴ = , = , = , = = ,
∵AM=20,BC=25,
∴B1C1=5,B2C2=10,B3C3=15,B4C4=20,AE=4,AH=8,AG=12,AN=16,
∴MN=GN=GH=HE=4,
∴B1Q=B2O=B3Z=B4K=4,
即B1C1≠2B1Q,B1Q≠2B1C1,
∴以B1C1为一边的矩形不是方形;
②∵以B3C3为一边的矩形为方形,设AM=h,
∴△ABC∽△AB3C3,
∴ = ,
则AG= h,
∴MN=GN=GH=HE= h,
当B3C3=2× h时, = = ;
当B3C3= × h时, = = .
综合上述:BC与BC边上的高之比是 或 .
【知识点】相似三角形的判定与性质
19.【答案】(1)解:如图1中,连接 .
在 中, , ,
∴ ,
∵ ,
∴ , ,
在 中,
(2)解:如图2中,∵ ,
∴点 在以点 为圆心的⊙ 上.
①当 时,
∵ ,
∴ 都在线段 的垂直平分线上,设直线 交 于 .
∴ , ,
∵ ,
∴ ,
在 中, ,
当 在线段 上时, , ,
当 在线段 的延长线上时, , .
②当 时,∵ ,
∴ ,此种情形不存在;
③当 时,同理这种情形不存在;
如图3中
(3)解:如图4中,连接 .
由旋转可知: , ,
∴ ,
∴ ,
∴ ,
∵ , ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ∽ ,
∴ ,
∵ ,
∴点 落在 的延长线与⊙ 的交点处, 的值最大,
∴ .
∴ 的最大值为 .
【知识点】三角形三边关系;勾股定理;相似三角形的判定与性质;旋转的性质;直角三角形斜边上的中线
20.【答案】解:∵光在镜面反射中的入射角等于反射角,
∴.
又∵,
∴,
∴.
∵,,,
∴
∴,
由题意得,
则.
∴.
∵,
∴.
解得
答:点F到地面的高度FG为5.76m
【知识点】相似三角形的应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【湘教版数学九年级上册同步练习】
第三章图形的相似综合检测题
一、单选题
1.如图,AD,BC相交于点O,由下列条件仍不能判定△AOB与△DOC相似的是( )
A.AB∥CD B.∠C=∠B C. D.
2.如图,已知△ABC,任取一点O,连AO,BO,CO,分别取点D,E,F,使OD= AO,OE= BO,OF= CO,得△DEF,有下列说法:
①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;
③△DEF与△ABC的周长比为1:3;④△DEF与△ABC的面积比为1:6.
则正确的个数是( )
A.1 B.2 C.3 D.4
3.若 且相似比为1:4,则 与 的面积比为( )
A.1:4 B.4:1 C.1:16 D.16:1
4.如图,已知AB∥CD∥EF,BC:CE=3:4,AF=21,那么DF的长为( )
A.9 B.12 C.15 D.18
5.如图为两正方形ABCD、BEFG和矩形DGHI的位置图,其中G、F两点分别在BC、EH上.若AB=5,BG=3,则△GFH的面积为( )
A.10 B.11 C. D.
二、填空题
6.如图,小强自制了一个小孔成像装置,其中纸筒的长度为15cm.他准备了一支长为20cm的蜡烛,想要得到高度为5cm的像.蜡烛应放在距离纸筒 cm的地方.
7.如图,在平面直角坐标系xOy中,有两点A(2,4),B(4,0),以原点O为位似中心,把△OAB缩小得到△OA'B'.若B'的坐标为(2,0),则点A'的坐标为 .
8.若 ,则 .
9.已知均为非零的实数,且满足,则的值为 .
10.若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的 倍.
11.将形状、大小完全相同的两个等腰三角形如图所示放置,点D在AB边上,△DEF绕点D旋转,腰DF和底边DE分别交△CAB的两腰CA,CB于M,N两点,若CA=5,AB=6,AD:AB=1:3,则MD+ 的最小值为 .
三、计算题
12.已知 = ,求 的值.
13.【问题情境】
如图,在四边形中,,,,点是线段上一动点,连接.将线段绕点逆时针旋转,且长度变为原来的倍,得到线段,作直线交直线于点.数学兴趣小组着手研究为何值时,的值是定值.
【探究实践】
老师引导同学们可以先通过边、角的特殊化,发现的取值与为定值的关系,再探究图中的问题,这体现了从特殊到一般的数学思想.
经过思考和讨论,小明、小华分享了自己的发现.
(1)如图,小明发现:“当,时,点与点恰好重合,的值是定值”.小华给出了解题思路,连接,易证,得到与的数量关系是 ,的值是 ;
(2)如图,小华发现:“当,时,的值是定值”.请判断小明的结论是否正确,若正确,请求出此定值,若不正确,请说明理由;
【拓展应用】
(3)如图,小聪对比小明和小华的发现,经过进一步思考发现:“连接,只要确定的长,就能求出的值,使得的值是定值”,老师肯定了小聪结论的准确性.若,请直接写出的值及的定值.
四、解答题
14.已知△ABC中,AB=15cm,BC=21cm,AC=30cm,另一个与它相似的△A′B′C′的最长边长为40cm,求△A′B′C′的其余两边的长.
15.如图,中,D、E、F分别在、和上,,,若,,,求和的长度.
16.已知矩形,点E、F分别在、边上运动,连接、,记、交于点P.
-
(1)如图1,若,,,求线段的长度;
(2)如图2,若,,求;
(3)如图3,连接,若,,,求的长度.
五、综合题
17.如图,为了测量一池塘的宽,在岸边找一点,连接,,测得,在的延长线上找一点,测得,过点作,交的延长线于,测得,求池塘的宽.
18.若一个矩形的一边是另一边的两倍,则称这个矩形为方形,如图1,矩形ABCD中,BC=2AB,则称ABCD为方形.
(1)设a,b是方形的一组邻边长,写出a,b的值(一组即可).
(2)在△ABC中,将AB,AC分别五等分,连结两边对应的等分点,以这些连结线为一边作矩形,使这些矩形的边B1C1,B2C2,B3C3,B4C4的对边分别在B2C2,B3C3,B4C4,BC上,如图2所示.
①若BC=25,BC边上的高为20,判断以B1C1为一边的矩形是不是方形?为什么?
②若以B3C3为一边的矩形为方形,求BC与BC边上的高之比.
19.已知 , , , 是 的中点, 是平面上的一点,且 ,连接 .
(1)如图,当点 在线段 上时,求 的长;
(2)当 是等腰三角形时,求 的长;
(3)将点 绕点 顺时针旋转 得到点 ,连接 ,求 的最大值.
六、实践探究题
20.综合实践活动
主题:测量墙面高度
素材:手电筒,木板,平面镜,直尺
步骤:如图,小颖同学手持电筒从点A处发射光线,通过水平放置在地面上的平面镜C反射后,经过垂直于地面放置的木板上边缘点D,落在垂直于地面的墙面F处,小颖测得A处离地面的高度,B处离木板底端E处的长度,E处到墙面底端G处的长度,木板长度.
计算:已知光通过平面镜反射中入射角等于反射角,图中点B,C,E,G在同一水平线上.求点F到地面的高度FG.
答案解析部分
1.【答案】D
【知识点】相似三角形的判定
2.【答案】C
【知识点】相似三角形的判定与性质;位似变换
3.【答案】C
【知识点】相似三角形的性质
4.【答案】B
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
5.【答案】D
【知识点】三角形的面积;矩形的性质;正方形的性质;相似三角形的判定与性质
6.【答案】60
【知识点】相似三角形的应用
7.【答案】(1,2)
【知识点】位似变换
8.【答案】
【知识点】比例的性质
9.【答案】或
【知识点】分式的化简求值;比例的性质
10.【答案】5
【知识点】相似三角形的性质
11.【答案】
【知识点】等腰三角形的性质;相似三角形的判定与性质;旋转的性质
12.【答案】解:由 = ,得 = b.
∴
【知识点】分式的基本性质;比例的性质
13.【答案】(1),;(2)的值是定值,;(3),.
【知识点】等边三角形的判定与性质;勾股定理;相似三角形的判定与性质;旋转的性质
14.【答案】解:设△A′B′C′的其余两边的长度分别是x,y,
根据题意,得 = , = ,
解得x=20,y=28,
答:△A′B′C的其余两边的长分别是20cm和28cm.
【知识点】相似三角形的判定与性质
15.【答案】,
【知识点】平行四边形的性质;相似三角形的判定与性质
16.【答案】(1)
(2)
(3)
【知识点】矩形的性质;相似三角形的判定与性质
17.【答案】
【知识点】相似三角形的应用
18.【答案】(1)解:答案不唯一,如a=2,b=4
(2)解:①以B1C1为一边的矩形不是方形.
理由是:过A作AM⊥BC于M,交B1C1于E,交B2C2于H,交B3C3于G,交B4C4于N,则AM⊥B4C4,AM⊥B3C3,AM⊥B2C2,AM⊥B1C1,
∵由矩形的性质得:BC∥B1C1∥B2C2∥B3C3∥B4C4,
∴△ABC∽△AB1C1∽△AB2C2∽△AB3C3∽△AB4C4,
∴ = , = , = , = = ,
∵AM=20,BC=25,
∴B1C1=5,B2C2=10,B3C3=15,B4C4=20,AE=4,AH=8,AG=12,AN=16,
∴MN=GN=GH=HE=4,
∴B1Q=B2O=B3Z=B4K=4,
即B1C1≠2B1Q,B1Q≠2B1C1,
∴以B1C1为一边的矩形不是方形;
②∵以B3C3为一边的矩形为方形,设AM=h,
∴△ABC∽△AB3C3,
∴ = ,
则AG= h,
∴MN=GN=GH=HE= h,
当B3C3=2× h时, = = ;
当B3C3= × h时, = = .
综合上述:BC与BC边上的高之比是 或 .
【知识点】相似三角形的判定与性质
19.【答案】(1)解:如图1中,连接 .
在 中, , ,
∴ ,
∵ ,
∴ , ,
在 中,
(2)解:如图2中,∵ ,
∴点 在以点 为圆心的⊙ 上.
①当 时,
∵ ,
∴ 都在线段 的垂直平分线上,设直线 交 于 .
∴ , ,
∵ ,
∴ ,
在 中, ,
当 在线段 上时, , ,
当 在线段 的延长线上时, , .
②当 时,∵ ,
∴ ,此种情形不存在;
③当 时,同理这种情形不存在;
如图3中
(3)解:如图4中,连接 .
由旋转可知: , ,
∴ ,
∴ ,
∴ ,
∵ , ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ∽ ,
∴ ,
∵ ,
∴点 落在 的延长线与⊙ 的交点处, 的值最大,
∴ .
∴ 的最大值为 .
【知识点】三角形三边关系;勾股定理;相似三角形的判定与性质;旋转的性质;直角三角形斜边上的中线
20.【答案】解:∵光在镜面反射中的入射角等于反射角,
∴.
又∵,
∴,
∴.
∵,,,
∴
∴,
由题意得,
则.
∴.
∵,
∴.
解得
答:点F到地面的高度FG为5.76m
【知识点】相似三角形的应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
