2023-2024学年广东省惠州市惠东县七年级(下)期末数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年广东省惠州市惠东县七年级(下)期末数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 80.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 17:33:11 | ||
图片预览




文档简介
2023-2024学年广东省惠州市惠东县七年级(下)期末数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列图案中,可以通过其中一个基础图形平移得到的是( )
A. B. C. D.
2.下列实数是无理数的是( )
A. B. C. D.
3.在平面直角坐标系中,下列各点在第四象限的是( )
A. B. C. D.
4.下列各式中,属于二元一次方程的是( )
A. B. C. D.
5.下列调查案例中,最适宜采用全面调查普查方式的是( )
A. 调查惠州市中学生的视力状况 B. 检测神舟十六号飞船的零部件
C. 调查某河域的水污染情况 D. 调查一批节能灯的使用寿命
6.如图,直线、被直线所截,下列说法不正确的是( )
A. 和是同位角
B. 和是内错角
C. 和是对顶角
D. 和是邻补角
7.已知,下列四个不等式中,正确的是( )
A. B. C. D.
8.用代入法解方程组时,把代入后得到的方程是( )
A. B. C. D.
9.年月日,横琴马拉松在广东珠海横琴金融岛中央公园开跑小强跑在小海前面,在离终点时,他以的速度向终点冲刺,而此时小海在他身后,请问小海需以多快的速度同时冲刺,才能在小强之前到达终点?设此时小海冲刺的速度为,可列的不等式为( )
A. B.
C. D.
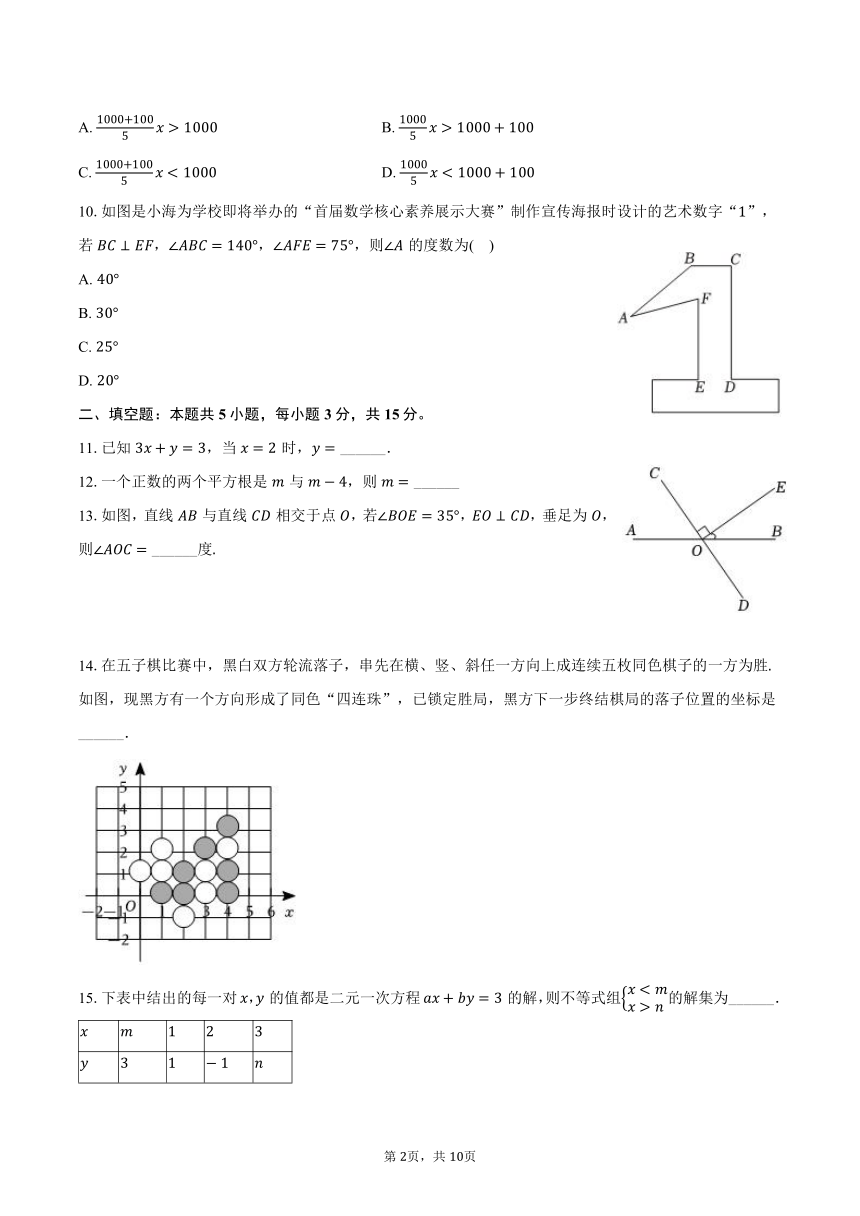
10.如图是小海为学校即将举办的“首届数学核心素养展示大赛”制作宣传海报时设计的艺术数字“”,若,,,则的度数为( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
11.已知,当时, ______.
12.一个正数的两个平方根是与,则 ______
13.如图,直线与直线相交于点,若,,垂足为,则 ______度
14.在五子棋比赛中,黑白双方轮流落子,串先在横、竖、斜任一方向上成连续五枚同色棋子的一方为胜如图,现黑方有一个方向形成了同色“四连珠”,已锁定胜局,黑方下一步终结棋局的落子位置的坐标是______.
15.下表中结出的每一对,的值都是二元一次方程的解,则不等式组的解集为______.
三、解答题:本题共6小题,共57分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:;
解不等式组并写出所有整数解.
17.本小题分
在正方形网格中,每个小正方形的边长均为个单位长度,三角形的三个顶点的位置如图所示,现将三角形平移,使点移动到点,点、分别是、的对应点.
请画出平移后的三角形;
连接、,直接写出线段与线段的关系:______.
18.本小题分
已知:如图,、分别平分和,求证:
证明:、分别平分和已知
______,
____________
______,
______
______.
______
19.本小题分
如图,已知,.
求证:;
若,,求的度数.
20.本小题分
我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法例如,代数式的几何意义是数轴上所对应的点与所对应的点之间的距离:因为,所以的几何意义就是数轴上所对应的点与所对应的点之间的距离.
(ⅰ)发现问题:代数式的最小值是多少?
(ⅱ)探究问题:如图,点、、分别表示数、、,.
的几何意义是线段与的长度之和,
当点在线段上时,,当点在点的左侧或点的右侧时,.
的最小值是.
请你根据上述自学材料,探究解决下列问题:
解决问题:的最小值是______;
利用上述思想方法解不等式:;
当为何值时,代数式的最小值是.
21.本小题分
如图,在平面直角坐标系中,直线与坐标轴交于,两点,点,在直线上我们可以用面积法求点的坐标.
问题探究:
请阅读并填空:
一方面,过点作轴于点,我们可以由,的坐标,直接得出三角形的面积为______平方单位;
另一方面,过点作轴于点,三角形的面积,三角形的面积 ______平方单位.
三角形的面积三角形的面积三角形的面积,
可得关于的一元一次方程为______,
解这个方程,可得点的坐标为______.
问题迁移:
如图,请你仿照中的方法,求点的纵坐标.
问题拓展:
若点在直线上,且三角形的面积等于平方单位,请直接写出点的坐标.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.或
15.
16.解:原式
;
解不等式,得
解不等式,得
不等式组的解集是
不等式组的所有整数解是,.
17.如图,为所作;
平行且相等.
18.证明:、分别平分和已知,
,
角平分线的定义,
已知,
两直线平行,内错角相等,
,
内错角相等,两直线平行.
19.证明:,
,
,
又,
,
;
解:,
,
,
,
,,
,
,
.
.
20.;
如图所示,满足,表示到和距离之和大于的范围,
当点在和之间时,距离之和为,不满足题意;
当点在的左边或的右边时,距离之和大于,
则范围为或;
当为或时,代数式为或,
数轴上表示数的点到表示数的点的距离为,数轴上表示数的点到表示数的点的距离也为,
因此当为或时,原式的最小值是.
21.,,,;
过点作轴于点,轴于点,连接,
则的面积为平方单位,
的面积为平方单位,
的面积为平方单位,
的面积的面积的面积,
,
解得,
点纵坐标为;
的面积为,
三角形的面积等于平方单位,
,
,
当点在轴右侧的直线上时,如图所示:
的面积为平方单位,
的面积为平方单位,
的面积为平方单位,
的面积的面积的面积,
,
解得,
点坐标为;
当点在轴左侧的直线上时,如图所示:
的面积为平方单位,的面积为平方单位,的面积为平方单位,
的面积的面积的面积,
,
解得,
点坐标为,
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列图案中,可以通过其中一个基础图形平移得到的是( )
A. B. C. D.
2.下列实数是无理数的是( )
A. B. C. D.
3.在平面直角坐标系中,下列各点在第四象限的是( )
A. B. C. D.
4.下列各式中,属于二元一次方程的是( )
A. B. C. D.
5.下列调查案例中,最适宜采用全面调查普查方式的是( )
A. 调查惠州市中学生的视力状况 B. 检测神舟十六号飞船的零部件
C. 调查某河域的水污染情况 D. 调查一批节能灯的使用寿命
6.如图,直线、被直线所截,下列说法不正确的是( )
A. 和是同位角
B. 和是内错角
C. 和是对顶角
D. 和是邻补角
7.已知,下列四个不等式中,正确的是( )
A. B. C. D.
8.用代入法解方程组时,把代入后得到的方程是( )
A. B. C. D.
9.年月日,横琴马拉松在广东珠海横琴金融岛中央公园开跑小强跑在小海前面,在离终点时,他以的速度向终点冲刺,而此时小海在他身后,请问小海需以多快的速度同时冲刺,才能在小强之前到达终点?设此时小海冲刺的速度为,可列的不等式为( )
A. B.
C. D.
10.如图是小海为学校即将举办的“首届数学核心素养展示大赛”制作宣传海报时设计的艺术数字“”,若,,,则的度数为( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
11.已知,当时, ______.
12.一个正数的两个平方根是与,则 ______
13.如图,直线与直线相交于点,若,,垂足为,则 ______度
14.在五子棋比赛中,黑白双方轮流落子,串先在横、竖、斜任一方向上成连续五枚同色棋子的一方为胜如图,现黑方有一个方向形成了同色“四连珠”,已锁定胜局,黑方下一步终结棋局的落子位置的坐标是______.
15.下表中结出的每一对,的值都是二元一次方程的解,则不等式组的解集为______.
三、解答题:本题共6小题,共57分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:;
解不等式组并写出所有整数解.
17.本小题分
在正方形网格中,每个小正方形的边长均为个单位长度,三角形的三个顶点的位置如图所示,现将三角形平移,使点移动到点,点、分别是、的对应点.
请画出平移后的三角形;
连接、,直接写出线段与线段的关系:______.
18.本小题分
已知:如图,、分别平分和,求证:
证明:、分别平分和已知
______,
____________
______,
______
______.
______
19.本小题分
如图,已知,.
求证:;
若,,求的度数.
20.本小题分
我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法例如,代数式的几何意义是数轴上所对应的点与所对应的点之间的距离:因为,所以的几何意义就是数轴上所对应的点与所对应的点之间的距离.
(ⅰ)发现问题:代数式的最小值是多少?
(ⅱ)探究问题:如图,点、、分别表示数、、,.
的几何意义是线段与的长度之和,
当点在线段上时,,当点在点的左侧或点的右侧时,.
的最小值是.
请你根据上述自学材料,探究解决下列问题:
解决问题:的最小值是______;
利用上述思想方法解不等式:;
当为何值时,代数式的最小值是.
21.本小题分
如图,在平面直角坐标系中,直线与坐标轴交于,两点,点,在直线上我们可以用面积法求点的坐标.
问题探究:
请阅读并填空:
一方面,过点作轴于点,我们可以由,的坐标,直接得出三角形的面积为______平方单位;
另一方面,过点作轴于点,三角形的面积,三角形的面积 ______平方单位.
三角形的面积三角形的面积三角形的面积,
可得关于的一元一次方程为______,
解这个方程,可得点的坐标为______.
问题迁移:
如图,请你仿照中的方法,求点的纵坐标.
问题拓展:
若点在直线上,且三角形的面积等于平方单位,请直接写出点的坐标.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.或
15.
16.解:原式
;
解不等式,得
解不等式,得
不等式组的解集是
不等式组的所有整数解是,.
17.如图,为所作;
平行且相等.
18.证明:、分别平分和已知,
,
角平分线的定义,
已知,
两直线平行,内错角相等,
,
内错角相等,两直线平行.
19.证明:,
,
,
又,
,
;
解:,
,
,
,
,,
,
,
.
.
20.;
如图所示,满足,表示到和距离之和大于的范围,
当点在和之间时,距离之和为,不满足题意;
当点在的左边或的右边时,距离之和大于,
则范围为或;
当为或时,代数式为或,
数轴上表示数的点到表示数的点的距离为,数轴上表示数的点到表示数的点的距离也为,
因此当为或时,原式的最小值是.
21.,,,;
过点作轴于点,轴于点,连接,
则的面积为平方单位,
的面积为平方单位,
的面积为平方单位,
的面积的面积的面积,
,
解得,
点纵坐标为;
的面积为,
三角形的面积等于平方单位,
,
,
当点在轴右侧的直线上时,如图所示:
的面积为平方单位,
的面积为平方单位,
的面积为平方单位,
的面积的面积的面积,
,
解得,
点坐标为;
当点在轴左侧的直线上时,如图所示:
的面积为平方单位,的面积为平方单位,的面积为平方单位,
的面积的面积的面积,
,
解得,
点坐标为,
第1页,共1页
同课章节目录
