【湘教版数学九年级上册同步练习】 4.2正切(含答案)
文档属性
| 名称 | 【湘教版数学九年级上册同步练习】 4.2正切(含答案) | 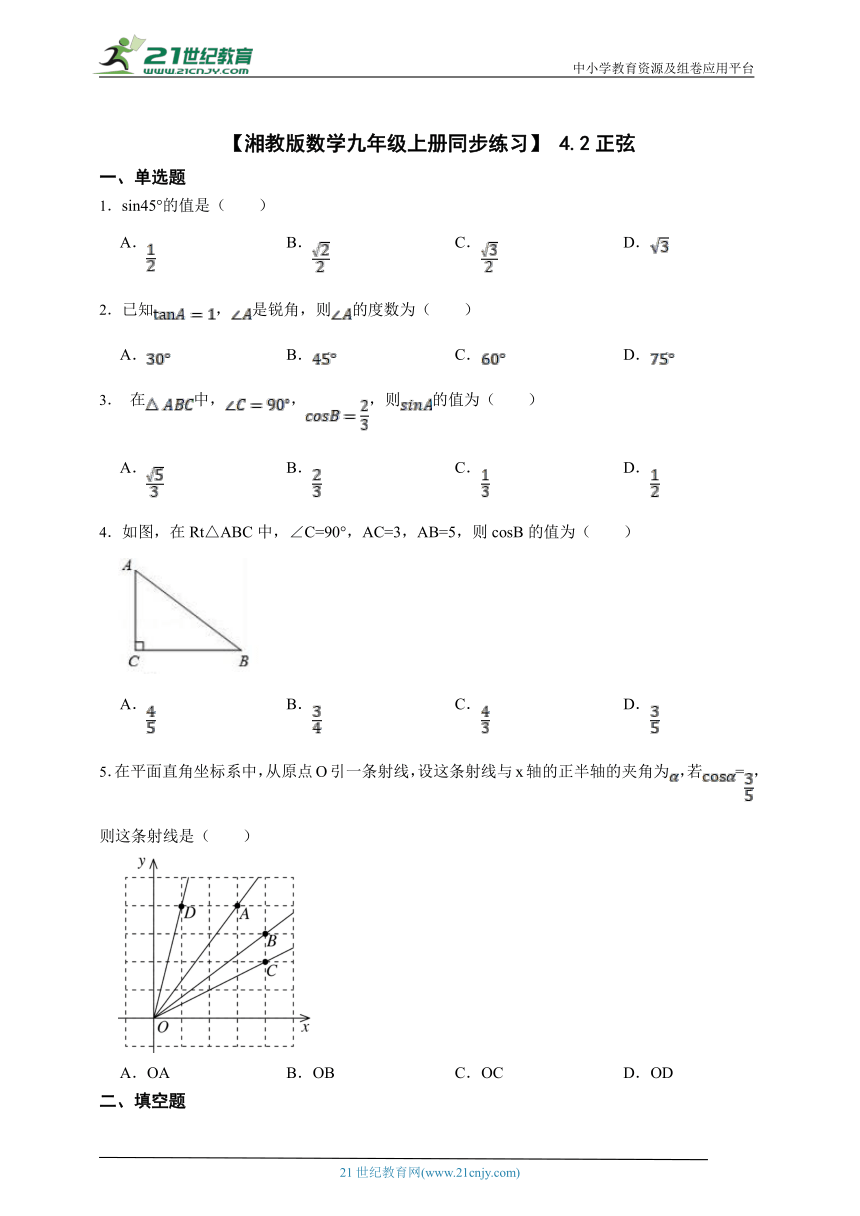 | |
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 16:12:45 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【湘教版数学九年级上册同步练习】 4.2正弦
一、单选题
1.sin45°的值是( )
A. B. C. D.
2.已知,是锐角,则的度数为( )
A. B. C. D.
3. 在中,,,则的值为( )
A. B. C. D.
4.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )
A. B. C. D.
5.在平面直角坐标系中,从原点O引一条射线,设这条射线与x轴的正半轴的夹角为,若=,则这条射线是( )
A.OA B.OB C.OC D.OD
二、填空题
6.已知为锐角,,则= 度.
7.计算: .
8.中,,,则的值是 .
9.已知tanα= ,那么sinα= .(其中α为锐角)
10.cos60°= .
11.在Rt△ABC中,∠C=90°,a,b分别是∠A、∠B的对边,如果sinA:sinB=2:3,那么a:b等于 .
三、计算题
12.计算:
13.计算:4sin260°+tan45°-2sin30°
四、解答题
14.如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
15.计算: .
五、综合题
16.
(1)计算:cos30°- +(-1)0
(2)如图,在Rt△ABC中,∠A=30° ,BC=1,点D,E分别是直角边BC,AC的中点,求DE的长.
17.
(1)计算:
(2)如图,将矩形 绕点A顺时针旋转,得到矩形 ,点C的对应点 恰好落在 的延长线上,边 交边 于点E,求证:
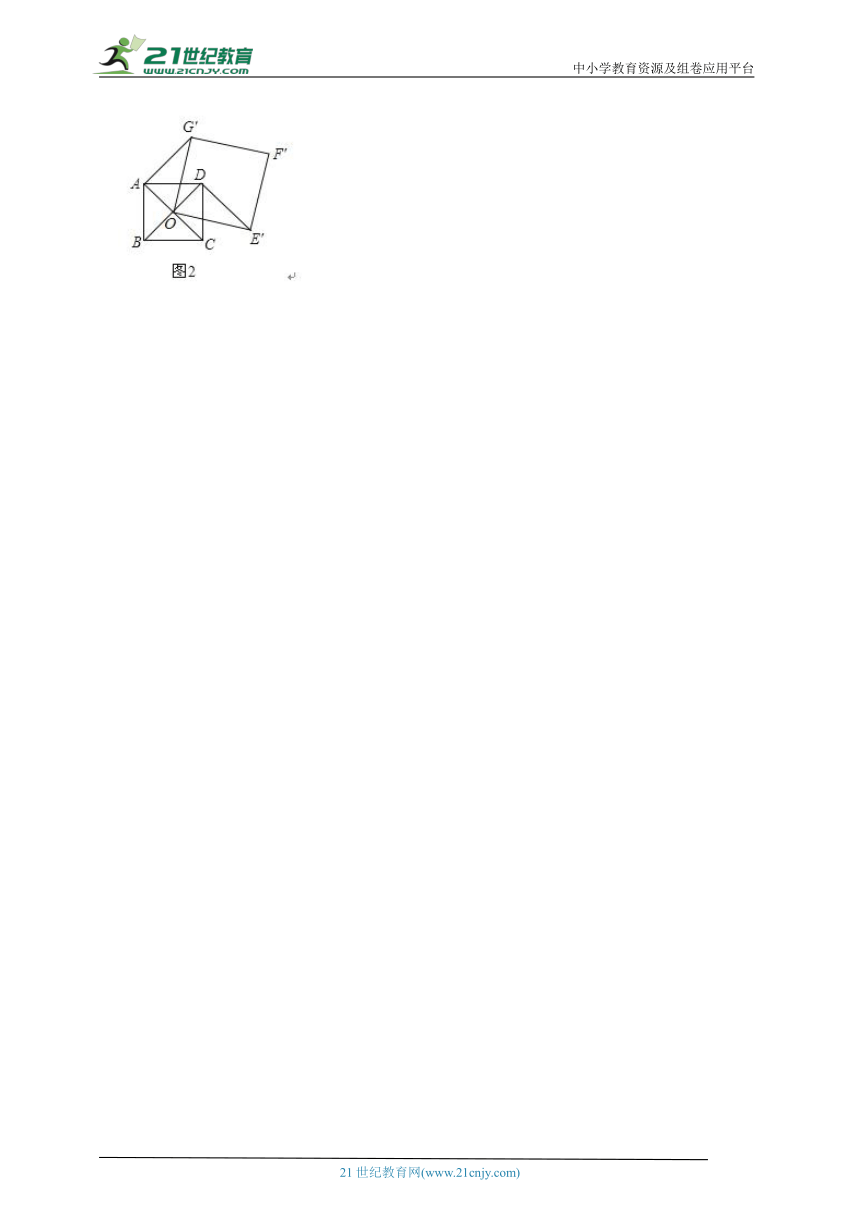
18.如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
答案解析部分
1.【答案】B
【知识点】求特殊角的三角函数值
2.【答案】B
【知识点】求特殊角的三角函数值
3.【答案】B
【知识点】锐角三角函数的定义;互余两角三角函数的关系
4.【答案】B
【知识点】锐角三角函数的定义
5.【答案】A
【知识点】勾股定理;锐角三角函数的定义
6.【答案】75
【知识点】求特殊角的三角函数值
7.【答案】
【知识点】零指数幂;负整数指数幂;求特殊角的三角函数值
8.【答案】
【知识点】勾股定理;锐角三角函数的定义
9.【答案】
【知识点】锐角三角函数的定义
10.【答案】0.5
【知识点】求特殊角的三角函数值
11.【答案】2:3
【知识点】互余两角三角函数的关系
12.【答案】
【知识点】零指数幂;求特殊角的三角函数值
13.【答案】解: 原式=4×()2+1-2×,
=3+1-1,
=3.
【知识点】求特殊角的三角函数值
14.【答案】解:Rt△ACD中,∵∠ADB=30°,AC=3米,∴AD=2AC=6(m)∵在Rt△ABC中,AB=AC÷sin58°≈3.53m,∴AD﹣AB=6﹣3.53≈2.5(m).∴调整后的滑梯AD比原滑梯AB增加2.5米
【知识点】含30°角的直角三角形;锐角三角函数的定义
15.【答案】解: ,
= ,
= .
【知识点】零指数幂;二次根式的混合运算;求特殊角的三角函数值
16.【答案】(1)解:cos30°- +(-1)0
;
(2)解:∵在Rt△ABC中,∠C=90°,∠A=30°,
∴AB=2BC=2.
又∵点D、E分别是BC,AC的中点,
∴DE是△ACB的中位线,
∴DE= AB=1.
【知识点】零指数幂;负整数指数幂;含30°角的直角三角形;求特殊角的三角函数值;三角形的中位线定理
17.【答案】(1)解:
;
(2)解:连结 、 ,如图,
∵四边形 为矩形,
∴ ,即 .
由旋转,得 ,
∴ .
【知识点】负整数指数幂;矩形的性质;求特殊角的三角函数值;旋转的性质
18.【答案】(1)解:如图1,延长ED交AG于点H,
∵点O是正方形ABCD两对角线的交点,
∴OA=OD,OA⊥OD,
∵OG=OE,
在△AOG和△DOE中,
,
∴△AOG≌△DOE,
∴∠AGO=∠DEO,
∵∠AGO+∠GAO=90°,
∴∠GAO+∠DEO=90°,
∴∠AHE=90°,
即DE⊥AG;
(2)解:
①在旋转过程中,∠OAG′成为直角有两种情况:
(Ⅰ)α由0°增大到90°过程中,当∠OAG′=90°时,
∵OA=OD=OG=OG′,
∴在Rt△OAG′中,sin∠AG′O==,
∴∠AG′O=30°,
∵OA⊥OD,OA⊥AG′,
∴OD∥AG′,
∴∠DOG′=∠AG′O=30°,
即α=30°;
(Ⅱ)α由90°增大到180°过程中,当∠OAG′=90°时,
同理可求∠BOG′=30°,
∴α=180°﹣30°=150°.
综上所述,当∠OAG′=90°时,α=30°或150°.
②如图3,当旋转到A、O、F′在一条直线上时,AF′的长最大,
∵正方形ABCD的边长为1,
∴OA=OD=OC=OB=,
∵OG=2OD,
∴OG′=OG=,
∴OF′=2,
∴AF′=AO+OF′=+2,
∵∠COE′=45°,
∴此时α=315°.
【知识点】一次函数的实际应用;全等三角形的判定与性质;正方形的性质;求特殊角的三角函数值
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【湘教版数学九年级上册同步练习】 4.2正弦
一、单选题
1.sin45°的值是( )
A. B. C. D.
2.已知,是锐角,则的度数为( )
A. B. C. D.
3. 在中,,,则的值为( )
A. B. C. D.
4.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )
A. B. C. D.
5.在平面直角坐标系中,从原点O引一条射线,设这条射线与x轴的正半轴的夹角为,若=,则这条射线是( )
A.OA B.OB C.OC D.OD
二、填空题
6.已知为锐角,,则= 度.
7.计算: .
8.中,,,则的值是 .
9.已知tanα= ,那么sinα= .(其中α为锐角)
10.cos60°= .
11.在Rt△ABC中,∠C=90°,a,b分别是∠A、∠B的对边,如果sinA:sinB=2:3,那么a:b等于 .
三、计算题
12.计算:
13.计算:4sin260°+tan45°-2sin30°
四、解答题
14.如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
15.计算: .
五、综合题
16.
(1)计算:cos30°- +(-1)0
(2)如图,在Rt△ABC中,∠A=30° ,BC=1,点D,E分别是直角边BC,AC的中点,求DE的长.
17.
(1)计算:
(2)如图,将矩形 绕点A顺时针旋转,得到矩形 ,点C的对应点 恰好落在 的延长线上,边 交边 于点E,求证:
18.如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
答案解析部分
1.【答案】B
【知识点】求特殊角的三角函数值
2.【答案】B
【知识点】求特殊角的三角函数值
3.【答案】B
【知识点】锐角三角函数的定义;互余两角三角函数的关系
4.【答案】B
【知识点】锐角三角函数的定义
5.【答案】A
【知识点】勾股定理;锐角三角函数的定义
6.【答案】75
【知识点】求特殊角的三角函数值
7.【答案】
【知识点】零指数幂;负整数指数幂;求特殊角的三角函数值
8.【答案】
【知识点】勾股定理;锐角三角函数的定义
9.【答案】
【知识点】锐角三角函数的定义
10.【答案】0.5
【知识点】求特殊角的三角函数值
11.【答案】2:3
【知识点】互余两角三角函数的关系
12.【答案】
【知识点】零指数幂;求特殊角的三角函数值
13.【答案】解: 原式=4×()2+1-2×,
=3+1-1,
=3.
【知识点】求特殊角的三角函数值
14.【答案】解:Rt△ACD中,∵∠ADB=30°,AC=3米,∴AD=2AC=6(m)∵在Rt△ABC中,AB=AC÷sin58°≈3.53m,∴AD﹣AB=6﹣3.53≈2.5(m).∴调整后的滑梯AD比原滑梯AB增加2.5米
【知识点】含30°角的直角三角形;锐角三角函数的定义
15.【答案】解: ,
= ,
= .
【知识点】零指数幂;二次根式的混合运算;求特殊角的三角函数值
16.【答案】(1)解:cos30°- +(-1)0
;
(2)解:∵在Rt△ABC中,∠C=90°,∠A=30°,
∴AB=2BC=2.
又∵点D、E分别是BC,AC的中点,
∴DE是△ACB的中位线,
∴DE= AB=1.
【知识点】零指数幂;负整数指数幂;含30°角的直角三角形;求特殊角的三角函数值;三角形的中位线定理
17.【答案】(1)解:
;
(2)解:连结 、 ,如图,
∵四边形 为矩形,
∴ ,即 .
由旋转,得 ,
∴ .
【知识点】负整数指数幂;矩形的性质;求特殊角的三角函数值;旋转的性质
18.【答案】(1)解:如图1,延长ED交AG于点H,
∵点O是正方形ABCD两对角线的交点,
∴OA=OD,OA⊥OD,
∵OG=OE,
在△AOG和△DOE中,
,
∴△AOG≌△DOE,
∴∠AGO=∠DEO,
∵∠AGO+∠GAO=90°,
∴∠GAO+∠DEO=90°,
∴∠AHE=90°,
即DE⊥AG;
(2)解:
①在旋转过程中,∠OAG′成为直角有两种情况:
(Ⅰ)α由0°增大到90°过程中,当∠OAG′=90°时,
∵OA=OD=OG=OG′,
∴在Rt△OAG′中,sin∠AG′O==,
∴∠AG′O=30°,
∵OA⊥OD,OA⊥AG′,
∴OD∥AG′,
∴∠DOG′=∠AG′O=30°,
即α=30°;
(Ⅱ)α由90°增大到180°过程中,当∠OAG′=90°时,
同理可求∠BOG′=30°,
∴α=180°﹣30°=150°.
综上所述,当∠OAG′=90°时,α=30°或150°.
②如图3,当旋转到A、O、F′在一条直线上时,AF′的长最大,
∵正方形ABCD的边长为1,
∴OA=OD=OC=OB=,
∵OG=2OD,
∴OG′=OG=,
∴OF′=2,
∴AF′=AO+OF′=+2,
∵∠COE′=45°,
∴此时α=315°.
【知识点】一次函数的实际应用;全等三角形的判定与性质;正方形的性质;求特殊角的三角函数值
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
