【湘教版数学九年级上册同步练习】 4.3解直角三角形(含答案)
文档属性
| 名称 | 【湘教版数学九年级上册同步练习】 4.3解直角三角形(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【湘教版数学九年级上册同步练习】
4.3解直角三角形
一、单选题
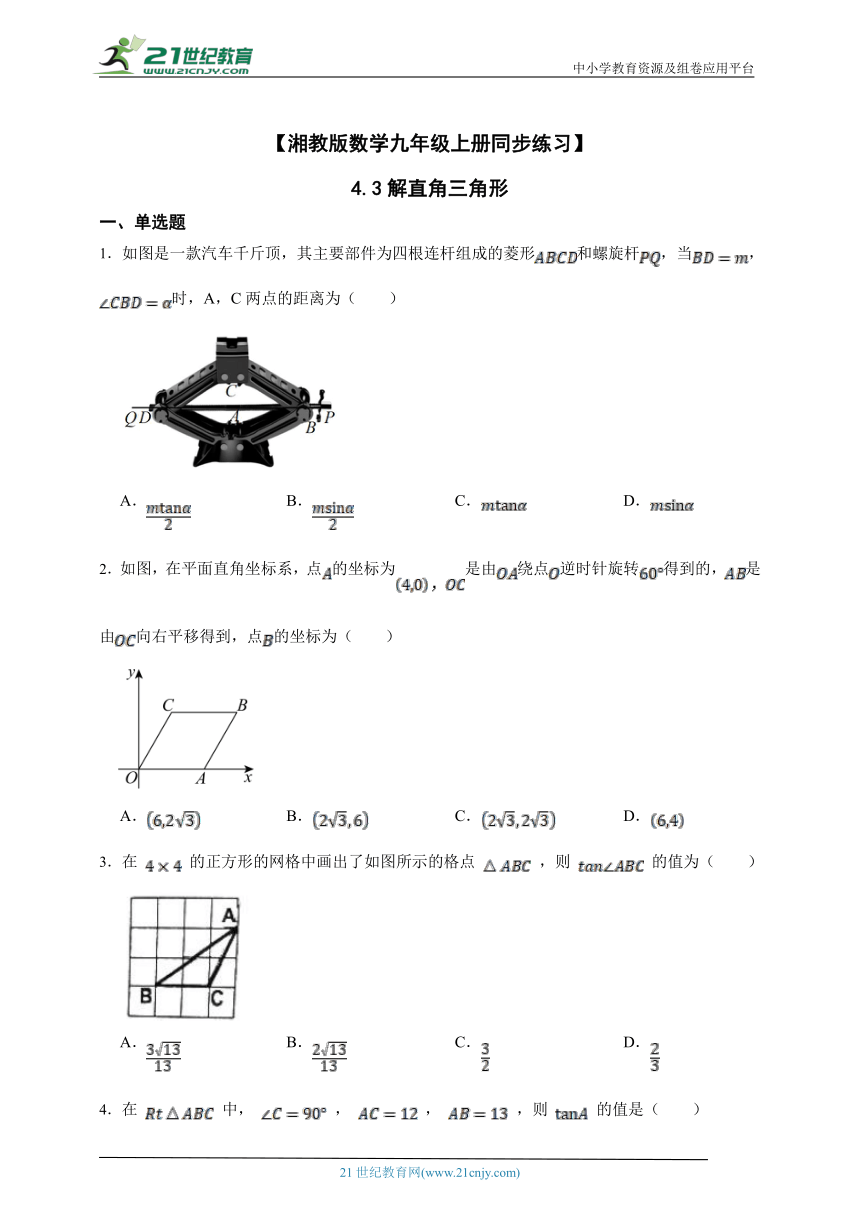
1.如图是一款汽车千斤顶,其主要部件为四根连杆组成的菱形和螺旋杆,当,时,A,C两点的距离为( )
A. B. C. D.
2.如图,在平面直角坐标系,点的坐标为是由绕点逆时针旋转得到的,是由向右平移得到,点的坐标为( )
A. B. C. D.
3.在 的正方形的网格中画出了如图所示的格点 ,则 的值为( )
A. B. C. D.
4.在 中, , , ,则 的值是( )
A. B. C. D.
5.在中,,若,,则的长是( )
A.80 B. C.60 D.
二、填空题
6.如图,在中,,,点C 关于直线的对称点为D,E为边上不与点A,C重合的动点,连接,过点D作的垂线交于点F,则的值为 .
7.如图,AB是⊙O的直径,AB=13,AC=5,则tan∠ADC= .
8.在△ABC中,∠C=90°,如果tan∠A=2,AC=3,那么BC= .
9.如图,在矩形中,对角线与相交于点O,,,垂足为点E,F是的中点,连接,若,则矩形的周长是 .
10.如图,在平面直角坐标系中,等边三角形OAB的边OB在x轴上,点A在第一象限,,点C在线段OA上,且.将沿射线OA的方向平移至的位置,此时点的坐标是 .
11.在平面直角坐标系中,为等边三角形,点的坐标为,把按如图所示的方式放置,并将进行变换:第一次变换将绕着原点顺时针旋转,同时边长扩大为边长的倍,得到第二次变换将绕着原点顺时针旋转,同时边长扩大为边长的倍,得到,……,依此类推,得到,则点的坐标为 .
三、计算题
12.如图,在中,,,,求的长.
13.阅读理解:通过学习三角函数,我们知道在直角三角形中,一个锐角的大小,与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似地,可以在等腰三角形中,建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角正对().如图(1),在中,,顶角的正对记作“”,这时底边腰.容易知道一个角的大小,与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
(1)如图(2),利用等腰直角三角形计算:______;
(2)如图(3),在等腰中,,若,求的值.
四、解答题
14. 如图,在Rt△ABC中, ,D是AB的中点,过D点作AB的垂线交AC于点E,若BC=6,sinA= ,求DE的长.
15.如图,在中,,,,求和的长.
五、综合题
16.如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
(1)求∠ACD度数;
(2)当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)
17.如图①,将直尺摆放在三角板上,使直尺与三角板的边分别交于点D、E、F、G,∠CGD=42°.将直尺向下平移,使直尺的边缘通过点B,交AC于点H,如图②所示。
【参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90】
(1)∠CBH的大小为 度.
(2)点H、B的读数分别为4、13.4,求BC的长.(结果精确到0.01)
18.在△ABC中,∠C=90°.
(1)已知c=8,∠A=60°,求∠B,a,b;
(2)已知a=3,∠A=45°,求∠B,b,c.
答案解析部分
1.【答案】C
【知识点】菱形的性质;解直角三角形
2.【答案】A
【知识点】坐标与图形性质;解直角三角形;旋转的性质
3.【答案】D
【知识点】解直角三角形
4.【答案】B
【知识点】解直角三角形
5.【答案】A
【知识点】勾股定理;解直角三角形
6.【答案】
【知识点】相似三角形的判定与性质;解直角三角形
7.【答案】
【知识点】解直角三角形
8.【答案】
【知识点】解直角三角形
9.【答案】
【知识点】矩形的性质;解直角三角形;三角形的中位线定理
10.【答案】(,)
【知识点】平移的性质;解直角三角形
11.【答案】
【知识点】等边三角形的判定与性质;解直角三角形;坐标与图形变化﹣旋转
12.【答案】
【知识点】解直角三角形
13.【答案】(1)
(2).
【知识点】勾股定理;解直角三角形
14.【答案】解:∵BC=6,sinA= , ∴AB=10, ∴AC= =8, ∵D是AB的中点, ∴AD= AB=5, ∵∠ADE=∠C=90°, ∠A=∠A ∴△ADE∽△ACB, ∴ = ,即 = , 解得:DE= .
【知识点】相似三角形的判定与性质;解直角三角形
15.【答案】,
【知识点】含30°角的直角三角形;勾股定理;解直角三角形
16.【答案】(1)解:延长AC交ON于点E,如图,
∵AC⊥ON,
∴∠OEC=90°,
在Rt△OEC中,
∵∠O=25°,
∴∠OCE=65°,
∴∠ACB=∠OCE=65°,
∴∠ACD=90°﹣∠ACB=25°
(2)解:∵四边形ABCD是矩形,
∴∠ABC=90°,AD=BC,
在Rt△ABC中,∵cos∠ACB= ,
∴BC=AC cos65°=5×0.42=2.1,
∴AD=BC=2.1
【知识点】解直角三角形
17.【答案】(1)42
(2)解:由图得,BH=13.4-4=9.4.
在Rt△BCH中,∠C=90°,∠CBH=42°,
∵ , ∴ . ∴BC的长约为6.96
【知识点】平移的性质;解直角三角形
18.【答案】(1)解:△ABC中,∠C=90°,∠A=60°,
,
c=8,
,
(2)解:
△ABC中,∠C=90°,∠A=45°,
,
a=3
,
【知识点】解直角三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【湘教版数学九年级上册同步练习】
4.3解直角三角形
一、单选题
1.如图是一款汽车千斤顶,其主要部件为四根连杆组成的菱形和螺旋杆,当,时,A,C两点的距离为( )
A. B. C. D.
2.如图,在平面直角坐标系,点的坐标为是由绕点逆时针旋转得到的,是由向右平移得到,点的坐标为( )
A. B. C. D.
3.在 的正方形的网格中画出了如图所示的格点 ,则 的值为( )
A. B. C. D.
4.在 中, , , ,则 的值是( )
A. B. C. D.
5.在中,,若,,则的长是( )
A.80 B. C.60 D.
二、填空题
6.如图,在中,,,点C 关于直线的对称点为D,E为边上不与点A,C重合的动点,连接,过点D作的垂线交于点F,则的值为 .
7.如图,AB是⊙O的直径,AB=13,AC=5,则tan∠ADC= .
8.在△ABC中,∠C=90°,如果tan∠A=2,AC=3,那么BC= .
9.如图,在矩形中,对角线与相交于点O,,,垂足为点E,F是的中点,连接,若,则矩形的周长是 .
10.如图,在平面直角坐标系中,等边三角形OAB的边OB在x轴上,点A在第一象限,,点C在线段OA上,且.将沿射线OA的方向平移至的位置,此时点的坐标是 .
11.在平面直角坐标系中,为等边三角形,点的坐标为,把按如图所示的方式放置,并将进行变换:第一次变换将绕着原点顺时针旋转,同时边长扩大为边长的倍,得到第二次变换将绕着原点顺时针旋转,同时边长扩大为边长的倍,得到,……,依此类推,得到,则点的坐标为 .
三、计算题
12.如图,在中,,,,求的长.
13.阅读理解:通过学习三角函数,我们知道在直角三角形中,一个锐角的大小,与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似地,可以在等腰三角形中,建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角正对().如图(1),在中,,顶角的正对记作“”,这时底边腰.容易知道一个角的大小,与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
(1)如图(2),利用等腰直角三角形计算:______;
(2)如图(3),在等腰中,,若,求的值.
四、解答题
14. 如图,在Rt△ABC中, ,D是AB的中点,过D点作AB的垂线交AC于点E,若BC=6,sinA= ,求DE的长.
15.如图,在中,,,,求和的长.
五、综合题
16.如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
(1)求∠ACD度数;
(2)当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)
17.如图①,将直尺摆放在三角板上,使直尺与三角板的边分别交于点D、E、F、G,∠CGD=42°.将直尺向下平移,使直尺的边缘通过点B,交AC于点H,如图②所示。
【参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90】
(1)∠CBH的大小为 度.
(2)点H、B的读数分别为4、13.4,求BC的长.(结果精确到0.01)
18.在△ABC中,∠C=90°.
(1)已知c=8,∠A=60°,求∠B,a,b;
(2)已知a=3,∠A=45°,求∠B,b,c.
答案解析部分
1.【答案】C
【知识点】菱形的性质;解直角三角形
2.【答案】A
【知识点】坐标与图形性质;解直角三角形;旋转的性质
3.【答案】D
【知识点】解直角三角形
4.【答案】B
【知识点】解直角三角形
5.【答案】A
【知识点】勾股定理;解直角三角形
6.【答案】
【知识点】相似三角形的判定与性质;解直角三角形
7.【答案】
【知识点】解直角三角形
8.【答案】
【知识点】解直角三角形
9.【答案】
【知识点】矩形的性质;解直角三角形;三角形的中位线定理
10.【答案】(,)
【知识点】平移的性质;解直角三角形
11.【答案】
【知识点】等边三角形的判定与性质;解直角三角形;坐标与图形变化﹣旋转
12.【答案】
【知识点】解直角三角形
13.【答案】(1)
(2).
【知识点】勾股定理;解直角三角形
14.【答案】解:∵BC=6,sinA= , ∴AB=10, ∴AC= =8, ∵D是AB的中点, ∴AD= AB=5, ∵∠ADE=∠C=90°, ∠A=∠A ∴△ADE∽△ACB, ∴ = ,即 = , 解得:DE= .
【知识点】相似三角形的判定与性质;解直角三角形
15.【答案】,
【知识点】含30°角的直角三角形;勾股定理;解直角三角形
16.【答案】(1)解:延长AC交ON于点E,如图,
∵AC⊥ON,
∴∠OEC=90°,
在Rt△OEC中,
∵∠O=25°,
∴∠OCE=65°,
∴∠ACB=∠OCE=65°,
∴∠ACD=90°﹣∠ACB=25°
(2)解:∵四边形ABCD是矩形,
∴∠ABC=90°,AD=BC,
在Rt△ABC中,∵cos∠ACB= ,
∴BC=AC cos65°=5×0.42=2.1,
∴AD=BC=2.1
【知识点】解直角三角形
17.【答案】(1)42
(2)解:由图得,BH=13.4-4=9.4.
在Rt△BCH中,∠C=90°,∠CBH=42°,
∵ , ∴ . ∴BC的长约为6.96
【知识点】平移的性质;解直角三角形
18.【答案】(1)解:△ABC中,∠C=90°,∠A=60°,
,
c=8,
,
(2)解:
△ABC中,∠C=90°,∠A=45°,
,
a=3
,
【知识点】解直角三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
