广东省惠州市2023-2024学年高一数学下学期期末测试卷(PDF版无答案)
文档属性
| 名称 | 广东省惠州市2023-2024学年高一数学下学期期末测试卷(PDF版无答案) |

|
|
| 格式 | |||
| 文件大小 | 371.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 00:00:00 | ||
图片预览


文档简介
惠州市 2023-2024 学年第二学期期末质量检测试题
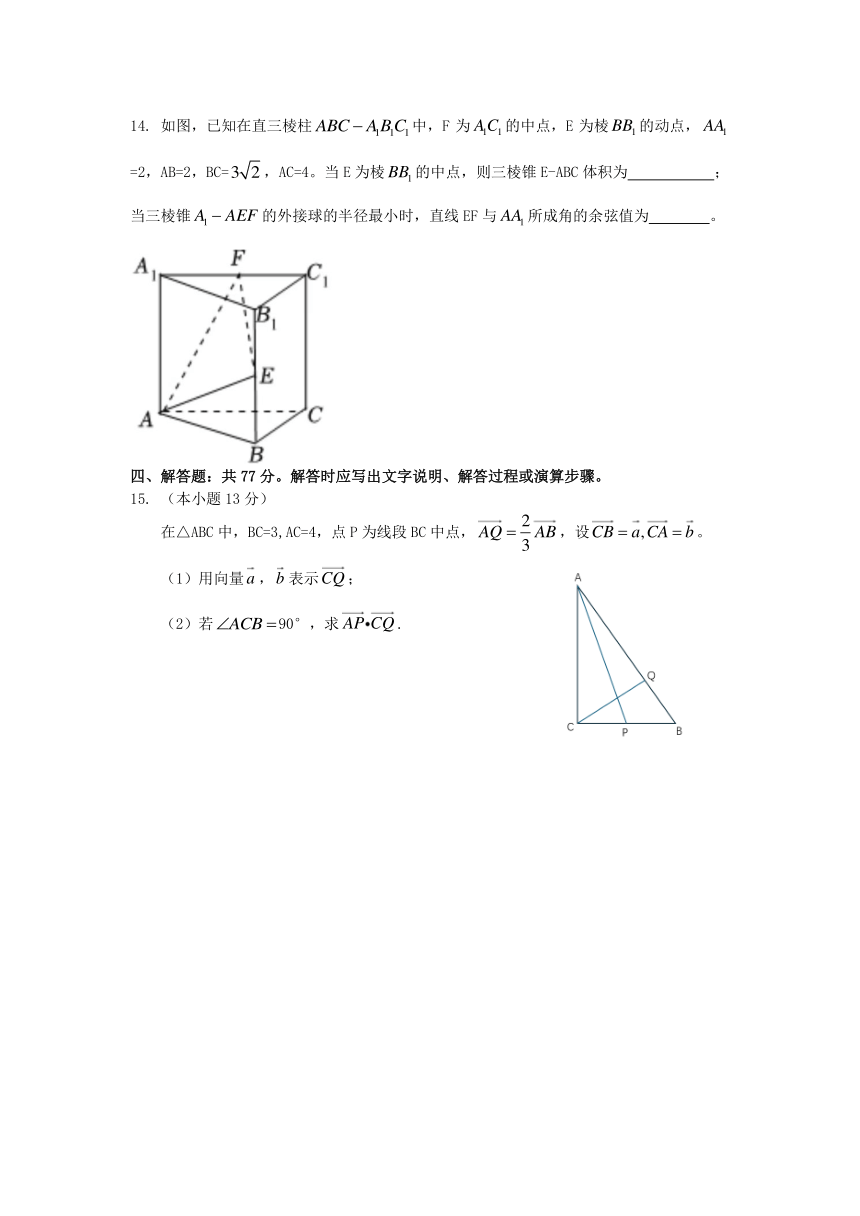
高一数学
全卷满分 150 分,时间 120 分钟。
注意事项:
1. 答题前,考生务必将自己的姓名、准考证号、座位号、学校、班级等考生信息填写
在答题卡上。
2. 作答单项及多项选择题时,选出每个小题答案后,用 2B 铅笔把答题卡上对应题目
的答案信息点涂黑。如需改动,用橡皮擦干净后,再选涂其它答案,写在本试卷上无效。
3. 非选择题必须用黑色字迹签字笔作答,答案必须写在答题卡各题指定的位置上,写
在本试卷上无效。
一、 单选题:本大题共 8小题,每小题 5分,共 40 分。在每个小题给出的四个选项中,只
有一项是符合题目要求,选对得 5 分,选错得 0分。
2 3i
1. 在复平面内,复数 对应的点的坐标在( )
1+ i
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2. 下列命题中正确的是( )
A.零向量没有方向 B.共线向量一定是相等向量
C.若 为实数,则向量 a 与 a 方向相同 D.单位向量的模都相等
3. 已 知 数 据 x , x , x , x 的 平 数 数 为 10 , 方 差 为 10 , 则1 2 3 8
3x1 +2,3x +2,3x +2, 3x +2的平数数和方差分别为( ) 2 3 8
A.32,90 B.32,92 C.30,90 D.30,92
4. 已知向量a = (1, 2 ),b = (2,0),则向量 a 在b 方向上的投影向量为( )
A.(1,2) B.(2,0) C.(1,0) D.(2,1)
5. 某校有小学生、初中生和高中生,其人数比是 5:4:3,为了了解该校学生的视力情况,
采用按比例分层抽样的方法抽取一个样本量为 n 的样本,已知样本中高中生的人数比小学
生的人数少 20,则 n=( )
A.100 B.120 C.200 D.240
6. 设 , 是两个不重合的平面,m,n是两条直线,则下列命题为真命题的是( )
A.若 m ,n ,m⊥n,则 ⊥ B.若 m∥ ,n ,则 m∥n
C.若 m ,n ,m∥ ,n∥ ,则 D.若 m⊥ ,n ,则 m⊥n
7. 掷两颗骰子,观察掷得的点数。设事件 A表示“两个点数都是偶数”,事件 B表示“两
个点数都是奇数”,事件 C表示“两个点数之和是偶数”,事件 D表示“两个点数的乘积是偶
数”。那么下列结论正确的是( )
A.A 与 B 是对立事件 B.A 与C D是互斥事件
C.B 与 D 是相互独立事件 D.B 与C D是相互独立事件
8. 已知直三棱柱 ABC- A1B1C1 的积积为 8,二面角C1 AB C 的大小为
,且 AC=BC,CC =2,则点 A1到平面 ABC 的距离为( ) 1 1
4
2 2 2
A. 2 B. C. D.
2 3 4
二、多选题:本大题共 3小题,每小题 6分,共 18 分。在每个小题给出的四个选项中,有
多项是符合题目要求的。全部选对的得 6分,有选错的得 0分,部分选对的得部分分。
9. 如图,一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径 2R 相等,下列结
论正确的是( )
2
A.圆柱的侧面积为4 R
2
B. 圆柱的侧面积为 5 R
C.圆柱的侧面积与球的表面积相等
D.三个几何积的表面积中,球的表面积最小
10. 设 z为复数(i为虚数单位),下列命题正确的有( )
A.若(1+i)z=-i,则|z|=1
B.对任意复数 z1, z ,有2 | z1z2 |=| z1 | | z 2 |
C.对任意复数 z , z ,有 z1 z2 = z1 z1 2 2
D.在复平面内,若 M= z || z 2 | 2 ,则集合 M所构成区域的面积为 6π
11. 在△ABC 中,角 A,B,C所对的边分别是 a,b,c,下列命题正确的是( )
A.若 A=60°,a=2,则△ABC 面积的最大值为 3
B.若 A=60°,a=1,则△ABC 面积的最大值为 3
C.若 a=2 3 ,b=4,要使满足条件的三角形有且只有两个,则 A ,
6 3
3 2 2
D.若 a+b=c(cosA+cosB),且 c=1,则该三角形内切圆面积的最大值是
4
三、填空题:(本大题共 3小题,每题 5分,共计 15分)
2 3
12. 甲、乙两人独立的解同一道题,甲、乙解对题的概率分别是 、 ,那么恰好只有 1人
3 5
解对题的概率是 。
13. 已知频率分布直方图如右图所示,记其平数数为 a,中位数为 b,则 a
与 b的大小关系为 。
14. 如图,已知在直三棱柱 ABC A BC 中,F 为 A1C1 的中点,E 为棱BB1 的动点, AA1 1 1 1
=2,AB=2,BC=3 2 ,AC=4。当 E为棱BB1 的中点,则三棱锥 E-ABC 积积为 ;
当三棱锥 A1 AEF 的外接球的半径最小时,直线 EF 与 AA1 所成角的余弦值为 。
四、解答题:共 77 分。解答时应写出文字说明、解答过程或演算步骤。
15. (本小题 13 分)
2
在△ABC 中,BC=3,AC=4,点 P为线段 BC中点, AQ = AB,设CB = a,CA = b。
3
(1)用向量 a ,b 表示CQ;
(2)若 ACB =90°,求 AP CQ .
16. (本小题 15 分)
已知有下面三个条件:
3 a cos A+1 sin B sinC sin2 A
① S = (AC AB) ; ② = ; ③ + = +1
2 c 3 sin C sinC sin B sin B sinC
请从这三个条件中任选一个,补充在下面的横线上,并解答问题:
在△ABC 中,角 A,B,C所对的边分别是 a,b,c,且 。
(1)求角 A的大小;
(2)若 AD 是△ABC 的角平分线,且 b=2,c=3,求线段 AD 的长。
17. (本小题 15 分)
为了研究学生每天总结整理数学错题情况,某课题组在我市中学生中随机抽取了 100 名
学生调查了他们期中考试的数学成绩和平时总结整理数学错题情况,并绘制了下列两个统计
图表,图 1为学生期中考试数学成绩的频率分布直方图,图 2为学生一个星期内总结整理数
学错题天数的扇形图。若本次数学成绩在 110 分及以上视为优秀,将一个星期有 4天及以上
总结整理数学错题视为“经常总结整理”,少于 4天视为“不经常总结整理”。已知数学成绩
优秀的学生中,经常总结整理错题的学生占 70%。
数学成绩优秀 数学成绩不优秀 合计
经常整理
不经常总结整理
合计
(1)根据图 1、图 2的数据,补全表格;
(2)求图 1中 m的值及学生期中考试数学成绩的第 65 百分位数;
(3)抽取的 100 名学生中按“经常总结整理错题”与“不经常总结整理错题”进行分
层抽样,随机抽取 5名学生,再从这 5名学生中随机抽取 2人进行座谈,求这 2名同学
数来自“经常总结整理错题”的概率。
18. (本小题 17 分)
如图,在四棱锥 Q-ABCD 中,底面 ABCD 是正方形,侧面 QAD 是正三角形,面 QAD⊥面
ABCD,M 是 QD 的中点。
(1)求证:BQ∥平面 AMC;
(2)求直线 AC与平面 QCD 所成角的正弦值;
QN
(3)在棱 QC 上是否存在点 N 使平面 BDN⊥平面 AMC 成立?如果存在,求出 ,如果
NC
不存在,说明理由。
19. (本小题 17 分)
将连续正整数 1,2,…,n (n N )从小到大排列构成一个数 123…n,F( n)为这个数
的位数(如当 n=12 时,此数为 123456789101112,共有 15个数字,F( 12)=15),现从这个
数中随机取一个数字,恰好取到 0的概率记为 p(n)。
(1)求 p(100);
(2)当 n≤2021 时,求 F(n)的表达式;
(3)令 g( n)为这个数中数字 0的个数,f( n)为这个数中数字 9的个数,h( n)=f
(n)-g(n), S = n | h (n) =1,n 100,n N ,求当n S 时,p(n)的最大值。
高一数学
全卷满分 150 分,时间 120 分钟。
注意事项:
1. 答题前,考生务必将自己的姓名、准考证号、座位号、学校、班级等考生信息填写
在答题卡上。
2. 作答单项及多项选择题时,选出每个小题答案后,用 2B 铅笔把答题卡上对应题目
的答案信息点涂黑。如需改动,用橡皮擦干净后,再选涂其它答案,写在本试卷上无效。
3. 非选择题必须用黑色字迹签字笔作答,答案必须写在答题卡各题指定的位置上,写
在本试卷上无效。
一、 单选题:本大题共 8小题,每小题 5分,共 40 分。在每个小题给出的四个选项中,只
有一项是符合题目要求,选对得 5 分,选错得 0分。
2 3i
1. 在复平面内,复数 对应的点的坐标在( )
1+ i
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2. 下列命题中正确的是( )
A.零向量没有方向 B.共线向量一定是相等向量
C.若 为实数,则向量 a 与 a 方向相同 D.单位向量的模都相等
3. 已 知 数 据 x , x , x , x 的 平 数 数 为 10 , 方 差 为 10 , 则1 2 3 8
3x1 +2,3x +2,3x +2, 3x +2的平数数和方差分别为( ) 2 3 8
A.32,90 B.32,92 C.30,90 D.30,92
4. 已知向量a = (1, 2 ),b = (2,0),则向量 a 在b 方向上的投影向量为( )
A.(1,2) B.(2,0) C.(1,0) D.(2,1)
5. 某校有小学生、初中生和高中生,其人数比是 5:4:3,为了了解该校学生的视力情况,
采用按比例分层抽样的方法抽取一个样本量为 n 的样本,已知样本中高中生的人数比小学
生的人数少 20,则 n=( )
A.100 B.120 C.200 D.240
6. 设 , 是两个不重合的平面,m,n是两条直线,则下列命题为真命题的是( )
A.若 m ,n ,m⊥n,则 ⊥ B.若 m∥ ,n ,则 m∥n
C.若 m ,n ,m∥ ,n∥ ,则 D.若 m⊥ ,n ,则 m⊥n
7. 掷两颗骰子,观察掷得的点数。设事件 A表示“两个点数都是偶数”,事件 B表示“两
个点数都是奇数”,事件 C表示“两个点数之和是偶数”,事件 D表示“两个点数的乘积是偶
数”。那么下列结论正确的是( )
A.A 与 B 是对立事件 B.A 与C D是互斥事件
C.B 与 D 是相互独立事件 D.B 与C D是相互独立事件
8. 已知直三棱柱 ABC- A1B1C1 的积积为 8,二面角C1 AB C 的大小为
,且 AC=BC,CC =2,则点 A1到平面 ABC 的距离为( ) 1 1
4
2 2 2
A. 2 B. C. D.
2 3 4
二、多选题:本大题共 3小题,每小题 6分,共 18 分。在每个小题给出的四个选项中,有
多项是符合题目要求的。全部选对的得 6分,有选错的得 0分,部分选对的得部分分。
9. 如图,一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径 2R 相等,下列结
论正确的是( )
2
A.圆柱的侧面积为4 R
2
B. 圆柱的侧面积为 5 R
C.圆柱的侧面积与球的表面积相等
D.三个几何积的表面积中,球的表面积最小
10. 设 z为复数(i为虚数单位),下列命题正确的有( )
A.若(1+i)z=-i,则|z|=1
B.对任意复数 z1, z ,有2 | z1z2 |=| z1 | | z 2 |
C.对任意复数 z , z ,有 z1 z2 = z1 z1 2 2
D.在复平面内,若 M= z || z 2 | 2 ,则集合 M所构成区域的面积为 6π
11. 在△ABC 中,角 A,B,C所对的边分别是 a,b,c,下列命题正确的是( )
A.若 A=60°,a=2,则△ABC 面积的最大值为 3
B.若 A=60°,a=1,则△ABC 面积的最大值为 3
C.若 a=2 3 ,b=4,要使满足条件的三角形有且只有两个,则 A ,
6 3
3 2 2
D.若 a+b=c(cosA+cosB),且 c=1,则该三角形内切圆面积的最大值是
4
三、填空题:(本大题共 3小题,每题 5分,共计 15分)
2 3
12. 甲、乙两人独立的解同一道题,甲、乙解对题的概率分别是 、 ,那么恰好只有 1人
3 5
解对题的概率是 。
13. 已知频率分布直方图如右图所示,记其平数数为 a,中位数为 b,则 a
与 b的大小关系为 。
14. 如图,已知在直三棱柱 ABC A BC 中,F 为 A1C1 的中点,E 为棱BB1 的动点, AA1 1 1 1
=2,AB=2,BC=3 2 ,AC=4。当 E为棱BB1 的中点,则三棱锥 E-ABC 积积为 ;
当三棱锥 A1 AEF 的外接球的半径最小时,直线 EF 与 AA1 所成角的余弦值为 。
四、解答题:共 77 分。解答时应写出文字说明、解答过程或演算步骤。
15. (本小题 13 分)
2
在△ABC 中,BC=3,AC=4,点 P为线段 BC中点, AQ = AB,设CB = a,CA = b。
3
(1)用向量 a ,b 表示CQ;
(2)若 ACB =90°,求 AP CQ .
16. (本小题 15 分)
已知有下面三个条件:
3 a cos A+1 sin B sinC sin2 A
① S = (AC AB) ; ② = ; ③ + = +1
2 c 3 sin C sinC sin B sin B sinC
请从这三个条件中任选一个,补充在下面的横线上,并解答问题:
在△ABC 中,角 A,B,C所对的边分别是 a,b,c,且 。
(1)求角 A的大小;
(2)若 AD 是△ABC 的角平分线,且 b=2,c=3,求线段 AD 的长。
17. (本小题 15 分)
为了研究学生每天总结整理数学错题情况,某课题组在我市中学生中随机抽取了 100 名
学生调查了他们期中考试的数学成绩和平时总结整理数学错题情况,并绘制了下列两个统计
图表,图 1为学生期中考试数学成绩的频率分布直方图,图 2为学生一个星期内总结整理数
学错题天数的扇形图。若本次数学成绩在 110 分及以上视为优秀,将一个星期有 4天及以上
总结整理数学错题视为“经常总结整理”,少于 4天视为“不经常总结整理”。已知数学成绩
优秀的学生中,经常总结整理错题的学生占 70%。
数学成绩优秀 数学成绩不优秀 合计
经常整理
不经常总结整理
合计
(1)根据图 1、图 2的数据,补全表格;
(2)求图 1中 m的值及学生期中考试数学成绩的第 65 百分位数;
(3)抽取的 100 名学生中按“经常总结整理错题”与“不经常总结整理错题”进行分
层抽样,随机抽取 5名学生,再从这 5名学生中随机抽取 2人进行座谈,求这 2名同学
数来自“经常总结整理错题”的概率。
18. (本小题 17 分)
如图,在四棱锥 Q-ABCD 中,底面 ABCD 是正方形,侧面 QAD 是正三角形,面 QAD⊥面
ABCD,M 是 QD 的中点。
(1)求证:BQ∥平面 AMC;
(2)求直线 AC与平面 QCD 所成角的正弦值;
QN
(3)在棱 QC 上是否存在点 N 使平面 BDN⊥平面 AMC 成立?如果存在,求出 ,如果
NC
不存在,说明理由。
19. (本小题 17 分)
将连续正整数 1,2,…,n (n N )从小到大排列构成一个数 123…n,F( n)为这个数
的位数(如当 n=12 时,此数为 123456789101112,共有 15个数字,F( 12)=15),现从这个
数中随机取一个数字,恰好取到 0的概率记为 p(n)。
(1)求 p(100);
(2)当 n≤2021 时,求 F(n)的表达式;
(3)令 g( n)为这个数中数字 0的个数,f( n)为这个数中数字 9的个数,h( n)=f
(n)-g(n), S = n | h (n) =1,n 100,n N ,求当n S 时,p(n)的最大值。
同课章节目录
