九年级数学(华师大版)下册教学课件:26.3 二次函数实践与探索(共19张PPT)
文档属性
| 名称 | 九年级数学(华师大版)下册教学课件:26.3 二次函数实践与探索(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 285.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-26 21:59:13 | ||
图片预览



文档简介
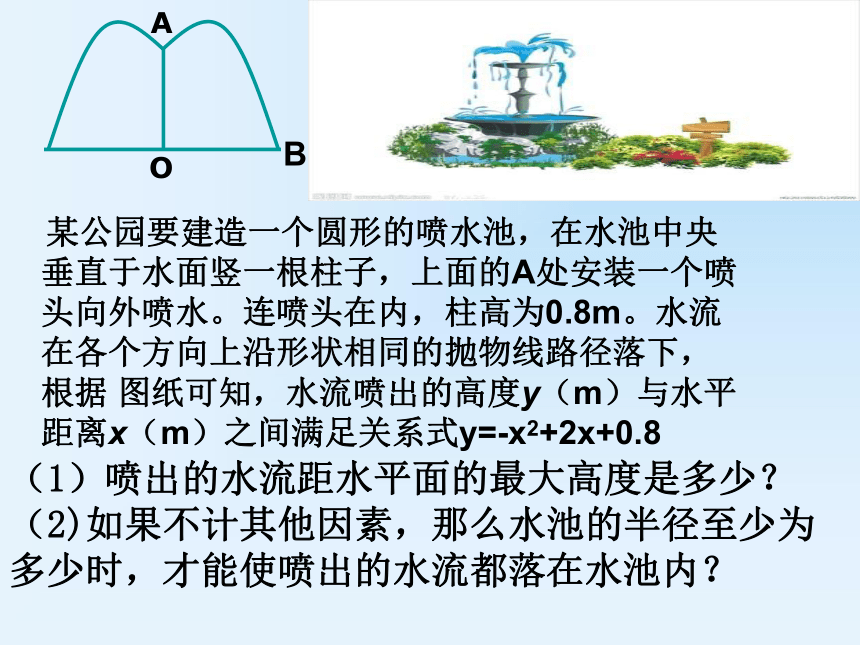
课件19张PPT。《二次函数实践与探索》 某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水。连喷头在内,柱高为0.8m。水流在各个方向上沿形状相同的抛物线路径落下,根据 图纸可知,水流喷出的高度y(m)与水平距离x(m)之间满足关系式y=-x2+2x+0.8
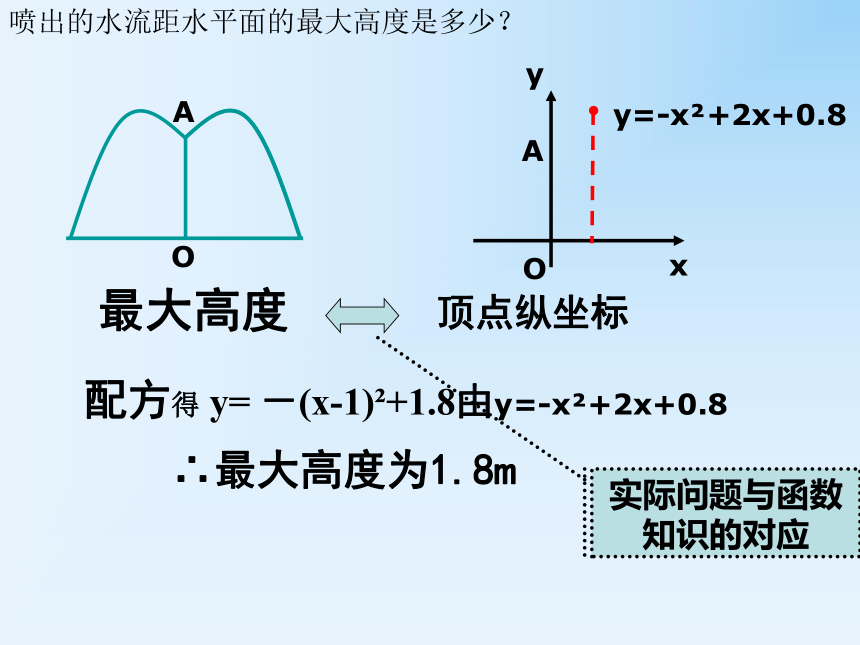
(1)喷出的水流距水平面的最大高度是多少?
(2)如果不计其他因素,那么水池的半径至少为 多少时,才能使喷出的水流都落在水池内?By=-x2+2x+0.8最大高度顶点纵坐标实际问题与函数知识的对应配方得 y= -(x-1)2+1.8由y=-x2+2x+0.8∴最大高度为1.8m喷出的水流距水平面的最大高度是多少?yx水池的半径至少为多少时,才能使喷出的水流都落在水池内?
析题分意:水池为圆形,O点在中央,喷水的落点到圆心的距离相等。最小半径线段OB的长度
(B点的横坐标)∴最小半径为2.34m注意自变量的实际意义BC令y=0,即-(x-1)2+1.8 =0
则x的值为 x1≈2.34 x2≈– 0.34舍去水池的半径至少为多少时,才能使喷出的水流都落在水池内?( 2.236,结果保留两位小数)
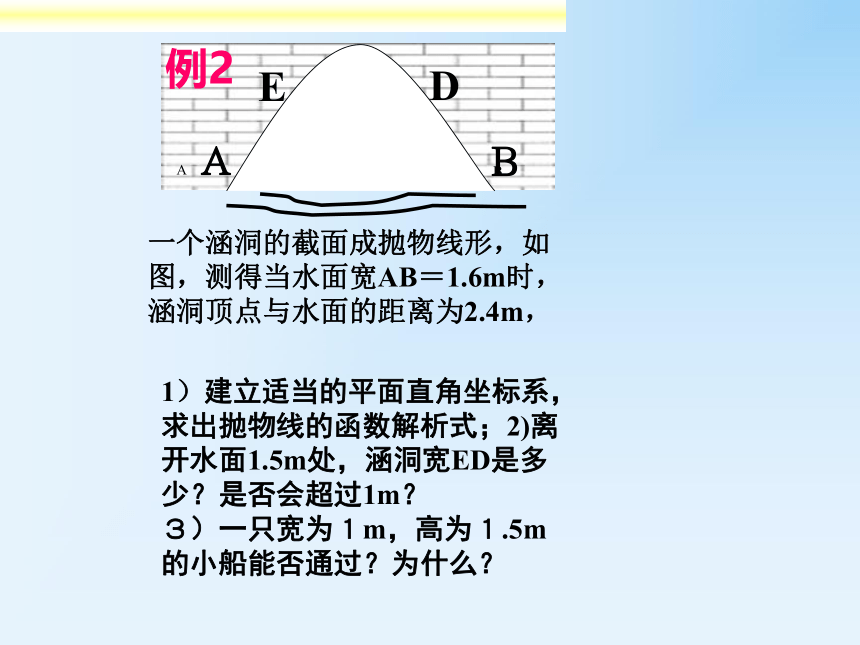
(不合题意,舍去)y=-x2+2x+0.8一个涵洞的截面成抛物线形,如图,测得当水面宽AB=1.6m时,涵洞顶点与水面的距离为2.4m,1)建立适当的平面直角坐标系,求出抛物线的函数解析式;2)离开水面1.5m处,涵洞宽ED是多少?是否会超过1m?
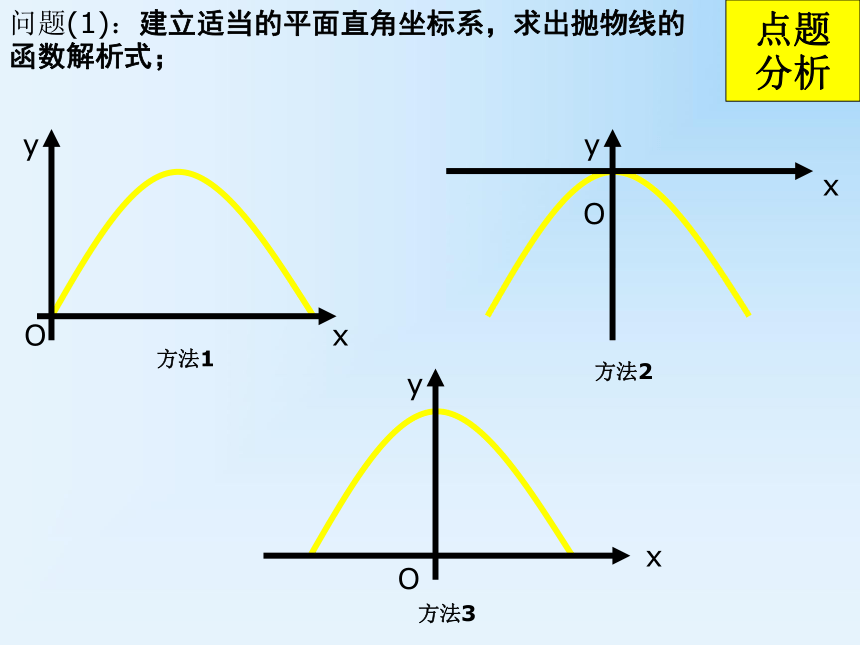
3)一只宽为1m,高为1.5m的小船能否通过?为什么?例2点题 分析问题(1):建立适当的平面直角坐标系,求出抛物线的函数解析式;yxO方法1方法2方法3y=- x2+2.4点题 分析问题(1):建立适当的平面直角坐标系,求出抛物线的函数解析式;y=- x2+2.4(?,1.5)问题(2)离开水面1.5m处,涵洞宽ED是多少?是否会超过1m?离开水面1.5m点题 分析当y=问题(3)小船宽为1m,高为1.5m,能否通过?能否通过?学生讨论y=- x2+2.4问题(3)小船宽为1m,高为1.5m,能否通过?当x=0.5时 得 y=1.46
∵1.46<1.5
∴不能通过
难点:
这里的y值表示的是涵洞的高F(0.5,0)何时获得最大利润 某商店经营T恤衫,将进价为每件8元的商品按每件10元出售时,每天可售出100件。他想采用提高售价的方法来增加利润。经调查发现这种商品每提价1元,每天的销量就会减少10件。
①写出每天所得利润y(元)与售价x(元/件)之间的函数关系式,并写出自变量的取值范围。
②请你帮助分析,销售单价是多少元时,才能使一天的赢利最大?
分析:总利润=单件利润X销量
单件利润=售价- 进价
单件利润=(x-8)元, 销量=100-10(x-10)=(200-10x)件 , 所以总利润y=(x-8)(200-10x元解:①y= =(x-8)(200-10x)= -10x2+280x-1600(10≤x≤20)
答:每件定价14元时,一天所得利润最大。② y=-10x2+280x-1600=-10(x-14)2+360
一个截面为抛物线形的遂道底部宽12米,高6米,如图车辆双向通行,规定车辆必须在中心线右侧距道路边缘2米这一范围内行驶,并保持车辆顶部与遂道有不少于 1/3米的空隙,按如图建立的平面直角坐标系,利用所学函数知识,确定通过隧道车辆的高度限制。分析:确定抛线的顶点坐标及与x轴右交点坐标,设抛物线的顶点式,把右交点坐标代入,可求抛物线解析式;规定车辆必须在中心线物右侧距道路边缘2米这一范围内行驶,即此时车子的右边横坐标为6-2=4,代入解析式求此时的纵坐标,回答题目问题 解:由题意可得,抛物线顶点坐标为C(0,6),与x轴的一个交点 B(6,0), 设抛物线解析式为y=ax2+6, 把B(6,0)代入解析式,得a=-16, 所以抛物线解析式为y=-16x2+6, 由BE=2,OB=6得OE=4,设D(4,y),把x=4代入解析式y=-16x2+6 得y=10/3 ∵10/3-1/3=3米, ∴通过遂道车辆的高度限制为3米。拓展训练某广告公司设计一幅周长12米的矩形广告牌,广告设计费为每平方米1000元。设矩形的一边长为x米,面积为s平方米
(1)求出s与x之间的函数关系式;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用;
(3)为使广告牌美观、大方,要求做成黄金矩形。请你按要求设计,并计算出可获得的设计费是多少? (精确到元)。注:黄金矩形是一个长和宽的比有特殊比例的矩形,很多国家的国旗就是黄金矩形,其长宽之比1.618:1 ,1.618是黄金分割数 答案提示:
①.因为周长是12,一条边是x, 所以另一条边是 6- x,S=x(6-x)( 0③8000元课堂小结找点坐标求解析式解决问题把实际问题转化为点坐标某跳水运动员进行10m跳台跳水训练时,身体(看成一点)在空中的运动路线为下图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件),最高处距水面, ,入水处距池边的距离为4m.在某次跳水时,要求
该运动员在距水面高度为5m或5m以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误. (1)求这条抛物线的解析式;
(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为 3.6m,问此次跳水会不会失误
(3)要是此次试跳不至于失误,该运动员按(1)中抛物线运行,且运动员在空中调整好入水姿势时,距池边的水平距离至多为多少? 思考布置作业
(1)喷出的水流距水平面的最大高度是多少?
(2)如果不计其他因素,那么水池的半径至少为 多少时,才能使喷出的水流都落在水池内?By=-x2+2x+0.8最大高度顶点纵坐标实际问题与函数知识的对应配方得 y= -(x-1)2+1.8由y=-x2+2x+0.8∴最大高度为1.8m喷出的水流距水平面的最大高度是多少?yx水池的半径至少为多少时,才能使喷出的水流都落在水池内?
析题分意:水池为圆形,O点在中央,喷水的落点到圆心的距离相等。最小半径线段OB的长度
(B点的横坐标)∴最小半径为2.34m注意自变量的实际意义BC令y=0,即-(x-1)2+1.8 =0
则x的值为 x1≈2.34 x2≈– 0.34舍去水池的半径至少为多少时,才能使喷出的水流都落在水池内?( 2.236,结果保留两位小数)
(不合题意,舍去)y=-x2+2x+0.8一个涵洞的截面成抛物线形,如图,测得当水面宽AB=1.6m时,涵洞顶点与水面的距离为2.4m,1)建立适当的平面直角坐标系,求出抛物线的函数解析式;2)离开水面1.5m处,涵洞宽ED是多少?是否会超过1m?
3)一只宽为1m,高为1.5m的小船能否通过?为什么?例2点题 分析问题(1):建立适当的平面直角坐标系,求出抛物线的函数解析式;yxO方法1方法2方法3y=- x2+2.4点题 分析问题(1):建立适当的平面直角坐标系,求出抛物线的函数解析式;y=- x2+2.4(?,1.5)问题(2)离开水面1.5m处,涵洞宽ED是多少?是否会超过1m?离开水面1.5m点题 分析当y=问题(3)小船宽为1m,高为1.5m,能否通过?能否通过?学生讨论y=- x2+2.4问题(3)小船宽为1m,高为1.5m,能否通过?当x=0.5时 得 y=1.46
∵1.46<1.5
∴不能通过
难点:
这里的y值表示的是涵洞的高F(0.5,0)何时获得最大利润 某商店经营T恤衫,将进价为每件8元的商品按每件10元出售时,每天可售出100件。他想采用提高售价的方法来增加利润。经调查发现这种商品每提价1元,每天的销量就会减少10件。
①写出每天所得利润y(元)与售价x(元/件)之间的函数关系式,并写出自变量的取值范围。
②请你帮助分析,销售单价是多少元时,才能使一天的赢利最大?
分析:总利润=单件利润X销量
单件利润=售价- 进价
单件利润=(x-8)元, 销量=100-10(x-10)=(200-10x)件 , 所以总利润y=(x-8)(200-10x元解:①y= =(x-8)(200-10x)= -10x2+280x-1600(10≤x≤20)
答:每件定价14元时,一天所得利润最大。② y=-10x2+280x-1600=-10(x-14)2+360
一个截面为抛物线形的遂道底部宽12米,高6米,如图车辆双向通行,规定车辆必须在中心线右侧距道路边缘2米这一范围内行驶,并保持车辆顶部与遂道有不少于 1/3米的空隙,按如图建立的平面直角坐标系,利用所学函数知识,确定通过隧道车辆的高度限制。分析:确定抛线的顶点坐标及与x轴右交点坐标,设抛物线的顶点式,把右交点坐标代入,可求抛物线解析式;规定车辆必须在中心线物右侧距道路边缘2米这一范围内行驶,即此时车子的右边横坐标为6-2=4,代入解析式求此时的纵坐标,回答题目问题 解:由题意可得,抛物线顶点坐标为C(0,6),与x轴的一个交点 B(6,0), 设抛物线解析式为y=ax2+6, 把B(6,0)代入解析式,得a=-16, 所以抛物线解析式为y=-16x2+6, 由BE=2,OB=6得OE=4,设D(4,y),把x=4代入解析式y=-16x2+6 得y=10/3 ∵10/3-1/3=3米, ∴通过遂道车辆的高度限制为3米。拓展训练某广告公司设计一幅周长12米的矩形广告牌,广告设计费为每平方米1000元。设矩形的一边长为x米,面积为s平方米
(1)求出s与x之间的函数关系式;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用;
(3)为使广告牌美观、大方,要求做成黄金矩形。请你按要求设计,并计算出可获得的设计费是多少? (精确到元)。注:黄金矩形是一个长和宽的比有特殊比例的矩形,很多国家的国旗就是黄金矩形,其长宽之比1.618:1 ,1.618是黄金分割数 答案提示:
①.因为周长是12,一条边是x, 所以另一条边是 6- x,S=x(6-x)( 0
该运动员在距水面高度为5m或5m以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误. (1)求这条抛物线的解析式;
(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为 3.6m,问此次跳水会不会失误
(3)要是此次试跳不至于失误,该运动员按(1)中抛物线运行,且运动员在空中调整好入水姿势时,距池边的水平距离至多为多少? 思考布置作业
