19.1函数同步练习(无答案)人教版八年级数学下册
文档属性
| 名称 | 19.1函数同步练习(无答案)人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 570.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 07:57:05 | ||
图片预览

文档简介
人教版八下19.1函数
一、选择题
1、在球的体积公式V=πR3中,下列说法中正确的是 ( )
A、V,π,R是变量,为常量 B、V,π是变量,R为常量
C、V,R是变量,,π为常量 D、以上都不对
2、下列曲线中不能表示y是x的函数的是 ( )
A、 B、 C、 D、
3.小华的爷爷每天坚持体育锻炼.某天他慢步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家,下列能反映当天小华的爷爷离家的距离y与时间x之间函数关系的大致图象是 ( )
4.函数y=中自变量x的取值范围是 ( )
A.x≤2 B.x=3
C.x<2且x≠3 D.x≤2且x≠3
5.如果每盒圆珠笔有12枝,售价18元,那么购买圆珠笔的总金额y(元)与购买圆珠笔的数量x(枝)之间的关系是 ( ).
A.y=x B.y=x C.y=12x D.y=18x
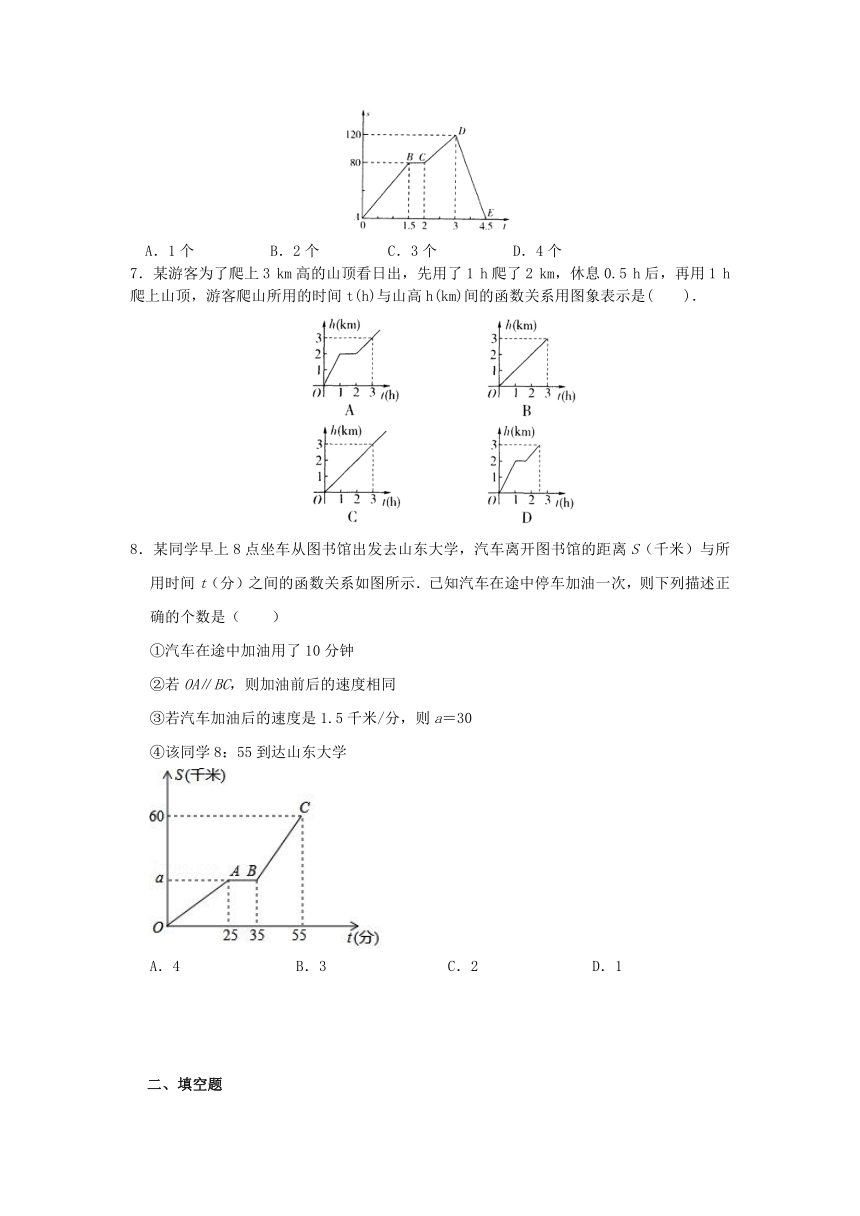
6.图中的折线ABCDE描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(km)和行驶的时间t(h)之间的函数关系,根据图中提供的信息.给出下列说法:①汽车共行驶了120 km;②汽车在行驶途中停留了0.5 h;③汽车在整个行驶过程中的平均速度为km/h;④汽车自出发后3~4.5 h之间行驶的速度在逐渐减少.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
7.某游客为了爬上3 km高的山顶看日出,先用了1 h爬了2 km,休息0.5 h后,再用1 h爬上山顶,游客爬山所用的时间t(h)与山高h(km)间的函数关系用图象表示是( ).
8.某同学早上8点坐车从图书馆出发去山东大学,汽车离开图书馆的距离S(千米)与所用时间t(分)之间的函数关系如图所示.已知汽车在途中停车加油一次,则下列描述正确的个数是( )
①汽车在途中加油用了10分钟
②若OA∥BC,则加油前后的速度相同
③若汽车加油后的速度是1.5千米/分,则a=30
④该同学8:55到达山东大学
A.4 B.3 C.2 D.1
二、填空题
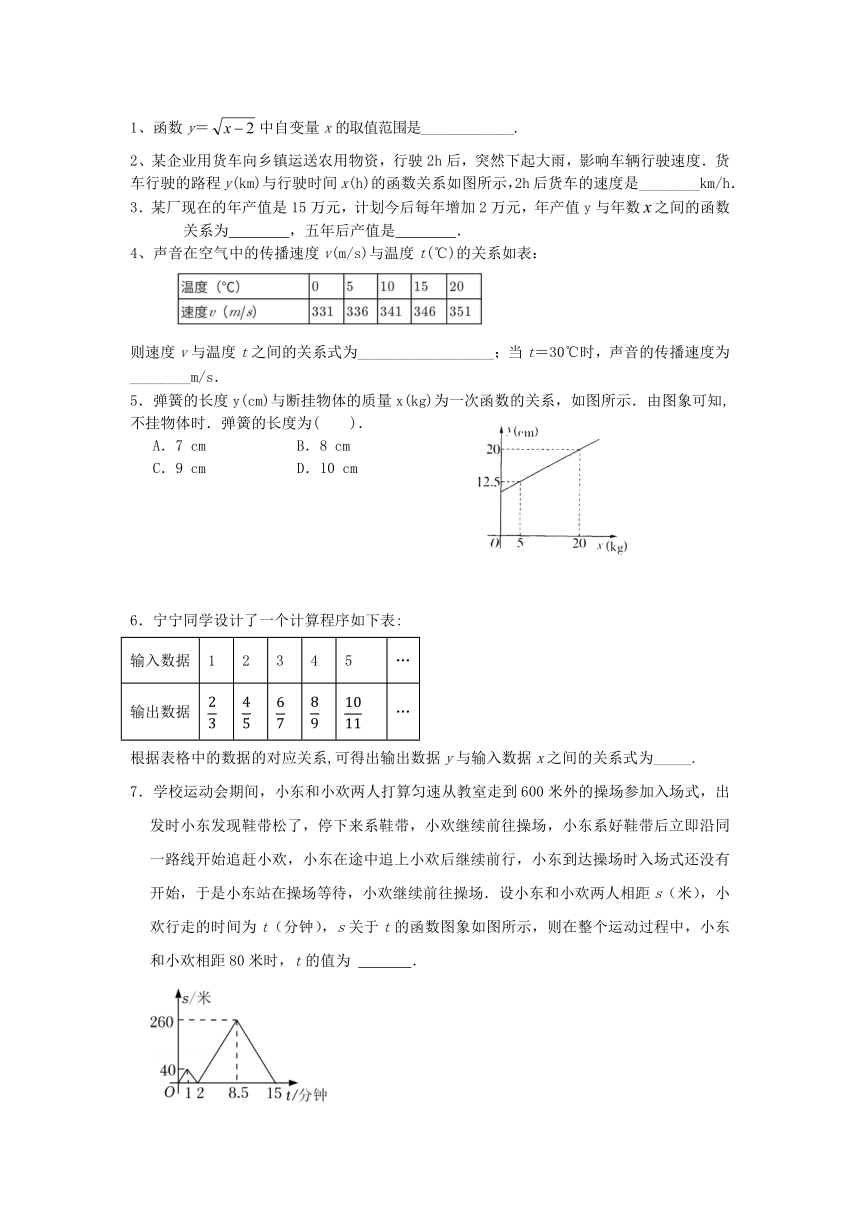
1、函数y=中自变量x的取值范围是_____________.
2、某企业用货车向乡镇运送农用物资,行驶2h后,突然下起大雨,影响车辆行驶速度.货车行驶的路程y(km)与行驶时间x(h)的函数关系如图所示,2h后货车的速度是________km/h.
3.某厂现在的年产值是15万元,计划今后每年增加2万元,年产值y与年数之间的函数关系为 ,五年后产值是 .
4、声音在空气中的传播速度v(m/s)与温度t(℃)的关系如表:
则速度v与温度t之间的关系式为__________________;当t=30℃时,声音的传播速度为________m/s.
5.弹簧的长度y(cm)与断挂物体的质量x(kg)为一次函数的关系,如图所示.由图象可知,不挂物体时.弹簧的长度为( ).
A.7 cm B.8 cm
C.9 cm D.10 cm
6.宁宁同学设计了一个计算程序如下表:
输入数据 1 2 3 4 5 …
输出数据 …
根据表格中的数据的对应关系,可得出输出数据y与输入数据x之间的关系式为_____.
7.学校运动会期间,小东和小欢两人打算匀速从教室走到600米外的操场参加入场式,出发时小东发现鞋带松了,停下来系鞋带,小欢继续前往操场,小东系好鞋带后立即沿同一路线开始追赶小欢,小东在途中追上小欢后继续前行,小东到达操场时入场式还没有开始,于是小东站在操场等待,小欢继续前往操场.设小东和小欢两人相距s(米),小欢行走的时间为t(分钟),s关于t的函数图象如图所示,则在整个运动过程中,小东和小欢相距80米时,t的值为 .
8、如图,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图像如图所示,那么△ABC的面积是________.
9.根据如图所示的程序计算:若输入自变量x的值为,则输出的结果是 .
10.如图1,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,水槽内水面的高度y(cm)与注水时间x(s),又经过 秒恰好将水槽注满.
三、解答题
1.人的大脑所能记忆的内容是有限的,随着时间的推移,记忆的东西会逐渐被遗忘,李老师调查了自己班学生的学习遗忘规律,并根据调查数据描绘了一条曲线(如图所示),其中纵轴表示学习中的记忆保持量,横轴表示时间,观察图象并回答下列问题:
(1)观察图象,1h后,记忆保持量约为 ;8h后,记忆保持量约为 .
(2)图中的A点表示的意义是 ;
(3)在以下哪个时间段内遗忘的速度最快?填序号 ;
①0﹣2h;②2﹣4h;③4﹣6h;④6﹣8h.
(4)有研究表明,如及时复习,一天后能保持98%,根据遗忘曲线,如不复习,结果又怎样?由此,你有什么感受.
2.受疫情的影响,各类学校纷纷延迟开学时间,教育部提倡“停课不停教,线上教育的用户使用量猛增,现“钉钉”平台整理出“线上教学”项目投入资金x及预计利润y如表:
投入资金(亿元) 1 2 3 4 5 6 7
预计利润(千万元) 0.3 0.5 0.7 0.9 1.1 1.3 1.5
(1)如表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果预计获得1.1千万元的利润,投入资金应为 亿元.
(3)如果公司可以拿出10亿元进行“线上教学”项目的投资,预计利润是多少?说说理由.
3.端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程米与时间分钟之间的函数关系图象如图所示,请你根据图象,回答下列问题:
这次龙舟赛的全程是______ 米,______ 队先到达终点;
求乙与甲相遇时乙的速度;
求出在乙队与甲相遇之前,他们何时相距100米?
4.一艘冲锋舟A从甲地匀速航行到乙地,到达乙地后随即勾速返回.该冲锋舟在往返过程中离甲地的距离与行驶时间之间的函数图象如图1所示,请根据图象解答下列问题:
(1)甲、乙两地间的距离是______,往返共用时间是______;
(2)若冲锋舟A从甲地到乙地的速度是,返回时从乙地到甲地的速度是,则与的关系是______(填“”“”或“”);
(3)如图2,若冲锋舟A从甲地去往乙地用时2h,另有一艘冲锋舟B以的速度与冲锋舟A同时从甲地出发前往乙地,求冲锋舟A出发后多长时间与冲锋舟B相遇.
5.某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示:根据图象解答下列问题:
(1)洗衣机的进水时间是 分钟,清洗时洗衣机中的水量是 升.
(2)已知洗衣机的排水速度为每分钟12升,
①求排水时y与x之间的关系式;
②如果排水时间为3分钟,排水结束时洗衣机中剩下的水量为 升.
6.如图1,已知△ABC中,BC=6,P是BC上一动点,沿BC由B向C运动,在这个变化过程中设BP=x,且把x看成自变量
(1)图中哪三角形的面积可以看成是因变量?
(2)设△APC的面积为S,图2刻画的是S随x变化而变化的图象,根据图象回答以下问题:
①图中M点代表的意义是 .
②△ABC的高AF的长为 .
③写出S与x的关系式 .
④a的值为 .
一、选择题
1、在球的体积公式V=πR3中,下列说法中正确的是 ( )
A、V,π,R是变量,为常量 B、V,π是变量,R为常量
C、V,R是变量,,π为常量 D、以上都不对
2、下列曲线中不能表示y是x的函数的是 ( )
A、 B、 C、 D、
3.小华的爷爷每天坚持体育锻炼.某天他慢步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家,下列能反映当天小华的爷爷离家的距离y与时间x之间函数关系的大致图象是 ( )
4.函数y=中自变量x的取值范围是 ( )
A.x≤2 B.x=3
C.x<2且x≠3 D.x≤2且x≠3
5.如果每盒圆珠笔有12枝,售价18元,那么购买圆珠笔的总金额y(元)与购买圆珠笔的数量x(枝)之间的关系是 ( ).
A.y=x B.y=x C.y=12x D.y=18x
6.图中的折线ABCDE描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(km)和行驶的时间t(h)之间的函数关系,根据图中提供的信息.给出下列说法:①汽车共行驶了120 km;②汽车在行驶途中停留了0.5 h;③汽车在整个行驶过程中的平均速度为km/h;④汽车自出发后3~4.5 h之间行驶的速度在逐渐减少.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
7.某游客为了爬上3 km高的山顶看日出,先用了1 h爬了2 km,休息0.5 h后,再用1 h爬上山顶,游客爬山所用的时间t(h)与山高h(km)间的函数关系用图象表示是( ).
8.某同学早上8点坐车从图书馆出发去山东大学,汽车离开图书馆的距离S(千米)与所用时间t(分)之间的函数关系如图所示.已知汽车在途中停车加油一次,则下列描述正确的个数是( )
①汽车在途中加油用了10分钟
②若OA∥BC,则加油前后的速度相同
③若汽车加油后的速度是1.5千米/分,则a=30
④该同学8:55到达山东大学
A.4 B.3 C.2 D.1
二、填空题
1、函数y=中自变量x的取值范围是_____________.
2、某企业用货车向乡镇运送农用物资,行驶2h后,突然下起大雨,影响车辆行驶速度.货车行驶的路程y(km)与行驶时间x(h)的函数关系如图所示,2h后货车的速度是________km/h.
3.某厂现在的年产值是15万元,计划今后每年增加2万元,年产值y与年数之间的函数关系为 ,五年后产值是 .
4、声音在空气中的传播速度v(m/s)与温度t(℃)的关系如表:
则速度v与温度t之间的关系式为__________________;当t=30℃时,声音的传播速度为________m/s.
5.弹簧的长度y(cm)与断挂物体的质量x(kg)为一次函数的关系,如图所示.由图象可知,不挂物体时.弹簧的长度为( ).
A.7 cm B.8 cm
C.9 cm D.10 cm
6.宁宁同学设计了一个计算程序如下表:
输入数据 1 2 3 4 5 …
输出数据 …
根据表格中的数据的对应关系,可得出输出数据y与输入数据x之间的关系式为_____.
7.学校运动会期间,小东和小欢两人打算匀速从教室走到600米外的操场参加入场式,出发时小东发现鞋带松了,停下来系鞋带,小欢继续前往操场,小东系好鞋带后立即沿同一路线开始追赶小欢,小东在途中追上小欢后继续前行,小东到达操场时入场式还没有开始,于是小东站在操场等待,小欢继续前往操场.设小东和小欢两人相距s(米),小欢行走的时间为t(分钟),s关于t的函数图象如图所示,则在整个运动过程中,小东和小欢相距80米时,t的值为 .
8、如图,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图像如图所示,那么△ABC的面积是________.
9.根据如图所示的程序计算:若输入自变量x的值为,则输出的结果是 .
10.如图1,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,水槽内水面的高度y(cm)与注水时间x(s),又经过 秒恰好将水槽注满.
三、解答题
1.人的大脑所能记忆的内容是有限的,随着时间的推移,记忆的东西会逐渐被遗忘,李老师调查了自己班学生的学习遗忘规律,并根据调查数据描绘了一条曲线(如图所示),其中纵轴表示学习中的记忆保持量,横轴表示时间,观察图象并回答下列问题:
(1)观察图象,1h后,记忆保持量约为 ;8h后,记忆保持量约为 .
(2)图中的A点表示的意义是 ;
(3)在以下哪个时间段内遗忘的速度最快?填序号 ;
①0﹣2h;②2﹣4h;③4﹣6h;④6﹣8h.
(4)有研究表明,如及时复习,一天后能保持98%,根据遗忘曲线,如不复习,结果又怎样?由此,你有什么感受.
2.受疫情的影响,各类学校纷纷延迟开学时间,教育部提倡“停课不停教,线上教育的用户使用量猛增,现“钉钉”平台整理出“线上教学”项目投入资金x及预计利润y如表:
投入资金(亿元) 1 2 3 4 5 6 7
预计利润(千万元) 0.3 0.5 0.7 0.9 1.1 1.3 1.5
(1)如表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果预计获得1.1千万元的利润,投入资金应为 亿元.
(3)如果公司可以拿出10亿元进行“线上教学”项目的投资,预计利润是多少?说说理由.
3.端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程米与时间分钟之间的函数关系图象如图所示,请你根据图象,回答下列问题:
这次龙舟赛的全程是______ 米,______ 队先到达终点;
求乙与甲相遇时乙的速度;
求出在乙队与甲相遇之前,他们何时相距100米?
4.一艘冲锋舟A从甲地匀速航行到乙地,到达乙地后随即勾速返回.该冲锋舟在往返过程中离甲地的距离与行驶时间之间的函数图象如图1所示,请根据图象解答下列问题:
(1)甲、乙两地间的距离是______,往返共用时间是______;
(2)若冲锋舟A从甲地到乙地的速度是,返回时从乙地到甲地的速度是,则与的关系是______(填“”“”或“”);
(3)如图2,若冲锋舟A从甲地去往乙地用时2h,另有一艘冲锋舟B以的速度与冲锋舟A同时从甲地出发前往乙地,求冲锋舟A出发后多长时间与冲锋舟B相遇.
5.某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示:根据图象解答下列问题:
(1)洗衣机的进水时间是 分钟,清洗时洗衣机中的水量是 升.
(2)已知洗衣机的排水速度为每分钟12升,
①求排水时y与x之间的关系式;
②如果排水时间为3分钟,排水结束时洗衣机中剩下的水量为 升.
6.如图1,已知△ABC中,BC=6,P是BC上一动点,沿BC由B向C运动,在这个变化过程中设BP=x,且把x看成自变量
(1)图中哪三角形的面积可以看成是因变量?
(2)设△APC的面积为S,图2刻画的是S随x变化而变化的图象,根据图象回答以下问题:
①图中M点代表的意义是 .
②△ABC的高AF的长为 .
③写出S与x的关系式 .
④a的值为 .
