1.1.2空间向量的数量积运算 课件(共20张PPT)——高中数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 1.1.2空间向量的数量积运算 课件(共20张PPT)——高中数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 21:39:31 | ||
图片预览








文档简介
(共20张PPT)
空间向量的数量积运算
一 、基本概念
如图,已知两个非零向量a,6在空间任取一点0,作OA a,
OB 6, 则
1.范围:0 乙
∠AOB叫做向量a 与6的夹角,记作:(a,b>
则称à与b相互垂直,并记作:
3.如果(a,b
π
2
b
b
b
a
a
已知空间两个非零向量a,b, 则 ab cos(a,b)叫 做a,b的数量 积,记作:a.6.
a·B a b cos(a,b>
规定:零向量与任意向量的数量积等于零.
特别的,
基础小测
1.辨析记忆(对的打“ √”,错的打“×”).
(1)向量AB 与CD 的夹角等于向量AB 与DC 的夹角 . ( )
(2)若a ·b=0, 则 a=0 或 b=0. ( )
(3)对于非零向量a,b,(4)若 a·b=b·c, 且b≠0, 则 a=c.()
(5)若a,b 均为非零向量,则a·b=|al|lb|是 a 与b 共 线 的 充 要 条 件 . ( )
1)(λa · 2) b=b.a (交换律) 数量积不满足结合律
3)a (b+C) 二 C .b+a.c (分配律)
数量积运算误区
a·6 a·C→6
若a. k, 则a
a C
若a,b,c 都不为0
数可约吗
可除吗
算可结合吗
C 不可以
不可以 不可以
量积运
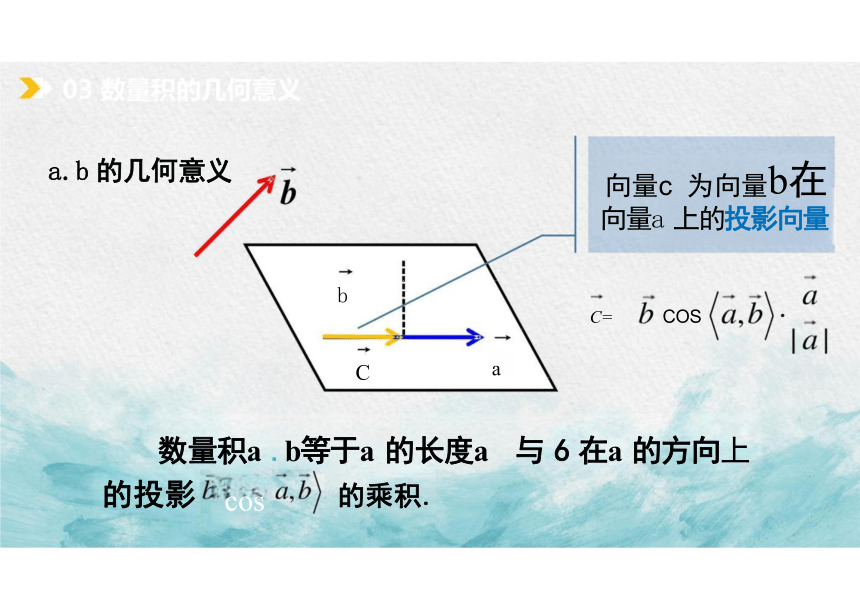
a.b 的几何意义 向量c 为向量b在
向量a 上的投影向量
b
C= COS
C a
数量积a .b等于a 的长度a 与 6 在a 的方向上 的投影 cos 的乘积.
类型 一 空间向量的数量积运算(数学运算)
□题组训练
1.已知向量a 和 b 的夹角为120°,且|a|=2, |b|=5, 则(2a—b) ·a等 于 ( )
2 . 已 知a=3p-2q,b=p +q,p 和 q 是相互垂直的单位向量,则a·b= (
A.1 B . 2 C.3 D . 4
C.4 D.13
B.8+√ 13
A.12
3 . 已知长方体ABCD-A B C D 中 ,AB=AA =2,AD=4,E
为侧面 AB 的中心,F 为
A D 的中点.试计算:(1)BC·ED ;(2)BF·AB ;(3)EF
·FC .
3. 已知空间四边形 ABCD 的每条边和对角线的长都等于 a, 点 E,F 分别是BC,AD
的中点,则AE
A.a B.
·AF 的值为(
a C. a
)
D.
a
教量积的
对手任意的非零向量a,b:
1)a1b a.b=0 证明颜向量垂直的低据
2)a =a-a,a= √a.a求向量的长度(模)的恢据
3)|a.b≤a||b|
的 夹 角 为 ( )
A.30° B.60° C.120° D.150°
P6
5. 已知向量a,b 满足(a+2b)-(a—b)=—6, 且a|=1, |b|=2, 则 a 与b 的夹角
为
工具:
已知两异面直线的方向向量分别为a,b, 且lal=|b|=1, ,则两直线
P4
2.
数量积公式证明垂直 90
工具:a.b=0
证明:
数量积公式证明垂直
类型二 用数量积证明空间垂直关系(逻辑推理)
【典例】如图,在空间四边形0-ABC中 ,OB=0C,AB=AC, 求证:0A⊥BC.
0
A B
)
如图,在正三棱柱ABC-A B C 中,若AB= √2 BB ,则 AB 与BC 所
成角的大小为
角度1 用数量积求角 B
【典例】已知BB ⊥平面ABC,且△ABC是∠B=90° 的等腰直角三角形,四边形
ABB A 和BB C C都是正方形,若AB=a, 求异面直线 BA 与AC所成的角.
∠BAD=90°,∠BAA'=∠DAA'=60°
变式:∠BAD=∠BAA'=∠DAA'=60°
. 求 :AB’,AC '的长
A
在平行六面体ABCD-A'B'℃'D'中,AB=4,AD=3,AA'=5,
2 . 正三棱柱ABC-A B C 的各棱长均为2,E,F 分 别 是AB,A C 的中点,则EF 的 长
C
A E B
( )
B.
C
B
F
A
为
A.2
5 D.
√3
√7
C.
类型三空间向量数量积的应用
角度1利用数量积证明空间中的垂直关系
【典例】已知空间四边形OABC中,∠AOB=∠BOC=∠AOC,且0A=OB=0C,M,N 分别是0A,BC的中点,G是MN的中点,求证:0G⊥BC.
【思维 · 引】利用OA,OB,OC 表示出OG,BC, 证 明OG.BC =0.
【素养 · 探】
利用数量积证明垂直,是空间向量的常见应用,常用到核心素养中的数
学运算.若将典例改为:已知空间四边形ABCD中,AB⊥CD,AC⊥BD,求
证 :AD⊥BC.
角度2利用数量积求距离
【典例】如图所示,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,沿着它的 对角线AC将△ACD折起,使AB与CD成60°角,求此时B,D间的距离.
D
【习练 · 破】
如图,已知一个60°的二面角的棱上有两点A,B,AC,BD 分别是在这两个 面内且垂直于AB的线段.又知AB=4,AC=6,BD=8,求CD的长.
空间向量的数量积运算
一 、基本概念
如图,已知两个非零向量a,6在空间任取一点0,作OA a,
OB 6, 则
1.范围:0 乙
∠AOB叫做向量a 与6的夹角,记作:(a,b>
则称à与b相互垂直,并记作:
3.如果(a,b
π
2
b
b
b
a
a
已知空间两个非零向量a,b, 则 ab cos(a,b)叫 做a,b的数量 积,记作:a.6.
a·B a b cos(a,b>
规定:零向量与任意向量的数量积等于零.
特别的,
基础小测
1.辨析记忆(对的打“ √”,错的打“×”).
(1)向量AB 与CD 的夹角等于向量AB 与DC 的夹角 . ( )
(2)若a ·b=0, 则 a=0 或 b=0. ( )
(3)对于非零向量a,b,
(5)若a,b 均为非零向量,则a·b=|al|lb|是 a 与b 共 线 的 充 要 条 件 . ( )
1)(λa · 2) b=b.a (交换律) 数量积不满足结合律
3)a (b+C) 二 C .b+a.c (分配律)
数量积运算误区
a·6 a·C→6
若a. k, 则a
a C
若a,b,c 都不为0
数可约吗
可除吗
算可结合吗
C 不可以
不可以 不可以
量积运
a.b 的几何意义 向量c 为向量b在
向量a 上的投影向量
b
C= COS
C a
数量积a .b等于a 的长度a 与 6 在a 的方向上 的投影 cos 的乘积.
类型 一 空间向量的数量积运算(数学运算)
□题组训练
1.已知向量a 和 b 的夹角为120°,且|a|=2, |b|=5, 则(2a—b) ·a等 于 ( )
2 . 已 知a=3p-2q,b=p +q,p 和 q 是相互垂直的单位向量,则a·b= (
A.1 B . 2 C.3 D . 4
C.4 D.13
B.8+√ 13
A.12
3 . 已知长方体ABCD-A B C D 中 ,AB=AA =2,AD=4,E
为侧面 AB 的中心,F 为
A D 的中点.试计算:(1)BC·ED ;(2)BF·AB ;(3)EF
·FC .
3. 已知空间四边形 ABCD 的每条边和对角线的长都等于 a, 点 E,F 分别是BC,AD
的中点,则AE
A.a B.
·AF 的值为(
a C. a
)
D.
a
教量积的
对手任意的非零向量a,b:
1)a1b a.b=0 证明颜向量垂直的低据
2)a =a-a,a= √a.a求向量的长度(模)的恢据
3)|a.b≤a||b|
的 夹 角 为 ( )
A.30° B.60° C.120° D.150°
P6
5. 已知向量a,b 满足(a+2b)-(a—b)=—6, 且a|=1, |b|=2, 则 a 与b 的夹角
为
工具:
已知两异面直线的方向向量分别为a,b, 且lal=|b|=1, ,则两直线
P4
2.
数量积公式证明垂直 90
工具:a.b=0
证明:
数量积公式证明垂直
类型二 用数量积证明空间垂直关系(逻辑推理)
【典例】如图,在空间四边形0-ABC中 ,OB=0C,AB=AC, 求证:0A⊥BC.
0
A B
)
如图,在正三棱柱ABC-A B C 中,若AB= √2 BB ,则 AB 与BC 所
成角的大小为
角度1 用数量积求角 B
【典例】已知BB ⊥平面ABC,且△ABC是∠B=90° 的等腰直角三角形,四边形
ABB A 和BB C C都是正方形,若AB=a, 求异面直线 BA 与AC所成的角.
∠BAD=90°,∠BAA'=∠DAA'=60°
变式:∠BAD=∠BAA'=∠DAA'=60°
. 求 :AB’,AC '的长
A
在平行六面体ABCD-A'B'℃'D'中,AB=4,AD=3,AA'=5,
2 . 正三棱柱ABC-A B C 的各棱长均为2,E,F 分 别 是AB,A C 的中点,则EF 的 长
C
A E B
( )
B.
C
B
F
A
为
A.2
5 D.
√3
√7
C.
类型三空间向量数量积的应用
角度1利用数量积证明空间中的垂直关系
【典例】已知空间四边形OABC中,∠AOB=∠BOC=∠AOC,且0A=OB=0C,M,N 分别是0A,BC的中点,G是MN的中点,求证:0G⊥BC.
【思维 · 引】利用OA,OB,OC 表示出OG,BC, 证 明OG.BC =0.
【素养 · 探】
利用数量积证明垂直,是空间向量的常见应用,常用到核心素养中的数
学运算.若将典例改为:已知空间四边形ABCD中,AB⊥CD,AC⊥BD,求
证 :AD⊥BC.
角度2利用数量积求距离
【典例】如图所示,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,沿着它的 对角线AC将△ACD折起,使AB与CD成60°角,求此时B,D间的距离.
D
【习练 · 破】
如图,已知一个60°的二面角的棱上有两点A,B,AC,BD 分别是在这两个 面内且垂直于AB的线段.又知AB=4,AC=6,BD=8,求CD的长.
