1.2空间向量基本定理 课件(共18张PPT)-高中数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 1.2空间向量基本定理 课件(共18张PPT)-高中数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 21:42:21 | ||
图片预览





文档简介
(共18张PPT)
1. 共线向量定理
对空间中任意两个向量a,b(b≠0),a//b
存在实数λ,使a=λb.
用途证明空间三点P,A,B共
的充要条件是
复习回顾
复习回顾
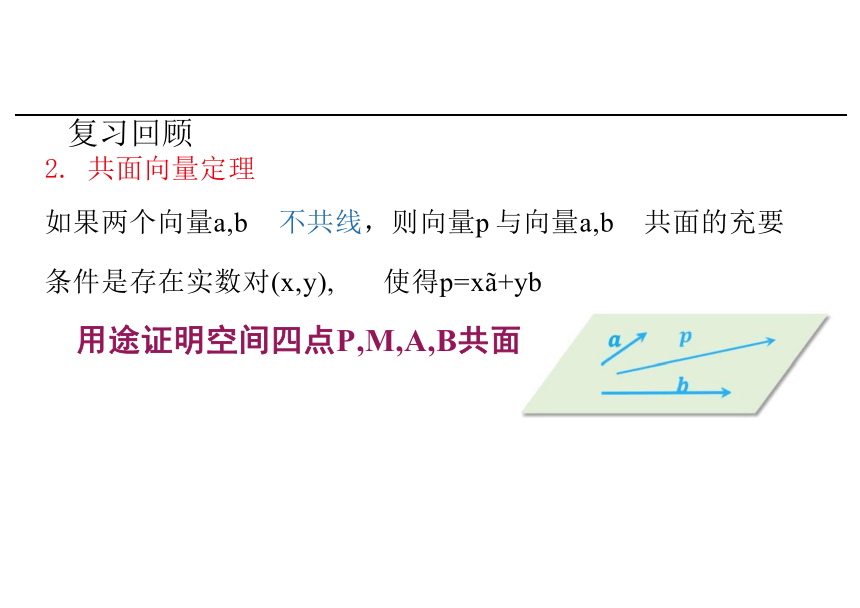
2. 共面向量定理
如果两个向量a,b 不共线,则向量p 与向量a,b 共面的充要
条件是存在实数对(x,y), 使得p=x +yb
用途证明空间四点P,M,A,B共面
复 习 回顾
3.平面向量基本定理:
如果e ,e 是同一平面内的两个不共线向量,那么对于
这一平面内的任一向量a, 有且只有一对实数λ1,λ2, 使a=λ1e +λ e .
e ,e 叫做表示这一平面内所有向量的一组基底.
类似地,任意一个空间向量能否利用任
意三个不共面的向量e ,e ,e 来表示吗
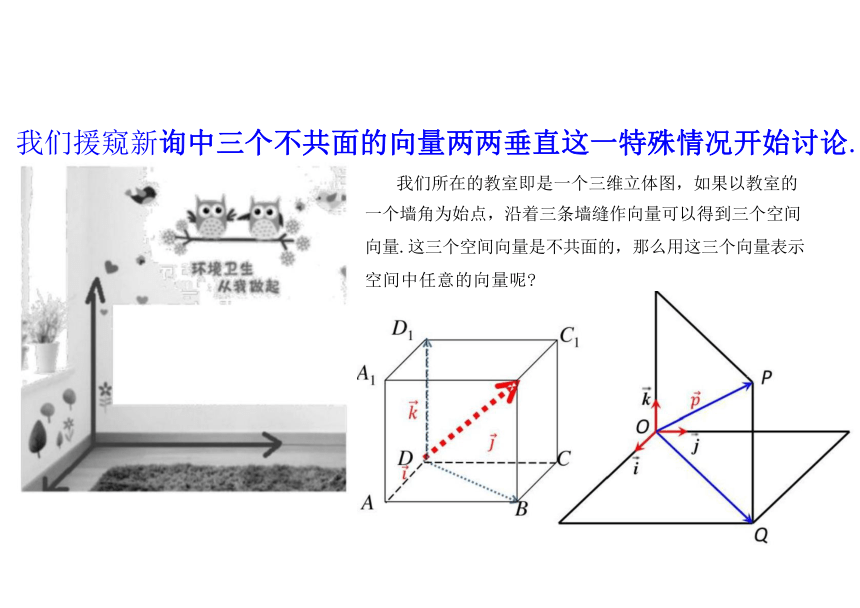
我们所在的教室即是一个三维立体图,如果以教室的
一个墙角为始点,沿着三条墙缝作向量可以得到三个空间 向量.这三个空间向量是不共面的,那么用这三个向量表示 空间中任意的向量呢
我们援窥新询中三个不共面的向量两两垂直这一特殊情况开始讨论.
空间向量的基本定理:
如果三个向量a,b, 二不共面,那么对空间
任一向量 p, 存在一个唯一的有序实数对
{x、y、z},使 p=xa+yb+zc
思路:作 PQ//c,连接0Q
自Q 点作向量a、b的平行线
p=0Q+QP
=xa+yb+zc
基向量:
定理中的a,b,c 确定的一个集合 叫做空
间的一个基底,其中a,b,c 都叫做基向量。
注:1、空间任意三个不共面向量都可以作为空间 向量的一个基底;
2、零向量可视为与任意一个非零向量共线,与任意 两个非零向量共面,所以,三个向量不共面,就隐 含着它们不是零向量;
3、一个基底指一个向量组, 一个基向量指基底中 的某一个向量,二者是相关连的不同概念。
空间向量基本定理
特别地,如果空间的一个基底中的三个基向量两两垂直,且长
度都为1,那么这个基底叫做单位正交基底,常用{i,j,k} 表示.由 空间向量基本定理可知,对空间中的任意向量a, 均可以分解为三 个向量xi,yj,zk, 使 a=xi+yj+zk.
像这样,把一个空间向量分解为三个两两垂直的向量,叫做把
空间向量进行正交分解.
小试牛刀
1. 思考辨析(正确的打“ √ ”,错误的打“×”)
(1)若{0 A,OB,OC}不能构成空间的一个基底,则0,A,B,C 四 点 共 面.( √ )
(2)若{a,b,c}为空间的一个基底,则a,b,c全不是零向量. ( √ )
(3)只有两两垂直的三个向量才能作为空间向量的一组基底. ( × )
2.已知{a,b,c} 是空间的一个基底,则可以和向量p=a+b,q=a—b
构成基底的向量是( D )
A.a B.b C.a+2b D.a+2c
如裸本是面例1OABC的棱BC的中点,点N在线段OM上, 点P在线段AN上,且 ,用OA,OB,OC表示OP
课本12页练习题
1.已知向量{a,b,c} 是空间的一个基底,从a,b,c 中选哪一个向量, 一定可以与向量p=a+b,
q=a—b 构成空间的另一个基底
2.已知O,A,B,C 为空间的四个点,且向量OA,OB,O 不构
成空间的一个基底,那么点0,A,B,C 是否共面
3.如图,已知平行六面体 OABC-O'A'B℃', 点 G 是侧面BB'℃'℃的
中心,且OA=a,OC=b,O0=c.
(1){a,b,c} 是否构成空间的一个基底
(2)如果{a,b,c} 构成空间的一个基底,那么用它表示下列向
(第3题)
量 :OB',BA',CA',OG.
给我一个支点,我可以撬起地球.
— —阿基米德
给我一个基底,
我还你一个空间!
例2 娇图 33,厢六面体ABCD-A,B C D,中,AB=4,AD=4,AA
=5,∠BAA =60°,∠DAA =60°,M,N分别为D C ,C B 的中点.
求证:MN⊥AC .
分析:要证MN⊥AC ,只需证明MN·AC =0.
由已知,{AB,AD,AA }可构成空间的一个基底,
把MN 和AC 分别用基底表示,
然后计算MN·AC 即可.
证明:设AB=a,AD=b,AA =c 这三个向
量不共面,{a,b,c} 构成空间的一个基底,
H
我们用它们表示MN,AC, 则 9
=0
所以MN⊥AC
AC =AB+BC+CC =a+b+c.
如谬本正方例&-A'B'CD的棱长为1,E,F,G 分别为 C'D',A'D',D'D的中点.
(1)求证: EF//AC;(2) 求 CE 与 AG 所成角的余弦值.
解:(1)设 DA=i,DC=j,DD =k, 则{i,j,k}
构成空间的一个单位正交基底.所以
CA=DA-DC=i-j. 所以
.所以EF//AC.
L
C
A B
所以CE 与 AG 所成角的余弦值为
(2)因为
B'
A'
D'
G
C'
5
2
E
2
9
H Aa 工 1 大 H 百
1.已知四面体OABC,OB=OC,∠AOB=∠AOC=θ. 求证:OA⊥BC.
2.如图,在平行六面体ABCD-A'B'C'D′ 中,AB=2,AD=2,AA′=3,∠BAD=∠BAA'=
∠DAA′=60°. 求 BC′ 与CA'所成角的余弦值
3.如图,已知正方体ABCD-A'B℃'D',CD '和DC'相交于点O, 连接AO, 求证AO⊥CD'.
( 第 2 题 )
( 第 3 题 )
1. 共线向量定理
对空间中任意两个向量a,b(b≠0),a//b
存在实数λ,使a=λb.
用途证明空间三点P,A,B共
的充要条件是
复习回顾
复习回顾
2. 共面向量定理
如果两个向量a,b 不共线,则向量p 与向量a,b 共面的充要
条件是存在实数对(x,y), 使得p=x +yb
用途证明空间四点P,M,A,B共面
复 习 回顾
3.平面向量基本定理:
如果e ,e 是同一平面内的两个不共线向量,那么对于
这一平面内的任一向量a, 有且只有一对实数λ1,λ2, 使a=λ1e +λ e .
e ,e 叫做表示这一平面内所有向量的一组基底.
类似地,任意一个空间向量能否利用任
意三个不共面的向量e ,e ,e 来表示吗
我们所在的教室即是一个三维立体图,如果以教室的
一个墙角为始点,沿着三条墙缝作向量可以得到三个空间 向量.这三个空间向量是不共面的,那么用这三个向量表示 空间中任意的向量呢
我们援窥新询中三个不共面的向量两两垂直这一特殊情况开始讨论.
空间向量的基本定理:
如果三个向量a,b, 二不共面,那么对空间
任一向量 p, 存在一个唯一的有序实数对
{x、y、z},使 p=xa+yb+zc
思路:作 PQ//c,连接0Q
自Q 点作向量a、b的平行线
p=0Q+QP
=xa+yb+zc
基向量:
定理中的a,b,c 确定的一个集合 叫做空
间的一个基底,其中a,b,c 都叫做基向量。
注:1、空间任意三个不共面向量都可以作为空间 向量的一个基底;
2、零向量可视为与任意一个非零向量共线,与任意 两个非零向量共面,所以,三个向量不共面,就隐 含着它们不是零向量;
3、一个基底指一个向量组, 一个基向量指基底中 的某一个向量,二者是相关连的不同概念。
空间向量基本定理
特别地,如果空间的一个基底中的三个基向量两两垂直,且长
度都为1,那么这个基底叫做单位正交基底,常用{i,j,k} 表示.由 空间向量基本定理可知,对空间中的任意向量a, 均可以分解为三 个向量xi,yj,zk, 使 a=xi+yj+zk.
像这样,把一个空间向量分解为三个两两垂直的向量,叫做把
空间向量进行正交分解.
小试牛刀
1. 思考辨析(正确的打“ √ ”,错误的打“×”)
(1)若{0 A,OB,OC}不能构成空间的一个基底,则0,A,B,C 四 点 共 面.( √ )
(2)若{a,b,c}为空间的一个基底,则a,b,c全不是零向量. ( √ )
(3)只有两两垂直的三个向量才能作为空间向量的一组基底. ( × )
2.已知{a,b,c} 是空间的一个基底,则可以和向量p=a+b,q=a—b
构成基底的向量是( D )
A.a B.b C.a+2b D.a+2c
如裸本是面例1OABC的棱BC的中点,点N在线段OM上, 点P在线段AN上,且 ,用OA,OB,OC表示OP
课本12页练习题
1.已知向量{a,b,c} 是空间的一个基底,从a,b,c 中选哪一个向量, 一定可以与向量p=a+b,
q=a—b 构成空间的另一个基底
2.已知O,A,B,C 为空间的四个点,且向量OA,OB,O 不构
成空间的一个基底,那么点0,A,B,C 是否共面
3.如图,已知平行六面体 OABC-O'A'B℃', 点 G 是侧面BB'℃'℃的
中心,且OA=a,OC=b,O0=c.
(1){a,b,c} 是否构成空间的一个基底
(2)如果{a,b,c} 构成空间的一个基底,那么用它表示下列向
(第3题)
量 :OB',BA',CA',OG.
给我一个支点,我可以撬起地球.
— —阿基米德
给我一个基底,
我还你一个空间!
例2 娇图 33,厢六面体ABCD-A,B C D,中,AB=4,AD=4,AA
=5,∠BAA =60°,∠DAA =60°,M,N分别为D C ,C B 的中点.
求证:MN⊥AC .
分析:要证MN⊥AC ,只需证明MN·AC =0.
由已知,{AB,AD,AA }可构成空间的一个基底,
把MN 和AC 分别用基底表示,
然后计算MN·AC 即可.
证明:设AB=a,AD=b,AA =c 这三个向
量不共面,{a,b,c} 构成空间的一个基底,
H
我们用它们表示MN,AC, 则 9
=0
所以MN⊥AC
AC =AB+BC+CC =a+b+c.
如谬本正方例&-A'B'CD的棱长为1,E,F,G 分别为 C'D',A'D',D'D的中点.
(1)求证: EF//AC;(2) 求 CE 与 AG 所成角的余弦值.
解:(1)设 DA=i,DC=j,DD =k, 则{i,j,k}
构成空间的一个单位正交基底.所以
CA=DA-DC=i-j. 所以
.所以EF//AC.
L
C
A B
所以CE 与 AG 所成角的余弦值为
(2)因为
B'
A'
D'
G
C'
5
2
E
2
9
H Aa 工 1 大 H 百
1.已知四面体OABC,OB=OC,∠AOB=∠AOC=θ. 求证:OA⊥BC.
2.如图,在平行六面体ABCD-A'B'C'D′ 中,AB=2,AD=2,AA′=3,∠BAD=∠BAA'=
∠DAA′=60°. 求 BC′ 与CA'所成角的余弦值
3.如图,已知正方体ABCD-A'B℃'D',CD '和DC'相交于点O, 连接AO, 求证AO⊥CD'.
( 第 2 题 )
( 第 3 题 )
