1.4.2 用空间向量研究距离、夹角问题 课件(共39张PPT)—— 高中数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 1.4.2 用空间向量研究距离、夹角问题 课件(共39张PPT)—— 高中数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 21:49:17 | ||
图片预览






文档简介
(共39张PPT)
第一章空间向量与立体几何
1. 4.2用空间向量研究距离、 夹角问题
能用向量方法解决点到直线、点到平面、相互
平行的直线、相互平行的直线与平面、相互平
行的平面的距离问题和简单夹角问题,并能描
述解决这一类问题的程序.
学习目标
体会向量方法在研究几何问题中的作用.
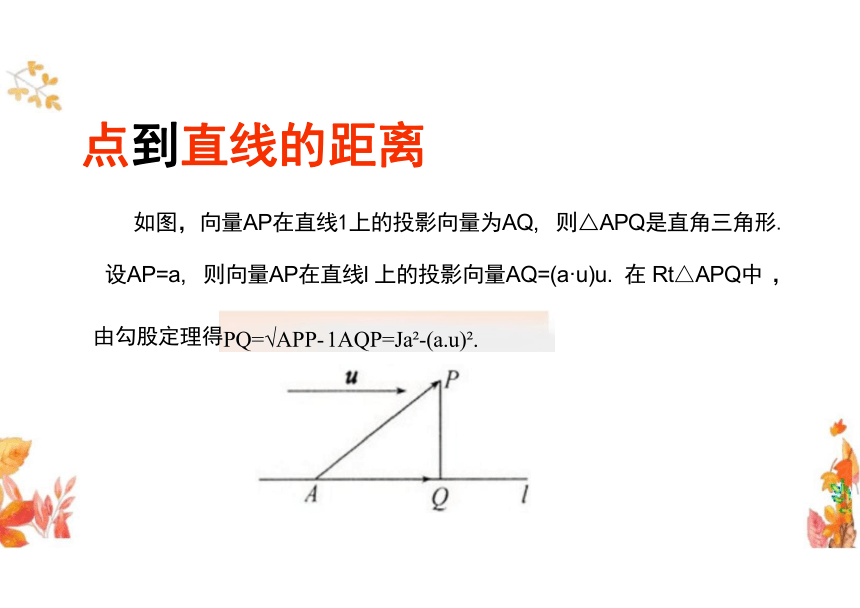
点到直线的距离
如图,向量AP在直线1上的投影向量为AQ, 则△APQ是直角三角形.
设AP=a, 则向量AP在直线l 上的投影向量AQ=(a·u)u. 在 Rt△APQ中 ,
由勾股定理得PQ=√APP- 1AQP=Ja -(a.u) .
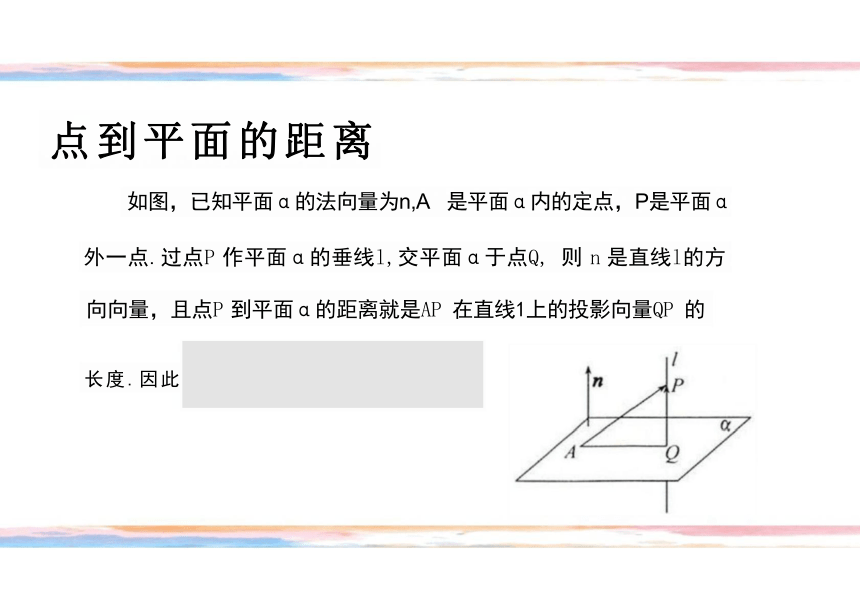
点到平面的距离
如图,已知平面α的法向量为n,A 是平面α内的定点,P是平面α
外一点.过点P 作平面α的垂线l,交平面α于点Q, 则 n 是直线l的方
向向量,且点P 到平面α的距离就是AP 在直线1上的投影向量QP 的
长度.因此
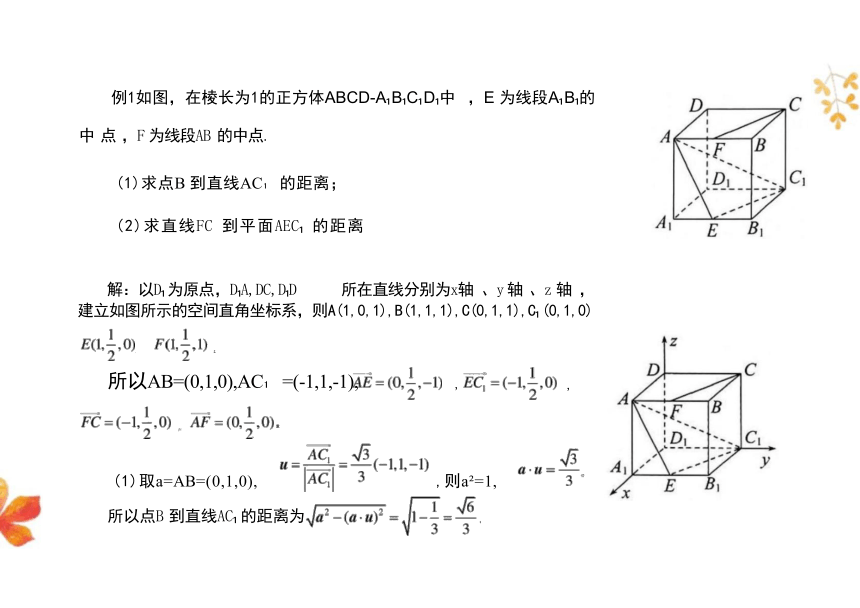
例1如图,在棱长为1的正方体ABCD-A B C D 中 ,E 为线段A B 的
中 点 ,F 为线段AB 的中点.
(1)求点B 到直线AC 的距离;
(2)求直线FC 到平面AEC 的距离
解:以D 为原点,D A,DC,D D 所在直线分别为x轴 、y 轴 、z 轴 , 建立如图所示的空间直角坐标系,则A(1,0,1),B(1,1,1),C(0,1,1),C (0,1,0)
, 1
所以AB=(0,1,0),AC =(-1,1,-1), , ,
重
声
(1)取a=AB=(0,1,0), ,则a =1, 所以点B 到直线AC 的距离为
毒
所 ,所以 , 取z=1, 则 x=1,y=2.
所以n=(1,2,1)是平面AEC 的一个法向量.
又因为
所以点F 到平面AEC 的距离为
即直线FC 到平面AEC 的距离为
所以点F 到平面AEC 的距离即为直线FC 到平面AEC 的距离
,所以FC//EC , 所 以FC// 平面AEC .
设平面 AEC 的法向量为n=(x,y,z), 则
(2)因为
(1)建立立体图形与空间向量的联系,用空间向量表示问
题中涉及的点、直线、平面,把立体几何向题转化为向量问 题 ;
(2)通过向量运算,研究点、直线、平面之间的位置关系
以及它们之间的距离和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
用空间向量解决立体几何问题的“三步曲”
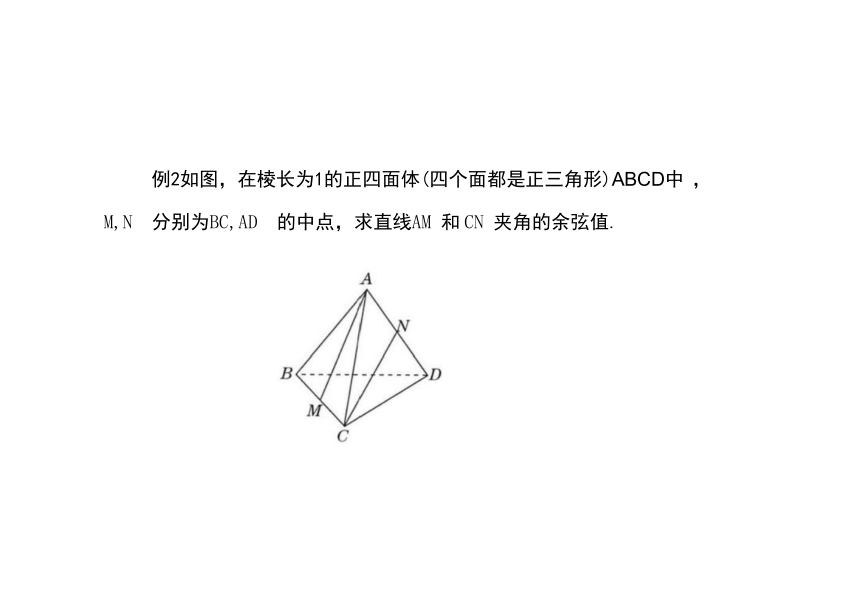
例2如图,在棱长为1的正四面体(四个面都是正三角形)ABCD中 ,
M,N 分别为BC,AD 的中点,求直线AM 和 CN 夹角的余弦值.
又△ABC 和△ACD 均为等边三角形,所以
所以
所以直线AM 和 CN夹角的余弦值为
解:以{CA,CB,CD}作为基底,
则 1
设向量CN与MA 的夹角为θ,则直线AM和 CN夹角的余弦值等于|cosθ|.
事
一般地,两条异面直线所成的角,可以转化为两条异面直线的方向
向量的夹角来求得.也就是说,若异面直线,l 所成的角为θ,其方向
异面直线所成的角
向量分别是u,v, 则
*
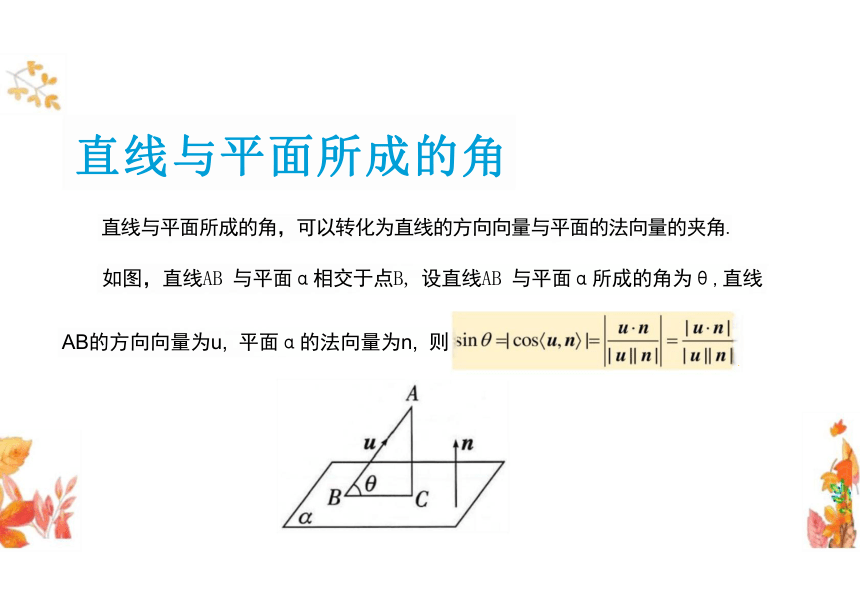
直线与平面所成的角
直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.
如图,直线AB 与平面α相交于点B, 设直线AB 与平面α所成的角为θ,直线
AB的方向向量为u, 平面α的法向量为n, 则
·
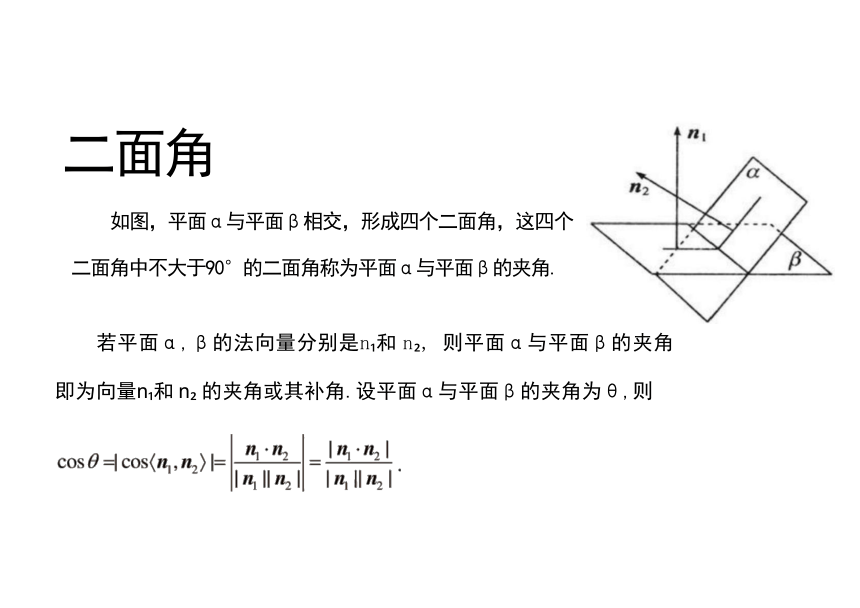
二面角
如图,平面α与平面β相交,形成四个二面角,这四个
二面角中不大于90°的二面角称为平面α与平面β的夹角.
若平面α,β的法向量分别是n 和 n , 则平面α与平面β的夹角
即为向量n 和 n 的夹角或其补角.设平面α与平面β的夹角为θ,则
例3如图,在直三棱柱ABC-A B C 中 ,AC=CB=2 ,AA =3,
∠ACB=90°,P 为BC的中点,点Q,R 分别在棱AA,BB 上 ,AQ=2AQ,
BR=2RB . 求平面PQR 与平面A B C 夹角的余弦值.
解:以C 为 原 点 ,C A ,C B,C C所在直线为x 轴 、y 轴 、z 轴 ,
建立如图所示的空间直角坐标系.
设平面A B C 的法向量为n, 平 面PQR 的法向量为n , 则平面PQR 与
平面A B C 的夹角就是n 与 n 的夹角或其补角
因为C C⊥ 平面A B C, 所以平面A B C 的一个法向量为n =(0,0,1).
根据所建立的空间直角坐标系,可知P(0,1,3),Q(2,0,2),R(0,2,1). 所以PQ=(2,-1,-1),PR=(0,1,-2).
设平面PQR 与平面AB C的夹角为θ,则cosθ=|cos即平面PQR 与平面A B C 的夹角的余弦值为
设n =(x,y,z), 则
取n =(3,4,2), 则
,所以
,所以
例4下图为某种礼物降落伞的示意图,其中有8根绳子和伞面连接,
每根绳子和水平面的法向量的夹角均为30°.已知礼物的质量为1 kg, 每 根
绳子的拉力大小相同.求降落伞在匀速下落的过程中每根绳子拉力的大小
(重力加速度g 取 9.8 m/s ,精确到0.01N).
又因为降落伞匀速下落,所以IF 合I=IG 礼物I=1×9.8=9.8(N)
所以4√3|F|n =9.8.
所以
解:如图,设水平面的单位法向量为n, 其中每一根绳子的拉力均为F.
因为=30°,所 以F 在 n 上的投影向量为
所以8根绳子拉力的合力
垂
( 1 ) 求 证:PA// 平 面EDB;
( 2 ) 求 证:PB⊥ 平 面EFD;
(3)求平面CPB 与平面PBD的夹角的大小.
例5如图,在四棱锥P-ABCD 中,底面 ABCD 是正方形,侧棱PD⊥
底面 ABCD,PD=DC,E 是 PC 的中点,作EF⊥PB 交 PB 于 点F.
解:以D 为原点,DA,DC,DP 所在直线分别为x 轴 、y 轴 、z 轴 ,
建立如图所示的空间直角坐标系.设DC=1.
(1)连接AC, 交 BD 于 点G, 连 接EG.
所以 PA=2EG, 即PA//EG.
而EGc 平面EDB, 且PAa 平面 EDB, 因此PA// 平面 EDB.
故点G 的坐标为 , 且PA=(1,0,-1),
因为底面 ABCD是正方形,所以点G 是它的中心,
依题意得A(1,0,0),P(0,0,1),
事
(2)证明:依题意得B(1,1,0),PB=(1,1,-1).
又 , 故
所以PB⊥DE.
由已知EF⊥PB, 且EF∩DE=E, 所以PB⊥平面EFD.
(3)已知PB⊥EF,由(2)可知 PB⊥DF ,
故∠EFD是平面CPB 与平面PBD 的夹角.
设点F 的坐标为(x,y,z),则 PF=(x,y,z-1).
因为PF=kPB,
所以(x,y,z-1)=k(1,1,-1)=(k,k,-k), 即 x=k,y=k,z=1-k.
设PB·DF=0, 则(1,1,-1)·(k,k,1-k)=k+k-1+k=3k-1=0.
所以 ,点F 的坐标为
又点E 的坐标为 ,所
所以
所以∠EFD=60°,即平面CPB与平面PBD 的夹角大小为60°
(1)综合法:以逻辑推理作为工具解决问题;
(2)向量法:利用向量的概念及其运算解决问题;
(3)坐标法:利用数及其运算来解决问题.
解决立体几何问题的方法
1.若异面直线l,l 的方向向量分别是a=(0,-2,-1) ,b=(2,0,4), 则异面
直线 与 l 所成角的余弦值等于
解析: 设异面直线l 与l 所成的角为θ,a .b=-4,|
.故选B.
课堂小练
a=√5,|b|=2√5,
A_2 A.5
B
D
D.
2.已知棱长为1的正方体ABCD-EFGH, 若 点P 在正方体内部且满足
, 则 点P 到 AB的距离为(
A
口
又AB=(1,0,0),∴AP 在AB 上的投影为
解析:建立如图空间直角坐标系,则
∴ 点P 到 AB 的距离为
.故选A.
则AD 与平面 AA CC 所成的角的正弦值为(
3.在正三棱柱 ABC-A B C 中,已知AB=1,D 在 棱BB 上,且BD=1,
A
则
∵平面ABC⊥平面AA C C,
设AD与平面AAC C所成的角为a,
故选A.
解析:取AC 的中点E, 连
则 ,D(0,0,1),
接BE, 则 BE⊥AC, 如图建立空间直角坐标系Bxyz,
BE⊥AC,∴BE⊥ 平面AA C C,
为平面AA C C 的一个法向量.
则
4.已知菱形ABCD 中,∠ABC=60°, 沿对角线AC 折叠之后,使得平面
BAC⊥ 平 面DAC, 则二面角B-CD-A 的余弦值为(
A.2
日
C.
口
解析:设菱形 ABCD 的边长为1,取 AC 的 中 点O, 连 接BO 、DO, 因 为 ∠ABC=60°,
所以BO⊥AC, 又 平 面BAC⊥ 平面 DAC, 平 面BAC∩平 面DAC=AC, 所 以BO1
令z=1, 得x=√3,y=1, 则 n=(√3,1,1), 易知平面CDA的一个法向量为
设平面BCD 的法向量为n=(x,y,z), 则
平 面ACD, 如图建系,则O(0,0,0),
故 选D.
, 所 以
所以
即
手
申
4
,
5. (多选)已知正方体ABCD-A B C D 的棱长为1,点E、0 分别是
A B 、A C1的中点,P 在正方体内部且满足 则下列说法正确的是
A.点 A 到直线BE 的距离是
B.点 O 到平面ABC D 的距离为
C.平面A BD与平面B CD 间的距离为
D.点 P 到直线AB的距离为
的距离 故A 错误;
易知 ,平面ABC D 的一个法向量DA =(0,-1,1), 则点O
到平面ABC D 的距离 故B 正确;
解析:如图,建立空间直角坐标系,则A(0,0,0),B(1,0,0),D(0,1,0),A (0,0,1),
C (1,1,1),D (0,1,1), ,所以BA=(-1,0,0),
设∠ABE=θ, 则
, 故A到直线BE
AB=(1,0,-1),AD=(0,1,-1),A D =(0,1,0), 设 平 面A BD的法向量为n=(x,y,z),
则 ,所以 令z=1, 得 y=1,x=1, 所 以n=(1,1,1), 所以点D
到平面A BD的距离 因为易证得平面A BD// 平 面B CD,
所以平面A BD 与平面B CD 间的距离等于点D 到平面A BD 的距离,所以平面
A BD与平面B CD 间的距离为
因为
故C 正确;
, 又AB=(1,0,0), 则
所以点P 到 AB 的距离
故 D 错.故选BC.
6.如图,在三棱锥S-ABC 中 ,SA=SB=SC, 且 M,N 分别是AC,SB 的中点,则异面直线SM 与 CN 所成角的余弦值 直线SM 与平面SAB 所成角的大小为
所以以S 为坐标原点,SA,SB,SC 的
方向分别为x 轴 、y 轴 、z 轴的正方向建立空间直角坐标系.设SA=SB=SC=2,
则S(0,0,0),B(0,2,0),A(2,0,0),C(0,0,2),M(1,0,1),N(0,1,0),
所以SM=(1,0,1),CN=(0,1,-2), 所 以
所以异面直线SM 与 CN 所成角的余弦值为
所以直线SM 与平面SAB 所成角的大小为
易得平面SAB 的一个法向量为SC=(0,0,2), 则
所以
7.如图,在四棱锥P-ABCD 中,底面ABCD为直角梯形,BCP AD,
AB⊥BC,∠ADC=45°,PA⊥ 平面ABCD, AB=AP=1,AD=3.
(1)求异面直线PB 与 CD 所成角的大小;
(2)求点D 到平面PBC 的距离.
解析:(1)易得AB,AD,AP 两两互相垂直,故以A 为原点,AB,AD,
AP的方向分别为x 轴 ,y 轴 ,z 轴正方向,建立如图所示的空间直角坐标系,
则P(0,0,1),B(1,0,0),C(1,2,0),D(0,3,0),
所以PB=(1,0,-1),CD=(-1,1,0).
设异面直线PB 与 CD 所成角的大小为θ,
(2)设平面PBC的一个法向量为n=(u,v,w), 由 ( 1 ) 可 得BC=(0,2,0),
则 即 , 取u=w=1, 得 n=(1,0,1),
所以点D 到平面PBC的距离
则
设异面直线PB与CD 所成角的大小为
8.已知四棱柱 ABCD-A B C D 的底面为菱形,AB=AA =2,
AC∩BD=0,AO⊥ 平面A BD,A B=A D.
(1)证明:B Cl/ 平面A BD;
(2)求二面角B-AA -D 的余弦值.
解析:( 1 ) 连 接AB 交A B于点Q, 连接0Q,
易知Q为AB 的中点,O 为AC 的中点,
∴在△AB C中,
∵0Qc 平面A,BD,B C 丈平面A BD,
∴B C//平面A BD.
(2)连接A O,∵AO⊥ 平面A BD,∴AO⊥AO,
∵A B=A D且O为BD 的中点,∴AO⊥BD,
∵AO,BDc 平面ABCD且AONBD=0,∴A O⊥ 平面ABCD.
如图,以O 为坐标原点,OA,OB,OA 所在直线分别为x,y,2 轴,建立空间直角坐标系
结合图形知,二面角B- AA -D 为钝二面角,
∴二面角B-AA -D 的余弦值为
∴AA=(-√3,0,1),AB=(-√3,1,0),
设平面A AB的法向量为n=(x,y,z), 则
令x=1, 得 y=z=√3,∴n=(1,√3,√3).
O-xyz. 易得A(√3,0,0),B(0,1,0),D(0,-1,0),A (0,0,1),
同理可得平面A AD的一个法向量为m=(1,-√3,√3),
,
事
小结:
回顾一下本节课学习了哪些新知识呢
1.点到直线的距离
2.点到平面的距离
3.异面直线所成的角
4.直线与平面所成的角
5.二面角
第一章空间向量与立体几何
1. 4.2用空间向量研究距离、 夹角问题
能用向量方法解决点到直线、点到平面、相互
平行的直线、相互平行的直线与平面、相互平
行的平面的距离问题和简单夹角问题,并能描
述解决这一类问题的程序.
学习目标
体会向量方法在研究几何问题中的作用.
点到直线的距离
如图,向量AP在直线1上的投影向量为AQ, 则△APQ是直角三角形.
设AP=a, 则向量AP在直线l 上的投影向量AQ=(a·u)u. 在 Rt△APQ中 ,
由勾股定理得PQ=√APP- 1AQP=Ja -(a.u) .
点到平面的距离
如图,已知平面α的法向量为n,A 是平面α内的定点,P是平面α
外一点.过点P 作平面α的垂线l,交平面α于点Q, 则 n 是直线l的方
向向量,且点P 到平面α的距离就是AP 在直线1上的投影向量QP 的
长度.因此
例1如图,在棱长为1的正方体ABCD-A B C D 中 ,E 为线段A B 的
中 点 ,F 为线段AB 的中点.
(1)求点B 到直线AC 的距离;
(2)求直线FC 到平面AEC 的距离
解:以D 为原点,D A,DC,D D 所在直线分别为x轴 、y 轴 、z 轴 , 建立如图所示的空间直角坐标系,则A(1,0,1),B(1,1,1),C(0,1,1),C (0,1,0)
, 1
所以AB=(0,1,0),AC =(-1,1,-1), , ,
重
声
(1)取a=AB=(0,1,0), ,则a =1, 所以点B 到直线AC 的距离为
毒
所 ,所以 , 取z=1, 则 x=1,y=2.
所以n=(1,2,1)是平面AEC 的一个法向量.
又因为
所以点F 到平面AEC 的距离为
即直线FC 到平面AEC 的距离为
所以点F 到平面AEC 的距离即为直线FC 到平面AEC 的距离
,所以FC//EC , 所 以FC// 平面AEC .
设平面 AEC 的法向量为n=(x,y,z), 则
(2)因为
(1)建立立体图形与空间向量的联系,用空间向量表示问
题中涉及的点、直线、平面,把立体几何向题转化为向量问 题 ;
(2)通过向量运算,研究点、直线、平面之间的位置关系
以及它们之间的距离和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
用空间向量解决立体几何问题的“三步曲”
例2如图,在棱长为1的正四面体(四个面都是正三角形)ABCD中 ,
M,N 分别为BC,AD 的中点,求直线AM 和 CN 夹角的余弦值.
又△ABC 和△ACD 均为等边三角形,所以
所以
所以直线AM 和 CN夹角的余弦值为
解:以{CA,CB,CD}作为基底,
则 1
设向量CN与MA 的夹角为θ,则直线AM和 CN夹角的余弦值等于|cosθ|.
事
一般地,两条异面直线所成的角,可以转化为两条异面直线的方向
向量的夹角来求得.也就是说,若异面直线,l 所成的角为θ,其方向
异面直线所成的角
向量分别是u,v, 则
*
直线与平面所成的角
直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.
如图,直线AB 与平面α相交于点B, 设直线AB 与平面α所成的角为θ,直线
AB的方向向量为u, 平面α的法向量为n, 则
·
二面角
如图,平面α与平面β相交,形成四个二面角,这四个
二面角中不大于90°的二面角称为平面α与平面β的夹角.
若平面α,β的法向量分别是n 和 n , 则平面α与平面β的夹角
即为向量n 和 n 的夹角或其补角.设平面α与平面β的夹角为θ,则
例3如图,在直三棱柱ABC-A B C 中 ,AC=CB=2 ,AA =3,
∠ACB=90°,P 为BC的中点,点Q,R 分别在棱AA,BB 上 ,AQ=2AQ,
BR=2RB . 求平面PQR 与平面A B C 夹角的余弦值.
解:以C 为 原 点 ,C A ,C B,C C所在直线为x 轴 、y 轴 、z 轴 ,
建立如图所示的空间直角坐标系.
设平面A B C 的法向量为n, 平 面PQR 的法向量为n , 则平面PQR 与
平面A B C 的夹角就是n 与 n 的夹角或其补角
因为C C⊥ 平面A B C, 所以平面A B C 的一个法向量为n =(0,0,1).
根据所建立的空间直角坐标系,可知P(0,1,3),Q(2,0,2),R(0,2,1). 所以PQ=(2,-1,-1),PR=(0,1,-2).
设平面PQR 与平面AB C的夹角为θ,则cosθ=|cos
设n =(x,y,z), 则
取n =(3,4,2), 则
,所以
,所以
例4下图为某种礼物降落伞的示意图,其中有8根绳子和伞面连接,
每根绳子和水平面的法向量的夹角均为30°.已知礼物的质量为1 kg, 每 根
绳子的拉力大小相同.求降落伞在匀速下落的过程中每根绳子拉力的大小
(重力加速度g 取 9.8 m/s ,精确到0.01N).
又因为降落伞匀速下落,所以IF 合I=IG 礼物I=1×9.8=9.8(N)
所以4√3|F|n =9.8.
所以
解:如图,设水平面的单位法向量为n, 其中每一根绳子的拉力均为F.
因为
所以8根绳子拉力的合力
垂
( 1 ) 求 证:PA// 平 面EDB;
( 2 ) 求 证:PB⊥ 平 面EFD;
(3)求平面CPB 与平面PBD的夹角的大小.
例5如图,在四棱锥P-ABCD 中,底面 ABCD 是正方形,侧棱PD⊥
底面 ABCD,PD=DC,E 是 PC 的中点,作EF⊥PB 交 PB 于 点F.
解:以D 为原点,DA,DC,DP 所在直线分别为x 轴 、y 轴 、z 轴 ,
建立如图所示的空间直角坐标系.设DC=1.
(1)连接AC, 交 BD 于 点G, 连 接EG.
所以 PA=2EG, 即PA//EG.
而EGc 平面EDB, 且PAa 平面 EDB, 因此PA// 平面 EDB.
故点G 的坐标为 , 且PA=(1,0,-1),
因为底面 ABCD是正方形,所以点G 是它的中心,
依题意得A(1,0,0),P(0,0,1),
事
(2)证明:依题意得B(1,1,0),PB=(1,1,-1).
又 , 故
所以PB⊥DE.
由已知EF⊥PB, 且EF∩DE=E, 所以PB⊥平面EFD.
(3)已知PB⊥EF,由(2)可知 PB⊥DF ,
故∠EFD是平面CPB 与平面PBD 的夹角.
设点F 的坐标为(x,y,z),则 PF=(x,y,z-1).
因为PF=kPB,
所以(x,y,z-1)=k(1,1,-1)=(k,k,-k), 即 x=k,y=k,z=1-k.
设PB·DF=0, 则(1,1,-1)·(k,k,1-k)=k+k-1+k=3k-1=0.
所以 ,点F 的坐标为
又点E 的坐标为 ,所
所以
所以∠EFD=60°,即平面CPB与平面PBD 的夹角大小为60°
(1)综合法:以逻辑推理作为工具解决问题;
(2)向量法:利用向量的概念及其运算解决问题;
(3)坐标法:利用数及其运算来解决问题.
解决立体几何问题的方法
1.若异面直线l,l 的方向向量分别是a=(0,-2,-1) ,b=(2,0,4), 则异面
直线 与 l 所成角的余弦值等于
解析: 设异面直线l 与l 所成的角为θ,a .b=-4,|
.故选B.
课堂小练
a=√5,|b|=2√5,
A_2 A.5
B
D
D.
2.已知棱长为1的正方体ABCD-EFGH, 若 点P 在正方体内部且满足
, 则 点P 到 AB的距离为(
A
口
又AB=(1,0,0),∴AP 在AB 上的投影为
解析:建立如图空间直角坐标系,则
∴ 点P 到 AB 的距离为
.故选A.
则AD 与平面 AA CC 所成的角的正弦值为(
3.在正三棱柱 ABC-A B C 中,已知AB=1,D 在 棱BB 上,且BD=1,
A
则
∵平面ABC⊥平面AA C C,
设AD与平面AAC C所成的角为a,
故选A.
解析:取AC 的中点E, 连
则 ,D(0,0,1),
接BE, 则 BE⊥AC, 如图建立空间直角坐标系Bxyz,
BE⊥AC,∴BE⊥ 平面AA C C,
为平面AA C C 的一个法向量.
则
4.已知菱形ABCD 中,∠ABC=60°, 沿对角线AC 折叠之后,使得平面
BAC⊥ 平 面DAC, 则二面角B-CD-A 的余弦值为(
A.2
日
C.
口
解析:设菱形 ABCD 的边长为1,取 AC 的 中 点O, 连 接BO 、DO, 因 为 ∠ABC=60°,
所以BO⊥AC, 又 平 面BAC⊥ 平面 DAC, 平 面BAC∩平 面DAC=AC, 所 以BO1
令z=1, 得x=√3,y=1, 则 n=(√3,1,1), 易知平面CDA的一个法向量为
设平面BCD 的法向量为n=(x,y,z), 则
平 面ACD, 如图建系,则O(0,0,0),
故 选D.
, 所 以
所以
即
手
申
4
,
5. (多选)已知正方体ABCD-A B C D 的棱长为1,点E、0 分别是
A B 、A C1的中点,P 在正方体内部且满足 则下列说法正确的是
A.点 A 到直线BE 的距离是
B.点 O 到平面ABC D 的距离为
C.平面A BD与平面B CD 间的距离为
D.点 P 到直线AB的距离为
的距离 故A 错误;
易知 ,平面ABC D 的一个法向量DA =(0,-1,1), 则点O
到平面ABC D 的距离 故B 正确;
解析:如图,建立空间直角坐标系,则A(0,0,0),B(1,0,0),D(0,1,0),A (0,0,1),
C (1,1,1),D (0,1,1), ,所以BA=(-1,0,0),
设∠ABE=θ, 则
, 故A到直线BE
AB=(1,0,-1),AD=(0,1,-1),A D =(0,1,0), 设 平 面A BD的法向量为n=(x,y,z),
则 ,所以 令z=1, 得 y=1,x=1, 所 以n=(1,1,1), 所以点D
到平面A BD的距离 因为易证得平面A BD// 平 面B CD,
所以平面A BD 与平面B CD 间的距离等于点D 到平面A BD 的距离,所以平面
A BD与平面B CD 间的距离为
因为
故C 正确;
, 又AB=(1,0,0), 则
所以点P 到 AB 的距离
故 D 错.故选BC.
6.如图,在三棱锥S-ABC 中 ,SA=SB=SC, 且 M,N 分别是AC,SB 的中点,则异面直线SM 与 CN 所成角的余弦值 直线SM 与平面SAB 所成角的大小为
所以以S 为坐标原点,SA,SB,SC 的
方向分别为x 轴 、y 轴 、z 轴的正方向建立空间直角坐标系.设SA=SB=SC=2,
则S(0,0,0),B(0,2,0),A(2,0,0),C(0,0,2),M(1,0,1),N(0,1,0),
所以SM=(1,0,1),CN=(0,1,-2), 所 以
所以异面直线SM 与 CN 所成角的余弦值为
所以直线SM 与平面SAB 所成角的大小为
易得平面SAB 的一个法向量为SC=(0,0,2), 则
所以
7.如图,在四棱锥P-ABCD 中,底面ABCD为直角梯形,BCP AD,
AB⊥BC,∠ADC=45°,PA⊥ 平面ABCD, AB=AP=1,AD=3.
(1)求异面直线PB 与 CD 所成角的大小;
(2)求点D 到平面PBC 的距离.
解析:(1)易得AB,AD,AP 两两互相垂直,故以A 为原点,AB,AD,
AP的方向分别为x 轴 ,y 轴 ,z 轴正方向,建立如图所示的空间直角坐标系,
则P(0,0,1),B(1,0,0),C(1,2,0),D(0,3,0),
所以PB=(1,0,-1),CD=(-1,1,0).
设异面直线PB 与 CD 所成角的大小为θ,
(2)设平面PBC的一个法向量为n=(u,v,w), 由 ( 1 ) 可 得BC=(0,2,0),
则 即 , 取u=w=1, 得 n=(1,0,1),
所以点D 到平面PBC的距离
则
设异面直线PB与CD 所成角的大小为
8.已知四棱柱 ABCD-A B C D 的底面为菱形,AB=AA =2,
AC∩BD=0,AO⊥ 平面A BD,A B=A D.
(1)证明:B Cl/ 平面A BD;
(2)求二面角B-AA -D 的余弦值.
解析:( 1 ) 连 接AB 交A B于点Q, 连接0Q,
易知Q为AB 的中点,O 为AC 的中点,
∴在△AB C中,
∵0Qc 平面A,BD,B C 丈平面A BD,
∴B C//平面A BD.
(2)连接A O,∵AO⊥ 平面A BD,∴AO⊥AO,
∵A B=A D且O为BD 的中点,∴AO⊥BD,
∵AO,BDc 平面ABCD且AONBD=0,∴A O⊥ 平面ABCD.
如图,以O 为坐标原点,OA,OB,OA 所在直线分别为x,y,2 轴,建立空间直角坐标系
结合图形知,二面角B- AA -D 为钝二面角,
∴二面角B-AA -D 的余弦值为
∴AA=(-√3,0,1),AB=(-√3,1,0),
设平面A AB的法向量为n=(x,y,z), 则
令x=1, 得 y=z=√3,∴n=(1,√3,√3).
O-xyz. 易得A(√3,0,0),B(0,1,0),D(0,-1,0),A (0,0,1),
同理可得平面A AD的一个法向量为m=(1,-√3,√3),
,
事
小结:
回顾一下本节课学习了哪些新知识呢
1.点到直线的距离
2.点到平面的距离
3.异面直线所成的角
4.直线与平面所成的角
5.二面角
