2.2.1 直线的点斜式方程 课件(共16张PPT)—— 高中数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.2.1 直线的点斜式方程 课件(共16张PPT)—— 高中数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 21:54:18 | ||
图片预览






文档简介
(共16张PPT)
第二章直线和圆的方程
2.2.1直线的点斜式方程
01 掌握直线方程的点斜式与斜截式方程.
02 了解斜截式方程与一次函数的关系.
学习目标
由直线上一个定点(x ,y ) 及该直线的斜率k 确定
叫做直线的点斜式方程,简称点斜式.
直线的点斜式方程
方程y-yo=k(x-x )
方程y-y =k(x-x )
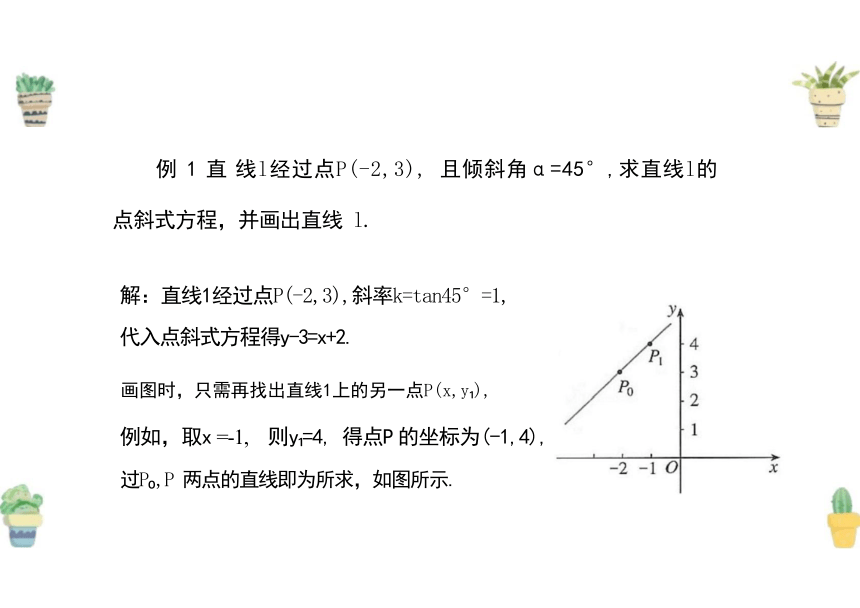
解:直线1经过点P(-2,3),斜率k=tan45°=1,
代入点斜式方程得y-3=x+2.
画图时,只需再找出直线1上的另一点P(x,y ),
例如,取x =-1, 则y =4, 得点P 的坐标为(-1,4),
过P ,P 两点的直线即为所求,如图所示.
例 1 直 线l经过点P(-2,3), 且倾斜角α=45°,求直线l的
点斜式方程,并画出直线 l.
直线l与 y 轴的交点(0,b)的纵坐标b 叫做直线l在 y 轴上的截距.
这样,方程y=kx+b 由直线的斜率k 与它在y 轴上的截距b 确定,
方程y=kx+b 叫做直线的斜截式方程,简称斜截式. 其 中 ,k 是直线的斜率,b 是直线在y 轴上的截距.
直线的斜截式方程
解:(1) 若l//l , 则k=k ,此时l,l 与y 轴的交点不同,即b ≠b ;
反之,若k =k , 且b ≠b , 则 // l .
(2)若l⊥l ,则k k =-1; 反之,若k k =-1, 则l⊥l .
例2已知直线l:y=k x+b ,l :y=k x+
(1)l 1/l 的条件是什么
(2)l⊥l 的条件是什么
b ,试讨论:
由例2可得,对于直线l:y=k x+b , l :y=k x+b ,
l //l → k =k , 且b ≠b ;
l⊥l →k k =-1.
解析:由已知可得直线的点斜式方程为
故选C.
1.过点(3,2),斜率是 的直线方程是(
课堂练习
C.2x-3y=0 D.3x-2y=0
整理得2x-3y=0.
2.已知直线的倾斜角为60°,在y 轴上的截距为-2,则此直线的方程为(
A.y=√3x+2 B.y=-√3x+2
C.y=-√3x-2 D.y=√3x-2
解析:直线的倾斜角为60°,则其斜率为 √3,利用斜截式得直线的方程为y= √3x-2.
故选D.
3.直线x=√3y-1的斜率和在y轴上的截距分别为(
B.√3,-1 C.
解析:将x= √3y-1化为斜截式为
在 y 轴上的截距为 , 故 选C.
即该直线的斜率为
D.√3,
A
则其斜率k 的取值范围是(
A.(-0,-3)U(1,+00)
4.若直线l 经过点P(2,3), 且 在x 轴上的截距的取值范围是(-1,3),
∵直线l 与线段MN 相交(不包含端点),∴k>1 或 k<-3. 故选A.
解析:取x 轴上的点M(-1,0),N(3,0), 则
C.(-3,1)
事
事
解析:直线l的方程可化为y=(a-1)x+3a-2, 由直线l 在y轴上的截距为6,
可得3a-2=6, 解得
5.直线l 的方程为y-a=(a- 1)(x+2), 若直线l 在y 轴上的截距为6,则
6.已知直线l过 点P(2,1), 且 直 线l 的倾斜角为直线 的倾斜角的 2倍,则直线l 的点斜式方程为
,k=tanβ=tan2α=12tan a=5
又直线l 过点P(2,1), 所以直线l 的点斜式方程为
,得斜率为 ,设直线
倾斜角为β,斜率为k, 则
的倾斜角为α,直线l 的
解析:由
7.已知直线l的斜率为 且和两坐标轴围成面积为3的三角形, 则直线l的斜截式方程为
解析:设直线l的方程为
当y=0 时 ,x=-6b, 由题意可得
故直线1的方程为 或
当x=0 时 ,y=b;
,即6 |bl =6, 解得b=±1,
8.求满足下列条件的实数m 的值.
(1)直线l:y=-x+1 与直线l :y=(m -2)x+2m
(2)直线l:y=-2x+3 与直线l :y=(2m-1)x-5
解析:(1)∵Y//l ,∴两直线斜率相等且在y 轴上的截距不相等.
∴m -2=-1 且2m≠1,∴m=±1.
平行;
垂直.
(2)∵I ⊥l ,∴(2m-1)×(-2)=-1,
.
小结:
回顾一下本节课学习了哪些新知识呢
1.直线的点斜式方程
2.直线的斜截式方程
第二章直线和圆的方程
2.2.1直线的点斜式方程
01 掌握直线方程的点斜式与斜截式方程.
02 了解斜截式方程与一次函数的关系.
学习目标
由直线上一个定点(x ,y ) 及该直线的斜率k 确定
叫做直线的点斜式方程,简称点斜式.
直线的点斜式方程
方程y-yo=k(x-x )
方程y-y =k(x-x )
解:直线1经过点P(-2,3),斜率k=tan45°=1,
代入点斜式方程得y-3=x+2.
画图时,只需再找出直线1上的另一点P(x,y ),
例如,取x =-1, 则y =4, 得点P 的坐标为(-1,4),
过P ,P 两点的直线即为所求,如图所示.
例 1 直 线l经过点P(-2,3), 且倾斜角α=45°,求直线l的
点斜式方程,并画出直线 l.
直线l与 y 轴的交点(0,b)的纵坐标b 叫做直线l在 y 轴上的截距.
这样,方程y=kx+b 由直线的斜率k 与它在y 轴上的截距b 确定,
方程y=kx+b 叫做直线的斜截式方程,简称斜截式. 其 中 ,k 是直线的斜率,b 是直线在y 轴上的截距.
直线的斜截式方程
解:(1) 若l//l , 则k=k ,此时l,l 与y 轴的交点不同,即b ≠b ;
反之,若k =k , 且b ≠b , 则 // l .
(2)若l⊥l ,则k k =-1; 反之,若k k =-1, 则l⊥l .
例2已知直线l:y=k x+b ,l :y=k x+
(1)l 1/l 的条件是什么
(2)l⊥l 的条件是什么
b ,试讨论:
由例2可得,对于直线l:y=k x+b , l :y=k x+b ,
l //l → k =k , 且b ≠b ;
l⊥l →k k =-1.
解析:由已知可得直线的点斜式方程为
故选C.
1.过点(3,2),斜率是 的直线方程是(
课堂练习
C.2x-3y=0 D.3x-2y=0
整理得2x-3y=0.
2.已知直线的倾斜角为60°,在y 轴上的截距为-2,则此直线的方程为(
A.y=√3x+2 B.y=-√3x+2
C.y=-√3x-2 D.y=√3x-2
解析:直线的倾斜角为60°,则其斜率为 √3,利用斜截式得直线的方程为y= √3x-2.
故选D.
3.直线x=√3y-1的斜率和在y轴上的截距分别为(
B.√3,-1 C.
解析:将x= √3y-1化为斜截式为
在 y 轴上的截距为 , 故 选C.
即该直线的斜率为
D.√3,
A
则其斜率k 的取值范围是(
A.(-0,-3)U(1,+00)
4.若直线l 经过点P(2,3), 且 在x 轴上的截距的取值范围是(-1,3),
∵直线l 与线段MN 相交(不包含端点),∴k>1 或 k<-3. 故选A.
解析:取x 轴上的点M(-1,0),N(3,0), 则
C.(-3,1)
事
事
解析:直线l的方程可化为y=(a-1)x+3a-2, 由直线l 在y轴上的截距为6,
可得3a-2=6, 解得
5.直线l 的方程为y-a=(a- 1)(x+2), 若直线l 在y 轴上的截距为6,则
6.已知直线l过 点P(2,1), 且 直 线l 的倾斜角为直线 的倾斜角的 2倍,则直线l 的点斜式方程为
,k=tanβ=tan2α=12tan a=5
又直线l 过点P(2,1), 所以直线l 的点斜式方程为
,得斜率为 ,设直线
倾斜角为β,斜率为k, 则
的倾斜角为α,直线l 的
解析:由
7.已知直线l的斜率为 且和两坐标轴围成面积为3的三角形, 则直线l的斜截式方程为
解析:设直线l的方程为
当y=0 时 ,x=-6b, 由题意可得
故直线1的方程为 或
当x=0 时 ,y=b;
,即6 |bl =6, 解得b=±1,
8.求满足下列条件的实数m 的值.
(1)直线l:y=-x+1 与直线l :y=(m -2)x+2m
(2)直线l:y=-2x+3 与直线l :y=(2m-1)x-5
解析:(1)∵Y//l ,∴两直线斜率相等且在y 轴上的截距不相等.
∴m -2=-1 且2m≠1,∴m=±1.
平行;
垂直.
(2)∵I ⊥l ,∴(2m-1)×(-2)=-1,
.
小结:
回顾一下本节课学习了哪些新知识呢
1.直线的点斜式方程
2.直线的斜截式方程
