2.2.3直线的一般式方程 课件(共28张PPT)——高中数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.2.3直线的一般式方程 课件(共28张PPT)——高中数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 22:02:06 | ||
图片预览








文档简介
(共28张PPT)
名 称 几 何 条 件 方程
局限性
点斜式 点P (x ,y )和斜率k y-y =k(x-x,)
不垂直于x
轴
斜截式 斜率k,y轴上的纵截距b 12— r⊥ y-N1U
不垂直于x
轴
两点式 点P(x,y)和点P (x,y
不垂直于x轴
和y轴
截距式 在x轴上的截距a 在y轴上的截距b
不垂直于x、y轴的直
不过原点的直线
复习回顾
直线方程的四种形式:
载
直线与二元一次方程是否都有这种关系呢
下面我们探讨这个问题.
观察直线的点斜式、斜截式、两点式、截距式方程,我 们发现,它们都是关于x,y 的二元一次方程。比如:
y-y =k(x-x )—
y=kx+b —
y-y =x-x
y -y X -X (y -Y )x+(x -x )y+x(y -y )+y(x -x )=0
→kx+(-1)y+y -kx
kx+(-1)y+b=0
=0
1.掌握直 线的一般 式方程. 2.理解关于x,y的二 元一次方程Ax+By 十C=0(A,B不同时
3.会进行直线方
程的五种形式之 间的转化。
为0)都表示直线.
首称
(1).平面直角坐标系中的每一条直线都可以用 一个关于x,y的二元一次方程表示吗
(2).每一个关于x,y的二元一次方程都表示一
条直线吗
先看问题(1),任意一条直线l,在其上任取一点P(x ,y ), 当直线的斜率为k时(此时直线的倾斜角α≠90°),
其方程为 y-y =k(x-x ),
这是关于x,y 的二元一次方程.
当直线的斜率不存在,即直线l的倾斜角α=90°,直线的方程为
x-x =0
上述方程可以认为是关于x,y 的二元一次方程,因为此时方程中y的系数
为0. 方程y-y。=k(x-x ) 和x-x =0 都是二元一次方程,
因此平面直角坐标系中的任意一条直线都可以用一个
关于x,y 的二元一次方程表示.
反之,对于任意一个二元一次方程Ax+By+C=0(A,B 不同时为0),
如果能把它化为直线方程的某种形式,那么我们就可以断定它表示 一条直线.
当B≠0 时,方程Ax+By+C=0 可变形为 9
它表示过点 ,斜率为 的直线.
当B=0 时,A≠0, 方程Ax+By+C=0 可变形为
它表示过点 且垂直于x轴的直线
·由上可知,关于x,y的二元一次方程都表示一条直线.
直线的一般式方程:
我们把关于x,y的二元一次方程
Ax+By+C=0
(其中A,B不同时为0)叫做直线的一般式方程,简称一般式(general form)
注意:对于直线方程的一般式, 一般作如下约定:
1)x的系数为正;
2)x,y的系数及常数项一般不出现分数;
3)按含x项,含y项、常数项顺序排列. 4)没有特别说明,都要写成一般式
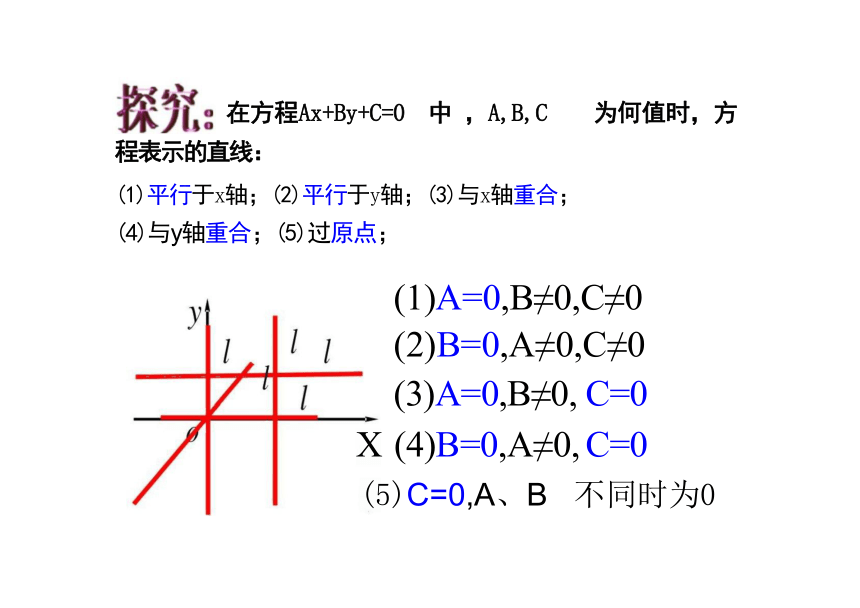
在方程Ax+By+C=0 中 ,A,B,C 为何值时,方
程表示的直线:
(1)平行于x轴;(2)平行于y轴;(3)与x轴重合;
(4)与y轴重合;(5)过原点;
(1)A=0,B≠0,C≠0
(2)B=0,A≠0,C≠0 (3)A=0,B≠0, C=0
X (4)B=0,A≠0, C=0
(5)C=0,A、B 不同时为0
例5已知直线经过点A(6,-4),斜率为 ,求直线的点斜式和一般式方程.
解:经过点A(6,-4), 斜率为 的直线的点斜式方程是
化为一般式,得4x+3y-12=0.
直线的方程中令y=0 即可得x的值.
解:把直线的一般式方程化为斜截
因此,直线的斜率 9 它 在y轴上的截距是3.
在直线的方程x-2y+6=0 中,令y=0, 得x=-6,
即直线l 在x轴上的截
例6把直线的一般式方程x-2y+6=0 化为斜截式,求出直线的斜率以
及它在x轴与y轴上的截距,并画出图形.
分析:求直线l 在x轴上的截距,即求直线l 与x轴交点的横坐标,只要在
距是 - 6 .
则直线l与x轴、y 轴的交点分别为A(-6,0),B(0,3),
过A,B两点作直线,就得直线l(如图).
●
·结合例6,我们可以从几何角度看一个二元一次方程 ,即一个二元一次方程表示一条直线.
·在代数中,我们研究了二元一次方程的解.因为二 元一次方程的每一组解都可以看成平面直角坐标系中
一个点的坐标,所以这个方程的全 笛卡儿,法国 就是坐标满足二元一次方程的全体数学家,解析几何 的集合组成一条直线. 创始人之一.
·平面直角坐标系是把二元一次方程和且线状系起米
的桥梁,这是笛卡儿的伟大贡献.在平面直角坐标系 中,任意一个二元一次方程是直角坐标平面上一条确 定的直线;反之,直角坐标平面上的任意一条直线可 以用一个确定的二元一次方程表示.
x+y—1=Q
(2)直线2x—y—2=0 绕它与y轴的交点A按逆时针方向 旋转90所得的直线方程是
A.x—2y+4=0 B.x+2y-4=0
C.x—2y—4=0 D.x+2y+4=0
(1)根据下列各条件写出直线的方程,并化成一般
式.
①斜率是 ,且经过点A(8, 一6)的直线方程为
x+2y+4
②在x轴和y轴上的截距分别是
2x—y—3=0
和一3的直线方程为
的直线方程为
③ 经 过 点P (3,—2),P (5,—4)
方法 一 ∵l′与 l垂直,
∴I的斜率 又l'过点(-1,3),
∴由点斜式可得方程为
即4x-3y+13=0.
方 法 二 由l′与1垂直,可设l' 的方程为4x-3y+n =0.
将(-1,3)代入上式得n=13.
∴所求直线的方程为4x-3y+13
=0.
(3)已知直线l的方程为3x+4y—12=0, 求满足下列
条件的直线l′的方程:
①过点(—1,3), ;②过点(一1,3),且与l垂直.
即3x+4y-9=
方 法 二 由l′与1平行,可设 l′的方程为3x+4y+m=0.
将点(-1,3)代入上式得m=-9. ∴所求直线的方程为3x+4y-9
行,I的斜率为
又∵l′过 点 (
为
∴
方法一 的 可化
∴由点斜式知方程为
=0.
事
反思感悟
过一点与已知直线平行(垂直)的直线方程的求法
①由已知直线求出斜率,再利用平行(垂直)的直 线斜率之间的关系确定所求直线的斜率,由点斜 式写方程并化成一般式.
②可利用如下待定系数法:与直线A x+By+C=
0(A,B 不同时为0)平行的直线方程可设为Ax+By +C =0 (C ≠C), 再由直线所过的点确定C ;
与直线Ax+By+C=0(A,B 不同时为0)垂直的直
线方程可设为Bx—Ay+C =0 , 再由直线所过的 点确定C .
反思感悟
③过定点P(x ,y )直线可表示为
y-y =k(x-x ) 或x=x
直线ax+y+a+2=0 过定点(-1,-2)
直线5ax-5y-a+3=0 过定点(1
3
例 设直线l的方程为(m —2m—3)x—(2m +m—1)y
+6—2m=0.
(1)已知直线l在x轴上的截距为一3,求m的值;
(2)已知直线l的斜率为1,求m 的值.
解
由题意知m -2m-3≠0,即m≠3且m≠-1, 令y=0,得
得 或m=3(舍去).
由直线化为斜截式方程
得
则
得m= 2或m=-1 (舍去).
∴m=-2.
一
解
由题意知,2m +m-1≠0, 即m m≠-1.
(2)已知直线l的斜率为1,求m 的值.
含参直线方程的研究策略
(1)若方程Ax+By+C=0 表示直线,则需满足A,
B不同时为0.
(2)令x=0 可得在y轴上的截距.令y=0 可得在x轴 上的截距.若确定直线斜率存在,可将一般式化 为斜截式.
(3)解分式方程要注意验根.
反思感悟
C.xl≠1 D.m≠1, ,m≠0
解析因为方程(2m +m—3)x+(m —m)y-4m+1=0 表示一条直
线,所以2m +m—3=0,m —m=0 不能同时成立,解得m≠1.
(2)若直线l:ax+y -2=0 在x轴 和y轴上的截距相等,
则a=1
跟踪训练2(1)若方程(2m +m-3)x+(m -m)y-4m+
1=0表示 一 条直线,则实数m 满 足
答案
A.m≠0
思考:直线 l:A x+B y+C =0,l :A x+B y+C =0
试讨论:(1)l //l 的条件是什么
(2)l ⊥l 的条件是什么
0n{AG-AG=0或
(2).I ⊥l A A +BB =0
0或AG-AG=0
3).1,l 相交
A
A
AG
A B
(
(
4).1,l 重合
位置 关系 直线 方程
=0
=0
重 合
平 行
日 ≠0
垂 直 一 」
A A 十 B B =0
相 交
A D A,B ≠0
【两条直线的几种位置关系】
跟踪训 1.判断下列各对直线是平行还是垂直,并说明
理由.
(1)l :3x+5y-6=0,L :6x+10y+3=0; I //l .
(2)l :3x—6y+14=0,l :2x+y—2=0;
l ⊥l .
2. 已知直线l :3x+(m+1)y -6=0,l :mx+2y-
(m+2)=0, 分别求满足下列条件的m 的值.
(1)l ⊥l ; (2)l //l .
2. 已知直线l :3x+(m+1)y -6=0,l :mx+2y-
(m+2)=0, 分别求满足下列条件的m 的值.
(1)l ⊥l ; (2)l //l .
解∵ ⊥ ,∴3×m+(m+1)×2=0,
解 ∵l //l ,∴3×2=m×(m+1),
∴m=—3 或m=2,
当m=—3 时,l //l ;
当m=2 时,l 与l 重合,不符合题意,舍去.
∴m=—3.
利用A B -A B =0 求出m值再检验
3.已知直线l :x+(a+1)y-2+a=0和
l :2ax+4y+16=0, 若l Ill , 求 a的值。
a=1
利用AB -A B =0 求出a 值再检验
4.已知直线l :ax+(a+1)y-a=0和l : (a+2)x+2(a+1)y-4=0,若 l //l , 求a 的值. a=-1
课堂
小结
1.知识清单:
(1)直线的一般式方程.
(2)直线五种形式方程的互化.
(3)利用直线方程判定直线的平行与垂直.
2.方法归纳:分类讨论法、化归转化.
3.常见误区:忽视直线斜率不存在的情况;忽视两直线
重合的情况.
探究与发现 方向向量与直线的参数方程
除了直线的点斜式、斜截式、两点式、截距式、 一般式方 程外,还有一种形式的直线方程与向量有紧密的联系,它 由一个定点和这条直线的方向向量唯一确定,与直线的点 斜式方程本质上是一致的.
如 图 1 , 设 直 线l 经过点P (xo,yo),v=
(m,n) 是它的一个方向向量,P(x,y) 是直线 l 上的任意一点,则向量P P 与v 共线.根据向量
共线的充要条件,存在唯一的实数t, 使P P
tv,即 (x—xo,y—yo)=t(m,n),
所 以
①
①
在①中,实数t 是对应点P 的参变数,简称参数.
由上可知,对于直线l 上的任意一点P(x,y), 存在唯一实数t 使①成立;
反之,对于参数t 的每一个确定的值,由①可以确定直线l 上的一个点 P(x,y). 我们把①称为直线的参数方程.
如果直线l 与坐标轴不垂直,那么 mn≠0, 由①可得
从运动学角度看,P P=tv(t>0) 可以看成质点P 从 点P。出发,以
速度v=(m,n) 作匀速直线运动,经过时间t 后的位移,因此,质点P 的 运动轨迹是射线P M. 类似地,你能刻画射线P N 吗 由以上讨论,你能
说说方程①的运动学意义吗
m n r
这样就得到直线l 的点斜式方程.
经过点P (xo,y ) ,倾斜角为α的直线l 的参数方程为
(t 为参数) ②
从另外一个角度思考,因为直线l 经过点P (xo,y ), 且它的一个方
向向量为v=(m,n), 所以直线l 的斜率 事 所以直线l 的方程为
已知直线的倾斜角α,则可以取 m=cosa,n =sina
中 ,(m,n) 的几何意义是什么
想一想,直线的参数方
你能说说t的几何意义吗
当P P与v同向时,t取正数;
当P P与v反 向 时 ,t 取负数;
当点P与P 重合时,t=0.
而且。=t1则
直线的参数方程中参数t 的 几何意义是:
t 表示参数t 对应的点P到 定 点P 的 距 离 。
M
P(x,y)
0
P (xo,yo)
结合P P=tv, 当 v=(cos a,sin α)时
名 称 几 何 条 件 方程
局限性
点斜式 点P (x ,y )和斜率k y-y =k(x-x,)
不垂直于x
轴
斜截式 斜率k,y轴上的纵截距b 12— r⊥ y-N1U
不垂直于x
轴
两点式 点P(x,y)和点P (x,y
不垂直于x轴
和y轴
截距式 在x轴上的截距a 在y轴上的截距b
不垂直于x、y轴的直
不过原点的直线
复习回顾
直线方程的四种形式:
载
直线与二元一次方程是否都有这种关系呢
下面我们探讨这个问题.
观察直线的点斜式、斜截式、两点式、截距式方程,我 们发现,它们都是关于x,y 的二元一次方程。比如:
y-y =k(x-x )—
y=kx+b —
y-y =x-x
y -y X -X (y -Y )x+(x -x )y+x(y -y )+y(x -x )=0
→kx+(-1)y+y -kx
kx+(-1)y+b=0
=0
1.掌握直 线的一般 式方程. 2.理解关于x,y的二 元一次方程Ax+By 十C=0(A,B不同时
3.会进行直线方
程的五种形式之 间的转化。
为0)都表示直线.
首称
(1).平面直角坐标系中的每一条直线都可以用 一个关于x,y的二元一次方程表示吗
(2).每一个关于x,y的二元一次方程都表示一
条直线吗
先看问题(1),任意一条直线l,在其上任取一点P(x ,y ), 当直线的斜率为k时(此时直线的倾斜角α≠90°),
其方程为 y-y =k(x-x ),
这是关于x,y 的二元一次方程.
当直线的斜率不存在,即直线l的倾斜角α=90°,直线的方程为
x-x =0
上述方程可以认为是关于x,y 的二元一次方程,因为此时方程中y的系数
为0. 方程y-y。=k(x-x ) 和x-x =0 都是二元一次方程,
因此平面直角坐标系中的任意一条直线都可以用一个
关于x,y 的二元一次方程表示.
反之,对于任意一个二元一次方程Ax+By+C=0(A,B 不同时为0),
如果能把它化为直线方程的某种形式,那么我们就可以断定它表示 一条直线.
当B≠0 时,方程Ax+By+C=0 可变形为 9
它表示过点 ,斜率为 的直线.
当B=0 时,A≠0, 方程Ax+By+C=0 可变形为
它表示过点 且垂直于x轴的直线
·由上可知,关于x,y的二元一次方程都表示一条直线.
直线的一般式方程:
我们把关于x,y的二元一次方程
Ax+By+C=0
(其中A,B不同时为0)叫做直线的一般式方程,简称一般式(general form)
注意:对于直线方程的一般式, 一般作如下约定:
1)x的系数为正;
2)x,y的系数及常数项一般不出现分数;
3)按含x项,含y项、常数项顺序排列. 4)没有特别说明,都要写成一般式
在方程Ax+By+C=0 中 ,A,B,C 为何值时,方
程表示的直线:
(1)平行于x轴;(2)平行于y轴;(3)与x轴重合;
(4)与y轴重合;(5)过原点;
(1)A=0,B≠0,C≠0
(2)B=0,A≠0,C≠0 (3)A=0,B≠0, C=0
X (4)B=0,A≠0, C=0
(5)C=0,A、B 不同时为0
例5已知直线经过点A(6,-4),斜率为 ,求直线的点斜式和一般式方程.
解:经过点A(6,-4), 斜率为 的直线的点斜式方程是
化为一般式,得4x+3y-12=0.
直线的方程中令y=0 即可得x的值.
解:把直线的一般式方程化为斜截
因此,直线的斜率 9 它 在y轴上的截距是3.
在直线的方程x-2y+6=0 中,令y=0, 得x=-6,
即直线l 在x轴上的截
例6把直线的一般式方程x-2y+6=0 化为斜截式,求出直线的斜率以
及它在x轴与y轴上的截距,并画出图形.
分析:求直线l 在x轴上的截距,即求直线l 与x轴交点的横坐标,只要在
距是 - 6 .
则直线l与x轴、y 轴的交点分别为A(-6,0),B(0,3),
过A,B两点作直线,就得直线l(如图).
●
·结合例6,我们可以从几何角度看一个二元一次方程 ,即一个二元一次方程表示一条直线.
·在代数中,我们研究了二元一次方程的解.因为二 元一次方程的每一组解都可以看成平面直角坐标系中
一个点的坐标,所以这个方程的全 笛卡儿,法国 就是坐标满足二元一次方程的全体数学家,解析几何 的集合组成一条直线. 创始人之一.
·平面直角坐标系是把二元一次方程和且线状系起米
的桥梁,这是笛卡儿的伟大贡献.在平面直角坐标系 中,任意一个二元一次方程是直角坐标平面上一条确 定的直线;反之,直角坐标平面上的任意一条直线可 以用一个确定的二元一次方程表示.
x+y—1=Q
(2)直线2x—y—2=0 绕它与y轴的交点A按逆时针方向 旋转90所得的直线方程是
A.x—2y+4=0 B.x+2y-4=0
C.x—2y—4=0 D.x+2y+4=0
(1)根据下列各条件写出直线的方程,并化成一般
式.
①斜率是 ,且经过点A(8, 一6)的直线方程为
x+2y+4
②在x轴和y轴上的截距分别是
2x—y—3=0
和一3的直线方程为
的直线方程为
③ 经 过 点P (3,—2),P (5,—4)
方法 一 ∵l′与 l垂直,
∴I的斜率 又l'过点(-1,3),
∴由点斜式可得方程为
即4x-3y+13=0.
方 法 二 由l′与1垂直,可设l' 的方程为4x-3y+n =0.
将(-1,3)代入上式得n=13.
∴所求直线的方程为4x-3y+13
=0.
(3)已知直线l的方程为3x+4y—12=0, 求满足下列
条件的直线l′的方程:
①过点(—1,3), ;②过点(一1,3),且与l垂直.
即3x+4y-9=
方 法 二 由l′与1平行,可设 l′的方程为3x+4y+m=0.
将点(-1,3)代入上式得m=-9. ∴所求直线的方程为3x+4y-9
行,I的斜率为
又∵l′过 点 (
为
∴
方法一 的 可化
∴由点斜式知方程为
=0.
事
反思感悟
过一点与已知直线平行(垂直)的直线方程的求法
①由已知直线求出斜率,再利用平行(垂直)的直 线斜率之间的关系确定所求直线的斜率,由点斜 式写方程并化成一般式.
②可利用如下待定系数法:与直线A x+By+C=
0(A,B 不同时为0)平行的直线方程可设为Ax+By +C =0 (C ≠C), 再由直线所过的点确定C ;
与直线Ax+By+C=0(A,B 不同时为0)垂直的直
线方程可设为Bx—Ay+C =0 , 再由直线所过的 点确定C .
反思感悟
③过定点P(x ,y )直线可表示为
y-y =k(x-x ) 或x=x
直线ax+y+a+2=0 过定点(-1,-2)
直线5ax-5y-a+3=0 过定点(1
3
例 设直线l的方程为(m —2m—3)x—(2m +m—1)y
+6—2m=0.
(1)已知直线l在x轴上的截距为一3,求m的值;
(2)已知直线l的斜率为1,求m 的值.
解
由题意知m -2m-3≠0,即m≠3且m≠-1, 令y=0,得
得 或m=3(舍去).
由直线化为斜截式方程
得
则
得m= 2或m=-1 (舍去).
∴m=-2.
一
解
由题意知,2m +m-1≠0, 即m m≠-1.
(2)已知直线l的斜率为1,求m 的值.
含参直线方程的研究策略
(1)若方程Ax+By+C=0 表示直线,则需满足A,
B不同时为0.
(2)令x=0 可得在y轴上的截距.令y=0 可得在x轴 上的截距.若确定直线斜率存在,可将一般式化 为斜截式.
(3)解分式方程要注意验根.
反思感悟
C.xl≠1 D.m≠1, ,m≠0
解析因为方程(2m +m—3)x+(m —m)y-4m+1=0 表示一条直
线,所以2m +m—3=0,m —m=0 不能同时成立,解得m≠1.
(2)若直线l:ax+y -2=0 在x轴 和y轴上的截距相等,
则a=1
跟踪训练2(1)若方程(2m +m-3)x+(m -m)y-4m+
1=0表示 一 条直线,则实数m 满 足
答案
A.m≠0
思考:直线 l:A x+B y+C =0,l :A x+B y+C =0
试讨论:(1)l //l 的条件是什么
(2)l ⊥l 的条件是什么
0n{AG-AG=0或
(2).I ⊥l A A +BB =0
0或AG-AG=0
3).1,l 相交
A
A
AG
A B
(
(
4).1,l 重合
位置 关系 直线 方程
=0
=0
重 合
平 行
日 ≠0
垂 直 一 」
A A 十 B B =0
相 交
A D A,B ≠0
【两条直线的几种位置关系】
跟踪训 1.判断下列各对直线是平行还是垂直,并说明
理由.
(1)l :3x+5y-6=0,L :6x+10y+3=0; I //l .
(2)l :3x—6y+14=0,l :2x+y—2=0;
l ⊥l .
2. 已知直线l :3x+(m+1)y -6=0,l :mx+2y-
(m+2)=0, 分别求满足下列条件的m 的值.
(1)l ⊥l ; (2)l //l .
2. 已知直线l :3x+(m+1)y -6=0,l :mx+2y-
(m+2)=0, 分别求满足下列条件的m 的值.
(1)l ⊥l ; (2)l //l .
解∵ ⊥ ,∴3×m+(m+1)×2=0,
解 ∵l //l ,∴3×2=m×(m+1),
∴m=—3 或m=2,
当m=—3 时,l //l ;
当m=2 时,l 与l 重合,不符合题意,舍去.
∴m=—3.
利用A B -A B =0 求出m值再检验
3.已知直线l :x+(a+1)y-2+a=0和
l :2ax+4y+16=0, 若l Ill , 求 a的值。
a=1
利用AB -A B =0 求出a 值再检验
4.已知直线l :ax+(a+1)y-a=0和l : (a+2)x+2(a+1)y-4=0,若 l //l , 求a 的值. a=-1
课堂
小结
1.知识清单:
(1)直线的一般式方程.
(2)直线五种形式方程的互化.
(3)利用直线方程判定直线的平行与垂直.
2.方法归纳:分类讨论法、化归转化.
3.常见误区:忽视直线斜率不存在的情况;忽视两直线
重合的情况.
探究与发现 方向向量与直线的参数方程
除了直线的点斜式、斜截式、两点式、截距式、 一般式方 程外,还有一种形式的直线方程与向量有紧密的联系,它 由一个定点和这条直线的方向向量唯一确定,与直线的点 斜式方程本质上是一致的.
如 图 1 , 设 直 线l 经过点P (xo,yo),v=
(m,n) 是它的一个方向向量,P(x,y) 是直线 l 上的任意一点,则向量P P 与v 共线.根据向量
共线的充要条件,存在唯一的实数t, 使P P
tv,即 (x—xo,y—yo)=t(m,n),
所 以
①
①
在①中,实数t 是对应点P 的参变数,简称参数.
由上可知,对于直线l 上的任意一点P(x,y), 存在唯一实数t 使①成立;
反之,对于参数t 的每一个确定的值,由①可以确定直线l 上的一个点 P(x,y). 我们把①称为直线的参数方程.
如果直线l 与坐标轴不垂直,那么 mn≠0, 由①可得
从运动学角度看,P P=tv(t>0) 可以看成质点P 从 点P。出发,以
速度v=(m,n) 作匀速直线运动,经过时间t 后的位移,因此,质点P 的 运动轨迹是射线P M. 类似地,你能刻画射线P N 吗 由以上讨论,你能
说说方程①的运动学意义吗
m n r
这样就得到直线l 的点斜式方程.
经过点P (xo,y ) ,倾斜角为α的直线l 的参数方程为
(t 为参数) ②
从另外一个角度思考,因为直线l 经过点P (xo,y ), 且它的一个方
向向量为v=(m,n), 所以直线l 的斜率 事 所以直线l 的方程为
已知直线的倾斜角α,则可以取 m=cosa,n =sina
中 ,(m,n) 的几何意义是什么
想一想,直线的参数方
你能说说t的几何意义吗
当P P与v同向时,t取正数;
当P P与v反 向 时 ,t 取负数;
当点P与P 重合时,t=0.
而且。=t1则
直线的参数方程中参数t 的 几何意义是:
t 表示参数t 对应的点P到 定 点P 的 距 离 。
M
P(x,y)
0
P (xo,yo)
结合P P=tv, 当 v=(cos a,sin α)时
