2.3.3点到直线的距离公式 课件(共24张PPT)—— 高中数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.3.3点到直线的距离公式 课件(共24张PPT)—— 高中数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 22:03:19 | ||
图片预览






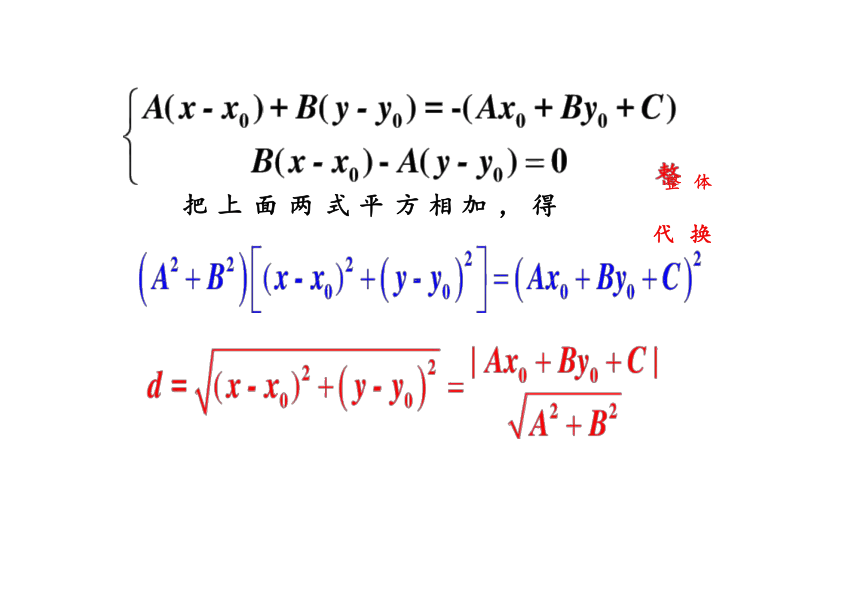

文档简介
(共24张PPT)
距离问题是几何学的基本问题之一,上节课
我们学习了两点间的距离公式,知道两点间 的距离可以由两点坐标表示.
在平面直角坐标系中,我们用坐标描述点, 用方程刻画直线,当点与直线的位置确定后, 点到直线的距离可以由点的坐标与直线的方 程确定,如何确定呢
1.经历用坐标法、向量 法推导点到直线的距离 公式的运算过程,发展
2.掌握点到直线 的距离公式,并 能灵活应用.
数学运算与逻辑推理素
首标
养.
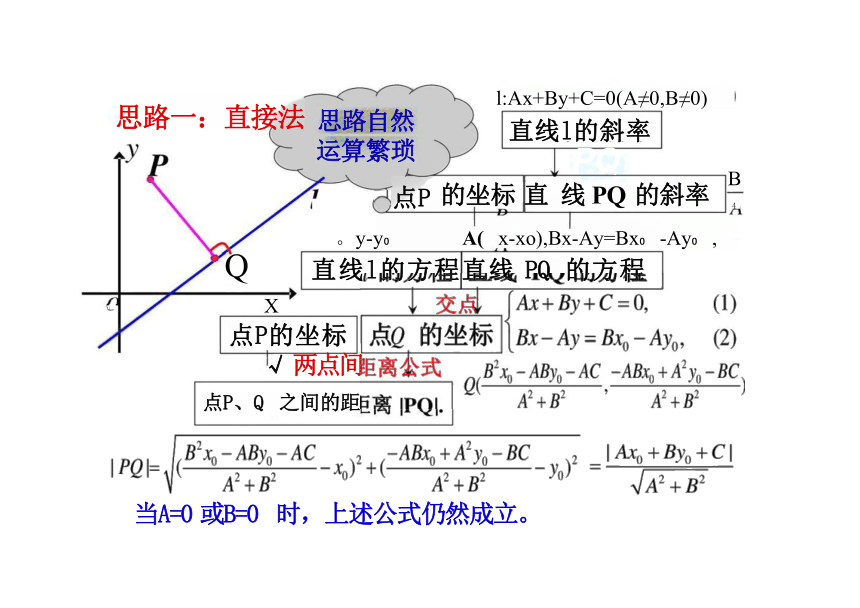
问 题 如图,已知点P(x,y ),直 线l:Ax+By+C=0(A≠0,B≠0)
如何求点P 到直线 l 的距离
点P 到直线l的距离的定义
点P到直线的距离,是指
从点P到直线的垂线段PQ
的长度,其中Q 是垂足.
如何求|PQ| 你有那些想法
[直接法]求出点Q坐标,利用两点间距离公式
[ 间 接 法 ] 构 造直角三角形 采用等面积法
[ 向 量 法]向量是解决距离的有力工具,能否用向量法
。y-y A( x-xo),Bx-Ay=Bx -Ay ,
Q 直线l的方程直线 PQ 的方程
X
点P的坐标
√ 两点间
点P、Q 之间的距
思路一:直接法 思路自然 运算繁琐
l 点P
PQ
的坐标 直 线 PQ 的斜率
l:Ax+By+C=0(A≠0,B≠0)
直线l的斜率
当A=0 或B=0 时,上述公式仍然成立。
B
4
U
上述推导过程思路自然,但运算较繁,反思求解 过程,你能发现引起复’杂运算的原因吗
O
能否不求点 Q 的坐标
上述推导过程思路自然,但运算较繁,反思求 解过程,你能发现引起复杂运算的原因吗
解方程组
不妨设 Q(x,y),则 IPQI=√(x-x) +(y-y)
能否从方程组中直接求出x-x,y-y
设而
不求
4
整 体
把 上 面 两 式 平 方 相 加 , 得
代 换
思路二:间接法
l:Ax+By+C=0(A≠0,B≠0)
求出点R的坐标 求出点S的坐标
求出 |PR| Ax +By +( 求出|PS| Ax 十 y
A B
B
0
利用勾股定理求出|RSI
IPQIIRS=IPRI IPSI
等面积法求出|PQ
当A=0或B=0 时,上述公式仍然成立。
By 十 C
Q
Ax + X
B
S
思路三:向量法
向量是解决空间距离、角度问题的有力工具,能否用向量 方法求点到直线的距离呢
点P 与直线l 上任一点所成向量与向量PQ
有何关系
向量 PQ是 PM , … PM,, 在PQ
上的投影向量.
在直线l 上任取一点M,|PQI 与 PM 有
何关系 设 n是直线PQ 的方向向量,
求出直线l与y轴的交点M 的坐标
l的一个方向
向量(B,—A).
求出PM| 求出直线l的垂直向量n
C n=(A,B)
求出PM在n 上的投影向量PQ 长
n
0
MWC
(0,B
思路三:向量投影法l:Ax+By+C= 0
Q
X
-X0,-B-yo)
Ax +By +CI
√A +B
(1)利用公式时直线的方程必须是一般式;
(2)分子含有绝对值;
(3)若直线方程为Ax+By+C=0,则当A=0或B=0时
公式也成立,但由于直线是特殊直线(与坐标轴垂直), 故也可用数形结合求解.
点P(xo,yo)到直线l:Ax+By+C=0(A,B 不全为0)
点到直线的距高:
注意点:
d=
的距离:
例5:求点 p(-1,2) 到直线 l:3x=2 的距离.
解:直线的方程可化为一般式:3x-2=0
思考:还有 其他解法吗
,直线3x=2平行于y轴,
3.已知点P(-1,2) 到直线l:4x-3y+C=0 的距离为1,求C的值 13.已知点A(a,6) 到直线3x—4y=2 的距离d 分别为下列各值:
(1)d=4;(2)d> 4, 求 a 的取值范围.
1 4 . 已 知A(—3,—4),B(6,3) 两 点 到 直 线l:
ax+y+1=0 的 距 离 相 等 , 求a 的 值 .
跟踪训练1 1. 求原点到下列直线的距离:
(1)l:3x+2y—26=0; (2)l:x=y. 2.求下列点到直线的距离:
l:3x+4y+3=0;
l:√3x+y-√3=0; l:4.x+3y=0.
(1)A(—2,3),
(2)B(1,0),
(3)C(1,—2),
AB=√(3-1) +(1-3) =2√2 y 3 A(1,3)
边AB 所在直线的方程为
2
即x+y-4=0 h
点C(-1,0)到直线l 的距离为
C(-1,0
还有其他
方法吗
例 6 已 知 点A(1,3),B(3,1),C(-1,0), 求 △ABC 的面积 .
解:设边AB 上的高为h,则
例6已知点A(1,3),B(3,1),C(-1,0),求三角形ABC 的面 积.
解法二:
SAABc=SACp-SABCD
割补
点到直线距离公式的 综合应用
当直线的斜率不存在时,直线的方程为x=2, 符合题意; 当直线的斜率存在时,设直线的方程为y+1=k(x -2),
即kx -y-2k-1=0, 由点到直线的距离公式 解得 所以直线的方程为3x-4y -10=0. 故直线的方程为x=2 或3x-4y-10=0.
例已知点P(2,—1),求过点P且与原点距离为2的直线l
的方程.
延伸探究求过点P(2,—1)且与原点距离最大的直线
l的方程,最大距离是多少
解:设原点为0,连接OP,
易知过点P且与原点距离最大的
直线是过点P 且与PO 垂直的
由1⊥OP, 得k kop=-1 所
所以直线的方程为y+1=2(x-2), 即 2x-y-5=0,
即直线2x -y-5=0是过点P且与原点距离最大的直
线 ,
最大距离
反思感悟
解决有限制条件的点到直线的距离的问题需注 意分类讨论,利用数形结合的思想,直观地观 察一些量的变化,从而达到解决问题的目的.
跟踪训 已知直线l 过点M(—1,2), 且点A(2,3),B(—4,5)
到的距离相等,求直线l的方程.
你有哪些办法解决此题
解
方法一 当过点M(-1,2)的直线的斜率不存在时, 直线的方程为x=-1
此时点A(2,3)与点B(-4,5)到直线的距离相等, 故x=-1 满足题意;
当过点M(-1,2) 的直线的斜率存在时,
设的方程为y-2=k(x+1),
即kx-y+k+2=0.
由点A(2,3)与B(-4,5)到直线的距离相等,
中
综上所述,直线的方程为x=-1 或x+3y-5=0 .
即 x+3y-5=0.
解得
此时直线l的方程为 9
即x+3y-5=0.
当过AB 的中点(-1,4)时,直线的方程为x=-1. 综上所述,直线的方程为x=-1 或x+3y-5=0.
方法二由题意得l//AB 或过线段AB 的中点.
当l//AB时,设直线AB 的斜率为kAB,直线的斜率为k ,
课堂
小结
1.知识清单:
(1)点到直线的距离公式的推导过程;
(2)点到直线的距离公式d=
(3)公式的应用.
2.方法归纳:公式法、数形结合.
3.常见误区:设直线方程忽略斜率是否存在.
距离问题是几何学的基本问题之一,上节课
我们学习了两点间的距离公式,知道两点间 的距离可以由两点坐标表示.
在平面直角坐标系中,我们用坐标描述点, 用方程刻画直线,当点与直线的位置确定后, 点到直线的距离可以由点的坐标与直线的方 程确定,如何确定呢
1.经历用坐标法、向量 法推导点到直线的距离 公式的运算过程,发展
2.掌握点到直线 的距离公式,并 能灵活应用.
数学运算与逻辑推理素
首标
养.
问 题 如图,已知点P(x,y ),直 线l:Ax+By+C=0(A≠0,B≠0)
如何求点P 到直线 l 的距离
点P 到直线l的距离的定义
点P到直线的距离,是指
从点P到直线的垂线段PQ
的长度,其中Q 是垂足.
如何求|PQ| 你有那些想法
[直接法]求出点Q坐标,利用两点间距离公式
[ 间 接 法 ] 构 造直角三角形 采用等面积法
[ 向 量 法]向量是解决距离的有力工具,能否用向量法
。y-y A( x-xo),Bx-Ay=Bx -Ay ,
Q 直线l的方程直线 PQ 的方程
X
点P的坐标
√ 两点间
点P、Q 之间的距
思路一:直接法 思路自然 运算繁琐
l 点P
PQ
的坐标 直 线 PQ 的斜率
l:Ax+By+C=0(A≠0,B≠0)
直线l的斜率
当A=0 或B=0 时,上述公式仍然成立。
B
4
U
上述推导过程思路自然,但运算较繁,反思求解 过程,你能发现引起复’杂运算的原因吗
O
能否不求点 Q 的坐标
上述推导过程思路自然,但运算较繁,反思求 解过程,你能发现引起复杂运算的原因吗
解方程组
不妨设 Q(x,y),则 IPQI=√(x-x) +(y-y)
能否从方程组中直接求出x-x,y-y
设而
不求
4
整 体
把 上 面 两 式 平 方 相 加 , 得
代 换
思路二:间接法
l:Ax+By+C=0(A≠0,B≠0)
求出点R的坐标 求出点S的坐标
求出 |PR| Ax +By +( 求出|PS| Ax 十 y
A B
B
0
利用勾股定理求出|RSI
IPQIIRS=IPRI IPSI
等面积法求出|PQ
当A=0或B=0 时,上述公式仍然成立。
By 十 C
Q
Ax + X
B
S
思路三:向量法
向量是解决空间距离、角度问题的有力工具,能否用向量 方法求点到直线的距离呢
点P 与直线l 上任一点所成向量与向量PQ
有何关系
向量 PQ是 PM , … PM,, 在PQ
上的投影向量.
在直线l 上任取一点M,|PQI 与 PM 有
何关系 设 n是直线PQ 的方向向量,
求出直线l与y轴的交点M 的坐标
l的一个方向
向量(B,—A).
求出PM| 求出直线l的垂直向量n
C n=(A,B)
求出PM在n 上的投影向量PQ 长
n
0
MWC
(0,B
思路三:向量投影法l:Ax+By+C= 0
Q
X
-X0,-B-yo)
Ax +By +CI
√A +B
(1)利用公式时直线的方程必须是一般式;
(2)分子含有绝对值;
(3)若直线方程为Ax+By+C=0,则当A=0或B=0时
公式也成立,但由于直线是特殊直线(与坐标轴垂直), 故也可用数形结合求解.
点P(xo,yo)到直线l:Ax+By+C=0(A,B 不全为0)
点到直线的距高:
注意点:
d=
的距离:
例5:求点 p(-1,2) 到直线 l:3x=2 的距离.
解:直线的方程可化为一般式:3x-2=0
思考:还有 其他解法吗
,直线3x=2平行于y轴,
3.已知点P(-1,2) 到直线l:4x-3y+C=0 的距离为1,求C的值 13.已知点A(a,6) 到直线3x—4y=2 的距离d 分别为下列各值:
(1)d=4;(2)d> 4, 求 a 的取值范围.
1 4 . 已 知A(—3,—4),B(6,3) 两 点 到 直 线l:
ax+y+1=0 的 距 离 相 等 , 求a 的 值 .
跟踪训练1 1. 求原点到下列直线的距离:
(1)l:3x+2y—26=0; (2)l:x=y. 2.求下列点到直线的距离:
l:3x+4y+3=0;
l:√3x+y-√3=0; l:4.x+3y=0.
(1)A(—2,3),
(2)B(1,0),
(3)C(1,—2),
AB=√(3-1) +(1-3) =2√2 y 3 A(1,3)
边AB 所在直线的方程为
2
即x+y-4=0 h
点C(-1,0)到直线l 的距离为
C(-1,0
还有其他
方法吗
例 6 已 知 点A(1,3),B(3,1),C(-1,0), 求 △ABC 的面积 .
解:设边AB 上的高为h,则
例6已知点A(1,3),B(3,1),C(-1,0),求三角形ABC 的面 积.
解法二:
SAABc=SACp-SABCD
割补
点到直线距离公式的 综合应用
当直线的斜率不存在时,直线的方程为x=2, 符合题意; 当直线的斜率存在时,设直线的方程为y+1=k(x -2),
即kx -y-2k-1=0, 由点到直线的距离公式 解得 所以直线的方程为3x-4y -10=0. 故直线的方程为x=2 或3x-4y-10=0.
例已知点P(2,—1),求过点P且与原点距离为2的直线l
的方程.
延伸探究求过点P(2,—1)且与原点距离最大的直线
l的方程,最大距离是多少
解:设原点为0,连接OP,
易知过点P且与原点距离最大的
直线是过点P 且与PO 垂直的
由1⊥OP, 得k kop=-1 所
所以直线的方程为y+1=2(x-2), 即 2x-y-5=0,
即直线2x -y-5=0是过点P且与原点距离最大的直
线 ,
最大距离
反思感悟
解决有限制条件的点到直线的距离的问题需注 意分类讨论,利用数形结合的思想,直观地观 察一些量的变化,从而达到解决问题的目的.
跟踪训 已知直线l 过点M(—1,2), 且点A(2,3),B(—4,5)
到的距离相等,求直线l的方程.
你有哪些办法解决此题
解
方法一 当过点M(-1,2)的直线的斜率不存在时, 直线的方程为x=-1
此时点A(2,3)与点B(-4,5)到直线的距离相等, 故x=-1 满足题意;
当过点M(-1,2) 的直线的斜率存在时,
设的方程为y-2=k(x+1),
即kx-y+k+2=0.
由点A(2,3)与B(-4,5)到直线的距离相等,
中
综上所述,直线的方程为x=-1 或x+3y-5=0 .
即 x+3y-5=0.
解得
此时直线l的方程为 9
即x+3y-5=0.
当过AB 的中点(-1,4)时,直线的方程为x=-1. 综上所述,直线的方程为x=-1 或x+3y-5=0.
方法二由题意得l//AB 或过线段AB 的中点.
当l//AB时,设直线AB 的斜率为kAB,直线的斜率为k ,
课堂
小结
1.知识清单:
(1)点到直线的距离公式的推导过程;
(2)点到直线的距离公式d=
(3)公式的应用.
2.方法归纳:公式法、数形结合.
3.常见误区:设直线方程忽略斜率是否存在.
