2.5.1 直线与圆的位置关系 课件(共30张PPT)—— 高中数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.5.1 直线与圆的位置关系 课件(共30张PPT)—— 高中数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 22:11:21 | ||
图片预览











文档简介
(共30张PPT)
第二章直线和圆的方程
2.5.1直线与圆的位置关系
学习目标
1.能根据给定直线、圆的方程,判断直线与圆的位置关系.
2.能用直线和圆的方程解决一些简单的数学问题和实际问题. 3.逐步理解用代数方法处理几何问题的基本思想和方法.
(1)直线与圆相交,有两个公共点 d(2)直线与圆相切,只有一个公共点 d=r;
(3)直线与圆相离,没有公共点 d>r.
直线与圆的位置关系
例题巩
例1已知直线l:3x+y-6=0 和圆心为C 的 圆x +y -2y-4 =0, 判 断
直 线l 与 圆C 的位置关系;如果相交,求直线l 被 圆C 所截得的弦长.
解法1:联立直线l与圆C 的方程,得
消去y, 得x -3x+2=0, 解 得x=2,x =1.
所以,直线l 与圆C 相交,有两个公共点.
把x=2,x = 1分别代入方程①,得y =0,y =3.
所以,直线1与圆C 的两个交点是A(2,0),B(1,3).
因此I ABI=√ 1-2) +(3-0) =√ 10.
圆心C(0,1)到直线l 的距离
所以,直线l 与圆C 相交,有两个公共点.
如图,由垂径定理,得|AB|=2 √r -d = √ 10.
解 法 2 :圆 C 的方程x +y -2y -4=0 可化为x +(y-1) =5,
因此圆心 C 的坐标为(0,1),半径为√5,
在平面直角坐标系中,要判断直线l:Ax+By+C=0 与圆
C:(x-a) +(y-b) =r 的位置关系,可以联立它们的方程,
通过判定方程组 的解的个数,得出直线
与圆的公共点的个数,进而判断直线与圆的位置关系.若相交, 可由方程组解得两交点坐标,利用两点间的距离公式求得弦长.
例2过点P(2,1)作圆0 :x +y = 1的切线l, 求切线l 的方程.
解 法 1 :设切线1的斜率为 k,
则切线l的方程为y-1=k(x-2), 即kx-y+1-2k=0.
由圆心(0,0)到切线l 的距离等于圆的半径1,得
解得k=0 或
因此,所求切线1的方程为y=1, 或 4x-3y-5=0.
因为方程①只有一个解,
所以△=4k (1-2k) -16k(k +1)(k-1)=0,解得k=0 或 ■
所以,所求切线l的方程为y=1, 或 4x-3y-5=0.
解法2:设切线1的斜率为k,则切线1的方程为y-1=k(x-2).
消元,得(k +1)x +(2k-4k )x+4k -4k=0.①
因为直线1与圆相切,所以方程
只有一组解.
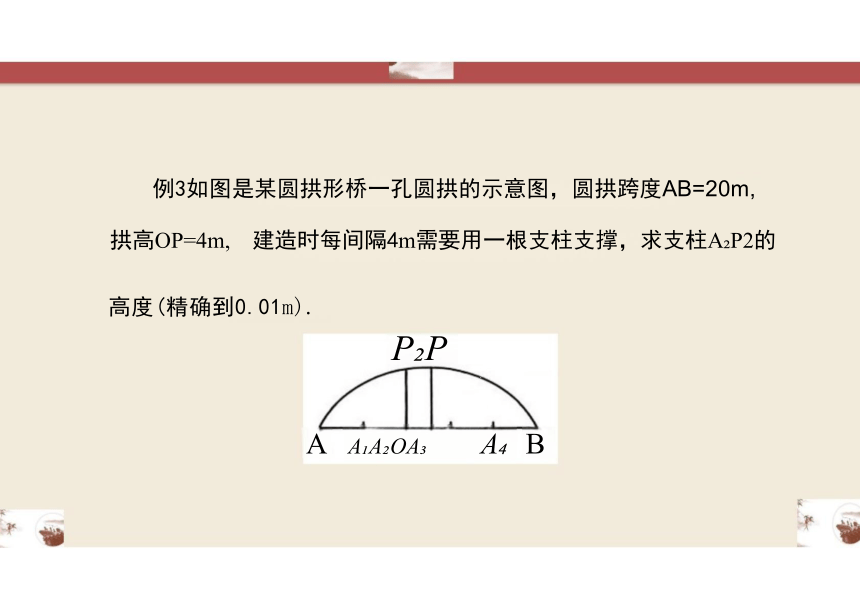
例3如图是某圆拱形桥一孔圆拱的示意图,圆拱跨度AB=20m,
拱高OP=4m, 建造时每间隔4m需要用一根支柱支撑,求支柱A P2的
高度(精确到0.01m).
P P
A A A OA A B
因为P,B 两点都在圆上,代入得 ,解得b=-10.5,r =14.5 .
所以圆的方程是x +(y+10.5) =14.5 .
把点P 的横坐标x=-2 代入圆的方程,得(-2) +(y+10.5) =14.5 , 即 y+10.5= √ 14.5 -(-2) (P 的纵坐标y>0,平方根取正值).
所以y= √ 14.5 -(-2) -10.5≈14.36-10.5=3.86(m),
故支柱A P2的高度约为3.86m.
解:建立如图所示的直角坐标系,使线段AB所在直线为x 轴,0为坐标
原点,圆心在y轴上.
由题意,点P,B 的坐标分别为(0,4),(10,0).
设圆心坐标是(0,b), 圆的半径是r, 则圆的方程是x +(y-b) =r .A
y
P P
A
A 0 A A B X
例4一个小岛的周围有环岛暗礁,暗礁分布在以小岛中心为圆心,
半径为20 km的圆形区域内. 已知小岛中心位于轮船正西40 km 处,港 口位于小岛中心正北30 km 处.如果轮船沿直线返港,那么它是否会有 触礁危险
受暗礁影响的圆形区域的边缘所对应的圆的方程为x +y =4.
轮船航线所在直线l的方程为 ,即3x+4y-12=0.
yA
港口
联立直线l与 圆O 的 方 程 ,
0 轮船x
消去y, 得25x -72x+80=0.
解 :以小岛的中心为原点O, 东西方向为x 轴,建立如图所示的直角坐标系.取10 km
为单位长度,则港口所在位置的坐标为(0,3),轮船所在位置的坐标为(4,0).
由△=(-72) -4×25×80< 0,可知方程组无解.
所以直线1与圆O 相离,轮船沿直线返港不会有触礁危险.
用坐标法解决平面几何问题的“三步曲”
第一步:建立适当的平面直角坐标系,用坐标和方程表示问 题中的几何要素,如点、直线、圆,把平面几何问题转化为 代数问题;
第二步:通过代数运算,解决代数问题;
第三步:把代数运算的结果“翻译”成几何结论.
解析:直线y=kx+1 恒过定点(0,1),由定点(0,1)在圆x +y =2 内,知直线y=kx+1
与圆 x +y =2 一定相交.又直线y=kx+1 不过圆心(0,0),所以位置关系是相交但直 线不过圆心,故选C.
课堂小练
1.对任意的实数k, 直 线y=kx+1 与圆x +y =2 的位置关系一定是 (
A.相离
C. 相交但直线不过圆心
B.相切
D. 相交且直线过圆心
2.若直线l 与圆x +y -4x=0相切于点P(1,√3),则直线l 的方程为(D
解析:由题意,得点P 在圆上,且点P 与圆心(2,0)的连线的斜率是-√3,则切线1
的斜率是 ,则切线方程为
B.x+√3y-4=0
D.x-√3y+2=0
即为x- √3y+2=0.故选D.
3.若直线3x+4y+m=0 与圆x +y -2x+4y+1=0 没有公共点,则实数m 的
取值范围是(
A.-515
C.m<4 或m>13 D.4解析:圆 x +y -2x+4y+1=0
的圆心为(1,-2),半径为2,由题意得,圆心到
直线3x+4y+m=0 的距离
, ∴m<-5 或m>15. 故选B.
4.若直线x-y=2 被 圆(x-a) +y =4 所截得的弦长为2 √ 2,则实数a 的值为(A)
A.0 或 4 B.0或3 C.-2 或 6 D.-1或 √3
,所以|a-2|=2, 解得
解析:由圆的方程,可知圆心坐标为(a,0), 半径r=2. 又直线被圆截得的弦长为2 √2,
所以圆心到直线的距离
a=4 或a=0. 故选A.
5.一束光线从点 A(-2,3) 射出,经x 轴反射后与圆x +y -6x-4y+12=0 相切,
则反射光线所在直线的斜率为(C )
或 日 或 C. 或 口 或
A
解析:圆的方程可化为(x-3) +(y-2) =1, 易 知A(-2,3) 关于x轴对称的点为
A'(-2,-3),如图所示,易知反射光线所在直线的斜率存在,设为k,其方程为
y+3=k(x+2), 即 kx-y+2k-3=0, 依题意得,圆心到反射光线所在直线的距离
化简得12k -25k+12=0, 解 得
y
A 3
2
-2 3 x
A' -3
或 .故选C.
6. (多选)已知圆M:(x-a) +(y-a-1) =1(a∈ R) , 则ABD
A.圆 M 可能过原点
B.圆 心M 在直线x-y-1=0 上
C. 圆 M 与直线x-y-1=0 相切
D.圆M被直线x-y=0 所戴得的弦长为 √2
oooo
解析:圆M:(x-a) +(y-a-1) =1(a∈R), 圆心为M(a,a+1), M
过原点,则(0-a) +(0-a-1) =1, 解 得a=0 或a=-1, 故 A 正确;
因为a-(a+1)+1=0, 所以圆心M 在直线x-y+1=0 上,故B 正确;
圆心到直线x-y-1=0 的距离 ,故圆M 与直线x-y-1=0
相离,故C 错误;
圆心到直线x-y=0 的距离 ,所以圆M 被直线x-y=0 截得的
, 故D 正确.故选ABD.
7.过点(2,3)且与圆(x-1) +y =1相切的直线的方程为4 x-3y+1=0 或 x=2
解析:易知点(2,3)在圆外,当切线的斜率存在时,设圆的切线方程为y=k(x-2)+3, 由圆心(1,0)到切线的距离等于半径,得 所以切线方程为4x-3y+1=0.
当切线的斜率不存在时,切线方程为x=2. 综上,所求直线的方程为4x-3y+1=0 或x=2.
8.如图所示是一座圆拱桥,当水面在如图所示的位置时,拱桥顶部离水面2m, 水面宽12m, 若水面下降1m, 则水面的宽为 m.
2 m
解 析 :如图,建立平面直角坐标系,设初始水面在AB处,则由已知得A(6,-2), 设
圆 C 的半径长为r(r>0), 则 C(0,-r), 故 圆C 的方程为x +(y+r) =r , 将A(6,-2) 代入,得r=10, 所以圆C 的方程为x +(y+10) =100.① 当水面下降1m 到A'B′时,
设A'(x ,-3)(x >0). 将A'(x,-3) 代入①式,得x =√51, 所以水面下降1m 后,水面
宽为2 √51 m. yA
B A
B' A'
C
0 X
9.已知圆C:(x-1) +(y-2) =25, 直 线l:(2m+1)x+(m+1)y-7m-4=0(m∈ R).
(1)求证:不论m 取什么实数,直线l 与圆恒有两个不同的交点;
(2)若直线l 被圆C 截得的弦长最小,求此时l 的方程.
解 析:(1)将直线l的方程改写成(x+y-4)+ m(2x+y-7)=0,
因 为m∈R, 所 以 解 得x=3,y=1,
可知直线l恒过定点A(3,1),
因为圆心C(1,2), 半 径r=5, 易得 |AC|=√5<5=r,
因此点A 必在圆C 内,故直线1与圆恒有两个不同的交点.
(2)由图形位置关系可知,当弦长最小时,必有l⊥AC,
因 为 则k,=2,
从 而 得 , 故 直 线l 的方程为2x-y-5=0.
10.已知点M(3,1), 直 线ax-y+4=0 及圆(x-1) +(y-2) =4.
(1)求过点M的圆的切线方程;
(2)若直线ax-y+4=0 与圆相切,求a 的值;
(3)若直线ax-y+4=0 与圆相交于A,B 两点,且弦AB的长为2 √ 3,求a 的值.
解 析 :(1)由题意得,圆心C(1,2), 半 径r=2.
当直线的斜率不存在时,方程为x=3.
由圆心C(1,2)到直线x=3 的距离d =3-1=2=r 知,此时,直线与圆相切.
当直线的斜率存在时,设方程为y-1=k(x-3), 即 kx-y+1-3k=0.
由题意知圆心到直线的距离 ,解得
∴方程为3x-4y-5=0.
故过点M的圆的切线方程为x=3 或3x-4y-5=0
(2)由题意得,圆心到直线ax-y+4=0 的距离为
解得a=0 或
(3)∵圆心到直线ax-y+4=0 的距离为
解得
小结:
回顾一下本节课学习了哪些新知识呢
直线与圆的位置关系及应用.
第二章直线和圆的方程
2.5.1直线与圆的位置关系
学习目标
1.能根据给定直线、圆的方程,判断直线与圆的位置关系.
2.能用直线和圆的方程解决一些简单的数学问题和实际问题. 3.逐步理解用代数方法处理几何问题的基本思想和方法.
(1)直线与圆相交,有两个公共点 d
(3)直线与圆相离,没有公共点 d>r.
直线与圆的位置关系
例题巩
例1已知直线l:3x+y-6=0 和圆心为C 的 圆x +y -2y-4 =0, 判 断
直 线l 与 圆C 的位置关系;如果相交,求直线l 被 圆C 所截得的弦长.
解法1:联立直线l与圆C 的方程,得
消去y, 得x -3x+2=0, 解 得x=2,x =1.
所以,直线l 与圆C 相交,有两个公共点.
把x=2,x = 1分别代入方程①,得y =0,y =3.
所以,直线1与圆C 的两个交点是A(2,0),B(1,3).
因此I ABI=√ 1-2) +(3-0) =√ 10.
圆心C(0,1)到直线l 的距离
所以,直线l 与圆C 相交,有两个公共点.
如图,由垂径定理,得|AB|=2 √r -d = √ 10.
解 法 2 :圆 C 的方程x +y -2y -4=0 可化为x +(y-1) =5,
因此圆心 C 的坐标为(0,1),半径为√5,
在平面直角坐标系中,要判断直线l:Ax+By+C=0 与圆
C:(x-a) +(y-b) =r 的位置关系,可以联立它们的方程,
通过判定方程组 的解的个数,得出直线
与圆的公共点的个数,进而判断直线与圆的位置关系.若相交, 可由方程组解得两交点坐标,利用两点间的距离公式求得弦长.
例2过点P(2,1)作圆0 :x +y = 1的切线l, 求切线l 的方程.
解 法 1 :设切线1的斜率为 k,
则切线l的方程为y-1=k(x-2), 即kx-y+1-2k=0.
由圆心(0,0)到切线l 的距离等于圆的半径1,得
解得k=0 或
因此,所求切线1的方程为y=1, 或 4x-3y-5=0.
因为方程①只有一个解,
所以△=4k (1-2k) -16k(k +1)(k-1)=0,解得k=0 或 ■
所以,所求切线l的方程为y=1, 或 4x-3y-5=0.
解法2:设切线1的斜率为k,则切线1的方程为y-1=k(x-2).
消元,得(k +1)x +(2k-4k )x+4k -4k=0.①
因为直线1与圆相切,所以方程
只有一组解.
例3如图是某圆拱形桥一孔圆拱的示意图,圆拱跨度AB=20m,
拱高OP=4m, 建造时每间隔4m需要用一根支柱支撑,求支柱A P2的
高度(精确到0.01m).
P P
A A A OA A B
因为P,B 两点都在圆上,代入得 ,解得b=-10.5,r =14.5 .
所以圆的方程是x +(y+10.5) =14.5 .
把点P 的横坐标x=-2 代入圆的方程,得(-2) +(y+10.5) =14.5 , 即 y+10.5= √ 14.5 -(-2) (P 的纵坐标y>0,平方根取正值).
所以y= √ 14.5 -(-2) -10.5≈14.36-10.5=3.86(m),
故支柱A P2的高度约为3.86m.
解:建立如图所示的直角坐标系,使线段AB所在直线为x 轴,0为坐标
原点,圆心在y轴上.
由题意,点P,B 的坐标分别为(0,4),(10,0).
设圆心坐标是(0,b), 圆的半径是r, 则圆的方程是x +(y-b) =r .A
y
P P
A
A 0 A A B X
例4一个小岛的周围有环岛暗礁,暗礁分布在以小岛中心为圆心,
半径为20 km的圆形区域内. 已知小岛中心位于轮船正西40 km 处,港 口位于小岛中心正北30 km 处.如果轮船沿直线返港,那么它是否会有 触礁危险
受暗礁影响的圆形区域的边缘所对应的圆的方程为x +y =4.
轮船航线所在直线l的方程为 ,即3x+4y-12=0.
yA
港口
联立直线l与 圆O 的 方 程 ,
0 轮船x
消去y, 得25x -72x+80=0.
解 :以小岛的中心为原点O, 东西方向为x 轴,建立如图所示的直角坐标系.取10 km
为单位长度,则港口所在位置的坐标为(0,3),轮船所在位置的坐标为(4,0).
由△=(-72) -4×25×80< 0,可知方程组无解.
所以直线1与圆O 相离,轮船沿直线返港不会有触礁危险.
用坐标法解决平面几何问题的“三步曲”
第一步:建立适当的平面直角坐标系,用坐标和方程表示问 题中的几何要素,如点、直线、圆,把平面几何问题转化为 代数问题;
第二步:通过代数运算,解决代数问题;
第三步:把代数运算的结果“翻译”成几何结论.
解析:直线y=kx+1 恒过定点(0,1),由定点(0,1)在圆x +y =2 内,知直线y=kx+1
与圆 x +y =2 一定相交.又直线y=kx+1 不过圆心(0,0),所以位置关系是相交但直 线不过圆心,故选C.
课堂小练
1.对任意的实数k, 直 线y=kx+1 与圆x +y =2 的位置关系一定是 (
A.相离
C. 相交但直线不过圆心
B.相切
D. 相交且直线过圆心
2.若直线l 与圆x +y -4x=0相切于点P(1,√3),则直线l 的方程为(D
解析:由题意,得点P 在圆上,且点P 与圆心(2,0)的连线的斜率是-√3,则切线1
的斜率是 ,则切线方程为
B.x+√3y-4=0
D.x-√3y+2=0
即为x- √3y+2=0.故选D.
3.若直线3x+4y+m=0 与圆x +y -2x+4y+1=0 没有公共点,则实数m 的
取值范围是(
A.-5
C.m<4 或m>13 D.4
的圆心为(1,-2),半径为2,由题意得,圆心到
直线3x+4y+m=0 的距离
, ∴m<-5 或m>15. 故选B.
4.若直线x-y=2 被 圆(x-a) +y =4 所截得的弦长为2 √ 2,则实数a 的值为(A)
A.0 或 4 B.0或3 C.-2 或 6 D.-1或 √3
,所以|a-2|=2, 解得
解析:由圆的方程,可知圆心坐标为(a,0), 半径r=2. 又直线被圆截得的弦长为2 √2,
所以圆心到直线的距离
a=4 或a=0. 故选A.
5.一束光线从点 A(-2,3) 射出,经x 轴反射后与圆x +y -6x-4y+12=0 相切,
则反射光线所在直线的斜率为(C )
或 日 或 C. 或 口 或
A
解析:圆的方程可化为(x-3) +(y-2) =1, 易 知A(-2,3) 关于x轴对称的点为
A'(-2,-3),如图所示,易知反射光线所在直线的斜率存在,设为k,其方程为
y+3=k(x+2), 即 kx-y+2k-3=0, 依题意得,圆心到反射光线所在直线的距离
化简得12k -25k+12=0, 解 得
y
A 3
2
-2 3 x
A' -3
或 .故选C.
6. (多选)已知圆M:(x-a) +(y-a-1) =1(a∈ R) , 则ABD
A.圆 M 可能过原点
B.圆 心M 在直线x-y-1=0 上
C. 圆 M 与直线x-y-1=0 相切
D.圆M被直线x-y=0 所戴得的弦长为 √2
oooo
解析:圆M:(x-a) +(y-a-1) =1(a∈R), 圆心为M(a,a+1), M
过原点,则(0-a) +(0-a-1) =1, 解 得a=0 或a=-1, 故 A 正确;
因为a-(a+1)+1=0, 所以圆心M 在直线x-y+1=0 上,故B 正确;
圆心到直线x-y-1=0 的距离 ,故圆M 与直线x-y-1=0
相离,故C 错误;
圆心到直线x-y=0 的距离 ,所以圆M 被直线x-y=0 截得的
, 故D 正确.故选ABD.
7.过点(2,3)且与圆(x-1) +y =1相切的直线的方程为4 x-3y+1=0 或 x=2
解析:易知点(2,3)在圆外,当切线的斜率存在时,设圆的切线方程为y=k(x-2)+3, 由圆心(1,0)到切线的距离等于半径,得 所以切线方程为4x-3y+1=0.
当切线的斜率不存在时,切线方程为x=2. 综上,所求直线的方程为4x-3y+1=0 或x=2.
8.如图所示是一座圆拱桥,当水面在如图所示的位置时,拱桥顶部离水面2m, 水面宽12m, 若水面下降1m, 则水面的宽为 m.
2 m
解 析 :如图,建立平面直角坐标系,设初始水面在AB处,则由已知得A(6,-2), 设
圆 C 的半径长为r(r>0), 则 C(0,-r), 故 圆C 的方程为x +(y+r) =r , 将A(6,-2) 代入,得r=10, 所以圆C 的方程为x +(y+10) =100.① 当水面下降1m 到A'B′时,
设A'(x ,-3)(x >0). 将A'(x,-3) 代入①式,得x =√51, 所以水面下降1m 后,水面
宽为2 √51 m. yA
B A
B' A'
C
0 X
9.已知圆C:(x-1) +(y-2) =25, 直 线l:(2m+1)x+(m+1)y-7m-4=0(m∈ R).
(1)求证:不论m 取什么实数,直线l 与圆恒有两个不同的交点;
(2)若直线l 被圆C 截得的弦长最小,求此时l 的方程.
解 析:(1)将直线l的方程改写成(x+y-4)+ m(2x+y-7)=0,
因 为m∈R, 所 以 解 得x=3,y=1,
可知直线l恒过定点A(3,1),
因为圆心C(1,2), 半 径r=5, 易得 |AC|=√5<5=r,
因此点A 必在圆C 内,故直线1与圆恒有两个不同的交点.
(2)由图形位置关系可知,当弦长最小时,必有l⊥AC,
因 为 则k,=2,
从 而 得 , 故 直 线l 的方程为2x-y-5=0.
10.已知点M(3,1), 直 线ax-y+4=0 及圆(x-1) +(y-2) =4.
(1)求过点M的圆的切线方程;
(2)若直线ax-y+4=0 与圆相切,求a 的值;
(3)若直线ax-y+4=0 与圆相交于A,B 两点,且弦AB的长为2 √ 3,求a 的值.
解 析 :(1)由题意得,圆心C(1,2), 半 径r=2.
当直线的斜率不存在时,方程为x=3.
由圆心C(1,2)到直线x=3 的距离d =3-1=2=r 知,此时,直线与圆相切.
当直线的斜率存在时,设方程为y-1=k(x-3), 即 kx-y+1-3k=0.
由题意知圆心到直线的距离 ,解得
∴方程为3x-4y-5=0.
故过点M的圆的切线方程为x=3 或3x-4y-5=0
(2)由题意得,圆心到直线ax-y+4=0 的距离为
解得a=0 或
(3)∵圆心到直线ax-y+4=0 的距离为
解得
小结:
回顾一下本节课学习了哪些新知识呢
直线与圆的位置关系及应用.
