2.5.2 椭圆的几何性质(1) 课件(共28张PPT)-人教B版高中数学选择性必修第一册-教案课件习题试卷-高中数学人教版B版选择性必修第一册
文档属性
| 名称 | 2.5.2 椭圆的几何性质(1) 课件(共28张PPT)-人教B版高中数学选择性必修第一册-教案课件习题试卷-高中数学人教版B版选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 22:08:17 | ||
图片预览







文档简介
(共28张PPT)
人教2019B版选择性必修第一册
第二章平面解析几何
2.5.2椭圆的几何性质(1)
1.掌握椭圆的几何性质,掌握a,b,c,e的几何意义及a,b,c,e 之间的相互关系
2.尝试利用椭圆的方程研究椭圆的几何性质.
3.尝试利用椭圆的知识解决简单的实际问题.
已知椭圆C的方程 ,根据这个方程完成下列任务:
(1)已观察方程中与是否有取值范围,由此指出椭圆C在
平面直角坐标系中的位置特征;
(2)指出椭圆C 是否关于x轴、 y 轴、原点对称;
(3)指出椭圆C与坐标轴是否有交点,如果有,求出交点坐标.
y=1
-1
x=2
下面我们由椭圆的方程来研究椭圆具有的几何性质
4y
o
x=-2
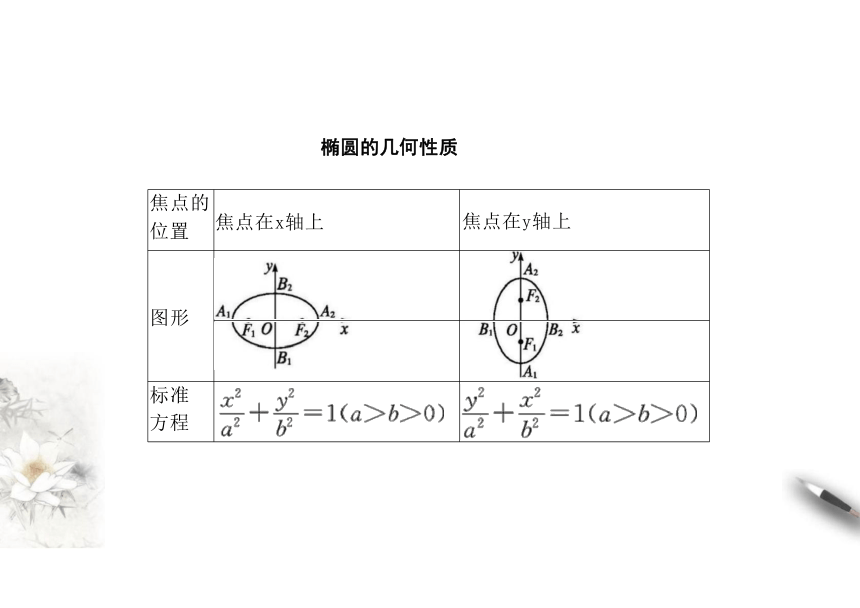
焦点的 位置 焦点在x轴上
焦点在y轴上
图形
标准 方程
椭圆的几何性质
焦点的 位置 焦点在x轴上
焦点在y轴上
范围 -a≤x≤a且-b≤y≤b
-b≤x≤b且-a≤y≤a
顶点 B (0,-b),B (0,b)
B (-b,0),B (b,0)
轴长 长轴长为2a,短轴长为2b
焦点 (c,0)
o
焦距 2c
对称性 C ( 0 , 1 ) , 其 中C U 2
离心率 a
解析:∵a =4+2 =8,∴a=2 √2.. 故选C.
答案:C
的一个焦点为(2,0),则C 的离心率为( )
C 口
1.已知椭圆
A
B
2.判断
(1)椭 的长轴长是a. ( )
(2)若椭圆的对称轴为坐标轴,长轴长与短轴长分别为10,8,则椭圆的
方 程 ( )
(3)设F 为 椭 的一个焦点,M 为其上任一点,则
|MF| 的最大值为a+c(c 为椭圆的半焦距). ( )
答案:(1)×(2)×(3) √
(1)根据椭圆离心率的定义判断椭圆离心率的取值范围;
(2)猜想椭圆离心率的大小与椭圆的形状有什么联系,并尝试证明。
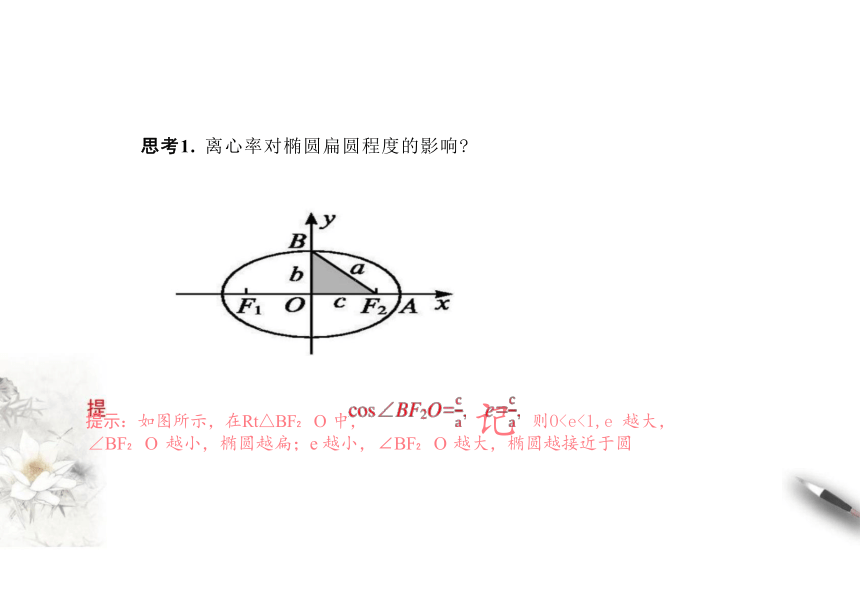
提示:如图所示,在Rt△BF O 中, 记 则O思考1. 离心率对椭圆扁圆程度的影响
垂
解:(1)由椭圆 可得其半长轴长为10,半短轴长为8,焦 点坐标为(6,0),(-6,0),离心率
(2)椭圆 .性质如下:
①范围: -8≤x≤8 且-10≤y≤10;② 对称性:关于x 轴、y 轴、原点对 称;③顶点:长轴端点(0,10),(0,-10),短轴端点(-8,0),(8,0);④焦
点:(0,6),(0,-6);⑤离心率:
例 1已知椭圆 ,设椭圆C 与椭圆C 的长轴
长、短轴长分别相等,且椭圆C 的焦点在y轴上.
(1)求椭圆C 的半长轴长、半短轴长、焦点坐标及离心率; (2)写出椭圆C 的方程,并研究其性质.
讨论椭圆的几何性质时, 一定要将方程化为标准方程,标准方
程能将参数的几何意义凸显出来,另外要抓住椭圆中a -b =c 这一 核心关系式.
解:由已知
因为0所以椭圆的焦点在x 轴上,并且半长轴长
半短轴长 半焦距
所以椭圆的长轴长
焦点坐标为
顶点坐标为 手
离心率
跟踪训练1求椭圆m x +4m y =1(m>0)的长轴长、短轴长、焦点坐标、顶点坐标和离心率.
,短轴长
事
例2 椭 圆 (a>b>0) 的两焦点为F ,F , 以F F 为边作正三角形,若椭圆恰好平分
正三角形的另两条边,则椭圆的离心率为
方法二:注意到焦点三角形NF F 中,∠NF F =30°,∠NF F =60°
∠F NF =90°, 则由离心率的焦点三角形公式,可得
解析:方法一:如图,∵△DF F 为正三角形,N 为 DF 的中点, ∴F NLF N.∵|NF I=|OF I=c,
由椭圆的定义可知|NF I+|NF I=2a, ∴√3c+c=2a,∴
答案: √3-1
变式1若例2改为如下:椭圆 的两焦点F ,F , 以
F F 为底边作等腰直角三角形,其三角形顶点恰好落在椭圆的顶点
处,则椭圆的离心率为
解析:根据等腰直角三角形的特征可知a +a =4c , 即
答案
例 3 已知椭圆 分别是椭圆的左、右焦点,椭 圆上总存在点P 使 得PF ⊥PF , 则椭圆的离心率的取值范围
为
解析:由PF ⊥PF , 知△F PF 是直角三角形,
所以|OP|=c≥b, 即c ≥a -c , 所以a≤√2c.
因为 ,0答案
求椭圆离心率的值或取值范围的常用方法
(1)直接法:若已知a,c, 可直接利用 求解.若已知a,b( 或b,c) 可借助
于 a =b +c 求 出c( 或a),再代入公式 求解.
(2)几何法:若借助数形结合,可挖掘涉及几何图形的性质,再借助
a =b +c ,找 到a 与 c 的关系或求出a 与 c,代 入 即可得到.
(3)方程法:若a,c的值不可求,则可根据条件建立关于a,b,c的关系式,借助于
a =b +c ,转化为关于a,c的齐次方程(或不等式),再将方程(或不等式)两边同
除 以a的最高次幂,得到关于e的方程(或不等式),即可求得e的值(或取值范围).
跟踪训练2(1)已知椭圆 过点(1, √2),其离心率的取 值范围是 ,则椭圆短轴长的最大值是( )
A.4 B.3 C.√ 11 D.2√3
(2)设F ,F 分别是椭圆 的左、右焦点,P 为直线 上一点,△F PF 是底角为30°的等腰三角形,则E 的离心率 为
解析:(1)由题意,可得 ,即
因为a =b +c ,所 离心率的取值范围是 解得 ,所以椭圆短轴长的最大值是
√ 11.
(2)由题意,知∠F F P=∠F PF =30°,
∴∠PF x=60°∴ ∵|F F |=2c,|F F I=|PF ],∴3a-2c=2c,
答案:(1)C (2)
(3)已知椭圆 的左、右焦点分别为F ,F , 右顶点 为A, 上顶点为B, 若椭圆C 的中心到直线AB 的 距 离 ,求椭
圆 C 的离心率.
解:由题意知A(a,0),B(0,b),
从而直线AB的 方 程 ,即bx+ay-ab=0, 又 F| F |=2c,∴
∵b =a -c ,∴3a -7a c +2c =0,
解 得a =2c 或 3a =c (舍去),
:
·
例4 .神舟五号飞船成功完成了第一次载人航天飞行,实现了中国人民的航天梦想.某段时间飞
船在太空中运行的轨道是一个椭圆,地心为椭圆的一个焦点,如右图所示.假设航天员到地球表 面的最近距离为d ,最远距离为d ,地球的半径为R,我们想象存在一个镜像地球,其中心在神舟 飞船运行轨道的另外一个焦点上,上面发射某种神秘信号,需要飞行中的航天员中转后地球上 的人才能接收到,则传送神秘信号的最短距离为( )
A.d +d +R B.d -d +2R C.d +d -2R D.d +d
解析:设椭圆的方程为 半焦距为c, 两焦点分别为F ,F , 飞行中的航天员为点P,
由已知可得
则 2a=d +d +2R,
故传送神秘信号的最短距离为|PF | +|PF |-2R=2a-2R=d +d .
答案:D
1.已知点(3,2)在椭 上,则( )
A.点(-3,-2)不在椭圆上
B.点(3,-2)不在椭圆上
解析:由椭圆以坐标轴为对称轴,以原点为对称中心可知,点(-3,2)在椭圆上,故选C.
答案:C
C.点(-3,2)在椭圆上
D.无法判断点(-3,-2),(3,-2),(-3,2)是否在椭圆上
2.设AB 是椭圆 (a>b>0) 的长轴,若把线段AB分为100等份,过每个分点
作AB的垂线,分别交椭圆的上半部分于点P ,P ,...,P 9,F 为椭圆的左焦点,则
|F A|+|F P I+|F P I+...+|F P99I+|F B| 的值是( )
A.98a B.99a C.100a D.101a
解析:由椭圆的定义及其对称性可知
|F P I+|F P 9I=|F P I+|F P 8I=...=|F P 9I+|F P I=|F A|+|F B|=2a,
|F P I=a, 故结果应为50×2a+|F P I=101a.
答案:D
解析:不妨设椭圆的左、右焦点分别为F ,F ,B为椭圆的 上顶点.依题意可知,△BF F 是正三角形.
∵在Rt△OBF 中,IOF I=c,
|BF I=a,∠OF B=60°,
即椭圆的离心率 故选A.
3.若椭圆的两个焦点与短轴的一个端点构成一个正三角形,则该椭圆的离心率为( )
答案:A
A
B
口
C
则四边形B F B F 的面积为
解析:根据题意,设四边形B F B F 的面积为S, 椭圆的标准方程为 ,其中a=√3,b= √2, 则c=√3-2=1,
则F (-1,0),F (1,0),B (0,√2),B (0,-√2),
即|OF I=|OF I=1,|OB I=|OB I=√2,
左、右焦点分别为F ,F , 上、下顶点分别为B ,B
答案:2 √2
4.已知椭
解析:因为两个椭圆的扁平程度相同,所以椭圆的离心率相同,
所以小椭
圆的长轴长为20 cm.
答案:20
5.万众瞩目的北京冬奥会将于2022年2月4日正式开幕,继2008年北
京奥运会之后,国家体育场(又名鸟巢)将再次承办奥运会开幕式.在 手工课上,王老师带领同学们一起制作了一个近似鸟巢的金属模型, 其俯视图可近似看成是两个大小不同、扁平程度相同的椭圆.已知 大椭圆的长轴长为40 cm,短轴长为20 cm, 小椭圆的短轴长为10 cm, 则小椭圆的长轴长为 cm.
。
解:椭圆方程可化为
:
∴a =m, 7 由 ∴椭圆的标准方程为 .. ∴a=1, 2,短轴长为1;两焦点坐标分别为 为(-1,0),(1,0), ,
得 , ∴m=1.
重 ∴椭圆的长轴长为
;四个顶点坐标分别
6.已知椭圆x +(m+3)y =m(m>0)的离心率
长轴长、短轴长、焦点坐标、顶点坐标.
求m 的值及椭圆的
··
1
5
范围
对称性
顶点
离心率
椭圆的几何性质
应 用
人教2019B版选择性必修第一册
第二章平面解析几何
2.5.2椭圆的几何性质(1)
1.掌握椭圆的几何性质,掌握a,b,c,e的几何意义及a,b,c,e 之间的相互关系
2.尝试利用椭圆的方程研究椭圆的几何性质.
3.尝试利用椭圆的知识解决简单的实际问题.
已知椭圆C的方程 ,根据这个方程完成下列任务:
(1)已观察方程中与是否有取值范围,由此指出椭圆C在
平面直角坐标系中的位置特征;
(2)指出椭圆C 是否关于x轴、 y 轴、原点对称;
(3)指出椭圆C与坐标轴是否有交点,如果有,求出交点坐标.
y=1
-1
x=2
下面我们由椭圆的方程来研究椭圆具有的几何性质
4y
o
x=-2
焦点的 位置 焦点在x轴上
焦点在y轴上
图形
标准 方程
椭圆的几何性质
焦点的 位置 焦点在x轴上
焦点在y轴上
范围 -a≤x≤a且-b≤y≤b
-b≤x≤b且-a≤y≤a
顶点 B (0,-b),B (0,b)
B (-b,0),B (b,0)
轴长 长轴长为2a,短轴长为2b
焦点 (c,0)
o
焦距 2c
对称性 C ( 0 , 1 ) , 其 中C U 2
离心率 a
解析:∵a =4+2 =8,∴a=2 √2.. 故选C.
答案:C
的一个焦点为(2,0),则C 的离心率为( )
C 口
1.已知椭圆
A
B
2.判断
(1)椭 的长轴长是a. ( )
(2)若椭圆的对称轴为坐标轴,长轴长与短轴长分别为10,8,则椭圆的
方 程 ( )
(3)设F 为 椭 的一个焦点,M 为其上任一点,则
|MF| 的最大值为a+c(c 为椭圆的半焦距). ( )
答案:(1)×(2)×(3) √
(1)根据椭圆离心率的定义判断椭圆离心率的取值范围;
(2)猜想椭圆离心率的大小与椭圆的形状有什么联系,并尝试证明。
提示:如图所示,在Rt△BF O 中, 记 则O
垂
解:(1)由椭圆 可得其半长轴长为10,半短轴长为8,焦 点坐标为(6,0),(-6,0),离心率
(2)椭圆 .性质如下:
①范围: -8≤x≤8 且-10≤y≤10;② 对称性:关于x 轴、y 轴、原点对 称;③顶点:长轴端点(0,10),(0,-10),短轴端点(-8,0),(8,0);④焦
点:(0,6),(0,-6);⑤离心率:
例 1已知椭圆 ,设椭圆C 与椭圆C 的长轴
长、短轴长分别相等,且椭圆C 的焦点在y轴上.
(1)求椭圆C 的半长轴长、半短轴长、焦点坐标及离心率; (2)写出椭圆C 的方程,并研究其性质.
讨论椭圆的几何性质时, 一定要将方程化为标准方程,标准方
程能将参数的几何意义凸显出来,另外要抓住椭圆中a -b =c 这一 核心关系式.
解:由已知
因为0
半短轴长 半焦距
所以椭圆的长轴长
焦点坐标为
顶点坐标为 手
离心率
跟踪训练1求椭圆m x +4m y =1(m>0)的长轴长、短轴长、焦点坐标、顶点坐标和离心率.
,短轴长
事
例2 椭 圆 (a>b>0) 的两焦点为F ,F , 以F F 为边作正三角形,若椭圆恰好平分
正三角形的另两条边,则椭圆的离心率为
方法二:注意到焦点三角形NF F 中,∠NF F =30°,∠NF F =60°
∠F NF =90°, 则由离心率的焦点三角形公式,可得
解析:方法一:如图,∵△DF F 为正三角形,N 为 DF 的中点, ∴F NLF N.∵|NF I=|OF I=c,
由椭圆的定义可知|NF I+|NF I=2a, ∴√3c+c=2a,∴
答案: √3-1
变式1若例2改为如下:椭圆 的两焦点F ,F , 以
F F 为底边作等腰直角三角形,其三角形顶点恰好落在椭圆的顶点
处,则椭圆的离心率为
解析:根据等腰直角三角形的特征可知a +a =4c , 即
答案
例 3 已知椭圆 分别是椭圆的左、右焦点,椭 圆上总存在点P 使 得PF ⊥PF , 则椭圆的离心率的取值范围
为
解析:由PF ⊥PF , 知△F PF 是直角三角形,
所以|OP|=c≥b, 即c ≥a -c , 所以a≤√2c.
因为 ,0
求椭圆离心率的值或取值范围的常用方法
(1)直接法:若已知a,c, 可直接利用 求解.若已知a,b( 或b,c) 可借助
于 a =b +c 求 出c( 或a),再代入公式 求解.
(2)几何法:若借助数形结合,可挖掘涉及几何图形的性质,再借助
a =b +c ,找 到a 与 c 的关系或求出a 与 c,代 入 即可得到.
(3)方程法:若a,c的值不可求,则可根据条件建立关于a,b,c的关系式,借助于
a =b +c ,转化为关于a,c的齐次方程(或不等式),再将方程(或不等式)两边同
除 以a的最高次幂,得到关于e的方程(或不等式),即可求得e的值(或取值范围).
跟踪训练2(1)已知椭圆 过点(1, √2),其离心率的取 值范围是 ,则椭圆短轴长的最大值是( )
A.4 B.3 C.√ 11 D.2√3
(2)设F ,F 分别是椭圆 的左、右焦点,P 为直线 上一点,△F PF 是底角为30°的等腰三角形,则E 的离心率 为
解析:(1)由题意,可得 ,即
因为a =b +c ,所 离心率的取值范围是 解得 ,所以椭圆短轴长的最大值是
√ 11.
(2)由题意,知∠F F P=∠F PF =30°,
∴∠PF x=60°∴ ∵|F F |=2c,|F F I=|PF ],∴3a-2c=2c,
答案:(1)C (2)
(3)已知椭圆 的左、右焦点分别为F ,F , 右顶点 为A, 上顶点为B, 若椭圆C 的中心到直线AB 的 距 离 ,求椭
圆 C 的离心率.
解:由题意知A(a,0),B(0,b),
从而直线AB的 方 程 ,即bx+ay-ab=0, 又 F| F |=2c,∴
∵b =a -c ,∴3a -7a c +2c =0,
解 得a =2c 或 3a =c (舍去),
:
·
例4 .神舟五号飞船成功完成了第一次载人航天飞行,实现了中国人民的航天梦想.某段时间飞
船在太空中运行的轨道是一个椭圆,地心为椭圆的一个焦点,如右图所示.假设航天员到地球表 面的最近距离为d ,最远距离为d ,地球的半径为R,我们想象存在一个镜像地球,其中心在神舟 飞船运行轨道的另外一个焦点上,上面发射某种神秘信号,需要飞行中的航天员中转后地球上 的人才能接收到,则传送神秘信号的最短距离为( )
A.d +d +R B.d -d +2R C.d +d -2R D.d +d
解析:设椭圆的方程为 半焦距为c, 两焦点分别为F ,F , 飞行中的航天员为点P,
由已知可得
则 2a=d +d +2R,
故传送神秘信号的最短距离为|PF | +|PF |-2R=2a-2R=d +d .
答案:D
1.已知点(3,2)在椭 上,则( )
A.点(-3,-2)不在椭圆上
B.点(3,-2)不在椭圆上
解析:由椭圆以坐标轴为对称轴,以原点为对称中心可知,点(-3,2)在椭圆上,故选C.
答案:C
C.点(-3,2)在椭圆上
D.无法判断点(-3,-2),(3,-2),(-3,2)是否在椭圆上
2.设AB 是椭圆 (a>b>0) 的长轴,若把线段AB分为100等份,过每个分点
作AB的垂线,分别交椭圆的上半部分于点P ,P ,...,P 9,F 为椭圆的左焦点,则
|F A|+|F P I+|F P I+...+|F P99I+|F B| 的值是( )
A.98a B.99a C.100a D.101a
解析:由椭圆的定义及其对称性可知
|F P I+|F P 9I=|F P I+|F P 8I=...=|F P 9I+|F P I=|F A|+|F B|=2a,
|F P I=a, 故结果应为50×2a+|F P I=101a.
答案:D
解析:不妨设椭圆的左、右焦点分别为F ,F ,B为椭圆的 上顶点.依题意可知,△BF F 是正三角形.
∵在Rt△OBF 中,IOF I=c,
|BF I=a,∠OF B=60°,
即椭圆的离心率 故选A.
3.若椭圆的两个焦点与短轴的一个端点构成一个正三角形,则该椭圆的离心率为( )
答案:A
A
B
口
C
则四边形B F B F 的面积为
解析:根据题意,设四边形B F B F 的面积为S, 椭圆的标准方程为 ,其中a=√3,b= √2, 则c=√3-2=1,
则F (-1,0),F (1,0),B (0,√2),B (0,-√2),
即|OF I=|OF I=1,|OB I=|OB I=√2,
左、右焦点分别为F ,F , 上、下顶点分别为B ,B
答案:2 √2
4.已知椭
解析:因为两个椭圆的扁平程度相同,所以椭圆的离心率相同,
所以小椭
圆的长轴长为20 cm.
答案:20
5.万众瞩目的北京冬奥会将于2022年2月4日正式开幕,继2008年北
京奥运会之后,国家体育场(又名鸟巢)将再次承办奥运会开幕式.在 手工课上,王老师带领同学们一起制作了一个近似鸟巢的金属模型, 其俯视图可近似看成是两个大小不同、扁平程度相同的椭圆.已知 大椭圆的长轴长为40 cm,短轴长为20 cm, 小椭圆的短轴长为10 cm, 则小椭圆的长轴长为 cm.
。
解:椭圆方程可化为
:
∴a =m, 7 由 ∴椭圆的标准方程为 .. ∴a=1, 2,短轴长为1;两焦点坐标分别为 为(-1,0),(1,0), ,
得 , ∴m=1.
重 ∴椭圆的长轴长为
;四个顶点坐标分别
6.已知椭圆x +(m+3)y =m(m>0)的离心率
长轴长、短轴长、焦点坐标、顶点坐标.
求m 的值及椭圆的
··
1
5
范围
对称性
顶点
离心率
椭圆的几何性质
应 用
