2.5.2 椭圆的几何性质(2) 课件(共39张PPT)-人教B版高中数学选择性必修第一册-教案课件习题试卷-高中数学人教版B版选择性必修第一册
文档属性
| 名称 | 2.5.2 椭圆的几何性质(2) 课件(共39张PPT)-人教B版高中数学选择性必修第一册-教案课件习题试卷-高中数学人教版B版选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 22:08:56 | ||
图片预览











文档简介
(共39张PPT)
人教2019B版选择性必修第一册
第二章平面解析几何
2.5.2椭圆的几何性质(2)
1.根据几何条件求出曲线方程,利用曲线的方程研究它的性质.
2.椭圆离心率的求解问题.
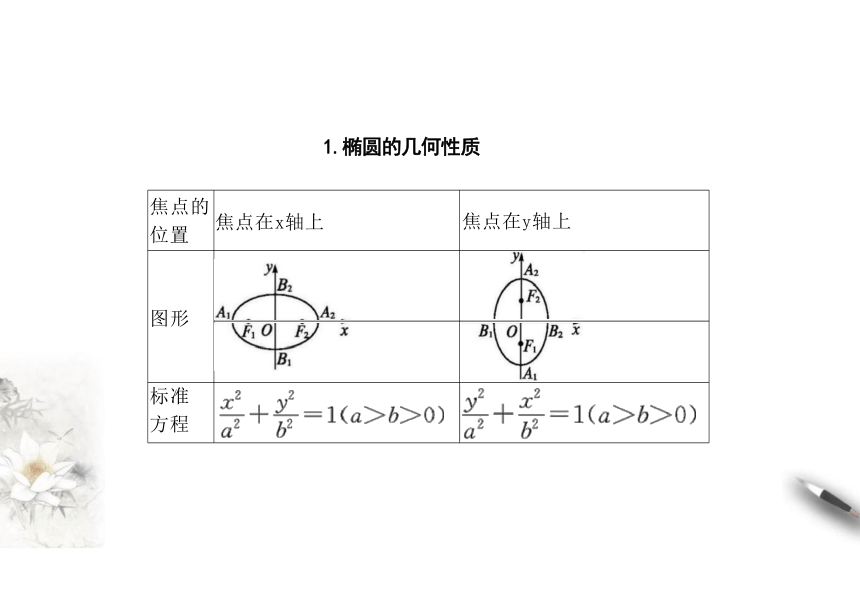
焦点的 位置 焦点在x轴上
焦点在y轴上
图形
标准 方程
1.椭圆的几何性质
焦点的 位置 焦点在x轴上
焦点在y轴上
范围 a≤x≤a且-b≤y≤b
-b≤x≤b且-a≤y≤a
顶点 B (0,-b),B (0,b)
B (-b,0),B (b,0)
轴长 长轴长为2a,短轴长为2b
焦点 F (-c,0),F (c,0)
H ,c)
焦距 2c
对称性 C (0,1),其中 C U 2
离心率 a
2.离心率
C
(1)定义:椭圆的焦距与长轴长的比_a _称为椭圆的 离心率 (0,1)
(2)性质:离心率e的范围是 . 当e越接近于1时,椭圆_ 越 扁;当e越
接近于 0时,椭圆就越接近于圆.
【答案】A
【解析】若△ AF B 的周长为4√3,由椭圆的定义可知4a=4√3,
∴a=√3,
∴c=1,∴b =2,
所以方程为 故选A.
的左右焦点为F ,F 离心率为 过 F 的直线1交C 与 A,B 两
点,若△ AF B的周长为4√3,则C 的方程为()
1. (2014 ·全国高考)已知椭圆(C:
2. (2016 · 全国高考)直线1经过椭圆的一个顶点和一个焦点,若椭圆中心到1的距离为其短轴
长的
A.
即bx+cy-bc=0→椭圆中心到1的距离
,则该椭圆的离心率为( )
【解析】不妨设直线
【答案】B
故选B.
D.
C.
B.
事
【答案】C
【解析】如下图所示,△F PF是底角为30的等腰三角形,则有|FF |=|PF|,∠PFF=∠F PF=30,
所以∠PF A=60,∠F PA=30,
所以
又因为EF|=2c, 所以,2c=3a-2c,所 以
3 . (2012 · 全国高考)设F、F 是 椭 圆 的 左 、 右 焦 点 ,P 为 直 线 上
一点,△F PF是底角为30的等腰三角形,则E 的 离 心 率 为 ( )
A. B. C. D.
类型一 利用几何性质求椭圆的标准方程
例1、 求适合下列条件的椭圆的标准方程:
(1)椭圆过点(3,0),离心率
(2)在x 轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为8;
(3)求经过点M(1,2), 且与椭 有相同离心率的椭圆的标准方程.
[解](1)若焦点在x 轴上,则a=3,
, ∴c=√6,
∴b =a —c =9—6=3.
∴椭圆的方程为
若焦点在y 轴上,则b=3,
∴所求椭圆的方程为
∴椭圆的方程为
解得a =27.
··
垂
(2)设椭圆方程为
如图所示,△A FA 为等腰直角三角形,
OF 为斜边A A 的中线(高),
且|OF|=c,|A A |=2b,
故所求椭圆的方程为
∴c=b=4,∴a =b +c =32,
解得 或b =3.
故所求椭圆方程为
设所求椭圆的方程为
将点M(1,2)代入椭圆方程得
所) 即a =2b
(3)法一:由题意知
·
法 二: 设 所 求 椭 圆 方 程 为 或 将 点M 的
坐 标 代 入 可 得 解 得
即 所 求 椭 圆 的 标 准 方 程 为
故
,
利用椭圆的几何性质求标准方程的思路
1. 利用椭圆的几何性质求椭圆的标准方程时,通常采用待定系数法,其步骤 是:
(1)确定焦点位置;
(2)设出相应椭圆的标准方程(对于焦点位置不确定的椭圆可能有两种标准方 程);
(3)根据已知条件构造关于参数的关系式,利用方程(组)求参数,列方程(组)时
常用的关系式有b =a —c ,
。
2.在椭圆的简单几何性质中,轴长、离心率不能确定椭圆的焦点位置,因此
仅依据这些条件求所要确定的椭圆的标准方程可能有两个.
提醒:与椭圆 有相同离心率的椭圆方程为
焦点在x 轴上) ,焦点在y 轴上).
跟踪训练1. (1)若椭圆的对称轴为坐标轴,长轴长与短轴长的和为18,一个
焦点的坐标是(3,0),则椭圆的标准方程为( )
B [由题意,得
解得
因为椭圆的焦点在x 轴上,
所以椭圆的标准方程为
答案:
[因为椭圆的长轴长是6,
所以点A 不是长轴的端点(是短轴的端点).所以|OF|=c,|AF|=a=3,
顶点,椭圆的长轴长为6, 则椭圆的标准方程是
所以 所以c=2,b =3 —2 =5,
所以椭圆的方程
(2)已知椭圆的对称轴是坐标轴,O 为坐标原点,F 是 一 个焦点,A 是 一 个
类型二 求椭圆的离心率
例2、(1) 已 知F 是椭圆的左焦点,A,B 分别是其在x 轴正半轴和y 轴正半 轴上的顶点,P 是椭圆上的一点,且PF⊥x 轴 ,OP//AB, 怎样求椭圆的离心 率
解:如图,设椭圆的方程 ,P (一c,m).
∵OP//AB,
∴△PFO∽△BOA,
将①代入②,得
即 ,∴
又P(一c,m) 在椭圆上,
①
②
(2). 已知椭 的左焦点为 F (一c,0),A(—a,0),B(O,b)
是两个顶点,如果F 到直线AB 的距离 求椭圆的离心率e.
解:由A(—a,0),B(0,b), 得直线AB的斜率为
故AB 所在的直线方程为
即bx—ay+ab=0.
又F (一c,0),由点到直线的距离公式可得
∴√ 7.(a—c)=√a +b .
∴8e —14e+5=0,∴ 舍去).
综上可知,椭圆的离心率
又b =a —c ,
整理,得8c — 14ac+5a =0,
例3、已 知F ,F 是椭圆的两个焦点,过F 且与椭圆长轴垂直的直线交
椭圆于A,B 两点,若△ABF, 是正三角形,则该椭圆的离心率是
[思路探究] △ ABF 为正三角形→ ∠AF F =30°→ 把 A|F I,|AF I 用 C 表 示 .
解 : 不妨设椭圆的焦点在x 轴上,因为AB⊥F F , 且 △ABF 为正三角形,
所以在Rt△AF F 中,∠AF F =30°, 令|AF |=x, 则 |AF I=2x, 所以 |F F I= √ IAF I -|AF P = √3x=2c, 再由椭圆的定义,可知|AF I+|AF I=2a=3x,
[答案]
所以
求椭圆离心率及范围的两种方法
(1)直接法:若已知a,c 可直接利用 解 . 若已知a,b 或 b,c 可借助于 a =b +c 求 出c 或 a, 再代入公式 求解.
(2)方程法:若a,c 的值不可求,则可根据条件建立a,b,c 的关系式,借助 于 a =b +c , 转化为关于a,c 的齐次方程或不等式,再将方程或不等式两 边同除以a 的最高次幂,得到关于e 的方程或不等式,即可求得e 的值或范 围 .
跟踪训练2. (1)椭 的一个焦点为F, 该椭圆上有一点A,
满足△OAF 是等边三角形(0为坐标原点),则椭圆的离心率是( )
A.√3- 1 B.2-√3 C.2- 1 D.2-√2
(2)椭 的两焦点为 F ,F , 以 F F 为边作正三角形,若椭
圆恰好平分正三角形的另两条边,则椭圆的离心率为
(1)A (2)√3-1
[(1)如图,设F(c,0), 由△OAF 是等边三角形,
因为点A 在椭圆上,所以 ①,
在椭圆中有a =b +c ②, 联立①②,得c =(4-2√3)a ,
即c=(√3-1)a, 则其离心率
得
∵|NF I=c,
∴|NF I=√IF F P —INF I =√4c —c =√3c,
由椭圆的定义可知|NF I+|NF I=2a, ∴3c+c=2a,
(2)法一 如图,∵△DF F 为正三角形,N 为 DF 的 中 点 ,∴F N⊥F N,
法二 注意到焦点三角形NF F 中,∠NF F =30°,∠NF F =60°,
∠F NF =9 0°,则由离心率的三角形式,可得
1.已知椭 有相同的长轴,椭
1(a>b>0) 的短轴长 的短轴长相等,则( )
A.a =15,b =16
C.a =25,b =9
B.a =9,b =25
D.a =25,b =9
或a =9,b =25
【答案】D
[由题意得,椭圆 的焦点在x 轴上,且a =25,b =9.]
2. (2018 ·全国高考)已知椭圆 的一个焦点为(2,0),则C 的 离 心 率 为 ( )
A. B. C. D.
【答案】C
【解析】根据题意,可知c=2, 因 为b =4,
所以a =b +c =8, 即 a=2√2,
所以椭圆C的离心率为 故选C.
【答案】B
【解析】法一:如图,由已知可设|FB|=n,则A|F |=2n,BF|=|AB|=3n,由椭圆的定义有 2a=|BF|+|BF |=4n,:|AF|=2a-|AF |=2n.在△AFB中,由余弦定理推论得
在△AFF 中,由余弦定理得 .2a=4n=2J3,:a=√3,:.b =a -c =3-1=2,所求椭圆方程为 故选B.
3. (2019 ·全国高考)已知椭圆C 的焦点为F(-1,0),F (1,0),过 F 的直线与C 交于 A,B 两点.
若 |AF l=2|F B, |AB|=|BF|,则 C 的方程为
A.
D.
C.
B.
法二:由已知可设F| B=n,则 A|F |=2n,BF|=|AB|=3n,由椭圆的定义有
2a=|BF|+|BF |=4n,:.AF|=2a-|AF|=2n.在△AFF 和△BFF 中,由余弦定理得
∴2a=4n=2√3,:a=√3,∴b =a -c =3-1=2,:
故选B.
得3n +6=11n ,解得
所求椭圆方程为
又∠AF F,∠BF F互补,∴.cos ∠AF F+cos ∠BF F=0,
两式消去cos ∠AF F,cos ∠BF F,
4. (2017 · 全国高考)已知椭圆 的左、右顶点分别为A ,A , 且以线段
A A 为直径的圆与直线bx-ay+2ab=0相切,则C 的离心率为( )
A. B. C. D.
【答案】A
【解析】以线段AA 为直径的圆的圆心为坐标原点(0,0),半径为r=a, 圆的方程为x +y =a ,
直线bx-ay+2ab=0与圆相切,所以圆心到直线的距离等于半径,即
a =3b , 即 a =3(a -c ),即2a =3c ,从 而 则椭圆的离心率
整理可得
故选A.
【答案】
【解析】设A(x,y),B(x ,y ), 则 ①, ②,
∵M是线段AB 的中点, ∴ 2 9
∵直线AB的方程是 ,∴
∵过点M(1,1) 作斜率为 的直线与椭圆C: (a>b>0)
5 . 过 点M(1,1)作 斜 率 的直线与椭圆C: 相交于A,B, 若 M 是线段AB的 中
点,则椭圆C 的离心率为
相交于 A,B 两点,M 是线段AB的中点,∴①②两式相减可得
即 ∴a=√2b:.c=b
事
。
1.根据几何条件求出曲线方程,利用曲线的方程研究它的性质.
2.椭圆离心率的求解问题.
人教2019B版选择性必修第一册
第二章平面解析几何
2.5.2椭圆的几何性质(2)
1.根据几何条件求出曲线方程,利用曲线的方程研究它的性质.
2.椭圆离心率的求解问题.
焦点的 位置 焦点在x轴上
焦点在y轴上
图形
标准 方程
1.椭圆的几何性质
焦点的 位置 焦点在x轴上
焦点在y轴上
范围 a≤x≤a且-b≤y≤b
-b≤x≤b且-a≤y≤a
顶点 B (0,-b),B (0,b)
B (-b,0),B (b,0)
轴长 长轴长为2a,短轴长为2b
焦点 F (-c,0),F (c,0)
H ,c)
焦距 2c
对称性 C (0,1),其中 C U 2
离心率 a
2.离心率
C
(1)定义:椭圆的焦距与长轴长的比_a _称为椭圆的 离心率 (0,1)
(2)性质:离心率e的范围是 . 当e越接近于1时,椭圆_ 越 扁;当e越
接近于 0时,椭圆就越接近于圆.
【答案】A
【解析】若△ AF B 的周长为4√3,由椭圆的定义可知4a=4√3,
∴a=√3,
∴c=1,∴b =2,
所以方程为 故选A.
的左右焦点为F ,F 离心率为 过 F 的直线1交C 与 A,B 两
点,若△ AF B的周长为4√3,则C 的方程为()
1. (2014 ·全国高考)已知椭圆(C:
2. (2016 · 全国高考)直线1经过椭圆的一个顶点和一个焦点,若椭圆中心到1的距离为其短轴
长的
A.
即bx+cy-bc=0→椭圆中心到1的距离
,则该椭圆的离心率为( )
【解析】不妨设直线
【答案】B
故选B.
D.
C.
B.
事
【答案】C
【解析】如下图所示,△F PF是底角为30的等腰三角形,则有|FF |=|PF|,∠PFF=∠F PF=30,
所以∠PF A=60,∠F PA=30,
所以
又因为EF|=2c, 所以,2c=3a-2c,所 以
3 . (2012 · 全国高考)设F、F 是 椭 圆 的 左 、 右 焦 点 ,P 为 直 线 上
一点,△F PF是底角为30的等腰三角形,则E 的 离 心 率 为 ( )
A. B. C. D.
类型一 利用几何性质求椭圆的标准方程
例1、 求适合下列条件的椭圆的标准方程:
(1)椭圆过点(3,0),离心率
(2)在x 轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为8;
(3)求经过点M(1,2), 且与椭 有相同离心率的椭圆的标准方程.
[解](1)若焦点在x 轴上,则a=3,
, ∴c=√6,
∴b =a —c =9—6=3.
∴椭圆的方程为
若焦点在y 轴上,则b=3,
∴所求椭圆的方程为
∴椭圆的方程为
解得a =27.
··
垂
(2)设椭圆方程为
如图所示,△A FA 为等腰直角三角形,
OF 为斜边A A 的中线(高),
且|OF|=c,|A A |=2b,
故所求椭圆的方程为
∴c=b=4,∴a =b +c =32,
解得 或b =3.
故所求椭圆方程为
设所求椭圆的方程为
将点M(1,2)代入椭圆方程得
所) 即a =2b
(3)法一:由题意知
·
法 二: 设 所 求 椭 圆 方 程 为 或 将 点M 的
坐 标 代 入 可 得 解 得
即 所 求 椭 圆 的 标 准 方 程 为
故
,
利用椭圆的几何性质求标准方程的思路
1. 利用椭圆的几何性质求椭圆的标准方程时,通常采用待定系数法,其步骤 是:
(1)确定焦点位置;
(2)设出相应椭圆的标准方程(对于焦点位置不确定的椭圆可能有两种标准方 程);
(3)根据已知条件构造关于参数的关系式,利用方程(组)求参数,列方程(组)时
常用的关系式有b =a —c ,
。
2.在椭圆的简单几何性质中,轴长、离心率不能确定椭圆的焦点位置,因此
仅依据这些条件求所要确定的椭圆的标准方程可能有两个.
提醒:与椭圆 有相同离心率的椭圆方程为
焦点在x 轴上) ,焦点在y 轴上).
跟踪训练1. (1)若椭圆的对称轴为坐标轴,长轴长与短轴长的和为18,一个
焦点的坐标是(3,0),则椭圆的标准方程为( )
B [由题意,得
解得
因为椭圆的焦点在x 轴上,
所以椭圆的标准方程为
答案:
[因为椭圆的长轴长是6,
所以点A 不是长轴的端点(是短轴的端点).所以|OF|=c,|AF|=a=3,
顶点,椭圆的长轴长为6, 则椭圆的标准方程是
所以 所以c=2,b =3 —2 =5,
所以椭圆的方程
(2)已知椭圆的对称轴是坐标轴,O 为坐标原点,F 是 一 个焦点,A 是 一 个
类型二 求椭圆的离心率
例2、(1) 已 知F 是椭圆的左焦点,A,B 分别是其在x 轴正半轴和y 轴正半 轴上的顶点,P 是椭圆上的一点,且PF⊥x 轴 ,OP//AB, 怎样求椭圆的离心 率
解:如图,设椭圆的方程 ,P (一c,m).
∵OP//AB,
∴△PFO∽△BOA,
将①代入②,得
即 ,∴
又P(一c,m) 在椭圆上,
①
②
(2). 已知椭 的左焦点为 F (一c,0),A(—a,0),B(O,b)
是两个顶点,如果F 到直线AB 的距离 求椭圆的离心率e.
解:由A(—a,0),B(0,b), 得直线AB的斜率为
故AB 所在的直线方程为
即bx—ay+ab=0.
又F (一c,0),由点到直线的距离公式可得
∴√ 7.(a—c)=√a +b .
∴8e —14e+5=0,∴ 舍去).
综上可知,椭圆的离心率
又b =a —c ,
整理,得8c — 14ac+5a =0,
例3、已 知F ,F 是椭圆的两个焦点,过F 且与椭圆长轴垂直的直线交
椭圆于A,B 两点,若△ABF, 是正三角形,则该椭圆的离心率是
[思路探究] △ ABF 为正三角形→ ∠AF F =30°→ 把 A|F I,|AF I 用 C 表 示 .
解 : 不妨设椭圆的焦点在x 轴上,因为AB⊥F F , 且 △ABF 为正三角形,
所以在Rt△AF F 中,∠AF F =30°, 令|AF |=x, 则 |AF I=2x, 所以 |F F I= √ IAF I -|AF P = √3x=2c, 再由椭圆的定义,可知|AF I+|AF I=2a=3x,
[答案]
所以
求椭圆离心率及范围的两种方法
(1)直接法:若已知a,c 可直接利用 解 . 若已知a,b 或 b,c 可借助于 a =b +c 求 出c 或 a, 再代入公式 求解.
(2)方程法:若a,c 的值不可求,则可根据条件建立a,b,c 的关系式,借助 于 a =b +c , 转化为关于a,c 的齐次方程或不等式,再将方程或不等式两 边同除以a 的最高次幂,得到关于e 的方程或不等式,即可求得e 的值或范 围 .
跟踪训练2. (1)椭 的一个焦点为F, 该椭圆上有一点A,
满足△OAF 是等边三角形(0为坐标原点),则椭圆的离心率是( )
A.√3- 1 B.2-√3 C.2- 1 D.2-√2
(2)椭 的两焦点为 F ,F , 以 F F 为边作正三角形,若椭
圆恰好平分正三角形的另两条边,则椭圆的离心率为
(1)A (2)√3-1
[(1)如图,设F(c,0), 由△OAF 是等边三角形,
因为点A 在椭圆上,所以 ①,
在椭圆中有a =b +c ②, 联立①②,得c =(4-2√3)a ,
即c=(√3-1)a, 则其离心率
得
∵|NF I=c,
∴|NF I=√IF F P —INF I =√4c —c =√3c,
由椭圆的定义可知|NF I+|NF I=2a, ∴3c+c=2a,
(2)法一 如图,∵△DF F 为正三角形,N 为 DF 的 中 点 ,∴F N⊥F N,
法二 注意到焦点三角形NF F 中,∠NF F =30°,∠NF F =60°,
∠F NF =9 0°,则由离心率的三角形式,可得
1.已知椭 有相同的长轴,椭
1(a>b>0) 的短轴长 的短轴长相等,则( )
A.a =15,b =16
C.a =25,b =9
B.a =9,b =25
D.a =25,b =9
或a =9,b =25
【答案】D
[由题意得,椭圆 的焦点在x 轴上,且a =25,b =9.]
2. (2018 ·全国高考)已知椭圆 的一个焦点为(2,0),则C 的 离 心 率 为 ( )
A. B. C. D.
【答案】C
【解析】根据题意,可知c=2, 因 为b =4,
所以a =b +c =8, 即 a=2√2,
所以椭圆C的离心率为 故选C.
【答案】B
【解析】法一:如图,由已知可设|FB|=n,则A|F |=2n,BF|=|AB|=3n,由椭圆的定义有 2a=|BF|+|BF |=4n,:|AF|=2a-|AF |=2n.在△AFB中,由余弦定理推论得
在△AFF 中,由余弦定理得 .2a=4n=2J3,:a=√3,:.b =a -c =3-1=2,所求椭圆方程为 故选B.
3. (2019 ·全国高考)已知椭圆C 的焦点为F(-1,0),F (1,0),过 F 的直线与C 交于 A,B 两点.
若 |AF l=2|F B, |AB|=|BF|,则 C 的方程为
A.
D.
C.
B.
法二:由已知可设F| B=n,则 A|F |=2n,BF|=|AB|=3n,由椭圆的定义有
2a=|BF|+|BF |=4n,:.AF|=2a-|AF|=2n.在△AFF 和△BFF 中,由余弦定理得
∴2a=4n=2√3,:a=√3,∴b =a -c =3-1=2,:
故选B.
得3n +6=11n ,解得
所求椭圆方程为
又∠AF F,∠BF F互补,∴.cos ∠AF F+cos ∠BF F=0,
两式消去cos ∠AF F,cos ∠BF F,
4. (2017 · 全国高考)已知椭圆 的左、右顶点分别为A ,A , 且以线段
A A 为直径的圆与直线bx-ay+2ab=0相切,则C 的离心率为( )
A. B. C. D.
【答案】A
【解析】以线段AA 为直径的圆的圆心为坐标原点(0,0),半径为r=a, 圆的方程为x +y =a ,
直线bx-ay+2ab=0与圆相切,所以圆心到直线的距离等于半径,即
a =3b , 即 a =3(a -c ),即2a =3c ,从 而 则椭圆的离心率
整理可得
故选A.
【答案】
【解析】设A(x,y),B(x ,y ), 则 ①, ②,
∵M是线段AB 的中点, ∴ 2 9
∵直线AB的方程是 ,∴
∵过点M(1,1) 作斜率为 的直线与椭圆C: (a>b>0)
5 . 过 点M(1,1)作 斜 率 的直线与椭圆C: 相交于A,B, 若 M 是线段AB的 中
点,则椭圆C 的离心率为
相交于 A,B 两点,M 是线段AB的中点,∴①②两式相减可得
即 ∴a=√2b:.c=b
事
。
1.根据几何条件求出曲线方程,利用曲线的方程研究它的性质.
2.椭圆离心率的求解问题.
