2.6.1 双曲线的标准方程 课件(共36张PPT)-人教B版高中数学选择性必修第一册-教案课件习题试卷-高中数学人教版B版选择性必修第一册
文档属性
| 名称 | 2.6.1 双曲线的标准方程 课件(共36张PPT)-人教B版高中数学选择性必修第一册-教案课件习题试卷-高中数学人教版B版选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 00:00:00 | ||
图片预览









文档简介
(共36张PPT)
人教2019B版选择性必修第一册
第二章平面解析几何
2.6.1双曲线的标准方程
1.结合实际情景熟悉双曲线的定义、几何图形和标准方程的推导过程.(逻辑推
理、数学抽象)
2.掌握双曲线的标准方程及其求法.(数学运算)
3.会利用双曲线的定义和标准方程解决简单实际问题.(数学运算) 4.与椭圆的标准方程进行比较,并加以区分. (逻辑推理)
如图所示,某中心O 接到其正西、正东、正北方向三个观测
点A,B,C 的报告:A,C 两个观测点同时听到一声巨响,B 观测 点听到的时间比A 观测点晚4s, 已知各观测点到该中心的距离都是 1020m, 假定当时声音传播的速度为340m/s, 且A,B,C,0 均在同一 平面内.你能确定该巨响发生的点的位置吗
|PBI-|PA|=4×360=1360
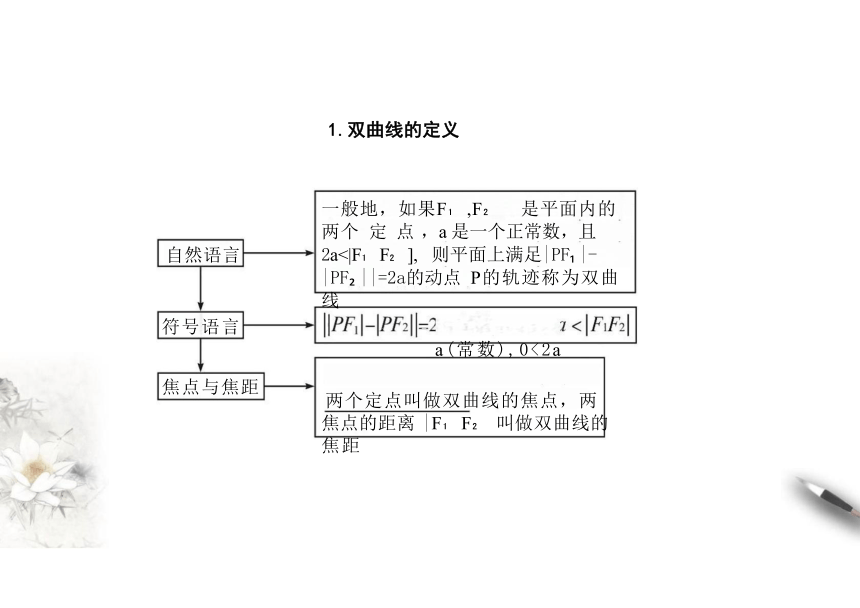
1.双曲线的定义
一般地,如果F ,F 是平面内的两个 定 点 ,a 是一个正常数,且2a<|F F ], 则平面上满足|PF |-|PF ||=2a的动点 P的轨迹称为双曲线
a(常数),0<2a
两个定点叫做双曲线的焦点,两 焦点的距离 |F F 叫做双曲线的 焦距
自然语言
符号语言
焦点与焦距
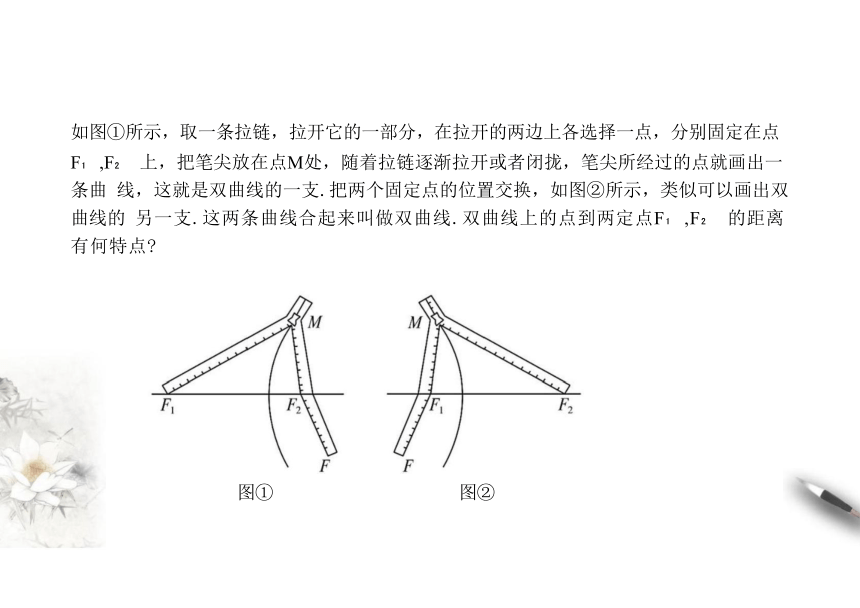
你能利用拉链等日常生活中的物品作出双曲线吗
如图①所示,取一条拉链,拉开它的一部分,在拉开的两边上各选择一点,分别固定在点
F ,F 上,把笔尖放在点M处,随着拉链逐渐拉开或者闭拢,笔尖所经过的点就画出一条曲 线,这就是双曲线的一支.把两个固定点的位置交换,如图②所示,类似可以画出双曲线的 另一支.这两条曲线合起来叫做双曲线.双曲线上的点到两定点F ,F 的距离有何特点
图① 图②
怎样从数学上证明满足双曲线定义的点一定是存在的 这样的点有多少
个 你能想到什么办法来解决这两个问题
从椭圆的情形一样,下面我们用坐标法来探讨尝试与发现中的问题,
并求出双曲线的标准方程。
以F ,F 所在直线为x 轴,线段F F 的垂直平分线为y轴,建立平面直角坐标系x0y, 此时双曲线的焦点分别为F (-c,0),F (c,0)
设P(x,y) 是双曲线上一点,则
因 IPFIP=J-+0 +;IPpI=√x-o +v
所以 √(x+c) +y - √ (x-c) +y =±2a ①
因为c>a>0, 所以c -a >0
设c -a =b
且b>0, 则④可化为
且②与①右边同时取正号或负号,①+②整理得
②
④
设双曲线的焦点为F 和F , 焦距为2c, 而且双曲线上的动点P满足
||PF I-|PF I|=2a, 其中c>a>0, 以F ,F 所在直线为y轴,线段F F 的垂直平分 线为x轴,建立平面直角坐标系,如图所示,此时;
(1)双曲线焦点的坐标分别是什么
(2)能否通 (a>0,b>0), 来得到此双曲线方程形式
焦点位置 焦点在x轴上
焦点在y轴上
图形
标准方程
焦点
a,b,c的关系
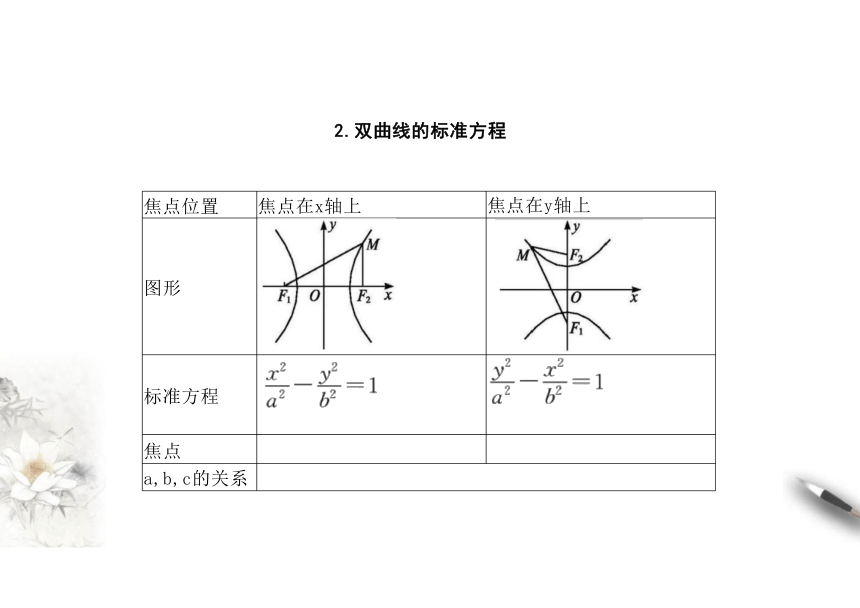
2.双曲线的标准方程
椭圆
双曲线
定义 MF I+|MF I=2a (2a>|F F I)
|MF I-IMF II=2a
(0<2a<|F F I)
a,b,c的关系 b =a -c
b =c -a
标 准 方 程 焦点在 x轴上
焦点在 y轴上
双曲线与椭圆的比较
1.在双曲线的定义中,若去掉条件0<2a<|F F I, 则点的轨迹是怎样的
提 示:①当2a 等于|F F I 时,动点的轨迹是以F ,F 为端点的两条方向 相反的射线(包括端点).
②当 2a大于 |F F I时,动点的轨迹不存在.
③当2a等于零时,动点轨迹为线段F F 的垂直平分线.
2.判断
(1)平面内到两定点的距离的差等于常数(小于两定点间距离)的点的轨迹是双曲线. ( )
(2)平面内到点F (0,4),F (0,-4) 的距离之差等于5的点的轨迹是双曲线. ( )
(3)平面内到点F (0,4),F (0,-4) 的距离之差的绝对值等于8的点的轨迹是双曲线. ( )
答案:(1)×(2)×(3)×
当焦点在x 轴上时,设双曲线方程为
将点(1,1)代入方程中,得
此时双曲线的标准方程为 .同理求得焦点在y 轴上时,双曲线
的标准方程为
答案:D
3.过点(1,1), 的双曲线的标准方程是( )
解析:· ∴b =2a .
分析(1)设双曲线方程 ,代入点的坐标,解方程
即可得到.
(2)可设双曲线方程为mx -ny =1,代入点的坐标,得到方程组,解方程组即可得到.
例1求适合下列条件的双曲线的标准方程.
(1)焦点在x 轴上,a=2√5,经过点A(-5,2);
(2)经过两点A(-7,-6√2),B(2√7,3).
解:(1)设双曲线方程
则a=2√5, 解得b =16,
则双曲线的标准方程为
(2)设双曲线方程为mx -ny =1,
则有 解
则双曲线的标准方程为
求双曲线的标准方程与求椭圆的标准方程的方法相似,可以先根据其焦点
位置设出标准方程,然后用待定系数法求出a,b的值.若焦点位置不确定,可按焦 点在x轴和y轴上两种情况讨论求解,此方法思路清晰,但过程复杂.若双曲线过两 定点,可设其方程为mx +ny =1(mn<0), 通过解方程组即可确定m,n,避免了讨论, 从而简化求解过程.
跟踪训练1根据下列条件,求双曲线的标准方程.
(1)焦点在x 轴上,经过点P(4,-2) 和点Q(2√6,2√2);
(2)过点 且焦点在坐标轴上.
解:(1)因为焦点在x 轴上,
可设双曲线方程为
将点(4,-2)和(2 √6,2
解得a =8,b =4,
所以双曲线的标准方程为
(2)设双曲线的方程为Ax +By =1,AB<0.
因为点P,Q 在双曲线上,
则 解
故双曲线的标准方程为
例2.已知F (-2,0),F (2,0), 动点P满足|PF I-|PF I=2, 求动点P的轨迹方程。
解:因 所以根据双曲线的定义可知,P 一定在a=1,c=2且 焦点在x轴上的双曲线上,这就是说,点P的坐标(x,y)一定满足,
另一方面,由|PF I-|PF I=2>0 可知|PF I>|PF |, 因此P的横坐
标要大于零,从而可知P的轨迹方程为
例3“神舟”九号飞船返回舱顺利到达地球后,为了及时将航天员安全救出,地面指挥中
心在返回舱预计到达区域安排了三个救援中心(记A,B,C),A在B的正东方向,相距6千米,C 在B的北偏西30°方向,相距4千米,P 为航天员着陆点.某一时刻,A接收到P的求救信号,由 于B,C两地比A距P 远,在此4秒后,B,C两个救援中心才同时接收到这一信号.已知该信号 的传播速度为1千米/秒,求在A处发现P的方位角.
所以双曲线方程为
BC 的垂直平分线方程为x-√3y+7=0. 联立两方程解得x=8(舍负),y=5√3, 所以P(8,5 √3),
kpA=tan∠PAx=√3,所以∠PAx=60°,
所以P 点 在A 点的北偏东30°方向.
以线段AB的中点为坐标原点,AB的垂直平分线所在直线为y轴,正东 方向为x轴正方向建立平面直角坐标系,如图所示.
则A(3,0),B(-3,0),C(-5,2√3).
解:因为|PC|=|PB|, 所以P 在线段BC 的垂直平分线上. 又因为|PBI-|PA|=4<6=|AB|,
所以P 在以A,B为焦点的双曲线的右支上.
1.利用双曲线解决实际问题的基本步骤如下:
(1)建立适当的坐标系;
(2)求出双曲线的标准方程;
(3)根据双曲线的方程及定义解决实际应用问题. 2.注意事项:
(1)解答与双曲线有关的应用问题时,除要准确把握题意,了解一些 实际问题的相关概念,同时还要注意双曲线的定义及性质的灵活应 用 .
(2)实际应用问题要注意其实际意义以及在该意义下隐藏着的变量 范围.
跟踪训练2 一块面积为12公顷的三角形形状的农场.如图所示△PEF,已知
,tan∠PFE=-2,试建立适当直角坐标系,求出分别以E,F为左、右焦 点且过点P的双曲线方程.
设以E,F 为焦点且过点P 的双曲线方程为 焦点为E(-c,0),F(c,0).
由
设∠PFx=a, 则tan a=tan(π-∠EFP)=2,
得直线PE 和直线PF 的方程分别为 和 y=2(x-c).
联立两方程,解得 即P 点坐标为
解:以E,F所在直线为x轴,EF 的垂直平分线为y轴建立直角坐标系,如图.
∵在△EFP 中,|EF|=2c,EF 上的高为点P 的纵坐标,
∴c=3, 即P 点坐标为(5,4).
由两点间的距离公式
∴a=√5.又b =c -a =4,
故所求双曲线的方程为
错解:将双曲线方程化为标准方程为
由题意知焦点在y 轴上,所以
所以
所以
错因分析上述解法有两处错误:一是a ,b 确定错误,应该是a =-
是a,b,c的关系式用错了,在双曲线中应为c =a +b .
典例 已知双曲线8kx -ky =8的一个焦点为(0,3),求k的值.
正解:将双曲线方程化为
因为一个焦点是(0,3), 所以焦点在y 轴上,所以c=3, 所以 所以k=-1.
1.已知两定点F (-5,0),F (5,0), 动点P 满足|PF I-|PF I=2a, 则当a=3 和5时,P点的轨迹为( )
A.双曲线和一条直线
B.双曲线和一条射线
C.双曲线的一支和一条直线
D.双曲线的一支和一条射线
解析:当a=3 时,根据双曲线的定义及|PF I>|PF I 可推断出其轨迹是双曲线
的一支.当a=5 时,方程y =0, 可知其轨迹与x轴重合,舍去在x轴负半轴上的
一段,又因为|PF I-IPF I=2a, 说明|PF I>|PF I, 所以应该是起点为(5,0),与x
轴重合向x轴正方向延伸的射线.
支相交,且所得弦长|AB|=m, 则△ABF 的周长为( )
A.4a B.4a-m
C.4a+2m D.4a-2m
解析:不妨设|AF I>|AF I,由双曲线的定义,知|AF I-AF I=2a,|BF I-IBF I=2a,
所以|AF I+|BF I=(|AF I+|BF I)+4a=m+4a, 于是△ABF 的周长 l=|AF I+|BF I+|AB|=4a+2m. 故选C.
答案:C
(a>0 h>0).F .F,为其两个焦点,若过焦点F 的直线与双曲线的同一
2.已知双曲线
解 析:∵方 , ∴(m-2)(m+1)<0,
解得-1答案:D
3. 已知方 表示双曲线,则m 的取值范围是( )
A.(-1,+0)
C. (-00,-1)U(2,+0)
B.(2,+0)
D. (-1,2)
4.经过点P(-3,2√7)和Q(-6√2,-7),且焦点在y轴上的双曲线的标准方 程是
解析:设双曲线的方程为mx +ny =1(mn<0),
则 解得
故双曲线的标准方程为
答案
5.求适合下列条件的双曲线的标准方程.
(1)两个焦点的坐标分别是(-5,0),(5,0),双曲线上的点与两焦点的距离之差的绝对值等于8;
(2)以椭 长轴的端点为焦点,且经过点(3, √ 10);
(3)a=b, 经过点(3,-1).
解:(1)由双曲线的定义知,2a=8,所以a=4, 又知焦点在x轴上,且c=5,
所以b =c -a =25-16=9,
所以双曲线的标准方程为
(2)由题意得,双曲线的焦点在x 轴上,且c=2√2.
设双曲线的标准方程为
则有
解得a =3,b =5.
故所求双曲线的标准方程为
(3)当焦点在x 轴上时,可设双曲线方程为x -y =a , 将点(3,-1)代入, 得3 -(-1) =a ,
所以a =b =8. 因此,所求的双曲线的标准方程
当焦点在y 轴上时,可设双曲线方程为y -x =a , 将点(3,-1)代入,得(- 1) -3 =a ,a =-8,不可能,所以焦点不可能在y 轴上.
综上,所求双曲线的标准方程为
焦点
定义
焦距
标准方程
实际应用
双曲线
人教2019B版选择性必修第一册
第二章平面解析几何
2.6.1双曲线的标准方程
1.结合实际情景熟悉双曲线的定义、几何图形和标准方程的推导过程.(逻辑推
理、数学抽象)
2.掌握双曲线的标准方程及其求法.(数学运算)
3.会利用双曲线的定义和标准方程解决简单实际问题.(数学运算) 4.与椭圆的标准方程进行比较,并加以区分. (逻辑推理)
如图所示,某中心O 接到其正西、正东、正北方向三个观测
点A,B,C 的报告:A,C 两个观测点同时听到一声巨响,B 观测 点听到的时间比A 观测点晚4s, 已知各观测点到该中心的距离都是 1020m, 假定当时声音传播的速度为340m/s, 且A,B,C,0 均在同一 平面内.你能确定该巨响发生的点的位置吗
|PBI-|PA|=4×360=1360
1.双曲线的定义
一般地,如果F ,F 是平面内的两个 定 点 ,a 是一个正常数,且2a<|F F ], 则平面上满足|PF |-|PF ||=2a的动点 P的轨迹称为双曲线
a(常数),0<2a
两个定点叫做双曲线的焦点,两 焦点的距离 |F F 叫做双曲线的 焦距
自然语言
符号语言
焦点与焦距
你能利用拉链等日常生活中的物品作出双曲线吗
如图①所示,取一条拉链,拉开它的一部分,在拉开的两边上各选择一点,分别固定在点
F ,F 上,把笔尖放在点M处,随着拉链逐渐拉开或者闭拢,笔尖所经过的点就画出一条曲 线,这就是双曲线的一支.把两个固定点的位置交换,如图②所示,类似可以画出双曲线的 另一支.这两条曲线合起来叫做双曲线.双曲线上的点到两定点F ,F 的距离有何特点
图① 图②
怎样从数学上证明满足双曲线定义的点一定是存在的 这样的点有多少
个 你能想到什么办法来解决这两个问题
从椭圆的情形一样,下面我们用坐标法来探讨尝试与发现中的问题,
并求出双曲线的标准方程。
以F ,F 所在直线为x 轴,线段F F 的垂直平分线为y轴,建立平面直角坐标系x0y, 此时双曲线的焦点分别为F (-c,0),F (c,0)
设P(x,y) 是双曲线上一点,则
因 IPFIP=J-+0 +;IPpI=√x-o +v
所以 √(x+c) +y - √ (x-c) +y =±2a ①
因为c>a>0, 所以c -a >0
设c -a =b
且b>0, 则④可化为
且②与①右边同时取正号或负号,①+②整理得
②
④
设双曲线的焦点为F 和F , 焦距为2c, 而且双曲线上的动点P满足
||PF I-|PF I|=2a, 其中c>a>0, 以F ,F 所在直线为y轴,线段F F 的垂直平分 线为x轴,建立平面直角坐标系,如图所示,此时;
(1)双曲线焦点的坐标分别是什么
(2)能否通 (a>0,b>0), 来得到此双曲线方程形式
焦点位置 焦点在x轴上
焦点在y轴上
图形
标准方程
焦点
a,b,c的关系
2.双曲线的标准方程
椭圆
双曲线
定义 MF I+|MF I=2a (2a>|F F I)
|MF I-IMF II=2a
(0<2a<|F F I)
a,b,c的关系 b =a -c
b =c -a
标 准 方 程 焦点在 x轴上
焦点在 y轴上
双曲线与椭圆的比较
1.在双曲线的定义中,若去掉条件0<2a<|F F I, 则点的轨迹是怎样的
提 示:①当2a 等于|F F I 时,动点的轨迹是以F ,F 为端点的两条方向 相反的射线(包括端点).
②当 2a大于 |F F I时,动点的轨迹不存在.
③当2a等于零时,动点轨迹为线段F F 的垂直平分线.
2.判断
(1)平面内到两定点的距离的差等于常数(小于两定点间距离)的点的轨迹是双曲线. ( )
(2)平面内到点F (0,4),F (0,-4) 的距离之差等于5的点的轨迹是双曲线. ( )
(3)平面内到点F (0,4),F (0,-4) 的距离之差的绝对值等于8的点的轨迹是双曲线. ( )
答案:(1)×(2)×(3)×
当焦点在x 轴上时,设双曲线方程为
将点(1,1)代入方程中,得
此时双曲线的标准方程为 .同理求得焦点在y 轴上时,双曲线
的标准方程为
答案:D
3.过点(1,1), 的双曲线的标准方程是( )
解析:· ∴b =2a .
分析(1)设双曲线方程 ,代入点的坐标,解方程
即可得到.
(2)可设双曲线方程为mx -ny =1,代入点的坐标,得到方程组,解方程组即可得到.
例1求适合下列条件的双曲线的标准方程.
(1)焦点在x 轴上,a=2√5,经过点A(-5,2);
(2)经过两点A(-7,-6√2),B(2√7,3).
解:(1)设双曲线方程
则a=2√5, 解得b =16,
则双曲线的标准方程为
(2)设双曲线方程为mx -ny =1,
则有 解
则双曲线的标准方程为
求双曲线的标准方程与求椭圆的标准方程的方法相似,可以先根据其焦点
位置设出标准方程,然后用待定系数法求出a,b的值.若焦点位置不确定,可按焦 点在x轴和y轴上两种情况讨论求解,此方法思路清晰,但过程复杂.若双曲线过两 定点,可设其方程为mx +ny =1(mn<0), 通过解方程组即可确定m,n,避免了讨论, 从而简化求解过程.
跟踪训练1根据下列条件,求双曲线的标准方程.
(1)焦点在x 轴上,经过点P(4,-2) 和点Q(2√6,2√2);
(2)过点 且焦点在坐标轴上.
解:(1)因为焦点在x 轴上,
可设双曲线方程为
将点(4,-2)和(2 √6,2
解得a =8,b =4,
所以双曲线的标准方程为
(2)设双曲线的方程为Ax +By =1,AB<0.
因为点P,Q 在双曲线上,
则 解
故双曲线的标准方程为
例2.已知F (-2,0),F (2,0), 动点P满足|PF I-|PF I=2, 求动点P的轨迹方程。
解:因 所以根据双曲线的定义可知,P 一定在a=1,c=2且 焦点在x轴上的双曲线上,这就是说,点P的坐标(x,y)一定满足,
另一方面,由|PF I-|PF I=2>0 可知|PF I>|PF |, 因此P的横坐
标要大于零,从而可知P的轨迹方程为
例3“神舟”九号飞船返回舱顺利到达地球后,为了及时将航天员安全救出,地面指挥中
心在返回舱预计到达区域安排了三个救援中心(记A,B,C),A在B的正东方向,相距6千米,C 在B的北偏西30°方向,相距4千米,P 为航天员着陆点.某一时刻,A接收到P的求救信号,由 于B,C两地比A距P 远,在此4秒后,B,C两个救援中心才同时接收到这一信号.已知该信号 的传播速度为1千米/秒,求在A处发现P的方位角.
所以双曲线方程为
BC 的垂直平分线方程为x-√3y+7=0. 联立两方程解得x=8(舍负),y=5√3, 所以P(8,5 √3),
kpA=tan∠PAx=√3,所以∠PAx=60°,
所以P 点 在A 点的北偏东30°方向.
以线段AB的中点为坐标原点,AB的垂直平分线所在直线为y轴,正东 方向为x轴正方向建立平面直角坐标系,如图所示.
则A(3,0),B(-3,0),C(-5,2√3).
解:因为|PC|=|PB|, 所以P 在线段BC 的垂直平分线上. 又因为|PBI-|PA|=4<6=|AB|,
所以P 在以A,B为焦点的双曲线的右支上.
1.利用双曲线解决实际问题的基本步骤如下:
(1)建立适当的坐标系;
(2)求出双曲线的标准方程;
(3)根据双曲线的方程及定义解决实际应用问题. 2.注意事项:
(1)解答与双曲线有关的应用问题时,除要准确把握题意,了解一些 实际问题的相关概念,同时还要注意双曲线的定义及性质的灵活应 用 .
(2)实际应用问题要注意其实际意义以及在该意义下隐藏着的变量 范围.
跟踪训练2 一块面积为12公顷的三角形形状的农场.如图所示△PEF,已知
,tan∠PFE=-2,试建立适当直角坐标系,求出分别以E,F为左、右焦 点且过点P的双曲线方程.
设以E,F 为焦点且过点P 的双曲线方程为 焦点为E(-c,0),F(c,0).
由
设∠PFx=a, 则tan a=tan(π-∠EFP)=2,
得直线PE 和直线PF 的方程分别为 和 y=2(x-c).
联立两方程,解得 即P 点坐标为
解:以E,F所在直线为x轴,EF 的垂直平分线为y轴建立直角坐标系,如图.
∵在△EFP 中,|EF|=2c,EF 上的高为点P 的纵坐标,
∴c=3, 即P 点坐标为(5,4).
由两点间的距离公式
∴a=√5.又b =c -a =4,
故所求双曲线的方程为
错解:将双曲线方程化为标准方程为
由题意知焦点在y 轴上,所以
所以
所以
错因分析上述解法有两处错误:一是a ,b 确定错误,应该是a =-
是a,b,c的关系式用错了,在双曲线中应为c =a +b .
典例 已知双曲线8kx -ky =8的一个焦点为(0,3),求k的值.
正解:将双曲线方程化为
因为一个焦点是(0,3), 所以焦点在y 轴上,所以c=3, 所以 所以k=-1.
1.已知两定点F (-5,0),F (5,0), 动点P 满足|PF I-|PF I=2a, 则当a=3 和5时,P点的轨迹为( )
A.双曲线和一条直线
B.双曲线和一条射线
C.双曲线的一支和一条直线
D.双曲线的一支和一条射线
解析:当a=3 时,根据双曲线的定义及|PF I>|PF I 可推断出其轨迹是双曲线
的一支.当a=5 时,方程y =0, 可知其轨迹与x轴重合,舍去在x轴负半轴上的
一段,又因为|PF I-IPF I=2a, 说明|PF I>|PF I, 所以应该是起点为(5,0),与x
轴重合向x轴正方向延伸的射线.
支相交,且所得弦长|AB|=m, 则△ABF 的周长为( )
A.4a B.4a-m
C.4a+2m D.4a-2m
解析:不妨设|AF I>|AF I,由双曲线的定义,知|AF I-AF I=2a,|BF I-IBF I=2a,
所以|AF I+|BF I=(|AF I+|BF I)+4a=m+4a, 于是△ABF 的周长 l=|AF I+|BF I+|AB|=4a+2m. 故选C.
答案:C
(a>0 h>0).F .F,为其两个焦点,若过焦点F 的直线与双曲线的同一
2.已知双曲线
解 析:∵方 , ∴(m-2)(m+1)<0,
解得-1
3. 已知方 表示双曲线,则m 的取值范围是( )
A.(-1,+0)
C. (-00,-1)U(2,+0)
B.(2,+0)
D. (-1,2)
4.经过点P(-3,2√7)和Q(-6√2,-7),且焦点在y轴上的双曲线的标准方 程是
解析:设双曲线的方程为mx +ny =1(mn<0),
则 解得
故双曲线的标准方程为
答案
5.求适合下列条件的双曲线的标准方程.
(1)两个焦点的坐标分别是(-5,0),(5,0),双曲线上的点与两焦点的距离之差的绝对值等于8;
(2)以椭 长轴的端点为焦点,且经过点(3, √ 10);
(3)a=b, 经过点(3,-1).
解:(1)由双曲线的定义知,2a=8,所以a=4, 又知焦点在x轴上,且c=5,
所以b =c -a =25-16=9,
所以双曲线的标准方程为
(2)由题意得,双曲线的焦点在x 轴上,且c=2√2.
设双曲线的标准方程为
则有
解得a =3,b =5.
故所求双曲线的标准方程为
(3)当焦点在x 轴上时,可设双曲线方程为x -y =a , 将点(3,-1)代入, 得3 -(-1) =a ,
所以a =b =8. 因此,所求的双曲线的标准方程
当焦点在y 轴上时,可设双曲线方程为y -x =a , 将点(3,-1)代入,得(- 1) -3 =a ,a =-8,不可能,所以焦点不可能在y 轴上.
综上,所求双曲线的标准方程为
焦点
定义
焦距
标准方程
实际应用
双曲线
