2.6.2 双曲线的几何性质(1) 课件(共31张PPT)-人教B版高中数学选择性必修第一册-教案课件习题试卷-高中数学人教版B版选择性必修第一册
文档属性
| 名称 | 2.6.2 双曲线的几何性质(1) 课件(共31张PPT)-人教B版高中数学选择性必修第一册-教案课件习题试卷-高中数学人教版B版选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 22:11:41 | ||
图片预览










文档简介
(共31张PPT)
人教2019B版选择性必修第一册
第二章平面解析几何
2.6.2双曲线的几何性质(1)
1.掌握双曲线的简单几何性质. (直观想象)
2.理解双曲线离心率的定义、取值范围和渐近线方程. (逻辑推理)
3.通过具体实例初步了解直线与双曲线相交的相关问题.(数学运算)
已知双曲线C的方程 ,根据这个方程完成下列任务:
(1)已观察方程中x与y是否有取值范围,由此指出双曲线C在平面 直角坐标系中的位置特征;
(2)指出双曲线C是否关于x 轴、y 轴、原点对称;
(3)指出双曲线C与坐标轴是否有交点,如果有,求出交点坐标;
(4)如果 (x,y) 满足双曲线C的方程,说出当|x|增大时,ly| 怎样变化, 并指出反应了双曲线的形状具有什么特点.
一般地,如果双曲线C的标准方程 (a>0,b>0), 可得到双曲线的 几何性质为
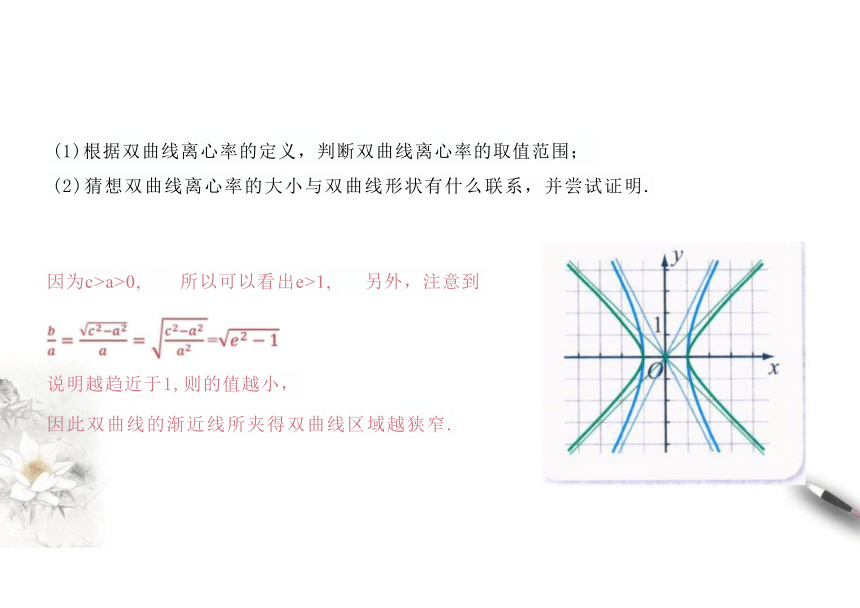
因为c>a>0, 所以可以看出e>1, 另外,注意到
说明越趋近于1,则的值越小,
因此双曲线的渐近线所夹得双曲线区域越狭窄.
(1)根据双曲线离心率的定义,判断双曲线离心率的取值范围;
(2)猜想双曲线离心率的大小与双曲线形状有什么联系,并尝试证明.
思考
(1)双曲线的离心率对开口大小有怎样的影响
提 示:双曲线的离心率
反映了双曲线开口的大小,e 越大,双曲线的开口就越大.
(2)一条直线与双曲线的渐近线平行时,它与双曲线有几个公共点
提示:1个.
那么该双曲线的范围、对称性、顶点、渐近线、离心率中,
那些与焦点在x轴上的双曲线是有区别的
如果双曲线C的标准方程是
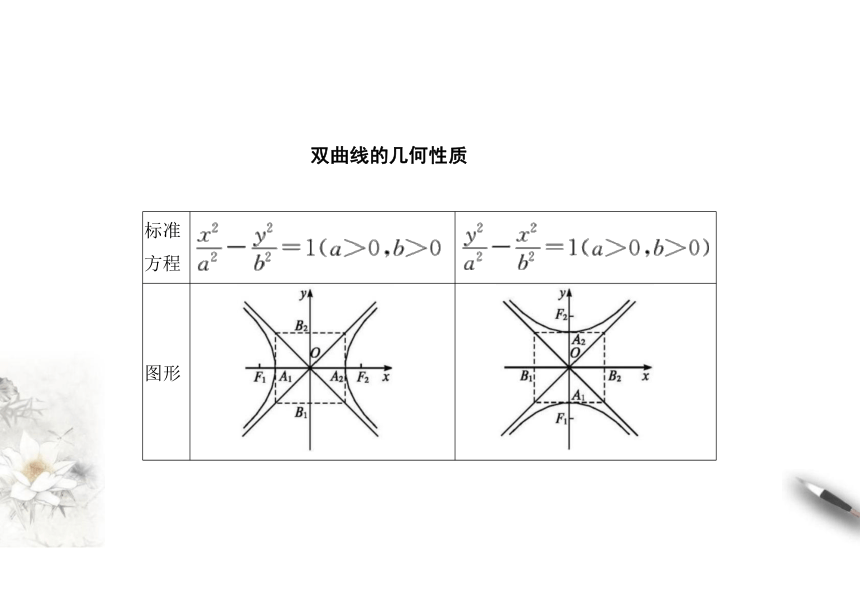
标准 方程
图形
双曲线的几何性质
标准方程
性 质 范围 x≤-a或x≥a y∈R -a或y≥a x∈R
对称性 对称轴:x轴、y轴;对称中心:坐标原点
顶点坐标 A (-a
轴 实轴:线段A,A,, 长 :2a 虚轴:线段B B , 长 :2b; 半实轴长:a,半虚轴长:b
渐近线
离心率 e = , e ∈ ( 1 , + ) , 其 中 c = √ a + b
a,b,c间的关 系 c =a +b
双曲线
椭圆
曲线 两支曲线
封闭的曲线
顶点 两个顶点
四个顶点
轴 实、虚轴
长、短轴
渐近线 有渐近线
无渐近线
离心率 e>1
0a,b,c关系 a +b =c
a -b =c
(2)等轴双曲线是实轴和虚轴等长的双曲线,它的渐近线方程是 y=±x,离心率为√2 .
(3)共轭双曲线:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线 叫做原双曲线的共轭双曲线.
(1)双曲线与椭圆的六个不同点:
1.判断
(1)双曲 的形状相同. ( )
(2)双曲 的渐近线相同. ( ) :
(3)等轴双曲线的渐近线互相垂直. ( )
答案:(1) √ (2)×(3) √
1
的离心率e=2,说明曲线是双曲线,
解得m=-35.
所以m<-8,. ∴
答案:B
的离心率e=2,则实数m 的值为( )
A.-5 B.-35 C.19 D.-11
解析:由圆锥曲
2
2.圆锥曲
例1求双曲线9y -4x =-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率、
渐近线方程.
解:将9y -4x =-36化为标准方程为
所以a=3,b=2,c= √ 13.
因此顶点坐标为(-3,0),(3,0),
焦点坐标为(- √13,0),( √13,0),
实轴长2a=6, 虚轴长2b=4,
离心率
渐近线方程为
由双曲线的方程研究其几何性质的注意点
(1)把双曲线方程化为标准形式是解决此类题的关键.
(2)由标准方程确定焦点位置,确定a,b 的值.
(3)由c =a +b 求出c的值,从而写出双曲线的几何性质.
跟踪训练1 求双曲线nx -my =mn(m>0,n>0)的半实轴长、半虚轴长、 焦点坐标、离心率、顶点坐标和渐近线方程.
解:把方程nx -my =mn(m>0,n>0)
化为标准方程为
由此可知,半实轴长a=√m,
半虚轴长b=√n,c=√m+n,
焦点坐标为( √m+n,0),(- √m+n,0),
离心率
顶点坐标为(- √m,0),(√m,0),
所以渐近线方程为 即
例2根据以下条件,求双曲线的标准方程.
(1)过点P(3,- √5),离心率为 √2;
(2)与椭 有公共焦点,且离心率
(3)与双曲 有共同渐近线,且过点(-3,2 √3).
解:(1)若双曲线的焦点在x 轴上,设其方程 ∵e=√2, ∴ ,即a =b .
又双曲线过P(3,-√5),∴ 2
由①②得a =b =4, 故双曲线方程为
若双曲线的焦点在y 轴上,
设其方程为
同理有a =b ,
由③④得a =b =-4 (舍去).综上,双曲线的标准方程为
①
②
③ ④
(2)由椭圆方 ,知半焦距为 √9-4= √5, ∴焦点是F (-√5,0),F (√5,0).
因此双曲线的焦点为(- √5,0),( √5,0).
设双曲线方程为
由已知条件,有 解得
∴所求双曲线的标准方程为
(3)设所求双曲线方程为 将点(-3,2 √3)代入得
∴双曲线方程为
即双曲线的标准方程为
(组),但要注意焦点的位置,从而正确选择方程的形式.
2.巧设双曲线方程的六种方法与技巧
(1)焦点在x 轴上的双曲线的标准方程可设
(2)焦点在y 轴上的双曲线的标准方程可设
(3)与双曲 共焦点的双曲线方程
具有相同渐近线的双曲线方程可设为
(5)渐近线为y=±kx的双曲线方程可设为k x -y =λ(λ≠0).
(6)渐近线为ax±by=0 的双曲线方程可设为a x -b y =λ(λ≠0).
.
1.根据双曲线的某些几何性质求双曲线的标准方程,一般用待定系数法转化为解方程
跟踪训练2 求适合下列条件的双曲线的标准方程.
(1)焦点在x 轴上,虚轴长为8,离心率为
(2)过点(2,0),与双曲 离心率相等.
2b=8,
从 而b=4.
代入c =a +b ,得a =9,
故双曲线的标准方程为
(2)由题意知,所求双曲线的焦点在x 轴上, 故可设其方程为
将点(2,0)的坐标代入方程得 故所求双曲线的标准方程为
解:(1)设所求双曲线的标准方程 由题意知
1.双曲线mx +y =1的虚轴长是实轴长的2倍,则m的值为( )
A.4 B.-4 C. 口
解析:由双曲线方程mx +y =1,知m<0,
则双曲线方程可化为
∴b=2,∴ ,∴ 故选C.
答案:C
则a =1,a=1, 又虚轴长是实轴长的2倍,
2. (多选)若双曲线C 的一个焦点F(5,0),P 是双曲线上一点,且渐近线 方程为 则下列结论正确的是( )
A.C 的方程
B.C的离心率为
C.焦点到渐近线的距离为3
D. |PF的|最小值为2
解析:双曲线C 的一个焦点F(5,0),且渐近线方程为 可 得 c=5, 焦点坐标在x 轴上,
所) 因为c=5,所以b=4,a=3,
所以C 的方程为 ,A 正确;
离心率为 不正确;
焦点到渐近线的距离为 ,C 不正确;
|PF|的最小值为c-a=2,D 正确.
答案:AD
3.中心在原点,焦点在x轴上,且一个焦点在直线3x-4y+12=0上的等 轴双曲线的方程是
解析:令y=0,得x=-4,
∴等轴双曲线的一个焦点为(-4,0),
故等轴双曲线的方程为x -y =8. 答案:x -y =8
4.关于双曲线 ,有以下说法:
①实轴长为6;②双曲线的离心率 焦点坐标为(±5,0);④渐近 线方程是 )焦点到渐近线的距离等于3.
正确的说法是 . (把所有正确说法的序号都填上)
解析:∵双曲线
艮 , ∴a=4,b=3,c=√9+16=5,
∴①实轴长为2a=8, 故①错误;
②双曲线的离心率是 故②正确;
③焦点坐标为F(0,±5), 故③错误;
④渐近线方程是 故④正确;
⑤焦点到渐近线的距离为 故⑤正确.
答案:②④⑤
5.已知F 为双曲线 的左焦点,P,Q为双曲线C 同一支上 的两点.若PQ 的长等于虚轴长的2倍,点A(√ 13,0)在线段PQ 上,则 △PQF 的周长为
解析:根据题意,双曲线 的左焦点F(-√ 13,0), 所以点
A( √ 13,0)是双曲线的右焦点,P,Q 为双曲线C 为6,所以|PQ I=12.
双曲线图像如图.
|PF|-|AP|=2a=4,①
IQFI-IQA|=2a=4,②
①+②得|PF|+IQF|-|PQI=8,
∴周长为|PF|+IQF|+|PQI=8+2|PQI=32. 答案:32
右支上的两点.虚轴长
6.已知双曲线
(1)求与双曲线C 有相同的焦点,且过点P(4,√3)的双曲线C 的标准 方程;
(2)直线l:y=x+m分别交双曲线C 的两条渐近线于A,B两点,当OA · OB=3时,求实数m的值.
解:(1)双曲线C 的焦点坐标为( √5,0),(-√5,0),
设双曲线C 的标准方程为 则 解
∴双曲线C 的标准方程为
(2)双曲线C 的渐近线方程为y=2x,y=-2x,
由 可得x=m,y=2m,∴A(m,2m).
由 可得
∵OA·OB=3,
∴m =3,即m=±√3.
范围
对称性 顶点
渐近线 离心率
双曲线的几何性质
应用
人教2019B版选择性必修第一册
第二章平面解析几何
2.6.2双曲线的几何性质(1)
1.掌握双曲线的简单几何性质. (直观想象)
2.理解双曲线离心率的定义、取值范围和渐近线方程. (逻辑推理)
3.通过具体实例初步了解直线与双曲线相交的相关问题.(数学运算)
已知双曲线C的方程 ,根据这个方程完成下列任务:
(1)已观察方程中x与y是否有取值范围,由此指出双曲线C在平面 直角坐标系中的位置特征;
(2)指出双曲线C是否关于x 轴、y 轴、原点对称;
(3)指出双曲线C与坐标轴是否有交点,如果有,求出交点坐标;
(4)如果 (x,y) 满足双曲线C的方程,说出当|x|增大时,ly| 怎样变化, 并指出反应了双曲线的形状具有什么特点.
一般地,如果双曲线C的标准方程 (a>0,b>0), 可得到双曲线的 几何性质为
因为c>a>0, 所以可以看出e>1, 另外,注意到
说明越趋近于1,则的值越小,
因此双曲线的渐近线所夹得双曲线区域越狭窄.
(1)根据双曲线离心率的定义,判断双曲线离心率的取值范围;
(2)猜想双曲线离心率的大小与双曲线形状有什么联系,并尝试证明.
思考
(1)双曲线的离心率对开口大小有怎样的影响
提 示:双曲线的离心率
反映了双曲线开口的大小,e 越大,双曲线的开口就越大.
(2)一条直线与双曲线的渐近线平行时,它与双曲线有几个公共点
提示:1个.
那么该双曲线的范围、对称性、顶点、渐近线、离心率中,
那些与焦点在x轴上的双曲线是有区别的
如果双曲线C的标准方程是
标准 方程
图形
双曲线的几何性质
标准方程
性 质 范围 x≤-a或x≥a y∈R -a或y≥a x∈R
对称性 对称轴:x轴、y轴;对称中心:坐标原点
顶点坐标 A (-a
轴 实轴:线段A,A,, 长 :2a 虚轴:线段B B , 长 :2b; 半实轴长:a,半虚轴长:b
渐近线
离心率 e = , e ∈ ( 1 , + ) , 其 中 c = √ a + b
a,b,c间的关 系 c =a +b
双曲线
椭圆
曲线 两支曲线
封闭的曲线
顶点 两个顶点
四个顶点
轴 实、虚轴
长、短轴
渐近线 有渐近线
无渐近线
离心率 e>1
0
a -b =c
(2)等轴双曲线是实轴和虚轴等长的双曲线,它的渐近线方程是 y=±x,离心率为√2 .
(3)共轭双曲线:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线 叫做原双曲线的共轭双曲线.
(1)双曲线与椭圆的六个不同点:
1.判断
(1)双曲 的形状相同. ( )
(2)双曲 的渐近线相同. ( ) :
(3)等轴双曲线的渐近线互相垂直. ( )
答案:(1) √ (2)×(3) √
1
的离心率e=2,说明曲线是双曲线,
解得m=-35.
所以m<-8,. ∴
答案:B
的离心率e=2,则实数m 的值为( )
A.-5 B.-35 C.19 D.-11
解析:由圆锥曲
2
2.圆锥曲
例1求双曲线9y -4x =-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率、
渐近线方程.
解:将9y -4x =-36化为标准方程为
所以a=3,b=2,c= √ 13.
因此顶点坐标为(-3,0),(3,0),
焦点坐标为(- √13,0),( √13,0),
实轴长2a=6, 虚轴长2b=4,
离心率
渐近线方程为
由双曲线的方程研究其几何性质的注意点
(1)把双曲线方程化为标准形式是解决此类题的关键.
(2)由标准方程确定焦点位置,确定a,b 的值.
(3)由c =a +b 求出c的值,从而写出双曲线的几何性质.
跟踪训练1 求双曲线nx -my =mn(m>0,n>0)的半实轴长、半虚轴长、 焦点坐标、离心率、顶点坐标和渐近线方程.
解:把方程nx -my =mn(m>0,n>0)
化为标准方程为
由此可知,半实轴长a=√m,
半虚轴长b=√n,c=√m+n,
焦点坐标为( √m+n,0),(- √m+n,0),
离心率
顶点坐标为(- √m,0),(√m,0),
所以渐近线方程为 即
例2根据以下条件,求双曲线的标准方程.
(1)过点P(3,- √5),离心率为 √2;
(2)与椭 有公共焦点,且离心率
(3)与双曲 有共同渐近线,且过点(-3,2 √3).
解:(1)若双曲线的焦点在x 轴上,设其方程 ∵e=√2, ∴ ,即a =b .
又双曲线过P(3,-√5),∴ 2
由①②得a =b =4, 故双曲线方程为
若双曲线的焦点在y 轴上,
设其方程为
同理有a =b ,
由③④得a =b =-4 (舍去).综上,双曲线的标准方程为
①
②
③ ④
(2)由椭圆方 ,知半焦距为 √9-4= √5, ∴焦点是F (-√5,0),F (√5,0).
因此双曲线的焦点为(- √5,0),( √5,0).
设双曲线方程为
由已知条件,有 解得
∴所求双曲线的标准方程为
(3)设所求双曲线方程为 将点(-3,2 √3)代入得
∴双曲线方程为
即双曲线的标准方程为
(组),但要注意焦点的位置,从而正确选择方程的形式.
2.巧设双曲线方程的六种方法与技巧
(1)焦点在x 轴上的双曲线的标准方程可设
(2)焦点在y 轴上的双曲线的标准方程可设
(3)与双曲 共焦点的双曲线方程
具有相同渐近线的双曲线方程可设为
(5)渐近线为y=±kx的双曲线方程可设为k x -y =λ(λ≠0).
(6)渐近线为ax±by=0 的双曲线方程可设为a x -b y =λ(λ≠0).
.
1.根据双曲线的某些几何性质求双曲线的标准方程,一般用待定系数法转化为解方程
跟踪训练2 求适合下列条件的双曲线的标准方程.
(1)焦点在x 轴上,虚轴长为8,离心率为
(2)过点(2,0),与双曲 离心率相等.
2b=8,
从 而b=4.
代入c =a +b ,得a =9,
故双曲线的标准方程为
(2)由题意知,所求双曲线的焦点在x 轴上, 故可设其方程为
将点(2,0)的坐标代入方程得 故所求双曲线的标准方程为
解:(1)设所求双曲线的标准方程 由题意知
1.双曲线mx +y =1的虚轴长是实轴长的2倍,则m的值为( )
A.4 B.-4 C. 口
解析:由双曲线方程mx +y =1,知m<0,
则双曲线方程可化为
∴b=2,∴ ,∴ 故选C.
答案:C
则a =1,a=1, 又虚轴长是实轴长的2倍,
2. (多选)若双曲线C 的一个焦点F(5,0),P 是双曲线上一点,且渐近线 方程为 则下列结论正确的是( )
A.C 的方程
B.C的离心率为
C.焦点到渐近线的距离为3
D. |PF的|最小值为2
解析:双曲线C 的一个焦点F(5,0),且渐近线方程为 可 得 c=5, 焦点坐标在x 轴上,
所) 因为c=5,所以b=4,a=3,
所以C 的方程为 ,A 正确;
离心率为 不正确;
焦点到渐近线的距离为 ,C 不正确;
|PF|的最小值为c-a=2,D 正确.
答案:AD
3.中心在原点,焦点在x轴上,且一个焦点在直线3x-4y+12=0上的等 轴双曲线的方程是
解析:令y=0,得x=-4,
∴等轴双曲线的一个焦点为(-4,0),
故等轴双曲线的方程为x -y =8. 答案:x -y =8
4.关于双曲线 ,有以下说法:
①实轴长为6;②双曲线的离心率 焦点坐标为(±5,0);④渐近 线方程是 )焦点到渐近线的距离等于3.
正确的说法是 . (把所有正确说法的序号都填上)
解析:∵双曲线
艮 , ∴a=4,b=3,c=√9+16=5,
∴①实轴长为2a=8, 故①错误;
②双曲线的离心率是 故②正确;
③焦点坐标为F(0,±5), 故③错误;
④渐近线方程是 故④正确;
⑤焦点到渐近线的距离为 故⑤正确.
答案:②④⑤
5.已知F 为双曲线 的左焦点,P,Q为双曲线C 同一支上 的两点.若PQ 的长等于虚轴长的2倍,点A(√ 13,0)在线段PQ 上,则 △PQF 的周长为
解析:根据题意,双曲线 的左焦点F(-√ 13,0), 所以点
A( √ 13,0)是双曲线的右焦点,P,Q 为双曲线C 为6,所以|PQ I=12.
双曲线图像如图.
|PF|-|AP|=2a=4,①
IQFI-IQA|=2a=4,②
①+②得|PF|+IQF|-|PQI=8,
∴周长为|PF|+IQF|+|PQI=8+2|PQI=32. 答案:32
右支上的两点.虚轴长
6.已知双曲线
(1)求与双曲线C 有相同的焦点,且过点P(4,√3)的双曲线C 的标准 方程;
(2)直线l:y=x+m分别交双曲线C 的两条渐近线于A,B两点,当OA · OB=3时,求实数m的值.
解:(1)双曲线C 的焦点坐标为( √5,0),(-√5,0),
设双曲线C 的标准方程为 则 解
∴双曲线C 的标准方程为
(2)双曲线C 的渐近线方程为y=2x,y=-2x,
由 可得x=m,y=2m,∴A(m,2m).
由 可得
∵OA·OB=3,
∴m =3,即m=±√3.
范围
对称性 顶点
渐近线 离心率
双曲线的几何性质
应用
