2.6.2 双曲线的几何性质(2) 课件(共24张PPT)-人教B版高中数学选择性必修第一册-教案课件习题试卷-高中数学人教版B版选择性必修第一册
文档属性
| 名称 | 2.6.2 双曲线的几何性质(2) 课件(共24张PPT)-人教B版高中数学选择性必修第一册-教案课件习题试卷-高中数学人教版B版选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 22:12:52 | ||
图片预览



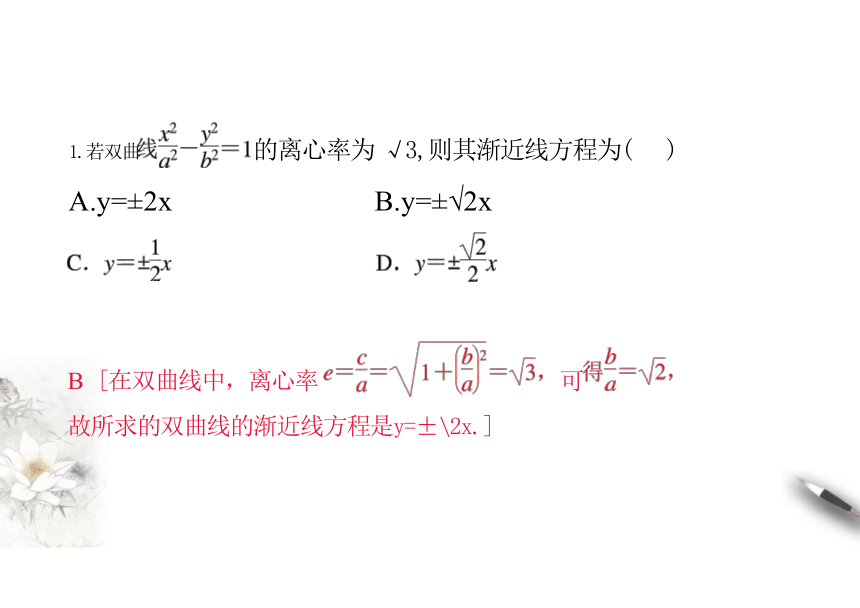



文档简介
(共24张PPT)
人教2019B版选择性必修第一册
第二章平面解析几何
2.6.2双曲线的几何性质(2)
1.掌握双曲线的简单几何性质
2.理解双曲线离心率的意义及算法.
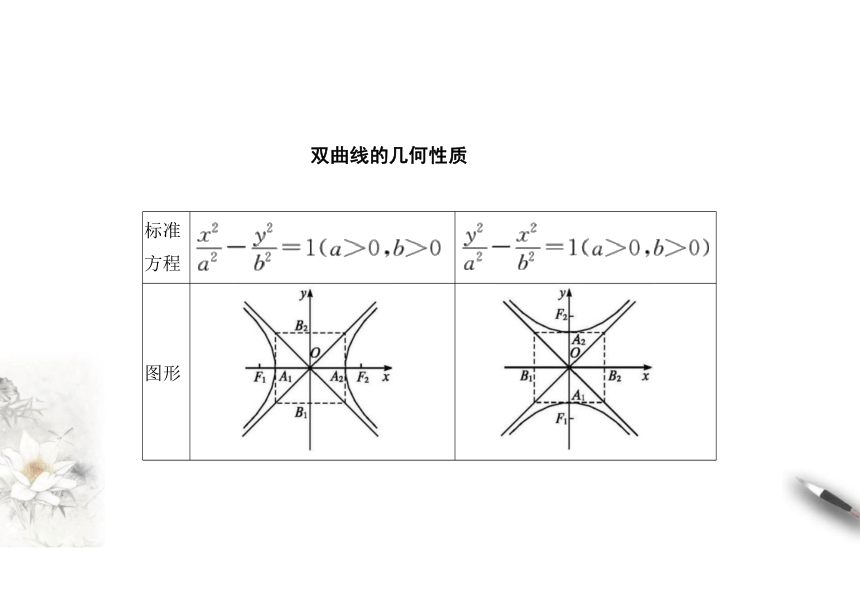
标准 方程
图形
双曲线的几何性质
标准方程
性 质 范围 x≤-a或x≥a y∈R -a或y≥a x∈R
对称性 对称轴:x轴、y轴;对称中心:坐标原点
顶点坐标 A (-a
轴 实轴:线段A,A,, 长 :2a 虚轴:线段B B ,长 :2b; 半实轴长:a,半虚轴长:b
渐近线
离心率 e = , e ∈ ( 1 , + ) , 其 中 c = √ a + b
a,b,c间的关 系 c =a +b
B [在双曲线中,离心率 可 故所求的双曲线的渐近线方程是y=±\2x.]
1.若双曲 的离心率为 √3,则其渐近线方程为( )
A.y=±2x B.y=±√2x
2.若双曲线 的一条渐近线经过点(3,—4),则此双曲线的 离心率为( )
A. B. C. D.
[思路探究] 渐近线经过点(3,—4)→渐近线的斜率→离心率.
[解析] ( 1)由题意知
所以
解 析 : 设 双 曲 线 方 程
不 妨 设 点M 在 双 曲 线 的 右 支 上 , 如 图 ,
AB=BM=2a,∠MBA=120°,
作MH⊥x轴于H, 则∠MBH=60°,BH=a,MH=√3a,
所以M(2a, √3a).
将点M 的坐标代入双曲线方程 得a=b, 所以e=√2.故选D.
3.已知A,B 为双曲线E的左、右顶点,点M在E 上,△ABM为等腰三角形,且顶角为120°,
则E 的离心率为( )
A. B.2 C. D.
例 1双曲线方程 ,其中a>0, 双曲线的渐近线与圆
(x-2) +y =1相切,则双曲线的离心率为( )
B.√3 C.√2 D
解析:根据题意,可以求得双曲线的渐近线的方程为x±ay=0,而 圆(x-
2) +y =1 的圆心为(2,0),半径为1,结合题意 结 合a>0 的
条件,求得a= √3, 所以c= √3+1=2, 所以有 故选A.
答案:A
A
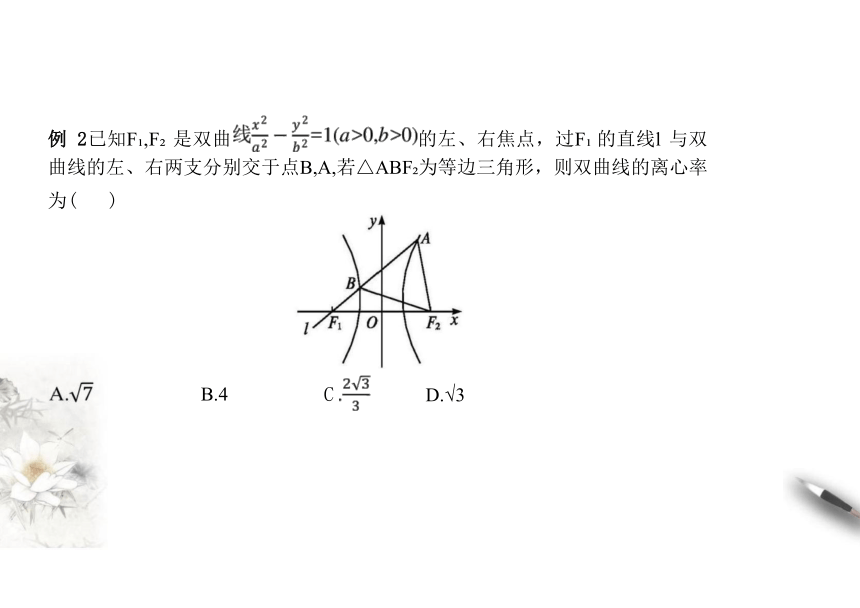
例 2已知F ,F 是双曲 的左、右焦点,过F 的直线l 与双 曲线的左、右两支分别交于点B,A,若△ABF 为等边三角形,则双曲线的离心率
C D.√3
为( )
B.4
解析:因为△ABF 为等边三角形,所以|AB|=|BF I=|AF I ,因为A 为双曲线右支上一点,
所以 |F A|-|F A|=|F A|-|AB|=|F B|=2a,
因 为B 为双曲线左支上一点,
所以|BF I-|BF |=2a, 所以|BF |=4a,
由 ∠ABF =60°, 得∠F BF =120°, 在△F BF 中,由余弦
定理得4c =4a +16a -2·2a.4a·cos
e =7, 又e>1, 所以e=√7. 故选A.
答案:A
120°,得c =7a , 则
双曲线的弦,如果∠PF Q=90°, 求双曲线的离心率.
(a>0,b>0) 的两个焦点,PQ是经过F 且垂直于x轴的
例3.已 知F ,F 是双曲线
那么
由|PF I=|QF I,∠PF Q=90°,知|PF I=|F F ],
所) 所以b =2ac,
即 e -2e-1=0,
所以e=1+ √2 或e=1- √2(舍去), 所以双曲线的离心率为1+ √2.
解:设F (-c,0)(c>0),将x=-c 代入双曲线的方程
所以c -2ac-a =0,所以
重
求双曲线的离心率
(1)求双曲线的离心率或其范围的方法
①求 a,b,c 的值,由 直接求e.
②列出含有a,b,c的齐次方程或不等式,借助于b =c -a 消 去b,然后转 化成关于e的方程或不等式求解.
(2)求解时,若用到特殊几何图形,可运用几何性质使问题简化.
解析:因为双曲线的渐近线方程为x±y=0, 所以a=b=1.
所 以c=√a +b = √2, 双曲线的率心率
跟踪训练1 渐近线方程为x±y=0 的双曲线的离心率是( )
答案:C
C.√2
D.2
B.1
A
A.
垂
跟踪训练2已知点F(1,0).若 l:x=-1与双曲
两条渐近线分别交于点A 和 点B, 且 A|B|=4|OF|(O 为原点),则双曲 线的离心率为( )
A.√2 B.√3 C.2 D.√5
解析:由 得
由 得 事
由|AB|=4|OF|得 2
故选D.
答案:D
。
【答案】D [由题意得
∴√a +3=2a,
∴a +3=4a ,∴a =1,∴a=1.]
1. 已知双曲 的离心率为2,则a=( )
A.2
D.1
C.
B.
2.若一双曲线与椭圆4x +y =64 有公共的焦点,且它们的离心率互为倒数,
则该双曲线的方程为( )
A.y —3x =36 B.x —3y =36
C.3y —x =36 D.3x —y =36
离心率 则双曲线的焦点在y 轴上,c=43,
从而a=6,b =12, 故所求双曲线的方程为y —3x =36.]
【答案】A [椭圆4x +y =64, 即 焦点为(0,±4 √3),
3.已知a>b>0, 椭 圆C 的方程 双曲线C 的 方 程
与 C 的离心率之积 则 C 的渐近线方程为( )
A.x±√2y=0 B.√2x±y=0
C.x±2y=0 D.2x±y=0
所以双曲线C 的渐近线方程是
[解] 椭圆C 的离心率
双曲线C 的离心率
即x± √2y=0.
解
所
由
4 . 设F ,F 分别为双曲: ,b>0) 的左、右焦点,双曲线上存在
一 点P 使得 P|F I+|PF I=3b, 9 则该双曲线的离心率为( )
A. B. C. D.3
B [考虑双曲线的对称性,不妨设 P 在右支上,则|PF I一|PF I=2a, 而 |PF I
+|PF I=3b, 两式等号左右两边平方后相减,得
(负值舍去).
∴该双曲线的离心率
又已知
|PF
,∴
| ·
5.过双曲线C: ,b>0)的右焦点作一条与其渐近线平行的直线,
交 C 于 点P. 若点P 的横坐标为2a, 则 C 的离心率为
2+ √3 [如图,F ,F 为双曲线C的左,右焦点,将点P 的横坐标2a
不妨令点P 的坐标为(2a, 一 √3b),
得到c=(2+ √3)a,
即双曲线C 的离心率
中,得y =3b ,
此时
6.设 F 为双曲线 的右焦点,0为坐标原点,以 OF 为直径的圆与圆x +y =a 交于P,Q 两点.若|PQI=|OF|,则C 的离 心率为( )
A.√2 B.√3 C.2 D.√5
解析:如图,设PQ 与x 轴交于点A,由对称性可知PQ⊥x轴.
∵|PQI=|OF|=c,
∴PA为以OF 为直径的圆的半径,A为圆心,
又点P 在圆x +y =a 上:
∴e=√2,故选A.
,
艮 。
,
范围
对称性 顶点
渐近线 离心率
双曲线的几何性质
应用
人教2019B版选择性必修第一册
第二章平面解析几何
2.6.2双曲线的几何性质(2)
1.掌握双曲线的简单几何性质
2.理解双曲线离心率的意义及算法.
标准 方程
图形
双曲线的几何性质
标准方程
性 质 范围 x≤-a或x≥a y∈R -a或y≥a x∈R
对称性 对称轴:x轴、y轴;对称中心:坐标原点
顶点坐标 A (-a
轴 实轴:线段A,A,, 长 :2a 虚轴:线段B B ,长 :2b; 半实轴长:a,半虚轴长:b
渐近线
离心率 e = , e ∈ ( 1 , + ) , 其 中 c = √ a + b
a,b,c间的关 系 c =a +b
B [在双曲线中,离心率 可 故所求的双曲线的渐近线方程是y=±\2x.]
1.若双曲 的离心率为 √3,则其渐近线方程为( )
A.y=±2x B.y=±√2x
2.若双曲线 的一条渐近线经过点(3,—4),则此双曲线的 离心率为( )
A. B. C. D.
[思路探究] 渐近线经过点(3,—4)→渐近线的斜率→离心率.
[解析] ( 1)由题意知
所以
解 析 : 设 双 曲 线 方 程
不 妨 设 点M 在 双 曲 线 的 右 支 上 , 如 图 ,
AB=BM=2a,∠MBA=120°,
作MH⊥x轴于H, 则∠MBH=60°,BH=a,MH=√3a,
所以M(2a, √3a).
将点M 的坐标代入双曲线方程 得a=b, 所以e=√2.故选D.
3.已知A,B 为双曲线E的左、右顶点,点M在E 上,△ABM为等腰三角形,且顶角为120°,
则E 的离心率为( )
A. B.2 C. D.
例 1双曲线方程 ,其中a>0, 双曲线的渐近线与圆
(x-2) +y =1相切,则双曲线的离心率为( )
B.√3 C.√2 D
解析:根据题意,可以求得双曲线的渐近线的方程为x±ay=0,而 圆(x-
2) +y =1 的圆心为(2,0),半径为1,结合题意 结 合a>0 的
条件,求得a= √3, 所以c= √3+1=2, 所以有 故选A.
答案:A
A
例 2已知F ,F 是双曲 的左、右焦点,过F 的直线l 与双 曲线的左、右两支分别交于点B,A,若△ABF 为等边三角形,则双曲线的离心率
C D.√3
为( )
B.4
解析:因为△ABF 为等边三角形,所以|AB|=|BF I=|AF I ,因为A 为双曲线右支上一点,
所以 |F A|-|F A|=|F A|-|AB|=|F B|=2a,
因 为B 为双曲线左支上一点,
所以|BF I-|BF |=2a, 所以|BF |=4a,
由 ∠ABF =60°, 得∠F BF =120°, 在△F BF 中,由余弦
定理得4c =4a +16a -2·2a.4a·cos
e =7, 又e>1, 所以e=√7. 故选A.
答案:A
120°,得c =7a , 则
双曲线的弦,如果∠PF Q=90°, 求双曲线的离心率.
(a>0,b>0) 的两个焦点,PQ是经过F 且垂直于x轴的
例3.已 知F ,F 是双曲线
那么
由|PF I=|QF I,∠PF Q=90°,知|PF I=|F F ],
所) 所以b =2ac,
即 e -2e-1=0,
所以e=1+ √2 或e=1- √2(舍去), 所以双曲线的离心率为1+ √2.
解:设F (-c,0)(c>0),将x=-c 代入双曲线的方程
所以c -2ac-a =0,所以
重
求双曲线的离心率
(1)求双曲线的离心率或其范围的方法
①求 a,b,c 的值,由 直接求e.
②列出含有a,b,c的齐次方程或不等式,借助于b =c -a 消 去b,然后转 化成关于e的方程或不等式求解.
(2)求解时,若用到特殊几何图形,可运用几何性质使问题简化.
解析:因为双曲线的渐近线方程为x±y=0, 所以a=b=1.
所 以c=√a +b = √2, 双曲线的率心率
跟踪训练1 渐近线方程为x±y=0 的双曲线的离心率是( )
答案:C
C.√2
D.2
B.1
A
A.
垂
跟踪训练2已知点F(1,0).若 l:x=-1与双曲
两条渐近线分别交于点A 和 点B, 且 A|B|=4|OF|(O 为原点),则双曲 线的离心率为( )
A.√2 B.√3 C.2 D.√5
解析:由 得
由 得 事
由|AB|=4|OF|得 2
故选D.
答案:D
。
【答案】D [由题意得
∴√a +3=2a,
∴a +3=4a ,∴a =1,∴a=1.]
1. 已知双曲 的离心率为2,则a=( )
A.2
D.1
C.
B.
2.若一双曲线与椭圆4x +y =64 有公共的焦点,且它们的离心率互为倒数,
则该双曲线的方程为( )
A.y —3x =36 B.x —3y =36
C.3y —x =36 D.3x —y =36
离心率 则双曲线的焦点在y 轴上,c=43,
从而a=6,b =12, 故所求双曲线的方程为y —3x =36.]
【答案】A [椭圆4x +y =64, 即 焦点为(0,±4 √3),
3.已知a>b>0, 椭 圆C 的方程 双曲线C 的 方 程
与 C 的离心率之积 则 C 的渐近线方程为( )
A.x±√2y=0 B.√2x±y=0
C.x±2y=0 D.2x±y=0
所以双曲线C 的渐近线方程是
[解] 椭圆C 的离心率
双曲线C 的离心率
即x± √2y=0.
解
所
由
4 . 设F ,F 分别为双曲: ,b>0) 的左、右焦点,双曲线上存在
一 点P 使得 P|F I+|PF I=3b, 9 则该双曲线的离心率为( )
A. B. C. D.3
B [考虑双曲线的对称性,不妨设 P 在右支上,则|PF I一|PF I=2a, 而 |PF I
+|PF I=3b, 两式等号左右两边平方后相减,得
(负值舍去).
∴该双曲线的离心率
又已知
|PF
,∴
| ·
5.过双曲线C: ,b>0)的右焦点作一条与其渐近线平行的直线,
交 C 于 点P. 若点P 的横坐标为2a, 则 C 的离心率为
2+ √3 [如图,F ,F 为双曲线C的左,右焦点,将点P 的横坐标2a
不妨令点P 的坐标为(2a, 一 √3b),
得到c=(2+ √3)a,
即双曲线C 的离心率
中,得y =3b ,
此时
6.设 F 为双曲线 的右焦点,0为坐标原点,以 OF 为直径的圆与圆x +y =a 交于P,Q 两点.若|PQI=|OF|,则C 的离 心率为( )
A.√2 B.√3 C.2 D.√5
解析:如图,设PQ 与x 轴交于点A,由对称性可知PQ⊥x轴.
∵|PQI=|OF|=c,
∴PA为以OF 为直径的圆的半径,A为圆心,
又点P 在圆x +y =a 上:
∴e=√2,故选A.
,
艮 。
,
范围
对称性 顶点
渐近线 离心率
双曲线的几何性质
应用
