2-5-2 圆与圆的位置关系 课件(共62张PPT)-高中数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2-5-2 圆与圆的位置关系 课件(共62张PPT)-高中数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 22:13:48 | ||
图片预览










文档简介
(共62张PPT)
第二章直线和圆的方程
2.5 直线与圆、圆与圆的位置关系
2.5.2 圆与圆的位置关系
数学
学习指导
核心素养
1.能根据给定圆的方程,判断圆与圆 的位置关系. 2.能用直线和圆的方程解决一些简单 的问题,体会用代数方法处理几何问 题的思想.
1.数学抽象、数学运算:圆与
圆的位置关系的判断.
2.直观想象、数学运算:两圆
相交及相切的问题.
圆与圆位置关系的判定方法
(1)几何法
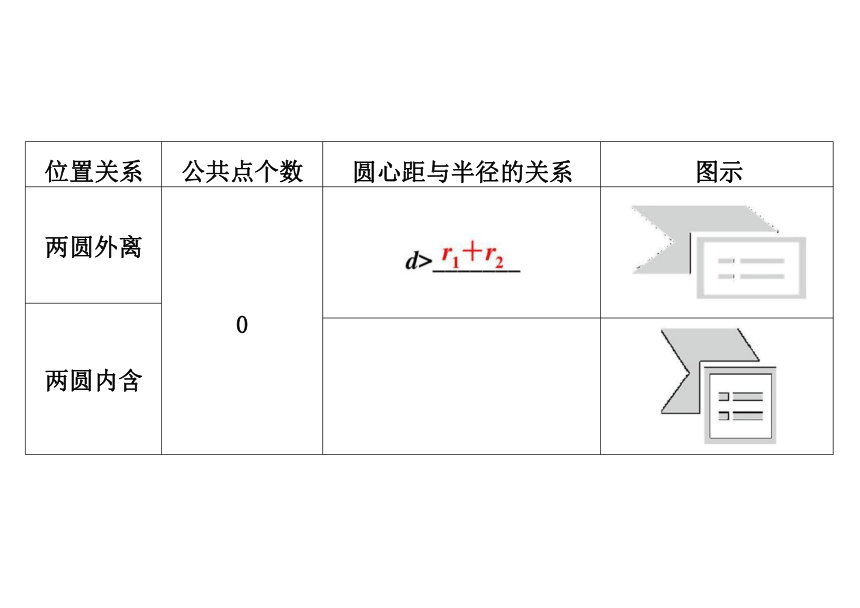
若两圆的半径分别为r ,r , 圆心距为d, 则两圆有以下位置关系:
预习案▼自主学习
[研读 导学 尝试]
位置关系 公共点个数 圆心距与半径的关系
图示
两圆外离 0
两圆内含
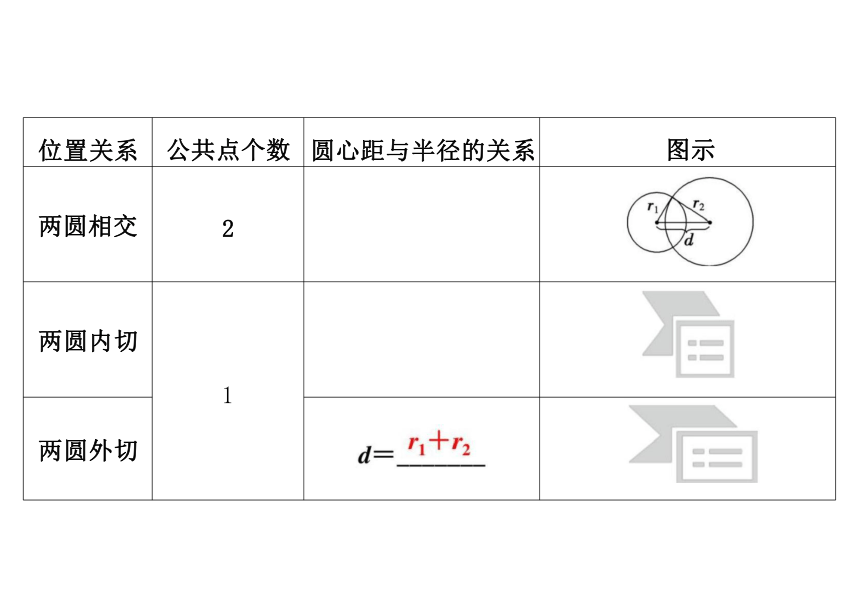
位置关系 公共点个数 圆心距与半径的关系
图示
两圆相交 2
两圆内切 1
两圆外切
(2)代数法
通过两圆方程组成的方程组的实数解的个数进行判断.
消元 一元二次方程
程
程
方
方
C
C
圆
圆
当两圆相交、外切、内切时,连心线有什么性质
提示:当两圆相交时,连心线垂直平分公共弦;
当两圆外切时,连心线垂直于过两圆公共点的公切线;
当两圆内切时,连心线垂直于两圆的公切线.
1. 判断正误(正确的打“√ ”,错误的打“×”)
(1)将两圆方程联立,若方程组有两个解,则两圆相交.( √)
(2)若两个圆没有公共点,则两圆一定外离.(×)
(3)若两圆外切,则两圆有且只有一个公共点,反之也成立.(×)
(4)若两圆有公共点,则Ir —r I≤d≤r +r .( √)
2.设圆C :x +y =1 与圆C :(x—2) +(y+2) =1, 则圆C 与C 的位置
关系是( )
A.相 交 B. 外离
C. 外 切 D. 内含
解析:根据题意,可知圆C 的圆心为C (0,0), 半 径r =1, 圆 C 的圆心
为C (2, 一2),半径r =1, 且圆C 与圆C 的圆心距d=√2 +(-2)
=22>1+1,即 d>r +r , 故两圆外离.
3.已知圆C :x +y —8x—4y+11=0 和圆C :x +y +2y-3=0, 则两
圆的公切线有( )
A.1 条 B.2 条
C.3 条 D.4 条
解析:圆C 的标准方程为(x-4) +(y-2) =9,则圆心为C (4,2), 半径
r =3;
圆C 的标准方程为x +(y+1) =4, 则圆心为C (0, 一1),半径r =2.
因为两圆的圆心距|C C I= √ (4-0) +(2+1) =5,
所以|C C I=r +r , 即圆心C 和圆C 外切,可知两圆有3条公切线。
故选C.
4.若圆C :(x+1) +(y+1) =4 与圆C :(x—2) +(y-3) =m 内切,则m
●
解析:因为圆C :(x+1) +(y+1) =4, 圆 C :(x—2) +(y—3) =m,
所以圆心距d=√(2+1) +(3+1) =5.
因为圆C 与圆C 内切,所以5=Nm —2|,所以m=49.
答案:49
探究点1 圆与圆位置关系的判断
[问题探究]
根据代数法确定两个圆的位置关系时,能否准确得出两圆的位置关系
提示:不能,如两圆方程组成的方程组有一组解,两圆外切或内切.
已知圆C :x +y —2mx+4y+m —5=0, 圆C :x +y +2x—
2my+m —3=0, 问:m 为何值时,(1)圆C 与圆C 外切 (2)圆C 与圆C 内含
【解】 对于圆C , 圆 C 的方程,
配方得C :(x—m) +(y+2) =9,
C :(x+1) +(y—m) =4.
(1)如果圆C 与圆C 外切,
则有 (m+1) +(-2-m) =3+2,
即m +3m—10=0,
解得m=—5 或 m=2.
故当m=—5 或2时,圆C 与圆C 外切.
(2)如果圆C 与圆C 内含,
则有 √(m+1) +(-2-m) <3-2,
即(m+1) +(m+2) <1, 整理得m +3m+2<0,
解得一2故当一2判断两圆的位置关系的2种方法
(1)几何法:将两圆的圆心距d与两圆的半径之差的绝对值、半径之和进
行比较,进而判断出两圆的位置关系,这是在解析几何中主要使用的方
法 .
(2)代数法:将两圆的方程组成方程组,通过解方程组,根据方程组解的
个数进而判断两圆位置关系.
= 判断下列两圆的位置关系:
(1)(x+2) +(y—2) =1 与(x—2) +(y-5) =16; (2)x +y +6x—7=0 与x +y +6y—27=0.
解:(1)根据题意,得两圆的半径分别为r =1 和 r =4,
两圆的圆心距d=√ [2-(-2)] +(5-2) =5.
因为d=r +r , 所以两圆外切.
(2)将两圆的方程化为标准方程,得(x+3) +y =16,x +(y+3) =36.
故两圆的半径分别为R=4 和r=6,
因为IR—r探究点2 两圆相切问题
例2已知圆C 与圆C :x +y —2x=0 相外切,并且与直线x+ √3 y=0
相切于点A(3,一 √3),求圆C 的方程.
【解】 设圆C 的方程为(x—a) +(y—b) =r (r>0),
因为圆C 与圆C :(x—1) +y =1 相外切,
所以 √b +(a-1) =r+1.①
又因为圆C 与直线x+ √3 y=0相切于A(3, 一 √3),
由①②③解 或
故圆C 的方程为(x—4) +y =4或x +( y+43 ) =36.
1. 若圆x +y =m 与圆x +y +6x—8y—11=0 内切,则m=
解析:圆 x +y =m 的圆心坐标为(0,0),半径 ,
圆x +y +6x—8y—11=0 的圆心坐标为(一3,4),半径 r =6.
因为两圆内切,且圆心距d=5, 所以|6- √m |=5,
解得m=1 或 m=121.
答案:1或121
2.求与圆C:(x—2) +(y+1) =4 相切于点A(4,一1)且半径为1的圆的方
程.
解:已知圆C:(x—2) +(y+1) =4 的圆心为C(2, 一 1).
设所求圆B 的圆心为B(a,b), 切点为A(4,一 1),则点C,A,B 共线.
则b=—1,
又因为 A|B|=1, 可得a=5 或3,
即圆心B 的坐标为(5,一1)或(3,一1),
故圆B的方程为(x—5) +(y+1) =1 或(x—3) +(y+1) =1.
探究点3 与两圆相交有关的问题
已知圆C :x +y +2x—6y+1=0, 圆C :x +y —4x+2y-11=
0,求两圆的公共弦所在的直线方程及公共弦长.
① 一 ②,得3x—4y+6=0.
因为A,B 两点坐标都满足此方程,
所以3x—4y+6=0 即为两圆公共弦所在直线的方程。
易知圆C 的圆心为C (一1,3),半径r=3.
【 解】 设两圆交点为 A,B, 则 A,B 两点的坐标均满足方程组
即两圆的公共弦长
又点C 到直线AB 的距离
●
(1)两圆相交时,公共弦所在的直线方程
若圆C :x +y +D x+E y+F =0 与圆C :x +y +D x+E y+F =0 相
交,则两圆公共弦所在直线的方程为(D -D )x+ (E 一E )y+F -F =0.
(2)圆系方程
一般地过圆C :x +y +D x+E y+F =0 与圆C :x +y +D x+E y+
F =0 交点的圆的方程可设为:x +y +D x+E y+F +λ(x +y +D x+ E y+F )=0(λ≠ 一1),然后再根据其他条件求出λ,即可得圆的方程.
== 求经过两圆x +y +6x—4=0 和x +y +6y—28=0 的交点
且圆心在直线x—y-4=0 上的圆的方程.
解:方法一:解方程
得两圆的交点A(—1,3),B(—6,—2).
设所求圆的圆心为(a,b), 因为圆心在直线x—y-4=0 上,故b=a—4.
解得
故圆心 9
半径为
故圆的方程
即x +y —x+7y—32=0.
方法二:因为圆x +y +6y—28=0 的圆心(0,—3)不在直线x—y—4=0
上,故可设所求圆的方程为x +y +6x—4+λ(x +y +6y—28)=0(λ≠
—1),其圆心 代入x—y-4=0, 求得λ=—7.
故所求圆的方程为x +y —x+7y—32=0.
1. 圆O :x +y -4y+3=0 与圆O :x +y —16y=0 的位置关系是( )
A. 相离 B. 相交
C. 相 切 D . 内含
解析:因 为O (0,2),r =1,O (0,8),r =8,|O O I=
(0 — 0) +(2 - 8) =6,则 |O O I2. 圆x +y =1 与圆x +y +2x+2y+1=0 的交点坐标为 ( )
A.(1,0) 和(0,1) B.(1,0) 和(0,—1)
C. (一1,0)和(0,一1) D. (一1,0)和(0,1)
解
所以两圆的交点坐标为(—1,0)和(0,—1).
解析:
3.已知圆C :(x—2) +(y-1) =10 与圆C :(x+6) +(y+3) =50 交于
A,B 两点,则AB所在的直线方程是
解析:两圆方程相减可得一16x—32—8y— 8=—40,整理得2x+ y=0.
答案:2x+y=0
4. 已知以C(3,4) 为圆心的圆与圆x +y =1 外切,求圆C的方程。
解:设圆C 的半径为r, 则 圆C 的方程为(x—3) +(y-4) =r .
由题意得两圆圆心距d= √ (3-0) +(4-0) =5,
因为两圆外切,所以圆心距等于两圆半径之和,即5=r+1, 解得r=4.
故圆C 的方程为(x—3) +(y—4) =16.
应用案▼巩固提升
[ 强 化 培 优 通关]
[A 基础达标]
1. 两圆x +y —1=0 和x +y —4x+2y—4=0 的位置关系是( )
A. 内切 B. 相交
C. 外 切 D. 外 离
解析:将两圆化成标准方程分别为x +y =1,(x—2) +(y+1) =9, 可知圆
心距d=√5, 由于22.圆x +y —2x+F=0 和圆x +y +2x+Ey—4=0 的公共弦所在的直线方
程是x—y+1=0, 则( )
A.E=—4,F=8 B.E=4,F=—8
C.E=—4,F=—8 D.E=4,F=8
得4x+Ey-4—F=0, 则 9
解得E=—4,F=— 8, 故选C.
解析:由题意联立两圆方程
。
3 . 已知圆 x +y —4x+6y=0 和圆x +y —6x=0 交于A,B 两点,则公共
弦AB 的垂直平分线的方程为( )
A.x+y+3=0 B.2x—y—5=0
C.3x—y-9=0 D.4x—3y+7=0
解析:由题意知公共弦AB 的垂直平分线即为两圆圆心连线所在的直线.
两圆的圆心分别为(2,—3),(3,0),
所以所求直线的斜率 故直线方程为3x—y—9=0.
4.已知圆M:(x—a) +y =4(a>0) 与圆N:x +(y—1) =1 外切,则直线x
-y- √2 =0被圆M 截得的线段的长度为( )
A.1 B.√
C.2
解析:由题意,知√a +1 =2+1,a>0,
所以 a=2√2, 圆心 M(22,0) 到直线 x—y-√2=0 的距离 d=
所以直线x-y- √2=0 被圆M 截得的线段的长度为2/4-1 =2\3,故
选D.
5.(多选)已知半径为1的动圆与圆(x—5) +(y+7) =16相切,则动圆圆心
的轨迹方程是( )
A.(x—5) +(y—7) =25
B.(x—5) +(y—7) =17
C/(x—5) +(y+7) =9
D/(x-5) +(y+7) =25
解析:设动圆圆心为(x,y),若动圆与已知圆外切,则√(x-5) +(y+7)
=4+1,
所 以(x —5) +(y+7) =25; 若 动 圆 与 已 知 圆 内 切 , 则
所以(x—5) +(y+7) =9.
6. 若圆x +y —2ax+a =2 和x +y —2by+b =1 外离,则a,b 满足的条
件是 ●
解析:由题意可得两圆圆心坐标和半径长分别为(a,0),√2 和(0,b),1,
因为两圆相离,所以 √a +b >12 +1,
即a +b >3+2 √2.
答案:a +b >3+2 √2
7. 若点A(a,b) 在圆x +y =4 上,则圆(x—a) +y =1 与圆x +(y—b) =1
的位置关系是 ●
解析:因为点A(a,b)在圆x +y =4 上,所以a +b =4.
又圆x +(y—b) =1 的圆心C (0,b), 半径 r =1,
圆(x—a) +y =1的圆心C (a,0),半径r =1,
则圆心距d=|C C I=√a +b =√4 =2=r +r ,
所以两圆外切.
答案:外切
8. 以(3,—4)为圆心,且与圆x +y =64 内切的圆的方程是
解析:圆x +y =64 的圆心为(0,0),半径r =8,
所以圆心距 d=√3 +4 =5,
设所求圆半径为r,则 |r—r'=d,
所以|r—8|=5,
所以r=3 或r=13.
所以圆的方程为(x—3) +(y+4) =9或(x—3) +(y+4) =169.
答案:(x—3) +(y+4) =9或(x—3) +(y+4) =169
9.已知圆C :x +y —2mx+4y+m —5=0 与圆C :x +y +2x=0.
(1)当m=1 时,判断圆C 与圆C 的位置关系;
(2)是否存在m 使得圆C 与圆C 内含
解:(1)因为m=1, 所以两圆的方程分别可化为C :(x—1) +(y+2) =9,
C :(x+1) +y =1.
又因为r +r =3+1=4,r —r =3—1=2,
所以圆C 与圆C 相交.
所以r —r(2)假设存在m 使得圆C 与圆C 内含,
则 √(m+1) +(-2-0) <3-1,
即(m+1) <0, 显然该不等式无解.
故不存在m 使得圆C 与圆C 内含.
10.(2021·吉林省高一期末)已知圆M:x +y —2ay=0(a>0)截直线x+y=0
所得线段的长度是2 √2,判断圆M 与圆N:(x—1) +(y—1) =1的位置关 系。
解:把圆M 的方程化为标准方程为x +(y—a) =a ,
所以M(0,a),r =a.
所以点M 到直线x+y=0 的距离
由题意可得, +2=a , 所 以a=2,
所以M(0,2),r =2. 又N(1,1),r =1,
所以|MN|=√2, 所以|r —r k|MN所以两圆相交.
[B 能力提升]
11.已知点M 在圆C :(x+3) +(y—1) =4 上,点N 在圆C :(x—1) +(y
十2) =4上,则|MNI的最大值是( )
A.5 B.7
C.9 D.11
解析:由题意知圆C 的圆心C (一3,1),半径长r =2; 圆 C 的圆心C (1,
—2),半径长r =2.
因为两圆的圆心距
所以两圆相离,从而|MNI 的最大值为d +r +r =5+2+2= 9.故选C.
12.过圆 x +y —x—y—2=0与圆x +y +4x—4y—8=0 的交点和点(3,1)
的圆的方程是 ●
解析:设所求圆方程为 x +y —x—y—2+λ(x +y +4x—4y—8)=0,将(3,
1)代入得 .故所求圆的方程为
答案:
13.若⊙0: x +y =5 与⊙O :(x—m) +y =20(m∈R) 相交于A,B 两点
且两圆在点A 处的切线互相垂直,则线段AB的长度为 ●
解析:如图所示,在Rt△00 A 中 ,OA=√5,O A=2√ ,
所以AB=4.
答案:4
所以00 =5,
14. 已知圆O 的方程为x +(y+1) =4, 圆 O 的圆心为O (2,1).
(1)若圆O 与圆O 外切,求圆O 方程;
(2)若圆O 与圆O 交于A,B 两点,且AB|=2 √2, 求圆O 的方程.
解:(1)设圆O 、圆O 的半径分别为r ,r , 则r =2.
因为两圆外切,所以|O O I=r +r ,
所以圆O 的方程是(x—2) +(y-1) =12-82.
圆 O ,O 的方程相减,即得两圆公共弦AB 所在直线的方程,为4x+4y+
r3-8=0.
所以圆心 O (0, 一1)到直线AB 的距离
√ 2,解得r =4 或r3=20.
所以圆O 的方程为(x—2) +(y-1) =4 或(x—2) +(y—1) =20.
[C 拓展探究]
15. 已知动点P 到两个定点0(0,0),A(3,0) 的距离的比为 ●
(1)求动点P 的轨迹C 的方程;
(2)已知圆Q 的圆心为 Q(t,t)(t>0),且圆Q 与 x 轴相切,若圆 Q 与曲线C
有公共点,求实数t 的取值范围.
解:(1)设P(x,y), 则 |AP|=2|OP|,
即|APl =4|OPP ,
所以(x—3) +y =4(x +y ),
整理得(x+1) +y =4.
所以动点P 的轨迹C 的方程为(x+1) +y =4.
(2)因为点Q 的坐标为(t,t)(t>0),且 圆Q 与x 轴相切,所以圆Q 的半径为t,
所以,圆Q 的方程为(x—t) +(y—t) =t.
因为圆Q 与圆C 有公共点,
又圆Q 与圆C 的圆心距为
所以|2—t|≤|CQI≤2+t,
即(2—t) ≤2t +2t+1≤(2+t) ,
解得 — 3+23 ≤t≤3.
所以,实数t的取值范围是[-3+2\3,3].
第二章直线和圆的方程
2.5 直线与圆、圆与圆的位置关系
2.5.2 圆与圆的位置关系
数学
学习指导
核心素养
1.能根据给定圆的方程,判断圆与圆 的位置关系. 2.能用直线和圆的方程解决一些简单 的问题,体会用代数方法处理几何问 题的思想.
1.数学抽象、数学运算:圆与
圆的位置关系的判断.
2.直观想象、数学运算:两圆
相交及相切的问题.
圆与圆位置关系的判定方法
(1)几何法
若两圆的半径分别为r ,r , 圆心距为d, 则两圆有以下位置关系:
预习案▼自主学习
[研读 导学 尝试]
位置关系 公共点个数 圆心距与半径的关系
图示
两圆外离 0
两圆内含
位置关系 公共点个数 圆心距与半径的关系
图示
两圆相交 2
两圆内切 1
两圆外切
(2)代数法
通过两圆方程组成的方程组的实数解的个数进行判断.
消元 一元二次方程
程
程
方
方
C
C
圆
圆
当两圆相交、外切、内切时,连心线有什么性质
提示:当两圆相交时,连心线垂直平分公共弦;
当两圆外切时,连心线垂直于过两圆公共点的公切线;
当两圆内切时,连心线垂直于两圆的公切线.
1. 判断正误(正确的打“√ ”,错误的打“×”)
(1)将两圆方程联立,若方程组有两个解,则两圆相交.( √)
(2)若两个圆没有公共点,则两圆一定外离.(×)
(3)若两圆外切,则两圆有且只有一个公共点,反之也成立.(×)
(4)若两圆有公共点,则Ir —r I≤d≤r +r .( √)
2.设圆C :x +y =1 与圆C :(x—2) +(y+2) =1, 则圆C 与C 的位置
关系是( )
A.相 交 B. 外离
C. 外 切 D. 内含
解析:根据题意,可知圆C 的圆心为C (0,0), 半 径r =1, 圆 C 的圆心
为C (2, 一2),半径r =1, 且圆C 与圆C 的圆心距d=√2 +(-2)
=22>1+1,即 d>r +r , 故两圆外离.
3.已知圆C :x +y —8x—4y+11=0 和圆C :x +y +2y-3=0, 则两
圆的公切线有( )
A.1 条 B.2 条
C.3 条 D.4 条
解析:圆C 的标准方程为(x-4) +(y-2) =9,则圆心为C (4,2), 半径
r =3;
圆C 的标准方程为x +(y+1) =4, 则圆心为C (0, 一1),半径r =2.
因为两圆的圆心距|C C I= √ (4-0) +(2+1) =5,
所以|C C I=r +r , 即圆心C 和圆C 外切,可知两圆有3条公切线。
故选C.
4.若圆C :(x+1) +(y+1) =4 与圆C :(x—2) +(y-3) =m 内切,则m
●
解析:因为圆C :(x+1) +(y+1) =4, 圆 C :(x—2) +(y—3) =m,
所以圆心距d=√(2+1) +(3+1) =5.
因为圆C 与圆C 内切,所以5=Nm —2|,所以m=49.
答案:49
探究点1 圆与圆位置关系的判断
[问题探究]
根据代数法确定两个圆的位置关系时,能否准确得出两圆的位置关系
提示:不能,如两圆方程组成的方程组有一组解,两圆外切或内切.
已知圆C :x +y —2mx+4y+m —5=0, 圆C :x +y +2x—
2my+m —3=0, 问:m 为何值时,(1)圆C 与圆C 外切 (2)圆C 与圆C 内含
【解】 对于圆C , 圆 C 的方程,
配方得C :(x—m) +(y+2) =9,
C :(x+1) +(y—m) =4.
(1)如果圆C 与圆C 外切,
则有 (m+1) +(-2-m) =3+2,
即m +3m—10=0,
解得m=—5 或 m=2.
故当m=—5 或2时,圆C 与圆C 外切.
(2)如果圆C 与圆C 内含,
则有 √(m+1) +(-2-m) <3-2,
即(m+1) +(m+2) <1, 整理得m +3m+2<0,
解得一2
(1)几何法:将两圆的圆心距d与两圆的半径之差的绝对值、半径之和进
行比较,进而判断出两圆的位置关系,这是在解析几何中主要使用的方
法 .
(2)代数法:将两圆的方程组成方程组,通过解方程组,根据方程组解的
个数进而判断两圆位置关系.
= 判断下列两圆的位置关系:
(1)(x+2) +(y—2) =1 与(x—2) +(y-5) =16; (2)x +y +6x—7=0 与x +y +6y—27=0.
解:(1)根据题意,得两圆的半径分别为r =1 和 r =4,
两圆的圆心距d=√ [2-(-2)] +(5-2) =5.
因为d=r +r , 所以两圆外切.
(2)将两圆的方程化为标准方程,得(x+3) +y =16,x +(y+3) =36.
故两圆的半径分别为R=4 和r=6,
因为IR—r
例2已知圆C 与圆C :x +y —2x=0 相外切,并且与直线x+ √3 y=0
相切于点A(3,一 √3),求圆C 的方程.
【解】 设圆C 的方程为(x—a) +(y—b) =r (r>0),
因为圆C 与圆C :(x—1) +y =1 相外切,
所以 √b +(a-1) =r+1.①
又因为圆C 与直线x+ √3 y=0相切于A(3, 一 √3),
由①②③解 或
故圆C 的方程为(x—4) +y =4或x +( y+43 ) =36.
1. 若圆x +y =m 与圆x +y +6x—8y—11=0 内切,则m=
解析:圆 x +y =m 的圆心坐标为(0,0),半径 ,
圆x +y +6x—8y—11=0 的圆心坐标为(一3,4),半径 r =6.
因为两圆内切,且圆心距d=5, 所以|6- √m |=5,
解得m=1 或 m=121.
答案:1或121
2.求与圆C:(x—2) +(y+1) =4 相切于点A(4,一1)且半径为1的圆的方
程.
解:已知圆C:(x—2) +(y+1) =4 的圆心为C(2, 一 1).
设所求圆B 的圆心为B(a,b), 切点为A(4,一 1),则点C,A,B 共线.
则b=—1,
又因为 A|B|=1, 可得a=5 或3,
即圆心B 的坐标为(5,一1)或(3,一1),
故圆B的方程为(x—5) +(y+1) =1 或(x—3) +(y+1) =1.
探究点3 与两圆相交有关的问题
已知圆C :x +y +2x—6y+1=0, 圆C :x +y —4x+2y-11=
0,求两圆的公共弦所在的直线方程及公共弦长.
① 一 ②,得3x—4y+6=0.
因为A,B 两点坐标都满足此方程,
所以3x—4y+6=0 即为两圆公共弦所在直线的方程。
易知圆C 的圆心为C (一1,3),半径r=3.
【 解】 设两圆交点为 A,B, 则 A,B 两点的坐标均满足方程组
即两圆的公共弦长
又点C 到直线AB 的距离
●
(1)两圆相交时,公共弦所在的直线方程
若圆C :x +y +D x+E y+F =0 与圆C :x +y +D x+E y+F =0 相
交,则两圆公共弦所在直线的方程为(D -D )x+ (E 一E )y+F -F =0.
(2)圆系方程
一般地过圆C :x +y +D x+E y+F =0 与圆C :x +y +D x+E y+
F =0 交点的圆的方程可设为:x +y +D x+E y+F +λ(x +y +D x+ E y+F )=0(λ≠ 一1),然后再根据其他条件求出λ,即可得圆的方程.
== 求经过两圆x +y +6x—4=0 和x +y +6y—28=0 的交点
且圆心在直线x—y-4=0 上的圆的方程.
解:方法一:解方程
得两圆的交点A(—1,3),B(—6,—2).
设所求圆的圆心为(a,b), 因为圆心在直线x—y-4=0 上,故b=a—4.
解得
故圆心 9
半径为
故圆的方程
即x +y —x+7y—32=0.
方法二:因为圆x +y +6y—28=0 的圆心(0,—3)不在直线x—y—4=0
上,故可设所求圆的方程为x +y +6x—4+λ(x +y +6y—28)=0(λ≠
—1),其圆心 代入x—y-4=0, 求得λ=—7.
故所求圆的方程为x +y —x+7y—32=0.
1. 圆O :x +y -4y+3=0 与圆O :x +y —16y=0 的位置关系是( )
A. 相离 B. 相交
C. 相 切 D . 内含
解析:因 为O (0,2),r =1,O (0,8),r =8,|O O I=
(0 — 0) +(2 - 8) =6,则 |O O I
A.(1,0) 和(0,1) B.(1,0) 和(0,—1)
C. (一1,0)和(0,一1) D. (一1,0)和(0,1)
解
所以两圆的交点坐标为(—1,0)和(0,—1).
解析:
3.已知圆C :(x—2) +(y-1) =10 与圆C :(x+6) +(y+3) =50 交于
A,B 两点,则AB所在的直线方程是
解析:两圆方程相减可得一16x—32—8y— 8=—40,整理得2x+ y=0.
答案:2x+y=0
4. 已知以C(3,4) 为圆心的圆与圆x +y =1 外切,求圆C的方程。
解:设圆C 的半径为r, 则 圆C 的方程为(x—3) +(y-4) =r .
由题意得两圆圆心距d= √ (3-0) +(4-0) =5,
因为两圆外切,所以圆心距等于两圆半径之和,即5=r+1, 解得r=4.
故圆C 的方程为(x—3) +(y—4) =16.
应用案▼巩固提升
[ 强 化 培 优 通关]
[A 基础达标]
1. 两圆x +y —1=0 和x +y —4x+2y—4=0 的位置关系是( )
A. 内切 B. 相交
C. 外 切 D. 外 离
解析:将两圆化成标准方程分别为x +y =1,(x—2) +(y+1) =9, 可知圆
心距d=√5, 由于2
程是x—y+1=0, 则( )
A.E=—4,F=8 B.E=4,F=—8
C.E=—4,F=—8 D.E=4,F=8
得4x+Ey-4—F=0, 则 9
解得E=—4,F=— 8, 故选C.
解析:由题意联立两圆方程
。
3 . 已知圆 x +y —4x+6y=0 和圆x +y —6x=0 交于A,B 两点,则公共
弦AB 的垂直平分线的方程为( )
A.x+y+3=0 B.2x—y—5=0
C.3x—y-9=0 D.4x—3y+7=0
解析:由题意知公共弦AB 的垂直平分线即为两圆圆心连线所在的直线.
两圆的圆心分别为(2,—3),(3,0),
所以所求直线的斜率 故直线方程为3x—y—9=0.
4.已知圆M:(x—a) +y =4(a>0) 与圆N:x +(y—1) =1 外切,则直线x
-y- √2 =0被圆M 截得的线段的长度为( )
A.1 B.√
C.2
解析:由题意,知√a +1 =2+1,a>0,
所以 a=2√2, 圆心 M(22,0) 到直线 x—y-√2=0 的距离 d=
所以直线x-y- √2=0 被圆M 截得的线段的长度为2/4-1 =2\3,故
选D.
5.(多选)已知半径为1的动圆与圆(x—5) +(y+7) =16相切,则动圆圆心
的轨迹方程是( )
A.(x—5) +(y—7) =25
B.(x—5) +(y—7) =17
C/(x—5) +(y+7) =9
D/(x-5) +(y+7) =25
解析:设动圆圆心为(x,y),若动圆与已知圆外切,则√(x-5) +(y+7)
=4+1,
所 以(x —5) +(y+7) =25; 若 动 圆 与 已 知 圆 内 切 , 则
所以(x—5) +(y+7) =9.
6. 若圆x +y —2ax+a =2 和x +y —2by+b =1 外离,则a,b 满足的条
件是 ●
解析:由题意可得两圆圆心坐标和半径长分别为(a,0),√2 和(0,b),1,
因为两圆相离,所以 √a +b >12 +1,
即a +b >3+2 √2.
答案:a +b >3+2 √2
7. 若点A(a,b) 在圆x +y =4 上,则圆(x—a) +y =1 与圆x +(y—b) =1
的位置关系是 ●
解析:因为点A(a,b)在圆x +y =4 上,所以a +b =4.
又圆x +(y—b) =1 的圆心C (0,b), 半径 r =1,
圆(x—a) +y =1的圆心C (a,0),半径r =1,
则圆心距d=|C C I=√a +b =√4 =2=r +r ,
所以两圆外切.
答案:外切
8. 以(3,—4)为圆心,且与圆x +y =64 内切的圆的方程是
解析:圆x +y =64 的圆心为(0,0),半径r =8,
所以圆心距 d=√3 +4 =5,
设所求圆半径为r,则 |r—r'=d,
所以|r—8|=5,
所以r=3 或r=13.
所以圆的方程为(x—3) +(y+4) =9或(x—3) +(y+4) =169.
答案:(x—3) +(y+4) =9或(x—3) +(y+4) =169
9.已知圆C :x +y —2mx+4y+m —5=0 与圆C :x +y +2x=0.
(1)当m=1 时,判断圆C 与圆C 的位置关系;
(2)是否存在m 使得圆C 与圆C 内含
解:(1)因为m=1, 所以两圆的方程分别可化为C :(x—1) +(y+2) =9,
C :(x+1) +y =1.
又因为r +r =3+1=4,r —r =3—1=2,
所以圆C 与圆C 相交.
所以r —r
则 √(m+1) +(-2-0) <3-1,
即(m+1) <0, 显然该不等式无解.
故不存在m 使得圆C 与圆C 内含.
10.(2021·吉林省高一期末)已知圆M:x +y —2ay=0(a>0)截直线x+y=0
所得线段的长度是2 √2,判断圆M 与圆N:(x—1) +(y—1) =1的位置关 系。
解:把圆M 的方程化为标准方程为x +(y—a) =a ,
所以M(0,a),r =a.
所以点M 到直线x+y=0 的距离
由题意可得, +2=a , 所 以a=2,
所以M(0,2),r =2. 又N(1,1),r =1,
所以|MN|=√2, 所以|r —r k|MN
[B 能力提升]
11.已知点M 在圆C :(x+3) +(y—1) =4 上,点N 在圆C :(x—1) +(y
十2) =4上,则|MNI的最大值是( )
A.5 B.7
C.9 D.11
解析:由题意知圆C 的圆心C (一3,1),半径长r =2; 圆 C 的圆心C (1,
—2),半径长r =2.
因为两圆的圆心距
所以两圆相离,从而|MNI 的最大值为d +r +r =5+2+2= 9.故选C.
12.过圆 x +y —x—y—2=0与圆x +y +4x—4y—8=0 的交点和点(3,1)
的圆的方程是 ●
解析:设所求圆方程为 x +y —x—y—2+λ(x +y +4x—4y—8)=0,将(3,
1)代入得 .故所求圆的方程为
答案:
13.若⊙0: x +y =5 与⊙O :(x—m) +y =20(m∈R) 相交于A,B 两点
且两圆在点A 处的切线互相垂直,则线段AB的长度为 ●
解析:如图所示,在Rt△00 A 中 ,OA=√5,O A=2√ ,
所以AB=4.
答案:4
所以00 =5,
14. 已知圆O 的方程为x +(y+1) =4, 圆 O 的圆心为O (2,1).
(1)若圆O 与圆O 外切,求圆O 方程;
(2)若圆O 与圆O 交于A,B 两点,且AB|=2 √2, 求圆O 的方程.
解:(1)设圆O 、圆O 的半径分别为r ,r , 则r =2.
因为两圆外切,所以|O O I=r +r ,
所以圆O 的方程是(x—2) +(y-1) =12-82.
圆 O ,O 的方程相减,即得两圆公共弦AB 所在直线的方程,为4x+4y+
r3-8=0.
所以圆心 O (0, 一1)到直线AB 的距离
√ 2,解得r =4 或r3=20.
所以圆O 的方程为(x—2) +(y-1) =4 或(x—2) +(y—1) =20.
[C 拓展探究]
15. 已知动点P 到两个定点0(0,0),A(3,0) 的距离的比为 ●
(1)求动点P 的轨迹C 的方程;
(2)已知圆Q 的圆心为 Q(t,t)(t>0),且圆Q 与 x 轴相切,若圆 Q 与曲线C
有公共点,求实数t 的取值范围.
解:(1)设P(x,y), 则 |AP|=2|OP|,
即|APl =4|OPP ,
所以(x—3) +y =4(x +y ),
整理得(x+1) +y =4.
所以动点P 的轨迹C 的方程为(x+1) +y =4.
(2)因为点Q 的坐标为(t,t)(t>0),且 圆Q 与x 轴相切,所以圆Q 的半径为t,
所以,圆Q 的方程为(x—t) +(y—t) =t.
因为圆Q 与圆C 有公共点,
又圆Q 与圆C 的圆心距为
所以|2—t|≤|CQI≤2+t,
即(2—t) ≤2t +2t+1≤(2+t) ,
解得 — 3+23 ≤t≤3.
所以,实数t的取值范围是[-3+2\3,3].
