3.1.2 椭圆的简单几何性质(第1课时) 课件(共30张PPT)-高中数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 3.1.2 椭圆的简单几何性质(第1课时) 课件(共30张PPT)-高中数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 00:00:00 | ||
图片预览









文档简介
(共30张PPT)
第三章圆锥曲线的方程
3.1.2 椭圆的简单几何性质(第1课时)
人教A 版2019选修第一册
学习目标
1.根据椭圆的方程研究椭圆的几何性质.
2.了解离心率对椭圆扁平程度的影响,培养数学运算的核心素养.
3.根据几何条件求出椭圆的方程.
4.掌握椭圆标准方程中的a,b 以及c,e 的几何意义,a,b,c,e 之间的相互关系。
01导入
P A R T 0 N E
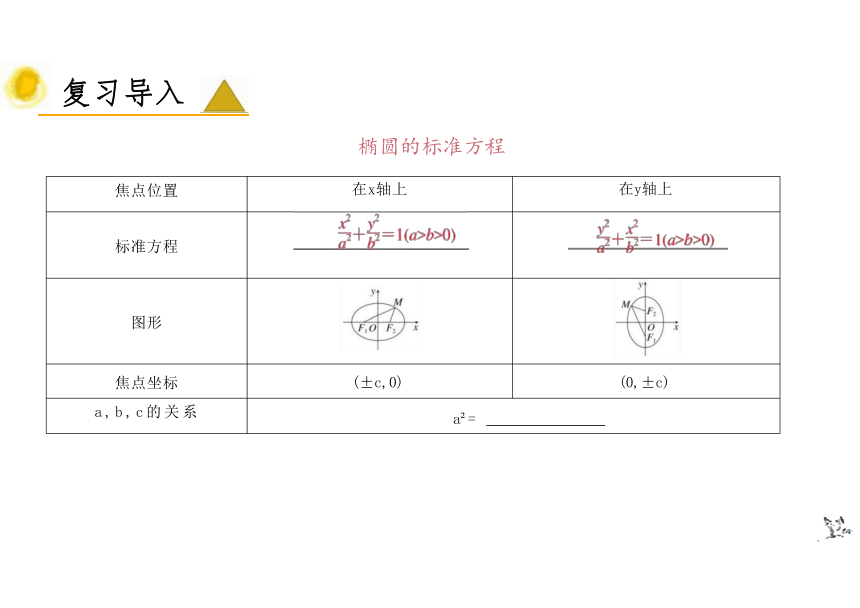
焦点位置 在x轴上
在y轴上
标准方程
图形
焦点坐标 (±c,0)
(0,±c)
a,b,c的关系 a =
复习导入
椭圆的标准方程
与利用直线的方程、圆的方程研究它们的几何性质一样,我们利用椭圆的标
准方程研究椭圆的几何性质,包括椭圆的范围、形 状、大小、对称性和特殊点 等.
复习导入
来研究椭圆的几何性质.
下面,我们用椭圆方程
02椭圆的简单的几何性质
P A R T 0 N E
范围吗 它具有怎样的对称性 椭圆上哪些点比较特殊
y 个
B
A
F o F
B
椭圆的简单几何性质
的形状,你能从图上看出它的
探究: 观察椭圆
A
2
x
程(代数法)确定出它的具体边界吗
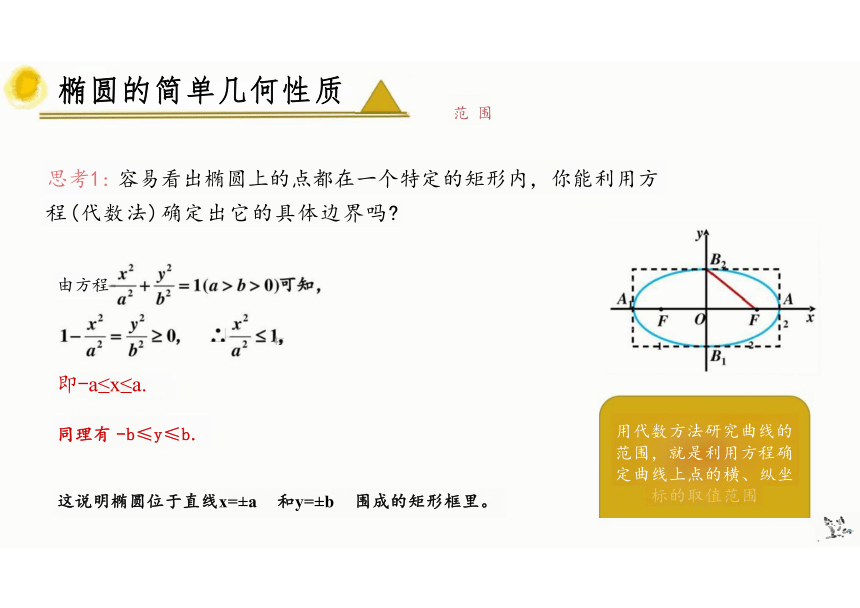
由方程
即-a≤x≤a.
同理有 -b≤y≤b.
这说明椭圆位于直线x=±a 和y=±b 围成的矩形框里。
用代数方法研究曲线的 范围,就是利用方程确 定曲线上点的横、纵坐
标的取值范围
椭圆的简单几何性质
思考1: 容易看出椭圆上的点都在一个特定的矩形内,你能利用方
范 围
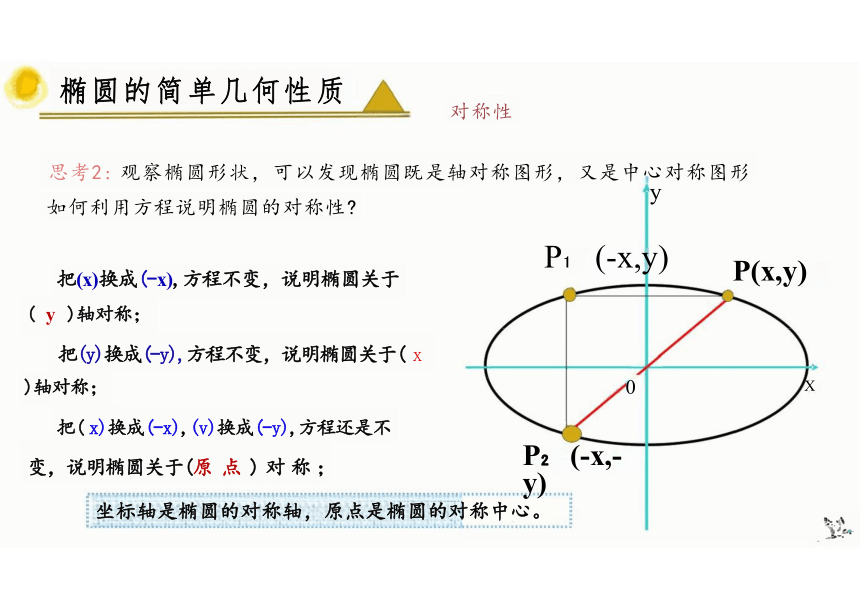
如何利用方程说明椭圆的对称性
把(x)换成(-x),方程不变,说明椭圆关于
( y )轴对称;
把(y)换成(-y),方程不变,说明椭圆关于( x
)轴对称;
把( x)换成(-x),(v)换成(-y),方程还是不
变,说明椭圆关于(原 点 ) 对 称 ;
椭圆的简单几何性质
思考2: 观察椭圆形状,可以发现椭圆既是轴对称图形,又是中心对称图形
0
P (-x,-y)
y
P (-x,y)
坐标轴是椭圆的对称轴,原点是椭圆的对称中心。
P(x,y)
对称性
X
椭圆与坐标轴有四个交点,这四个点比较特殊.
在椭圆方程 (a>b>0) 中,令x=0, 得y=±b,
说明椭圆与y轴有两个交点,坐标分别为
令y=0,得x=±a, 说明椭圆与x轴有两个交点,坐标分别为 A (-a,0),A (a,0).
所以椭圆与它的对称轴有四个交点,这四个交点叫做椭圆的顶点.
所以椭圆与它的对称轴有四个交点,这四个交点叫做椭圆的顶点.
线段A A ,B B 分别叫做椭圆的长轴和短轴,它们的长分别等于2a,2b. a和b分别叫做椭圆的长半轴长和短半轴长.
椭圆的简单几何性质
思考3:你认为椭圆上哪些点比较特殊 为什么 如何得到这些点的坐标
顶点
如右图示,椭圆 0的长半轴长为a, 半
焦距为c.利用信息技术发现,保持长半轴长a不变,改变椭圆
的半焦距c, 可以发现,c 越接近a, 椭圆越扁平.类似地,保持c 不变,改变a的大小,则a越接近c,椭圆越扁平;而当a,c扩大或
缩小相同倍数时,椭圆的形状不变.这样,利用c和a这两个量,
可以刻画椭圆的扁平程度.
思考4: 观察图形,我们发现,不同椭圆的扁平程度不同.扁平程度是椭
圆的重要形状特征,你能用适当的量定量刻画椭圆的扁平程度吗
椭圆的简单几何性质
c=1.2
a=1.81
66
a=1.81
G=0.83
5
0.
离心率
yA
o
x
椭圆的简单几何性质
我们]把椭圆的焦距与长轴长的比 称为椭圆的离心率,用e表示,即
说明:
(1)离心率的取值范围:因为a>c>0, 所以0(2)离心率对椭圆形状的影响:
①e 越接近1,c 就越接近a, 从而b就越小,椭圆就越扁;
②e 越接近0,c 就越接近0,从而b就越大,椭圆就越圆; ③离心率越小,椭圆越圆,离心率越大,椭圆越扁。
④特例:e =0, 则a =b, 则c =0, 两个焦点重合,椭圆变成圆.
离心率
焦点的位置 焦点在x轴上
焦点在y轴上
图形
标准方程
范围 x|≤a,|yl≤b
x|≤b,|yl≤a
顶点 (±a,0),(0,±b)
(±b,0),(0,±a)
轴长 短 轴 长 =2h , 长 轴 长 =2a
焦点 (±c,0)
(0,±c)
焦距 2c
对称性 对 称 轴 :x轴、y轴, 对称中心:(0,0)
离心率
椭圆的简单几何性质
椭圆的简单几何性质
03性质应用
P A R T 0 N
于是a=5,b=4,c= √25-16=3.
因此,椭圆的长轴和短轴的长分别是2a=10, 和2b=8,离心率
两个焦点坐标分别是F (-3,0)和F (3,0),
四个顶点坐标分别是A (-5,0),A (5,0),B (0,-4),B (0,4).
椭圆的简单几何性质
例1求椭圆16x +25y =400的长轴和短轴的长、离心率、焦点和顶点的坐标。
把原方程化成标准方程,得
椭圆的简单几何性质
练习:已知椭圆C: 设椭圆C 与椭圆C 的长轴长、
短轴长分别相等,且椭圆C 的焦点在y 轴上.
(1)求椭圆C 的长半轴长、短半轴长、焦点坐标及离心率;
(2)写出椭圆C 的方程,并研究其性质.
解:(1)由椭圆C : 得其长半轴长为10,短半
轴长为8,焦点坐标(6,0),(一6,0),离心率
(2)椭圆C :
性质:①范围: —8≤x≤8,—10≤y≤10;
②对称性:关于x 轴、y 轴、原点对称;
③顶点:长轴端点(0,10),(0,—10),短轴端点(一8,0),(8,0);
④离心率:
椭圆的简单几何性质
例 2 根据下列条件,求中心在原点,对称轴在坐标轴上的椭圆方程。
(1)焦点在x 轴上, 一个焦点与短轴的两端点连线互相垂直,且半焦距为6;
(2)与椭l 有相同的焦点,且离心率
(3)以直线3x+4y—12 =0 与两坐标轴的交点为一个顶点和一个焦点.
椭圆的简单几何性质
解 : (1)依题意有 ∴b=c=6,∴a =b +c =72.
∴所求的椭圆方程为
(2)∵c=√9-4=√5,
∴所求椭圆的焦点为(- √ 5,0),( √ 5,0).
设所求椭圆的方程
,c=√5, ∴a=5,b =a —c =20. ∴所求椭圆的方程为
·
·
椭圆的简单几何性质
椭圆的简单几何性质
方法总结
利用性质求椭圆的标准方程的方法:
(1)确定标准方程的形式.
(2)由a,b,c,e 的关系列出方程.
(3)利用待定系数法求出椭圆方程,焦点不明确时要分类讨论.
练习:求适合下列条件的椭圆的标准方程.
(1)长轴长是短轴长的5倍,且过点A(5,0).
(2)离心率 焦距为12.
解:(1)若椭圆焦点在x 轴上,设其标准方程为
由题意得
椭圆的简单几何性质
解得
故所求椭圆的标准方程
若焦点在y 轴上,设其标准方程
故所求椭圆的标准方程
综上所述,所求椭圆的标准方程
椭圆的简单几何性质
由题意,得
解
(2)由 ,2c=12, 得 a=10,c=6,
则b =a —c =64.
当焦点在x 轴上时,所求椭圆的标准方程为
当焦点在y 轴上时,所求椭圆的标准方程为
综上所述,所求椭圆的标准方程为
椭圆的简单几何性质
例3.已知F ,F 是椭圆的两个焦点,过F 且与椭圆长轴垂直的直线交椭圆于A,B 两点,若
△ABF 是正三角形,求该椭圆的离心率.
解:不妨设椭圆的焦点在x轴上,因为ABLF F , 且△ABF 为正三角形,
所以在Rt△AF F 中,∠AF F =30°,
令|AF I=x, 则|AF I=2x, 所以|F F I= √ |AF I -|AF I = √3x=2c,
再由椭圆的定义,可知|AF I+|AF I=2a=3x,
所)
椭圆的简单几何性质
椭圆的离心率的求法
求椭圆的离心率,关键是寻找a 与 c 的关系, 一般地:
(1)若已知 a,c, 则直接代入 求解;
(2)若已知a,b, 则 由 求解
(3)若已知a,b,c 的关系,则可转化为a,c 的齐次式,
再转化为含e 的方程求解即可.
椭圆的简单几何性质
练习:直线l 经过椭圆的一个顶点和一个焦点,若椭圆中心(坐标原点)到l 的距离为其短轴
长的 ) 则该椭圆的离心率为( )
A B C 口
解:利用椭圆的几何性质列方程求离心率.
不妨设椭圆方程 直线l 经过椭圆的一个顶点B(0,b) 和
椭圆的简单几何性质
一个焦点F(c,O), 则直线l 的方程 ,即bx+cy-bc=0.
解 , 即 故选B.
由题意知
练习:若椭圆 的离心率 则 k 的值等于
解:分两种情况进行讨论:
当焦点在x 轴 上 时 ,a =k+8,b =9, 得 c =k—1,
又 少 解得k=4.
当焦点在y 轴 上 时 ,a =9,b =k+8, 得 c =1—k,
椭圆的简单几何性质
又 ,∴
∴k=4 或
解得
··
··
:
例 4 已知椭圆方程 右焦点为F(1,0), 求椭圆上的点到F 距离的最值.
解:设P 为椭圆上一点,坐标为(xo,yo). 连 接PF ,
∴|PF I =(xo—1) +yo .
∵P 为椭圆上一点, 即
∴当xo=—2 时, |PF |的最大值为3;
当xo=2 时, |PF l的最小值为1.
椭圆的简单几何性质
,—2≤xo≤2.
··
04课堂小结
P A R T 0 N E
范围
对称性
顶点
离心率
课堂小结
椭圆的几何性质
应用
第三章圆锥曲线的方程
3.1.2 椭圆的简单几何性质(第1课时)
人教A 版2019选修第一册
学习目标
1.根据椭圆的方程研究椭圆的几何性质.
2.了解离心率对椭圆扁平程度的影响,培养数学运算的核心素养.
3.根据几何条件求出椭圆的方程.
4.掌握椭圆标准方程中的a,b 以及c,e 的几何意义,a,b,c,e 之间的相互关系。
01导入
P A R T 0 N E
焦点位置 在x轴上
在y轴上
标准方程
图形
焦点坐标 (±c,0)
(0,±c)
a,b,c的关系 a =
复习导入
椭圆的标准方程
与利用直线的方程、圆的方程研究它们的几何性质一样,我们利用椭圆的标
准方程研究椭圆的几何性质,包括椭圆的范围、形 状、大小、对称性和特殊点 等.
复习导入
来研究椭圆的几何性质.
下面,我们用椭圆方程
02椭圆的简单的几何性质
P A R T 0 N E
范围吗 它具有怎样的对称性 椭圆上哪些点比较特殊
y 个
B
A
F o F
B
椭圆的简单几何性质
的形状,你能从图上看出它的
探究: 观察椭圆
A
2
x
程(代数法)确定出它的具体边界吗
由方程
即-a≤x≤a.
同理有 -b≤y≤b.
这说明椭圆位于直线x=±a 和y=±b 围成的矩形框里。
用代数方法研究曲线的 范围,就是利用方程确 定曲线上点的横、纵坐
标的取值范围
椭圆的简单几何性质
思考1: 容易看出椭圆上的点都在一个特定的矩形内,你能利用方
范 围
如何利用方程说明椭圆的对称性
把(x)换成(-x),方程不变,说明椭圆关于
( y )轴对称;
把(y)换成(-y),方程不变,说明椭圆关于( x
)轴对称;
把( x)换成(-x),(v)换成(-y),方程还是不
变,说明椭圆关于(原 点 ) 对 称 ;
椭圆的简单几何性质
思考2: 观察椭圆形状,可以发现椭圆既是轴对称图形,又是中心对称图形
0
P (-x,-y)
y
P (-x,y)
坐标轴是椭圆的对称轴,原点是椭圆的对称中心。
P(x,y)
对称性
X
椭圆与坐标轴有四个交点,这四个点比较特殊.
在椭圆方程 (a>b>0) 中,令x=0, 得y=±b,
说明椭圆与y轴有两个交点,坐标分别为
令y=0,得x=±a, 说明椭圆与x轴有两个交点,坐标分别为 A (-a,0),A (a,0).
所以椭圆与它的对称轴有四个交点,这四个交点叫做椭圆的顶点.
所以椭圆与它的对称轴有四个交点,这四个交点叫做椭圆的顶点.
线段A A ,B B 分别叫做椭圆的长轴和短轴,它们的长分别等于2a,2b. a和b分别叫做椭圆的长半轴长和短半轴长.
椭圆的简单几何性质
思考3:你认为椭圆上哪些点比较特殊 为什么 如何得到这些点的坐标
顶点
如右图示,椭圆 0的长半轴长为a, 半
焦距为c.利用信息技术发现,保持长半轴长a不变,改变椭圆
的半焦距c, 可以发现,c 越接近a, 椭圆越扁平.类似地,保持c 不变,改变a的大小,则a越接近c,椭圆越扁平;而当a,c扩大或
缩小相同倍数时,椭圆的形状不变.这样,利用c和a这两个量,
可以刻画椭圆的扁平程度.
思考4: 观察图形,我们发现,不同椭圆的扁平程度不同.扁平程度是椭
圆的重要形状特征,你能用适当的量定量刻画椭圆的扁平程度吗
椭圆的简单几何性质
c=1.2
a=1.81
66
a=1.81
G=0.83
5
0.
离心率
yA
o
x
椭圆的简单几何性质
我们]把椭圆的焦距与长轴长的比 称为椭圆的离心率,用e表示,即
说明:
(1)离心率的取值范围:因为a>c>0, 所以0
①e 越接近1,c 就越接近a, 从而b就越小,椭圆就越扁;
②e 越接近0,c 就越接近0,从而b就越大,椭圆就越圆; ③离心率越小,椭圆越圆,离心率越大,椭圆越扁。
④特例:e =0, 则a =b, 则c =0, 两个焦点重合,椭圆变成圆.
离心率
焦点的位置 焦点在x轴上
焦点在y轴上
图形
标准方程
范围 x|≤a,|yl≤b
x|≤b,|yl≤a
顶点 (±a,0),(0,±b)
(±b,0),(0,±a)
轴长 短 轴 长 =2h , 长 轴 长 =2a
焦点 (±c,0)
(0,±c)
焦距 2c
对称性 对 称 轴 :x轴、y轴, 对称中心:(0,0)
离心率
椭圆的简单几何性质
椭圆的简单几何性质
03性质应用
P A R T 0 N
于是a=5,b=4,c= √25-16=3.
因此,椭圆的长轴和短轴的长分别是2a=10, 和2b=8,离心率
两个焦点坐标分别是F (-3,0)和F (3,0),
四个顶点坐标分别是A (-5,0),A (5,0),B (0,-4),B (0,4).
椭圆的简单几何性质
例1求椭圆16x +25y =400的长轴和短轴的长、离心率、焦点和顶点的坐标。
把原方程化成标准方程,得
椭圆的简单几何性质
练习:已知椭圆C: 设椭圆C 与椭圆C 的长轴长、
短轴长分别相等,且椭圆C 的焦点在y 轴上.
(1)求椭圆C 的长半轴长、短半轴长、焦点坐标及离心率;
(2)写出椭圆C 的方程,并研究其性质.
解:(1)由椭圆C : 得其长半轴长为10,短半
轴长为8,焦点坐标(6,0),(一6,0),离心率
(2)椭圆C :
性质:①范围: —8≤x≤8,—10≤y≤10;
②对称性:关于x 轴、y 轴、原点对称;
③顶点:长轴端点(0,10),(0,—10),短轴端点(一8,0),(8,0);
④离心率:
椭圆的简单几何性质
例 2 根据下列条件,求中心在原点,对称轴在坐标轴上的椭圆方程。
(1)焦点在x 轴上, 一个焦点与短轴的两端点连线互相垂直,且半焦距为6;
(2)与椭l 有相同的焦点,且离心率
(3)以直线3x+4y—12 =0 与两坐标轴的交点为一个顶点和一个焦点.
椭圆的简单几何性质
解 : (1)依题意有 ∴b=c=6,∴a =b +c =72.
∴所求的椭圆方程为
(2)∵c=√9-4=√5,
∴所求椭圆的焦点为(- √ 5,0),( √ 5,0).
设所求椭圆的方程
,c=√5, ∴a=5,b =a —c =20. ∴所求椭圆的方程为
·
·
椭圆的简单几何性质
椭圆的简单几何性质
方法总结
利用性质求椭圆的标准方程的方法:
(1)确定标准方程的形式.
(2)由a,b,c,e 的关系列出方程.
(3)利用待定系数法求出椭圆方程,焦点不明确时要分类讨论.
练习:求适合下列条件的椭圆的标准方程.
(1)长轴长是短轴长的5倍,且过点A(5,0).
(2)离心率 焦距为12.
解:(1)若椭圆焦点在x 轴上,设其标准方程为
由题意得
椭圆的简单几何性质
解得
故所求椭圆的标准方程
若焦点在y 轴上,设其标准方程
故所求椭圆的标准方程
综上所述,所求椭圆的标准方程
椭圆的简单几何性质
由题意,得
解
(2)由 ,2c=12, 得 a=10,c=6,
则b =a —c =64.
当焦点在x 轴上时,所求椭圆的标准方程为
当焦点在y 轴上时,所求椭圆的标准方程为
综上所述,所求椭圆的标准方程为
椭圆的简单几何性质
例3.已知F ,F 是椭圆的两个焦点,过F 且与椭圆长轴垂直的直线交椭圆于A,B 两点,若
△ABF 是正三角形,求该椭圆的离心率.
解:不妨设椭圆的焦点在x轴上,因为ABLF F , 且△ABF 为正三角形,
所以在Rt△AF F 中,∠AF F =30°,
令|AF I=x, 则|AF I=2x, 所以|F F I= √ |AF I -|AF I = √3x=2c,
再由椭圆的定义,可知|AF I+|AF I=2a=3x,
所)
椭圆的简单几何性质
椭圆的离心率的求法
求椭圆的离心率,关键是寻找a 与 c 的关系, 一般地:
(1)若已知 a,c, 则直接代入 求解;
(2)若已知a,b, 则 由 求解
(3)若已知a,b,c 的关系,则可转化为a,c 的齐次式,
再转化为含e 的方程求解即可.
椭圆的简单几何性质
练习:直线l 经过椭圆的一个顶点和一个焦点,若椭圆中心(坐标原点)到l 的距离为其短轴
长的 ) 则该椭圆的离心率为( )
A B C 口
解:利用椭圆的几何性质列方程求离心率.
不妨设椭圆方程 直线l 经过椭圆的一个顶点B(0,b) 和
椭圆的简单几何性质
一个焦点F(c,O), 则直线l 的方程 ,即bx+cy-bc=0.
解 , 即 故选B.
由题意知
练习:若椭圆 的离心率 则 k 的值等于
解:分两种情况进行讨论:
当焦点在x 轴 上 时 ,a =k+8,b =9, 得 c =k—1,
又 少 解得k=4.
当焦点在y 轴 上 时 ,a =9,b =k+8, 得 c =1—k,
椭圆的简单几何性质
又 ,∴
∴k=4 或
解得
··
··
:
例 4 已知椭圆方程 右焦点为F(1,0), 求椭圆上的点到F 距离的最值.
解:设P 为椭圆上一点,坐标为(xo,yo). 连 接PF ,
∴|PF I =(xo—1) +yo .
∵P 为椭圆上一点, 即
∴当xo=—2 时, |PF |的最大值为3;
当xo=2 时, |PF l的最小值为1.
椭圆的简单几何性质
,—2≤xo≤2.
··
04课堂小结
P A R T 0 N E
范围
对称性
顶点
离心率
课堂小结
椭圆的几何性质
应用
