3.2.2 双曲线的简单几何性质 课件(共31张PPT)—— 高中数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 3.2.2 双曲线的简单几何性质 课件(共31张PPT)—— 高中数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 22:16:13 | ||
图片预览











文档简介
(共31张PPT)
第三章圆锥曲线的方程
3.2.2双曲线的简单几何性质
1.理解双曲线的简单几何性质(范围、对称性、顶点、
渐近线、离心率).
2.能用双曲线的简单性质解决一些简单的问题.
学 习 目 标
由方程 ..,
双曲线上点的坐标(x,y) 都适合不等 ..1,y∈R, 即 x ...a ,y∈R.
所以x,,-a, 或 x..a;y∈R.
这说明双曲线位于直线x=-a 及其左侧和直线x=a 及其右侧的区域.
1.范围
2.对称性
双曲线 0)关于x 轴 、y 轴和原点都是对称的
这时,坐标轴是双曲线的对称轴,原点是双曲线的对称中心.双曲线的 对称中心叫做双曲线的中心。
● ●●●
●●
●●●●
在方 中,令y=0, 得 x=±a, 因此双曲线和x 轴有两
个交点A(-a,0), A (a,0).因为x 轴是双曲线的对称轴,所以双曲线和它的对称轴 有两个交点,它们叫做双曲线的顶点.
令x=0, 得 y =-b , 这个方程没有实数解,说明双曲线和y 轴没有公共点, 但也把B (0,-b),B (0,b) 两点画在y轴上(如图) .
线段A A 叫做双曲线的实轴,它的长等于2a,a 叫做双曲线的实半轴长;线段
B B 叫做双曲线的虚轴,它的长等于2b,b 叫做双曲线的虚半轴长.
3 . 顶点
一般地,双曲 的两支向外延伸时,与两条直线
逐渐接近,这两条直线叫做双曲线的渐近线.实际上,双曲线与它的 渐近线无限接近,但永远不相交.
在双曲线方程 中,如果a=b那么方程变为x -y =a ,
此时双曲线的实轴和虚轴的长都等于2a.这时,四条直线x=±a,y=±a 围成正方 形,渐近线方程为y=±x, 它们互相垂直,并且平分双曲线的实轴和虚轴所成的角 实轴和虚轴等长的双曲线叫做等轴双曲线.
4.渐近线
双曲线的焦距和实轴长的比 ,叫做双曲线的离心率.因为c>a>0
所以双曲线的离心率
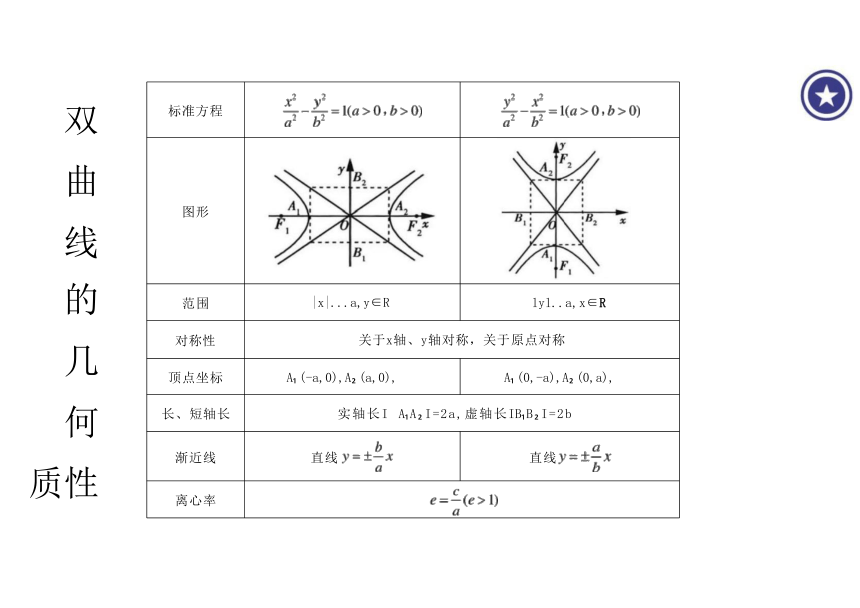
标准方程
图形
范围 |x|...a,y∈R lyl..a,x∈R
对称性 关于x轴、y轴对称,关于原点对称
顶点坐标 A (-a,0),A (a,0), A (0,-a),A (0,a),
长、短轴长 实轴长I A A I=2a,虚轴长IB B I=2b
渐近线 直线 直线
离心率
双 曲 线 的 几 何 性 质
例题巩固
例1求双曲线9y -16x =144 的实半轴长和虚半轴长、焦点坐标、离心率、渐 近线方程.
解:把双曲线的方程9y -1 6x =144化为标准方程
由此可知,实半轴长a=4, 虚半轴长b=3 ;c=√a +b =√4 +3 =5,焦点
坐标是(0,-5) ,(0,5);离心率 ;渐近线方程为
例2双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面如图
它的最小半径为12 m, 上口半径为13 m, 下口半径为25m, 高为55 m.试建立适当 的坐标系,求出此双曲线的方程(精确到1m).
解:根据双曲线的对称性,在冷却塔的轴截面所在平面建立如图所示的
直角坐标系Oxy, 使小圆的直径 AA'在x 轴上,圆心与原点重合.
这时,上、下口的直径CC′,BB '都平行于x 轴,且ICC'|=13×2, |BB' |=25×2.
设双曲线的方程为 ,点C 的坐标为(13,y).
则点B 的坐标为(25,y-55). 因为直径AA'是实轴,所以a=12.
又B,C 两点都在双曲线上,所以
由方程②得 (负值舍去),代入方程①
化简得19b +275b-18150=0③ ,解 得b≈25 (负值舍去) .
因此所求双曲线的方程为
例 3 动 点M(x,y) 与定点F(4,0) l 的距离的比是常
数 ,求动点M 的轨迹.
解:设d 是 点M到直线l 的距离,根据题意,动点M的轨迹就是点的集合
所以点M 的轨迹是焦点在x 轴上,实轴长为6、虚轴长为2√7的双曲线.
将上式两边平方,并化简,得7 即
,由此得
例4如图,过双曲线 的右焦点F , 倾斜角为30°的直线交双曲线于
A,B 两点,求|ABI.
解:由双曲线的标准方程可知,双曲线的焦点分别为F(-3,0), F (3,0).
因为直线AB 的倾斜角是30°,且经过右焦点F ,
所以直线AB的方程为
由 ,消去y得5x +6x-27=0, 解 得x=-3,
将xi,x 的值分别代入①,得y =-2√3,
于是A,B 两点的坐标分别为(-3,-2 √3),
课堂小练
1.已知双曲线
率为(
的一条渐近线方程为
的一条渐近线方程为
则该双曲线的离心率
解析:因为双曲线
则双曲线的离心
.故选A.
所以
B.
C.
口
A
2.若直线l:y=kx+2 与双曲线C:x -y =4 的左、右两支各有一个交点,则实数k
的取值范围是(D
A.(-√2,-1) B.(1,√2) C.(-√2,√2) D.(-1,1)
解析:当 直 线l:y=kx+2 与双曲线C:x -y =4 的渐近线y=±x 平行时,k=±1,
此时直线与双曲线的左支或右支只有一个交点,∵直线l:y=kx+2 与双曲
C:x -y =4 的左、右两支各有一个交点,∴k 的取值范围为(-1,1),故选D.
3.已知双曲线 的一条渐近线平行于直线l:y=2x+10, 双 曲 线
的一个焦点在直线1上,则双曲线的标准方程为
标为(-5,0),∴c=5,∵
l:y=2x+10,∴
.故选A.
解析:∵双曲线的一个焦点在直线1上,当y=0 时 ,x=-5, 即双曲线的左焦点坐
又c =a +b ,∴a = 5,b =20,∴ 双曲线的标准方程为
的一条渐近线平行于直线
双曲线
事
与T 交于C,D 两点,四边形ABCD的两条对角线交于点E,∠AEB=60°, 则双曲
线T 的离心率为((A
,直线y=-b 与 T 交于A,B 两点,直线y=7b
4.已知双曲线T:
D.4
C.2
A
D
B.
的交点E 在y 轴上,易知直线AC的方程为 令x=0, 得
即 因为∠AEB=60°, 所以△ABE是等边三角形, 所
以 ,27a =8b 因为c =a +b , 所以35a =8c , 所 以
解析;在 中,令y=-b, 得 x=± √2a,不 妨 设A( √2a,-b),B(- √2a,-b),
同理可得C(-5 √2a,7b),D(5 √2a,7b),由对称性可知,四边形ABCD 的两条对角线
故选A.
B.离心率
D. 渐近线方程为y=± √3x
半径作圆A, 圆 A 与双曲线C 的一条渐近线交于M,N 两点,若∠MAN=60°, 则
右顶点为A, 以 A 为圆心, b 为
5 . (多选)已知双曲线C:
A.渐近线方程为
C. 离心率
为等边三角形,则A(a,0)到渐近线 的距离为 所以 即
故双曲线的离心率 可得 ,故渐 近线方程为 .故选AC.
解析;由已知,可令M,N 所在的渐近线方程为 由∠MAN=60° 知△MAN
6.若双曲线3x -y =m 的虚轴长为2,则实数m 的值为_- 3 或 1
解析:因为双曲线3x -y =m 的虚轴长为2,①当m>0 时,双曲线方程可化为
则 √m=1, 得m=1;②当 m<0 时,双曲线方程可化为
得m=-3. 故实数 m 的值为-3或1.
则
解析:由题意得,双曲线的渐近线方程为 因此F(c,0) 到一条渐近线的距
离 ,化简得b =3a , 因 此 ,c =4a , 即 c=2a, 从 而
7.若双曲线 的右焦点F(c,0) 到一条渐近线的距离为 则
其离心率的值是 事
解析;不妨设P 为双曲线左支上的一点,由题意,设PF =m,PF =n, 则有m-n=2a
,m +n =4c , , 可得m +n -2mn=4a , 即4c -32=4a
所以20a -32=4a , 即a =2, 则 a= √2.
8.设双曲线 的左、右焦点分别为F,F , 离心率为 √ 5,P 是
双曲线上一点,且FP⊥F P, 若△PFF 的面积为8,则a=
9.回答下列问题:
(1)求焦点在x 轴上,实轴长为4,焦距为8的双曲线的标准方程;
(2)求一个焦点为(5,0),渐近线方程为 的双曲线的标准方程.
解析:(1)设双曲线的标准方程为
由题意,得2a=4,2c=8, 则a=2,c=4, 所 以b=2√3,
所以双曲线的标准方程为
(2)因为双曲线焦点在x 轴上,
所以可设双曲线的标准方程为
所以
解得a =9, 所以b =16,
所以双曲线的渐近线方程为
又焦点为(5,0),所以
所以双曲线的标准方程为
10.已知双曲线C: 的右焦点为F(2,0), 点 F 到 C 的渐近线的
距离为1 .
( 1 ) 求C 的方程.
(2)若直线l 与 C 的右支相切,切点为P,l 与直线l 交于点Q, 问 x 轴上是
否存在定点M, 使 得MP⊥MQ 若存在,求出M 点坐标;若不存在,请说明理由.
解析:(1)易知C 的渐近线方程为bx±ay=0,c=2,
所以 F(2,0)到渐近线的距离
所以a =c -b =3,
所以C 的方程为
(2)由题意易知直线 的斜率存在,设其方程为y=kx+m, 联立互与C 的方程,消去y 得(3k -1)x +6kmx+3m +3=0,
因为直线 与 C 的右支相切,所以
△=36k m -12(3k -1)(m +1)=12(m +1-3k )=0,
得m =3k -1, 则m≠0.
101111101
101111410
11
111111 41111
14 1104110
设切点P(x,y ), 则 4
设Q(x ,y ),因 为Q 是直线l 与直线l 的交点,所以 事
假设x 轴上存在定点M(x ,0), 使 得MP⊥MQ,
则MP.MQ=(x-x ,y)·(x -xo,y )=(x-x,)(x -x )+y y
故存在x =2, 使得MP·MQ=0, 即 MP⊥MQ,
所以x 轴上存在定点M(2,0), 使 得MP⊥MQ.
垂
要
小结:
回顾一下本节课学习了哪些新知识呢
1.范围
2.对称性 3.顶点
4.渐近线 5.离心率
谢 谢观看
第三章圆锥曲线的方程
3.2.2双曲线的简单几何性质
1.理解双曲线的简单几何性质(范围、对称性、顶点、
渐近线、离心率).
2.能用双曲线的简单性质解决一些简单的问题.
学 习 目 标
由方程 ..,
双曲线上点的坐标(x,y) 都适合不等 ..1,y∈R, 即 x ...a ,y∈R.
所以x,,-a, 或 x..a;y∈R.
这说明双曲线位于直线x=-a 及其左侧和直线x=a 及其右侧的区域.
1.范围
2.对称性
双曲线 0)关于x 轴 、y 轴和原点都是对称的
这时,坐标轴是双曲线的对称轴,原点是双曲线的对称中心.双曲线的 对称中心叫做双曲线的中心。
● ●●●
●●
●●●●
在方 中,令y=0, 得 x=±a, 因此双曲线和x 轴有两
个交点A(-a,0), A (a,0).因为x 轴是双曲线的对称轴,所以双曲线和它的对称轴 有两个交点,它们叫做双曲线的顶点.
令x=0, 得 y =-b , 这个方程没有实数解,说明双曲线和y 轴没有公共点, 但也把B (0,-b),B (0,b) 两点画在y轴上(如图) .
线段A A 叫做双曲线的实轴,它的长等于2a,a 叫做双曲线的实半轴长;线段
B B 叫做双曲线的虚轴,它的长等于2b,b 叫做双曲线的虚半轴长.
3 . 顶点
一般地,双曲 的两支向外延伸时,与两条直线
逐渐接近,这两条直线叫做双曲线的渐近线.实际上,双曲线与它的 渐近线无限接近,但永远不相交.
在双曲线方程 中,如果a=b那么方程变为x -y =a ,
此时双曲线的实轴和虚轴的长都等于2a.这时,四条直线x=±a,y=±a 围成正方 形,渐近线方程为y=±x, 它们互相垂直,并且平分双曲线的实轴和虚轴所成的角 实轴和虚轴等长的双曲线叫做等轴双曲线.
4.渐近线
双曲线的焦距和实轴长的比 ,叫做双曲线的离心率.因为c>a>0
所以双曲线的离心率
标准方程
图形
范围 |x|...a,y∈R lyl..a,x∈R
对称性 关于x轴、y轴对称,关于原点对称
顶点坐标 A (-a,0),A (a,0), A (0,-a),A (0,a),
长、短轴长 实轴长I A A I=2a,虚轴长IB B I=2b
渐近线 直线 直线
离心率
双 曲 线 的 几 何 性 质
例题巩固
例1求双曲线9y -16x =144 的实半轴长和虚半轴长、焦点坐标、离心率、渐 近线方程.
解:把双曲线的方程9y -1 6x =144化为标准方程
由此可知,实半轴长a=4, 虚半轴长b=3 ;c=√a +b =√4 +3 =5,焦点
坐标是(0,-5) ,(0,5);离心率 ;渐近线方程为
例2双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面如图
它的最小半径为12 m, 上口半径为13 m, 下口半径为25m, 高为55 m.试建立适当 的坐标系,求出此双曲线的方程(精确到1m).
解:根据双曲线的对称性,在冷却塔的轴截面所在平面建立如图所示的
直角坐标系Oxy, 使小圆的直径 AA'在x 轴上,圆心与原点重合.
这时,上、下口的直径CC′,BB '都平行于x 轴,且ICC'|=13×2, |BB' |=25×2.
设双曲线的方程为 ,点C 的坐标为(13,y).
则点B 的坐标为(25,y-55). 因为直径AA'是实轴,所以a=12.
又B,C 两点都在双曲线上,所以
由方程②得 (负值舍去),代入方程①
化简得19b +275b-18150=0③ ,解 得b≈25 (负值舍去) .
因此所求双曲线的方程为
例 3 动 点M(x,y) 与定点F(4,0) l 的距离的比是常
数 ,求动点M 的轨迹.
解:设d 是 点M到直线l 的距离,根据题意,动点M的轨迹就是点的集合
所以点M 的轨迹是焦点在x 轴上,实轴长为6、虚轴长为2√7的双曲线.
将上式两边平方,并化简,得7 即
,由此得
例4如图,过双曲线 的右焦点F , 倾斜角为30°的直线交双曲线于
A,B 两点,求|ABI.
解:由双曲线的标准方程可知,双曲线的焦点分别为F(-3,0), F (3,0).
因为直线AB 的倾斜角是30°,且经过右焦点F ,
所以直线AB的方程为
由 ,消去y得5x +6x-27=0, 解 得x=-3,
将xi,x 的值分别代入①,得y =-2√3,
于是A,B 两点的坐标分别为(-3,-2 √3),
课堂小练
1.已知双曲线
率为(
的一条渐近线方程为
的一条渐近线方程为
则该双曲线的离心率
解析:因为双曲线
则双曲线的离心
.故选A.
所以
B.
C.
口
A
2.若直线l:y=kx+2 与双曲线C:x -y =4 的左、右两支各有一个交点,则实数k
的取值范围是(D
A.(-√2,-1) B.(1,√2) C.(-√2,√2) D.(-1,1)
解析:当 直 线l:y=kx+2 与双曲线C:x -y =4 的渐近线y=±x 平行时,k=±1,
此时直线与双曲线的左支或右支只有一个交点,∵直线l:y=kx+2 与双曲
C:x -y =4 的左、右两支各有一个交点,∴k 的取值范围为(-1,1),故选D.
3.已知双曲线 的一条渐近线平行于直线l:y=2x+10, 双 曲 线
的一个焦点在直线1上,则双曲线的标准方程为
标为(-5,0),∴c=5,∵
l:y=2x+10,∴
.故选A.
解析:∵双曲线的一个焦点在直线1上,当y=0 时 ,x=-5, 即双曲线的左焦点坐
又c =a +b ,∴a = 5,b =20,∴ 双曲线的标准方程为
的一条渐近线平行于直线
双曲线
事
与T 交于C,D 两点,四边形ABCD的两条对角线交于点E,∠AEB=60°, 则双曲
线T 的离心率为((A
,直线y=-b 与 T 交于A,B 两点,直线y=7b
4.已知双曲线T:
D.4
C.2
A
D
B.
的交点E 在y 轴上,易知直线AC的方程为 令x=0, 得
即 因为∠AEB=60°, 所以△ABE是等边三角形, 所
以 ,27a =8b 因为c =a +b , 所以35a =8c , 所 以
解析;在 中,令y=-b, 得 x=± √2a,不 妨 设A( √2a,-b),B(- √2a,-b),
同理可得C(-5 √2a,7b),D(5 √2a,7b),由对称性可知,四边形ABCD 的两条对角线
故选A.
B.离心率
D. 渐近线方程为y=± √3x
半径作圆A, 圆 A 与双曲线C 的一条渐近线交于M,N 两点,若∠MAN=60°, 则
右顶点为A, 以 A 为圆心, b 为
5 . (多选)已知双曲线C:
A.渐近线方程为
C. 离心率
为等边三角形,则A(a,0)到渐近线 的距离为 所以 即
故双曲线的离心率 可得 ,故渐 近线方程为 .故选AC.
解析;由已知,可令M,N 所在的渐近线方程为 由∠MAN=60° 知△MAN
6.若双曲线3x -y =m 的虚轴长为2,则实数m 的值为_- 3 或 1
解析:因为双曲线3x -y =m 的虚轴长为2,①当m>0 时,双曲线方程可化为
则 √m=1, 得m=1;②当 m<0 时,双曲线方程可化为
得m=-3. 故实数 m 的值为-3或1.
则
解析:由题意得,双曲线的渐近线方程为 因此F(c,0) 到一条渐近线的距
离 ,化简得b =3a , 因 此 ,c =4a , 即 c=2a, 从 而
7.若双曲线 的右焦点F(c,0) 到一条渐近线的距离为 则
其离心率的值是 事
解析;不妨设P 为双曲线左支上的一点,由题意,设PF =m,PF =n, 则有m-n=2a
,m +n =4c , , 可得m +n -2mn=4a , 即4c -32=4a
所以20a -32=4a , 即a =2, 则 a= √2.
8.设双曲线 的左、右焦点分别为F,F , 离心率为 √ 5,P 是
双曲线上一点,且FP⊥F P, 若△PFF 的面积为8,则a=
9.回答下列问题:
(1)求焦点在x 轴上,实轴长为4,焦距为8的双曲线的标准方程;
(2)求一个焦点为(5,0),渐近线方程为 的双曲线的标准方程.
解析:(1)设双曲线的标准方程为
由题意,得2a=4,2c=8, 则a=2,c=4, 所 以b=2√3,
所以双曲线的标准方程为
(2)因为双曲线焦点在x 轴上,
所以可设双曲线的标准方程为
所以
解得a =9, 所以b =16,
所以双曲线的渐近线方程为
又焦点为(5,0),所以
所以双曲线的标准方程为
10.已知双曲线C: 的右焦点为F(2,0), 点 F 到 C 的渐近线的
距离为1 .
( 1 ) 求C 的方程.
(2)若直线l 与 C 的右支相切,切点为P,l 与直线l 交于点Q, 问 x 轴上是
否存在定点M, 使 得MP⊥MQ 若存在,求出M 点坐标;若不存在,请说明理由.
解析:(1)易知C 的渐近线方程为bx±ay=0,c=2,
所以 F(2,0)到渐近线的距离
所以a =c -b =3,
所以C 的方程为
(2)由题意易知直线 的斜率存在,设其方程为y=kx+m, 联立互与C 的方程,消去y 得(3k -1)x +6kmx+3m +3=0,
因为直线 与 C 的右支相切,所以
△=36k m -12(3k -1)(m +1)=12(m +1-3k )=0,
得m =3k -1, 则m≠0.
101111101
101111410
11
111111 41111
14 1104110
设切点P(x,y ), 则 4
设Q(x ,y ),因 为Q 是直线l 与直线l 的交点,所以 事
假设x 轴上存在定点M(x ,0), 使 得MP⊥MQ,
则MP.MQ=(x-x ,y)·(x -xo,y )=(x-x,)(x -x )+y y
故存在x =2, 使得MP·MQ=0, 即 MP⊥MQ,
所以x 轴上存在定点M(2,0), 使 得MP⊥MQ.
垂
要
小结:
回顾一下本节课学习了哪些新知识呢
1.范围
2.对称性 3.顶点
4.渐近线 5.离心率
谢 谢观看
