3.3.1抛物线及其标准方程-课件(共32张PPT)-高中数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 3.3.1抛物线及其标准方程-课件(共32张PPT)-高中数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 959.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 00:00:00 | ||
图片预览







文档简介
(共32张PPT)
人教A 版2019选修第一册
第三章圆锥曲线的方程
3.3.1 抛物线及其标准方程
学习目标
1.掌握抛物线的定义及焦点、准线的概念.
2.掌握抛物线的标准方程及其推导过程.
3.明确p的几何意义,并能解决简单的求抛物线标准方程问题.
01情景导入
P A R T 0 N E
(1)椭圆的离心率范围为0(2) 双曲线的离心率的范围是e>1 ;
(3)当e=1 时,它的轨迹是什么 抛物线
我们已经学习了圆、椭圆、双曲线三种圆锥曲线,今天我们类比椭圆、 双曲线的研究过程与方法,研究另一类圆锥曲线——抛物线.
情景导入
02抛物线及其标准方程
P A R T 0 N E
抛物线及其标准方程
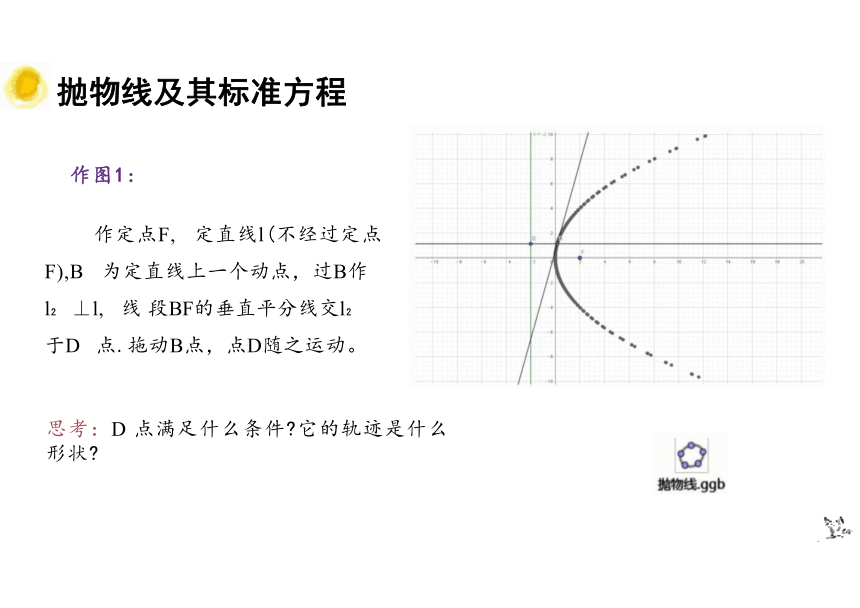
作图1:
作定点F, 定直线l(不经过定点 F),B 为定直线上一个动点,过B作 l ⊥l, 线 段BF的垂直平分线交l 于D 点.拖动B点,点D随之运动。
思考:D 点满足什么条件 它的轨迹是什么 形状
抛物线及其标准方程
思考:D 点满足什么条件 它的轨迹是什么形状
在运动过程中,始终有|BD|=|DF|, 即 点D 与定点F的距离等于它到 定直线的距离,点D的轨迹形状与二次函数的图象相似。
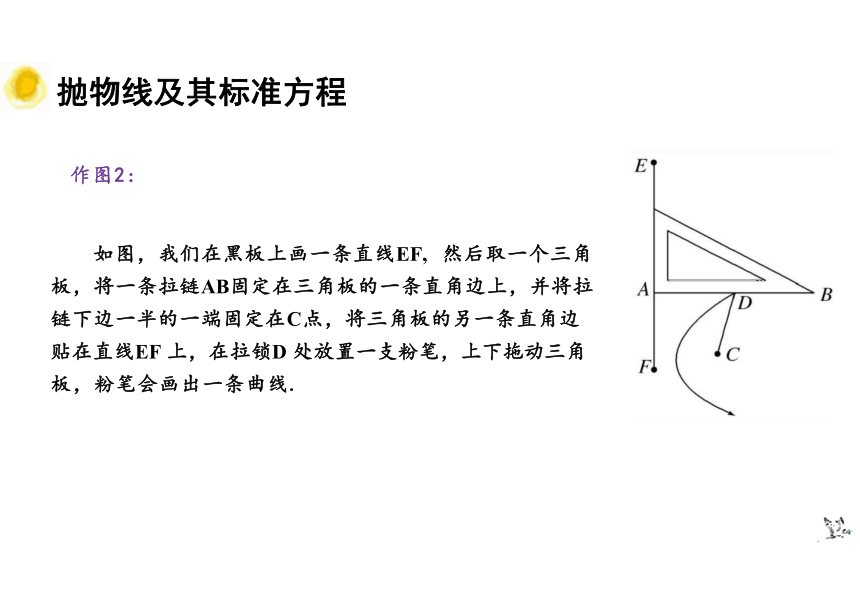
作图2:
如图,我们在黑板上画一条直线EF, 然后取一个三角 板,将一条拉链AB固定在三角板的一条直角边上,并将拉 链下边一半的一端固定在C点,将三角板的另一条直角边 贴在直线EF 上,在拉锁D 处放置一支粉笔,上下拖动三角 板,粉笔会画出一条曲线.
抛物线及其标准方程
抛物线及其标准方程
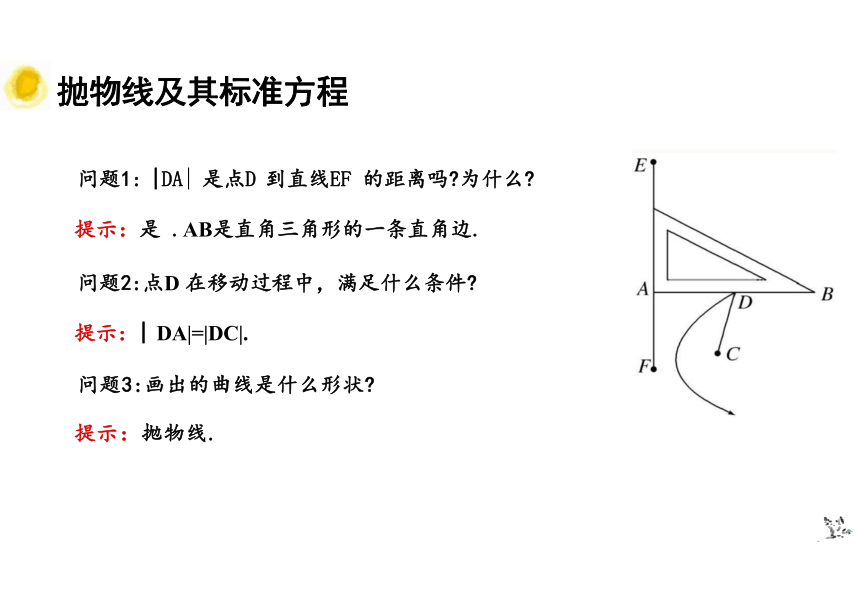
问题1: |DA| 是点D 到直线EF 的距离吗 为什么 提示:是 .AB是直角三角形的一条直角边.
问题2:点D 在移动过程中,满足什么条件 提示:| DA|=|DC|.
问题3:画出的曲线是什么形状
提示:抛物线.
抛物线及其标准方程
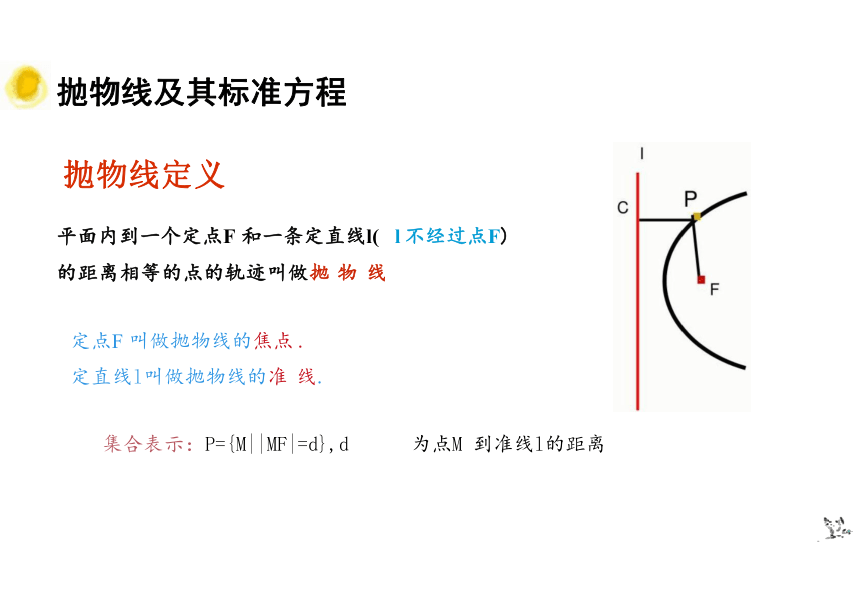
抛物线定义
平面内到一个定点F 和一条定直线l( l 不经过点F) 的距离相等的点的轨迹叫做抛 物 线
定点F 叫做抛物线的焦点 .
定直线l叫做抛物线的准 线.
集合表示:P={M||MF|=d},d 为点M 到准线l的距离
对抛物线定义的认识
(1)定义的实质可归结为“一动三定”;一个动点,设为M; 一个定点F 叫 做抛物线的焦点; 一条定直线l, 叫做抛物线的准线; 一个定值,即点M 与点 F 的距离和它到直线l的距离之比等于1.
(2)注意定点F 不在直线l上,否则动点M 的轨迹不是抛物线,而是过点F 垂直 于直线l的一条直线.
抛物线及其标准方程
抛物线及其标准方程
求轨迹方程
C P_
建立直角坐标系
使方程形式足够简洁 !
设M(x,y) 是抛物线上一点,则M 到F的距离为
则M到直线l的距离为
所以
上式两边平方,整理可得y = 2px ①
根据抛物线的几何特征,如图,取经过点F且垂直于l的直线为x 轴,线
段KF的垂直平分线为y 轴,建立平面直角坐标系,此时,抛物线的焦点
抛物线及其标准方程
,准线为
为F
抛物线及其标准方程
从上述过程可以看到,抛物线上任意一点的坐标(x,y)都是方程①的解,以方 程①的解为坐标的点(x,y)与抛物线的焦点 的距离和它到准线 的 距离相等,即以方程①的解为坐标的点都在抛物线上,我们把方程①叫做抛物线 的标准方程,它表示焦点在x轴正半轴上,焦点是 ,准线是 的抛物
线 .
抛物线及其标准方程
在建立椭圆、双曲线的标准方程时,选择不同的坐标系我们得到了不同形 式的标准方程,抛物线的标准方程有哪些不同的形式 请探究之后填写下表.
图像 标准方程 焦点坐标 准线方程
y =2px(p>0) F(2,0) x=-2 y =-2px(p>0) F(-2,0) x=2 x =2py(p>0) F(0,2) y=-2 x =-2py(p>0) F(0,-2 y=2
1.标准方程特征:等号一边是某个变量的完全平方,等号的另一边是
另一变量的一次项;
2.标准方程中p 表示焦点到准线的距离,p 的值永远大于零;
3.四个标准方程的区分:焦点在一次项变量对应的坐标轴上,开口方 向由一次项系数的符号确定.当系数为正时,开口向坐标轴的正方向; 当系数为负时,开口向坐标轴的负方向.
抛物线及其标准方程
03 双曲线及其标准方程应用
P A R T 0 N E
例1. (1)已知抛物线的标准方程是y =6x, 求它的焦点坐标和准线方程;
(2)已知抛物线的焦点是F(0,-2), 求它的标准方程 .
抛物线及其标准方程
解:(1)∵抛物线的标准方程是y =6x,
,准线方程为
∴p=3, 抛物线的开口向右,焦点坐标
(2)∵抛物线的焦点是F(0,-2),
∴抛物线的标准方程为x =-8y.
∴焦点在x 轴的负半轴上,
即p=4,
练习:求满足下列条件的抛物线的标准方程.
(1)过点(一2,3);
(2)焦点在直线x —y+2=0 上 .
解:(1)设抛物线方程为x =2py 或y =—2px(p>0).
将点(一2,3)代入抛物线方程x =2py, 得
将点(一2,3)代入抛物线方程y 得
抛物线及其标准方程
∴满足条件的抛物线的标准方程为
(2)直线x—y+2=0 与两坐标轴的交点为(一2,0),(0,2). 若抛物线的焦点为(一2,0),设其方程为y =—2px(p>0).
抛物线及其标准方程
若抛物线的焦点为(0,2),设其方程为x =2py(p>0).
得—2p=—8, 所求方程为y =—8x;
得 2p=8, 所求方程为x =8y.
由
设方程 根据焦点位置(或开口方向),设出标准方程
列方程 根据条件建立关于参数p的方程
解方程 解关于参数p的方程,求出p的值
得方程 根据参数p的值,写出所求的标准方程
抛物线及其标准方程
方法总结
1.用待定系数法求抛物线标准方程的步骤
抛物线及其标准方程
2.求抛物线的标准方程时需注意的三个问题
(1)把握开口方向与方程一次项系数的对应关系;
(2)当抛物线的位置没有确定时,
可设方程为y =mx(m≠0) 或x =ny(n≠0),
(3)注意p 与p的 几 何 意 义 .
抛物线及其标准方程
例2.求下列抛物线的焦点坐标和准线方程:
(1)y =—14x;(2)5x —2y=0;(3)y =ax(a>0).
解:(1)因为p=7, 所以焦点坐标 准线方程是
(2)抛物线方程化为标准形式为 因为 所以焦点坐标 准线方程是
(3)由a>0 知 所以焦点坐标; 准线方程是
当a>0 时,焦点坐标 准线方程是
当a<0 时,焦点坐标 准线方程是
综上知,所求抛物线的焦点坐标为 准线方程为
练习:求抛物线y=ax (a≠0) 的焦点坐标和准线方程.
解 :把抛物线方程y = ax 化成标准方程
抛物线及其标准方程
例3.若F 是抛物线y =2x 的焦点,A,B 是该抛物线上的两点, |AF|+|BF|=6,
5
则线段AB的中点到y 轴的距离为 2
解:设 A(x ,y ),B(x , y ), 由抛物线的定义,可得
∵p=1,∴x +x =5,∴ 线 段AB 的中点的横坐标
∴线段AB的中点到y 轴 的 距 离
抛物线及其标准方程
练习:(1)从抛物线y =4x 上 一 点P 引抛物线准线的垂线,垂足为M, 且 |PM|=
5.设抛物线焦点为F, 则 △MPF 的面积为 10
解: ∵y =4x,∴F(1,0), 准线是x=—1.
∵|PM|=5,∴xp=4,∴|ypl=4.
抛物线及其标准方程
(2)已知抛物线的顶点在原点,焦点在x 轴上,抛物线上的点M ( 一 3,m)到焦点的
距离等于5,求抛物线的方程和m 的值.
解:方法一:根据已知条件,应设抛物线方程为
y =—2px(p>0), 则焦点为
∵点M(—3,m) 在抛物线上,且|MF|=5,
抛物线及其标准方程
方法二:由已知条件,设抛物线的方程为y =—2px(p>0),
则准线方程为
∵M(—3,m) 是抛物线上的点,根据抛物线定义,M 点到焦点的距离等于M
抛物线及其标准方程
点到准线的距离, , ∴p=4.
∴.抛物线的方程为y =—8x,m 的值为±2 √6.
解 或
∴所求的抛物线的方程为y =—8x.
又点M(—3,m) 在抛物线上, 故m = (一8)×(—3)=24.
∴m=±2√6.
抛物线及其标准方程
抛物线及其标准方程
例4.一种卫星接收天线如图3.3-3左图所示,其曲面与轴截面的交线为抛物线.在轴截面内的卫星 波束呈近似平行状态射入形为抛物线的接收天线,经反射聚集到焦点处,如图3.3-3(1).已知接收 天线的口径(直径)为4.8m,深度为 1m. 试建立适当的坐标系,求抛物线的标准方程和焦点坐标.
解:在接收天线的轴截面所在的平面建立直角坐标系,使接收天线的顶点(即抛物线的顶点)
与原点重合,焦点在x 轴上,如图所示,
∵点A(1,2.4)在抛物线y =2px 上,
故抛物线方程的标准方程为y =5.76x, 焦点坐标是(1.44,0).
04课堂小结
R T 0
抛物线定义
抛物线标准方程
抛物线方程应用
课堂小结
抛物线及其标准方程
人教A 版2019选修第一册
第三章圆锥曲线的方程
3.3.1 抛物线及其标准方程
学习目标
1.掌握抛物线的定义及焦点、准线的概念.
2.掌握抛物线的标准方程及其推导过程.
3.明确p的几何意义,并能解决简单的求抛物线标准方程问题.
01情景导入
P A R T 0 N E
(1)椭圆的离心率范围为0
(3)当e=1 时,它的轨迹是什么 抛物线
我们已经学习了圆、椭圆、双曲线三种圆锥曲线,今天我们类比椭圆、 双曲线的研究过程与方法,研究另一类圆锥曲线——抛物线.
情景导入
02抛物线及其标准方程
P A R T 0 N E
抛物线及其标准方程
作图1:
作定点F, 定直线l(不经过定点 F),B 为定直线上一个动点,过B作 l ⊥l, 线 段BF的垂直平分线交l 于D 点.拖动B点,点D随之运动。
思考:D 点满足什么条件 它的轨迹是什么 形状
抛物线及其标准方程
思考:D 点满足什么条件 它的轨迹是什么形状
在运动过程中,始终有|BD|=|DF|, 即 点D 与定点F的距离等于它到 定直线的距离,点D的轨迹形状与二次函数的图象相似。
作图2:
如图,我们在黑板上画一条直线EF, 然后取一个三角 板,将一条拉链AB固定在三角板的一条直角边上,并将拉 链下边一半的一端固定在C点,将三角板的另一条直角边 贴在直线EF 上,在拉锁D 处放置一支粉笔,上下拖动三角 板,粉笔会画出一条曲线.
抛物线及其标准方程
抛物线及其标准方程
问题1: |DA| 是点D 到直线EF 的距离吗 为什么 提示:是 .AB是直角三角形的一条直角边.
问题2:点D 在移动过程中,满足什么条件 提示:| DA|=|DC|.
问题3:画出的曲线是什么形状
提示:抛物线.
抛物线及其标准方程
抛物线定义
平面内到一个定点F 和一条定直线l( l 不经过点F) 的距离相等的点的轨迹叫做抛 物 线
定点F 叫做抛物线的焦点 .
定直线l叫做抛物线的准 线.
集合表示:P={M||MF|=d},d 为点M 到准线l的距离
对抛物线定义的认识
(1)定义的实质可归结为“一动三定”;一个动点,设为M; 一个定点F 叫 做抛物线的焦点; 一条定直线l, 叫做抛物线的准线; 一个定值,即点M 与点 F 的距离和它到直线l的距离之比等于1.
(2)注意定点F 不在直线l上,否则动点M 的轨迹不是抛物线,而是过点F 垂直 于直线l的一条直线.
抛物线及其标准方程
抛物线及其标准方程
求轨迹方程
C P_
建立直角坐标系
使方程形式足够简洁 !
设M(x,y) 是抛物线上一点,则M 到F的距离为
则M到直线l的距离为
所以
上式两边平方,整理可得y = 2px ①
根据抛物线的几何特征,如图,取经过点F且垂直于l的直线为x 轴,线
段KF的垂直平分线为y 轴,建立平面直角坐标系,此时,抛物线的焦点
抛物线及其标准方程
,准线为
为F
抛物线及其标准方程
从上述过程可以看到,抛物线上任意一点的坐标(x,y)都是方程①的解,以方 程①的解为坐标的点(x,y)与抛物线的焦点 的距离和它到准线 的 距离相等,即以方程①的解为坐标的点都在抛物线上,我们把方程①叫做抛物线 的标准方程,它表示焦点在x轴正半轴上,焦点是 ,准线是 的抛物
线 .
抛物线及其标准方程
在建立椭圆、双曲线的标准方程时,选择不同的坐标系我们得到了不同形 式的标准方程,抛物线的标准方程有哪些不同的形式 请探究之后填写下表.
图像 标准方程 焦点坐标 准线方程
y =2px(p>0) F(2,0) x=-2 y =-2px(p>0) F(-2,0) x=2 x =2py(p>0) F(0,2) y=-2 x =-2py(p>0) F(0,-2 y=2
1.标准方程特征:等号一边是某个变量的完全平方,等号的另一边是
另一变量的一次项;
2.标准方程中p 表示焦点到准线的距离,p 的值永远大于零;
3.四个标准方程的区分:焦点在一次项变量对应的坐标轴上,开口方 向由一次项系数的符号确定.当系数为正时,开口向坐标轴的正方向; 当系数为负时,开口向坐标轴的负方向.
抛物线及其标准方程
03 双曲线及其标准方程应用
P A R T 0 N E
例1. (1)已知抛物线的标准方程是y =6x, 求它的焦点坐标和准线方程;
(2)已知抛物线的焦点是F(0,-2), 求它的标准方程 .
抛物线及其标准方程
解:(1)∵抛物线的标准方程是y =6x,
,准线方程为
∴p=3, 抛物线的开口向右,焦点坐标
(2)∵抛物线的焦点是F(0,-2),
∴抛物线的标准方程为x =-8y.
∴焦点在x 轴的负半轴上,
即p=4,
练习:求满足下列条件的抛物线的标准方程.
(1)过点(一2,3);
(2)焦点在直线x —y+2=0 上 .
解:(1)设抛物线方程为x =2py 或y =—2px(p>0).
将点(一2,3)代入抛物线方程x =2py, 得
将点(一2,3)代入抛物线方程y 得
抛物线及其标准方程
∴满足条件的抛物线的标准方程为
(2)直线x—y+2=0 与两坐标轴的交点为(一2,0),(0,2). 若抛物线的焦点为(一2,0),设其方程为y =—2px(p>0).
抛物线及其标准方程
若抛物线的焦点为(0,2),设其方程为x =2py(p>0).
得—2p=—8, 所求方程为y =—8x;
得 2p=8, 所求方程为x =8y.
由
设方程 根据焦点位置(或开口方向),设出标准方程
列方程 根据条件建立关于参数p的方程
解方程 解关于参数p的方程,求出p的值
得方程 根据参数p的值,写出所求的标准方程
抛物线及其标准方程
方法总结
1.用待定系数法求抛物线标准方程的步骤
抛物线及其标准方程
2.求抛物线的标准方程时需注意的三个问题
(1)把握开口方向与方程一次项系数的对应关系;
(2)当抛物线的位置没有确定时,
可设方程为y =mx(m≠0) 或x =ny(n≠0),
(3)注意p 与p的 几 何 意 义 .
抛物线及其标准方程
例2.求下列抛物线的焦点坐标和准线方程:
(1)y =—14x;(2)5x —2y=0;(3)y =ax(a>0).
解:(1)因为p=7, 所以焦点坐标 准线方程是
(2)抛物线方程化为标准形式为 因为 所以焦点坐标 准线方程是
(3)由a>0 知 所以焦点坐标; 准线方程是
当a>0 时,焦点坐标 准线方程是
当a<0 时,焦点坐标 准线方程是
综上知,所求抛物线的焦点坐标为 准线方程为
练习:求抛物线y=ax (a≠0) 的焦点坐标和准线方程.
解 :把抛物线方程y = ax 化成标准方程
抛物线及其标准方程
例3.若F 是抛物线y =2x 的焦点,A,B 是该抛物线上的两点, |AF|+|BF|=6,
5
则线段AB的中点到y 轴的距离为 2
解:设 A(x ,y ),B(x , y ), 由抛物线的定义,可得
∵p=1,∴x +x =5,∴ 线 段AB 的中点的横坐标
∴线段AB的中点到y 轴 的 距 离
抛物线及其标准方程
练习:(1)从抛物线y =4x 上 一 点P 引抛物线准线的垂线,垂足为M, 且 |PM|=
5.设抛物线焦点为F, 则 △MPF 的面积为 10
解: ∵y =4x,∴F(1,0), 准线是x=—1.
∵|PM|=5,∴xp=4,∴|ypl=4.
抛物线及其标准方程
(2)已知抛物线的顶点在原点,焦点在x 轴上,抛物线上的点M ( 一 3,m)到焦点的
距离等于5,求抛物线的方程和m 的值.
解:方法一:根据已知条件,应设抛物线方程为
y =—2px(p>0), 则焦点为
∵点M(—3,m) 在抛物线上,且|MF|=5,
抛物线及其标准方程
方法二:由已知条件,设抛物线的方程为y =—2px(p>0),
则准线方程为
∵M(—3,m) 是抛物线上的点,根据抛物线定义,M 点到焦点的距离等于M
抛物线及其标准方程
点到准线的距离, , ∴p=4.
∴.抛物线的方程为y =—8x,m 的值为±2 √6.
解 或
∴所求的抛物线的方程为y =—8x.
又点M(—3,m) 在抛物线上, 故m = (一8)×(—3)=24.
∴m=±2√6.
抛物线及其标准方程
抛物线及其标准方程
例4.一种卫星接收天线如图3.3-3左图所示,其曲面与轴截面的交线为抛物线.在轴截面内的卫星 波束呈近似平行状态射入形为抛物线的接收天线,经反射聚集到焦点处,如图3.3-3(1).已知接收 天线的口径(直径)为4.8m,深度为 1m. 试建立适当的坐标系,求抛物线的标准方程和焦点坐标.
解:在接收天线的轴截面所在的平面建立直角坐标系,使接收天线的顶点(即抛物线的顶点)
与原点重合,焦点在x 轴上,如图所示,
∵点A(1,2.4)在抛物线y =2px 上,
故抛物线方程的标准方程为y =5.76x, 焦点坐标是(1.44,0).
04课堂小结
R T 0
抛物线定义
抛物线标准方程
抛物线方程应用
课堂小结
抛物线及其标准方程
