3.3.2 抛物线的简单几何性质 课件(共30张PPT)—— 高中数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 3.3.2 抛物线的简单几何性质 课件(共30张PPT)—— 高中数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 22:17:14 | ||
图片预览










文档简介
(共30张PPT)
第三章圆锥曲线的方程
3.3.2抛物线的简单几何性质
1.理解抛物线的简单几何性质(范围、对称性、顶点、
离心率) .
2.能用抛物线的简单几何性质解决一些简单的问题.
学习目标
1.范 围
因为p>0, 由方程y =2px 可知,对于抛物线上的点M(x,y),x...0,y∈ R, 当x>0 时,抛物线在y 轴的右侧,开口方向与x 轴的正方向相同;当x 的值增大时, Iyl的值也增大,这说明抛物线向右上方和右下方无限延伸
以 -y 代 y, 方 程y =2px(p>0) 不变,所以抛物线关于x 轴对称.抛物线的对
称轴叫做抛物线的轴.
2 对称性
3.顶点
抛物线和它的轴的交点叫做抛物线的顶点.在方程y =2px(p>0) 中,当x=0 时 ,y=0, 因此抛物线的顶点就是原点.
抛物线上的点M 与焦点F 的距离和点M 到准线的距离d 的比 ,叫做抛物
线的离心率,用e表示.由抛物线的定义可知,e=1.
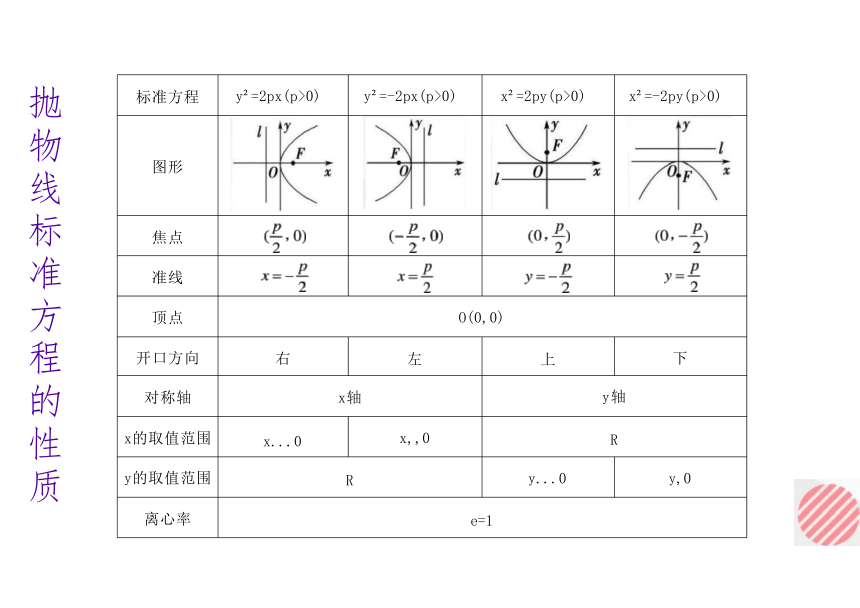
标准方程 y =2px(p>0) y =-2px(p>0) x =2py(p>0)
x =-2py(p>0)
图形
焦点
准线
顶点 O(0,0)
开口方向 右 左 上
下
对称轴 x轴 y轴
x的取值范围 x...0 x,,0 R
y的取值范围 R y...0
y,0
离心率 e=1
抛物线标准方程的性质
解:因为抛物线关于x 轴对称,它的顶点在原点,并且经过点M( 2,-2√2),
所以可设它的标准方程为y =2px(p> 0).
因为点M 在抛物线上,所以(-2√2) =2p×2, 解得p=2.
因此,所求抛物线的标准方程是y =4x.
例1已知抛物线关于x 轴对称,它的顶点在原点,并且经过点M(2,-2 √2),
求它的标准方程.
例题巩固
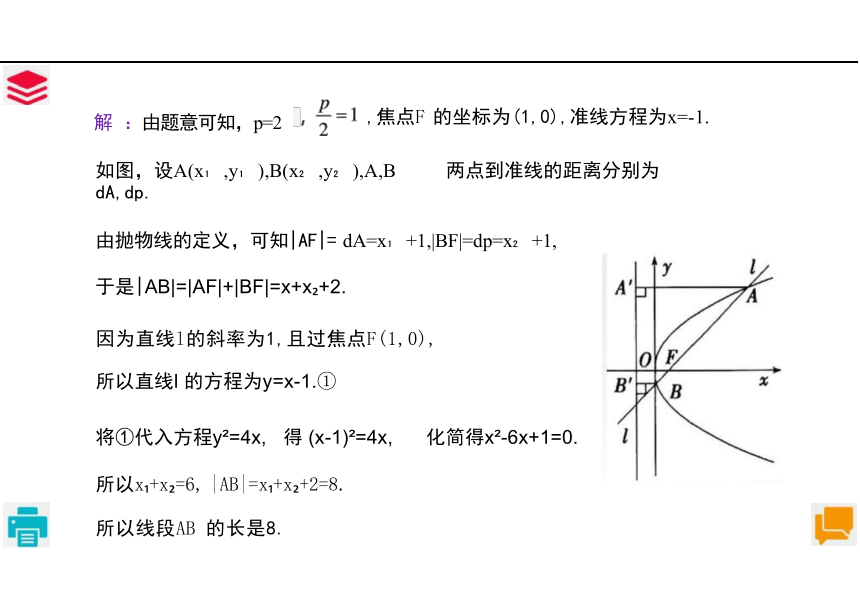
例2斜率为1的直线l 经过抛物线y =4x 的焦点F, 且与抛物线相交于A,B
两点,求线段 AB的长.
如图,设A(x ,y ),B(x ,y ),A,B 两点到准线的距离分别为dA,dp.
由抛物线的定义,可知|AF|= dA=x +1,|BF|=dp=x +1,
于是|AB|=|AF|+|BF|=x+x +2.
因为直线l的斜率为1,且过焦点F(1,0),
所以直线l 的方程为y=x-1.①
将①代入方程y =4x, 得 (x-1) =4x, 化简得x -6x+1=0.
所以x +x =6, |AB|=x +x +2=8.
所以线段AB 的长是8.
,焦点F 的坐标为(1,0),准线方程为x=-1.
解 :由题意可知,p=2
例3经过抛物线焦点F 的直线交抛物线于A,B 两点,经过点A和抛物线顶点
的直线交抛物线的准线于点D, 求证:直线DB 平行于抛物线的对称轴.
点A 的坐标为 ,则直线OA 的方程为
抛物线的准线方程是 ,联立②③可得点D 的纵坐标为
因为焦点F 的坐标是
当y ≠p 时,直线AF 的方程为
联立①④, 消 去x得y y -(y -p )y-y p =0, 即 (y-y )(y y+p )=0, 可得点B 的纵坐标为 ,与点D 的纵坐标相等,于是DB 平行于x 轴 .
当y =p 时,易知结论成立.
所以,直线DB 平行于抛物线的对称轴.
解:如图,以抛物线的对称轴为x 轴,抛物线的顶点为原点,建立平面直角坐
标系xOy.设抛物线的方程为y =2px(p>0)①,
例4如图,已知定点B(a,-h),BC⊥x 轴于点C,M 是线段OB上任意一点,
MD⊥x轴于点D,ME⊥BC 于点E,OE 与MD相交于点P, 求点P 的轨迹方程.
解:设点P(x,y),M(x,m), 其中0刻x a,则 点E 的坐标为(a,m).
由题意,直线OB 的方程为 ,①
因为点M 在 OB上,将点M的坐标代入①, ,②
所以点P 的横坐标x满足②.
直线OE 的方程为 ,③
因为点P 在OE 上,所以点P 的坐标(x,y)满足③ .
将②代入③,消去m得 劉 x a), 即点P 的轨迹方程.
课堂小练
1.已知A 为抛物线C:y =2px(p>0) 上的一点,点A 到抛物线C 的焦点的距离为12,
到 y 轴的距离为9,则p 的值为(C
A.2 B.3 C.6 D.9
解析:由抛物线定义知点A 到抛物线C 的焦点的距离等于到准线 的距离,
解得p=6. 故选C.
解析:设抛物线的焦点为F, 过P 作PA 与抛物线的准线x=-1 垂直,垂足为A,
作PB 与l 垂直,垂足为B, 则 d +d =PA|+|PB|-1=PF|+|PB|-1, 显然当
P,F,B 三点共线(即点P 在线段BF 上 ) 时 ,d +d 取得最小值,最小值为
.故选D.
2. 已知抛物线y =4x 和直线l:x-y+4=0, 在抛物线上有一动点P 到 y 轴的距离为
d, 到直线1的距离为d , 则 d,+d 的最小值为(D
A
解析:由题意可知过焦点 且倾斜角为60°的直线方程为 与
抛物线方程联立得 消去y 并整理,得 设点
A(x,y),B(x,y ), 则 解
得p=3. 故选C.
若线段AB的长为8,则p 的值为( C )
A.-3 B.1 C.3 D.4
3.过抛物线y =2px(p>0) 的焦点F 作倾斜角为60°的直线交抛物线于A,B 两点,
4.已知抛物线M 的顶点在原点,焦点在y轴正半轴上,过其焦点F 作直线l交抛物
线于A,B 两点,过点A,B 分别作抛物线准线的垂线,垂足分别为点C,D,
A.x =8y B.x =10y C.x =9y D.x =5y
|AF|=2|BFI, 且DC ·BA=72, 则该抛物线的方程为(
解析:设A(x,y ),B(x ,y ),x>x , 抛物线的方程为x =2py(p>0), 因 为
|AF|=2|BFI, 所以x =-2x , ,所以 ,y=p,x=√2p, 因为DC·BA=72, 所以 所以 p=4,
所以抛物线的方程为x =8y. 故选A.
5.过抛物线y =4x 焦点F 的直线交抛物线于A,B 两点,交其准线于点C, 且 A,C 位
于 x 轴同侧.若IACF=2|AFI, 则 IBFI=( C
A.2 B.3 C.4 D.5
解析:设抛物线y =4x 的准线为l, 准线l 与x 轴交于点H, 则 F(1,0),l:x=-1,
|HF|=p=2, 过 A 作AD⊥l, 垂足为D, 由抛物线的定义可知|AF 月ADI,
∵|AC|=2|AFI, AC|=2|ADI, 则I
,∴ ∴BF|=4, 故选C.
事
6. (多选)已知抛物线E:y =4x 的焦点为F, 准线为l, 过 F 的直线与E 交于A,
B 两 点 ,C,D 分别为A,B 在1上的射影,且|AF|=3|BFI,M 为 AB中点,则下
列结论正确的是(
A. ∠CFD=90° B. △CMD 为等腰直角三角形
C.直线AB 的斜率为±√3 D.△AOB 的面积为4
选项A中 ,C(-1,y),D(-1,y ),∴FC·FD=4+y y =4-4=0, 从而∠CFD=90°,
故A 正确;选项B 中 ,M(2m +1,2m),∴CM·DM=4(m +1) +4m -2m(y+y )
结合图形知△CMD 不是直角三角形,故B 错误;
∴y+y =4m,y ·y =-4, 从而x +x =4m +2,x ·x =1, 又 IAF=3|BFI,
解析:由y =4x, 得 2p=4, 即 p=2,∴ 焦点F(1,0),准线l:x=-1.
设直线AB的方程为x=my+1,A(x,y ),B(x ,y ), 由
即x=3x +2, 因此x =m , 且3x +2x -1=0→
即直线AB的斜率为±√3,故C 正确;
故D 错误.故选AC.
或
x =-1 (舍去),
,得y -4my-4=0
选项D 中,
: ·
,
解析:因为点A 在抛物线上,所以3=2mp, 点A到抛物线准线的距离为
,解得 或 p=6, 当 p=6 时, ,不符合题意,舍
7.若抛物线x =2py(p>0) 上一点A(√3,m)(m>1) 到抛物线准线的距离为
则抛物线的方程为_
故抛物线的方程为x =y.
去,所以
事
8.已知抛物线C:y =8x, 点 P 为抛物线上任意一点,过点P 向 圆D:x +y -4x+3
=0作切线,切点分别为A,B, 则四边形PADB的面积的最小值为
解析:如图,连接PD, 圆 D:(x-2) +y =1, 该圆的圆心与抛物线的焦点重合,
半径为1,则S 四边形PADB=2SI△PAp=|PA|.又|PAF=√ {PDI -1, 所以当四边形PADB 的面积最小时, |PDI 最小.过点P 向抛物线的准线x=-2 作垂线,垂足为E, 则
|PD=|PE|, 当 点P 与坐标原点重合时, |PEI最小,此时|PEI=2. 故
9.已知抛物线C:y =2px(p>0) 的焦点为F, 点 P(xo,√2p) 在抛物线C 上,且
|PF|=3.
(1)求抛物线C 的方程;
(2)过焦点F 的直线l 与抛物线分别交于A,B 两点,点A,B 的坐标分别为(x,y ), (x ,y ),O 为坐标原点,若OA·OB=-(x+x ), 求 直 线l 的方程.
解析:(1)由点P(x ,√2p) 在抛物线C 上,
得( √2p) =2px , 解得x =p,
由抛物线定义得, 解得p=2,
故抛物线C 的方程为y =4x.
联立 消去x, 得 y -4my-4=0,
故y +y =4m,y y =-4,
所以 ,x+x =(my +1)+(my +1)=m(y +y )+2=4m +2,
则OA·OB=-(x +x )=xx +y y =-3, 即 4m +2=3, 解得 所以所求直线l 的方程为y=2x-2 或 y=2-2x.
(2)设直线1的方程为x=my+1,
小结:
回顾一下本节课学习了哪些新知识呢
1.范围
2.对称性
3.顶点
4.离心率
第三章圆锥曲线的方程
3.3.2抛物线的简单几何性质
1.理解抛物线的简单几何性质(范围、对称性、顶点、
离心率) .
2.能用抛物线的简单几何性质解决一些简单的问题.
学习目标
1.范 围
因为p>0, 由方程y =2px 可知,对于抛物线上的点M(x,y),x...0,y∈ R, 当x>0 时,抛物线在y 轴的右侧,开口方向与x 轴的正方向相同;当x 的值增大时, Iyl的值也增大,这说明抛物线向右上方和右下方无限延伸
以 -y 代 y, 方 程y =2px(p>0) 不变,所以抛物线关于x 轴对称.抛物线的对
称轴叫做抛物线的轴.
2 对称性
3.顶点
抛物线和它的轴的交点叫做抛物线的顶点.在方程y =2px(p>0) 中,当x=0 时 ,y=0, 因此抛物线的顶点就是原点.
抛物线上的点M 与焦点F 的距离和点M 到准线的距离d 的比 ,叫做抛物
线的离心率,用e表示.由抛物线的定义可知,e=1.
标准方程 y =2px(p>0) y =-2px(p>0) x =2py(p>0)
x =-2py(p>0)
图形
焦点
准线
顶点 O(0,0)
开口方向 右 左 上
下
对称轴 x轴 y轴
x的取值范围 x...0 x,,0 R
y的取值范围 R y...0
y,0
离心率 e=1
抛物线标准方程的性质
解:因为抛物线关于x 轴对称,它的顶点在原点,并且经过点M( 2,-2√2),
所以可设它的标准方程为y =2px(p> 0).
因为点M 在抛物线上,所以(-2√2) =2p×2, 解得p=2.
因此,所求抛物线的标准方程是y =4x.
例1已知抛物线关于x 轴对称,它的顶点在原点,并且经过点M(2,-2 √2),
求它的标准方程.
例题巩固
例2斜率为1的直线l 经过抛物线y =4x 的焦点F, 且与抛物线相交于A,B
两点,求线段 AB的长.
如图,设A(x ,y ),B(x ,y ),A,B 两点到准线的距离分别为dA,dp.
由抛物线的定义,可知|AF|= dA=x +1,|BF|=dp=x +1,
于是|AB|=|AF|+|BF|=x+x +2.
因为直线l的斜率为1,且过焦点F(1,0),
所以直线l 的方程为y=x-1.①
将①代入方程y =4x, 得 (x-1) =4x, 化简得x -6x+1=0.
所以x +x =6, |AB|=x +x +2=8.
所以线段AB 的长是8.
,焦点F 的坐标为(1,0),准线方程为x=-1.
解 :由题意可知,p=2
例3经过抛物线焦点F 的直线交抛物线于A,B 两点,经过点A和抛物线顶点
的直线交抛物线的准线于点D, 求证:直线DB 平行于抛物线的对称轴.
点A 的坐标为 ,则直线OA 的方程为
抛物线的准线方程是 ,联立②③可得点D 的纵坐标为
因为焦点F 的坐标是
当y ≠p 时,直线AF 的方程为
联立①④, 消 去x得y y -(y -p )y-y p =0, 即 (y-y )(y y+p )=0, 可得点B 的纵坐标为 ,与点D 的纵坐标相等,于是DB 平行于x 轴 .
当y =p 时,易知结论成立.
所以,直线DB 平行于抛物线的对称轴.
解:如图,以抛物线的对称轴为x 轴,抛物线的顶点为原点,建立平面直角坐
标系xOy.设抛物线的方程为y =2px(p>0)①,
例4如图,已知定点B(a,-h),BC⊥x 轴于点C,M 是线段OB上任意一点,
MD⊥x轴于点D,ME⊥BC 于点E,OE 与MD相交于点P, 求点P 的轨迹方程.
解:设点P(x,y),M(x,m), 其中0刻x a,则 点E 的坐标为(a,m).
由题意,直线OB 的方程为 ,①
因为点M 在 OB上,将点M的坐标代入①, ,②
所以点P 的横坐标x满足②.
直线OE 的方程为 ,③
因为点P 在OE 上,所以点P 的坐标(x,y)满足③ .
将②代入③,消去m得 劉 x a), 即点P 的轨迹方程.
课堂小练
1.已知A 为抛物线C:y =2px(p>0) 上的一点,点A 到抛物线C 的焦点的距离为12,
到 y 轴的距离为9,则p 的值为(C
A.2 B.3 C.6 D.9
解析:由抛物线定义知点A 到抛物线C 的焦点的距离等于到准线 的距离,
解得p=6. 故选C.
解析:设抛物线的焦点为F, 过P 作PA 与抛物线的准线x=-1 垂直,垂足为A,
作PB 与l 垂直,垂足为B, 则 d +d =PA|+|PB|-1=PF|+|PB|-1, 显然当
P,F,B 三点共线(即点P 在线段BF 上 ) 时 ,d +d 取得最小值,最小值为
.故选D.
2. 已知抛物线y =4x 和直线l:x-y+4=0, 在抛物线上有一动点P 到 y 轴的距离为
d, 到直线1的距离为d , 则 d,+d 的最小值为(D
A
解析:由题意可知过焦点 且倾斜角为60°的直线方程为 与
抛物线方程联立得 消去y 并整理,得 设点
A(x,y),B(x,y ), 则 解
得p=3. 故选C.
若线段AB的长为8,则p 的值为( C )
A.-3 B.1 C.3 D.4
3.过抛物线y =2px(p>0) 的焦点F 作倾斜角为60°的直线交抛物线于A,B 两点,
4.已知抛物线M 的顶点在原点,焦点在y轴正半轴上,过其焦点F 作直线l交抛物
线于A,B 两点,过点A,B 分别作抛物线准线的垂线,垂足分别为点C,D,
A.x =8y B.x =10y C.x =9y D.x =5y
|AF|=2|BFI, 且DC ·BA=72, 则该抛物线的方程为(
解析:设A(x,y ),B(x ,y ),x>x , 抛物线的方程为x =2py(p>0), 因 为
|AF|=2|BFI, 所以x =-2x , ,所以 ,y=p,x=√2p, 因为DC·BA=72, 所以 所以 p=4,
所以抛物线的方程为x =8y. 故选A.
5.过抛物线y =4x 焦点F 的直线交抛物线于A,B 两点,交其准线于点C, 且 A,C 位
于 x 轴同侧.若IACF=2|AFI, 则 IBFI=( C
A.2 B.3 C.4 D.5
解析:设抛物线y =4x 的准线为l, 准线l 与x 轴交于点H, 则 F(1,0),l:x=-1,
|HF|=p=2, 过 A 作AD⊥l, 垂足为D, 由抛物线的定义可知|AF 月ADI,
∵|AC|=2|AFI, AC|=2|ADI, 则I
,∴ ∴BF|=4, 故选C.
事
6. (多选)已知抛物线E:y =4x 的焦点为F, 准线为l, 过 F 的直线与E 交于A,
B 两 点 ,C,D 分别为A,B 在1上的射影,且|AF|=3|BFI,M 为 AB中点,则下
列结论正确的是(
A. ∠CFD=90° B. △CMD 为等腰直角三角形
C.直线AB 的斜率为±√3 D.△AOB 的面积为4
选项A中 ,C(-1,y),D(-1,y ),∴FC·FD=4+y y =4-4=0, 从而∠CFD=90°,
故A 正确;选项B 中 ,M(2m +1,2m),∴CM·DM=4(m +1) +4m -2m(y+y )
结合图形知△CMD 不是直角三角形,故B 错误;
∴y+y =4m,y ·y =-4, 从而x +x =4m +2,x ·x =1, 又 IAF=3|BFI,
解析:由y =4x, 得 2p=4, 即 p=2,∴ 焦点F(1,0),准线l:x=-1.
设直线AB的方程为x=my+1,A(x,y ),B(x ,y ), 由
即x=3x +2, 因此x =m , 且3x +2x -1=0→
即直线AB的斜率为±√3,故C 正确;
故D 错误.故选AC.
或
x =-1 (舍去),
,得y -4my-4=0
选项D 中,
: ·
,
解析:因为点A 在抛物线上,所以3=2mp, 点A到抛物线准线的距离为
,解得 或 p=6, 当 p=6 时, ,不符合题意,舍
7.若抛物线x =2py(p>0) 上一点A(√3,m)(m>1) 到抛物线准线的距离为
则抛物线的方程为_
故抛物线的方程为x =y.
去,所以
事
8.已知抛物线C:y =8x, 点 P 为抛物线上任意一点,过点P 向 圆D:x +y -4x+3
=0作切线,切点分别为A,B, 则四边形PADB的面积的最小值为
解析:如图,连接PD, 圆 D:(x-2) +y =1, 该圆的圆心与抛物线的焦点重合,
半径为1,则S 四边形PADB=2SI△PAp=|PA|.又|PAF=√ {PDI -1, 所以当四边形PADB 的面积最小时, |PDI 最小.过点P 向抛物线的准线x=-2 作垂线,垂足为E, 则
|PD=|PE|, 当 点P 与坐标原点重合时, |PEI最小,此时|PEI=2. 故
9.已知抛物线C:y =2px(p>0) 的焦点为F, 点 P(xo,√2p) 在抛物线C 上,且
|PF|=3.
(1)求抛物线C 的方程;
(2)过焦点F 的直线l 与抛物线分别交于A,B 两点,点A,B 的坐标分别为(x,y ), (x ,y ),O 为坐标原点,若OA·OB=-(x+x ), 求 直 线l 的方程.
解析:(1)由点P(x ,√2p) 在抛物线C 上,
得( √2p) =2px , 解得x =p,
由抛物线定义得, 解得p=2,
故抛物线C 的方程为y =4x.
联立 消去x, 得 y -4my-4=0,
故y +y =4m,y y =-4,
所以 ,x+x =(my +1)+(my +1)=m(y +y )+2=4m +2,
则OA·OB=-(x +x )=xx +y y =-3, 即 4m +2=3, 解得 所以所求直线l 的方程为y=2x-2 或 y=2-2x.
(2)设直线1的方程为x=my+1,
小结:
回顾一下本节课学习了哪些新知识呢
1.范围
2.对称性
3.顶点
4.离心率
