【湘教版数学九年级上册同步练习】 期中复习综合题(含答案)
文档属性
| 名称 | 【湘教版数学九年级上册同步练习】 期中复习综合题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【湘教版数学九年级上册同步练习】
期中复习综合题
一、单选题
1.在比例尺是1:38000的黄浦江交通游览图上,某隧道长约7,它的实际长度约为( )
A.0.266; B.2.66; C.26.6; D.266.
2.已知(a、b不为0),那么下列等式不成立的是( )
A. B. C. D.
3.已知: , 则 的值为( )
A.3 B.2 C. D.
4.已知,若,则=( )
A.12 B.15 C.16 D.1
5.如图,△ABC中,DE∥BC,则下列等式中不成立的是( )
A. B. C. D.
二、填空题
6.已知,则 .
7.如图,小明用2m长的标杆测量一棵树的高度.根据图示条件,树高为 m.
8.在比例尺是的地图上测得A、B两点间的距离为2厘米,那么两地的实际距离为 千米.
9.已知:x:y=2:5,那么(x+y):y= .
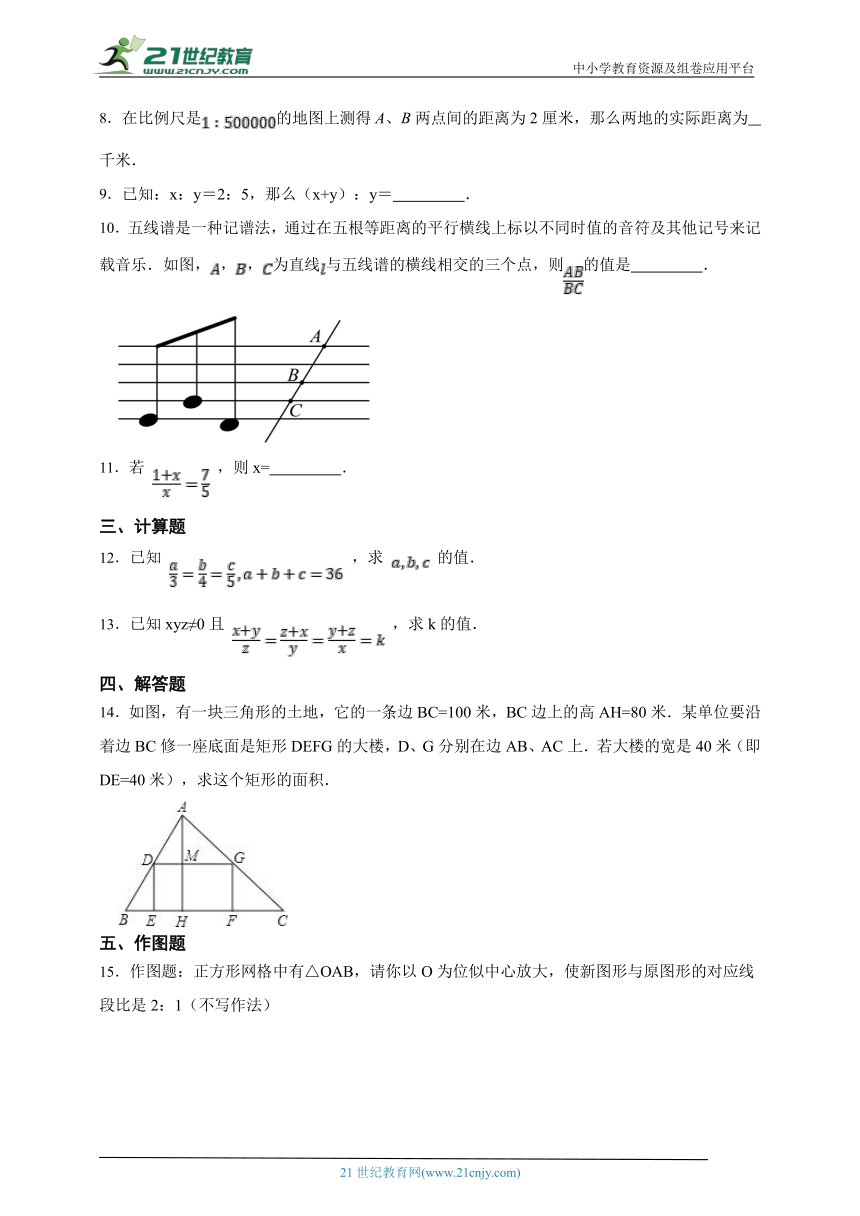
10.五线谱是一种记谱法,通过在五根等距离的平行横线上标以不同时值的音符及其他记号来记载音乐.如图,,,为直线与五线谱的横线相交的三个点,则的值是 .
11.若 ,则x= .
三、计算题
12.已知 ,求 的值.
13.已知xyz≠0且 ,求k的值.
四、解答题
14.如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),求这个矩形的面积.
五、作图题
15.作图题:正方形网格中有△OAB,请你以O为位似中心放大,使新图形与原图形的对应线段比是2:1(不写作法)
六、综合题
16.如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.
(1)求证:BC是∠ABE的平分线;
(2)若DC=8,⊙O的半径OA=6,求CE的长.
17.如图,已知AB∥CD,AD、BC 交于点E.
(1)写出所有比值等于 的两条线段之比.
(2)若AE=3,DE=6,BC=12,求CE的长.
18.在△ABC中,AB=12,点E在AC上,点D在AB上,若AE=6,EC=4, 。
(1)求AD的长;
(2)试问 能成立吗?请说明理由。
答案解析部分
1.【答案】B
【知识点】比例线段
2.【答案】D
【知识点】比例的性质
3.【答案】C
【知识点】比例的性质
4.【答案】A
【知识点】比例的性质
5.【答案】B
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
6.【答案】
【知识点】比例的性质
7.【答案】7
【知识点】两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的性质
8.【答案】10
【知识点】比例的性质;比例线段
9.【答案】7:5
【知识点】比例的性质
10.【答案】2
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
11.【答案】2.5
【知识点】比例的性质
12.【答案】解:设 (k≠0),则a=3k,b=4k,c=5k,依题意有3k+4k+5k=36,
解得k=3,
则a=3k=9,b=4k=12,c=5k=15.
【知识点】代数式求值;比例的性质
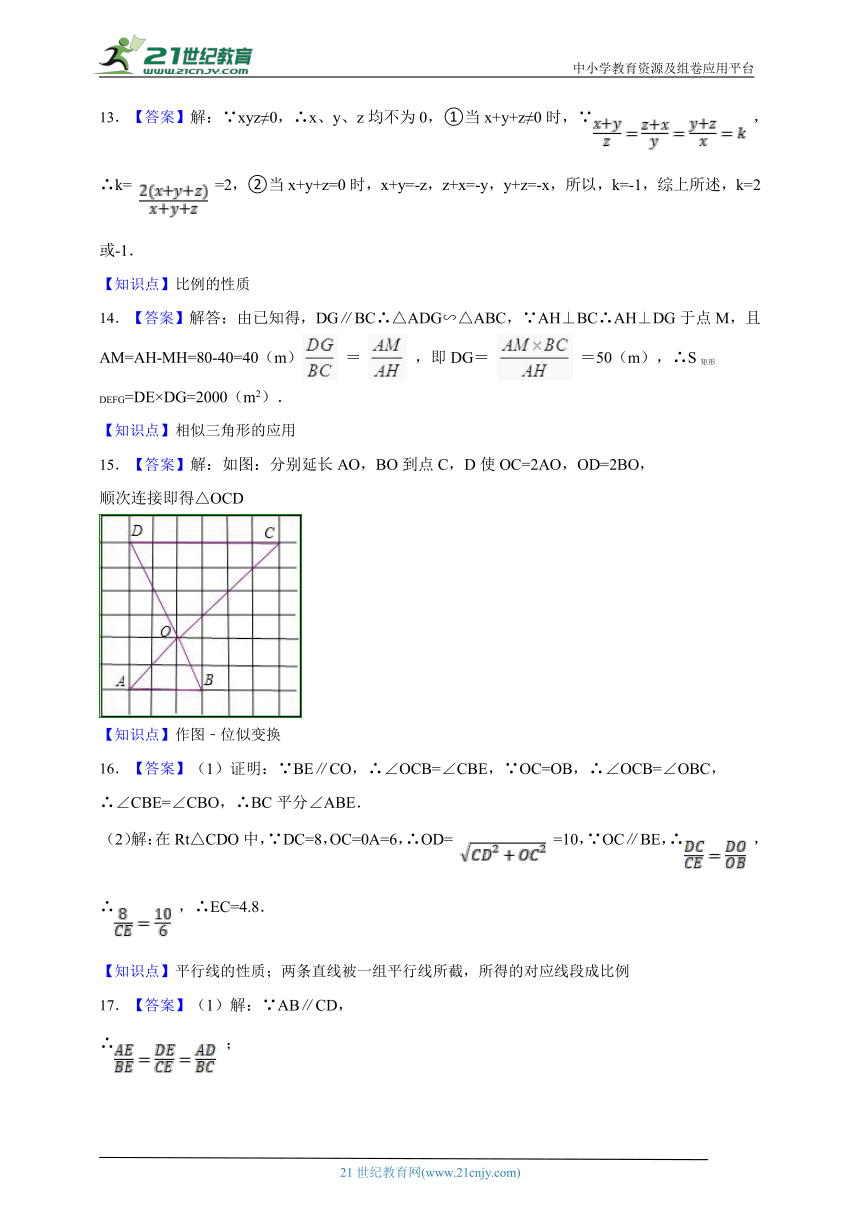
13.【答案】解:∵xyz≠0,∴x、y、z均不为0,①当x+y+z≠0时,∵ ,∴k= =2,②当x+y+z=0时,x+y=-z,z+x=-y,y+z=-x,所以,k=-1,综上所述,k=2或-1.
【知识点】比例的性质
14.【答案】解答:由已知得,DG∥BC∴△ADG∽△ABC,∵AH⊥BC∴AH⊥DG于点M,且AM=AH-MH=80-40=40(m) = ,即DG= =50(m),∴S矩形DEFG=DE×DG=2000(m2).
【知识点】相似三角形的应用
15.【答案】解:如图:分别延长AO,BO到点C,D使OC=2AO,OD=2BO,
顺次连接即得△OCD
【知识点】作图﹣位似变换
16.【答案】(1)证明:∵BE∥CO,∴∠OCB=∠CBE,∵OC=OB,∴∠OCB=∠OBC,∴∠CBE=∠CBO,∴BC平分∠ABE.
(2)解:在Rt△CDO中,∵DC=8,OC=0A=6,∴OD= =10,∵OC∥BE,∴ ,∴ ,∴EC=4.8.
【知识点】平行线的性质;两条直线被一组平行线所截,所得的对应线段成比例
17.【答案】(1)解:∵AB∥CD,
∴;
∴等于 的两条线段之比有: DE:CE,AD:BC.
(2)解:∵,
解得CE=8.
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
18.【答案】(1)解:设AD=x,则BD=AB-AD=(12-x)cm,
x:12-x=6:4,
解得x=7.2,
∴AD=7.2
(2)解:能,
由AB=12,AD= ,
故DB= .
于是 ,
又 ,
故 .
【知识点】比例线段
【湘教版数学九年级上册同步练习】
期中复习综合题
一、单选题
1.在比例尺是1:38000的黄浦江交通游览图上,某隧道长约7,它的实际长度约为( )
A.0.266; B.2.66; C.26.6; D.266.
2.已知(a、b不为0),那么下列等式不成立的是( )
A. B. C. D.
3.已知: , 则 的值为( )
A.3 B.2 C. D.
4.已知,若,则=( )
A.12 B.15 C.16 D.1
5.如图,△ABC中,DE∥BC,则下列等式中不成立的是( )
A. B. C. D.
二、填空题
6.已知,则 .
7.如图,小明用2m长的标杆测量一棵树的高度.根据图示条件,树高为 m.
8.在比例尺是的地图上测得A、B两点间的距离为2厘米,那么两地的实际距离为 千米.
9.已知:x:y=2:5,那么(x+y):y= .
10.五线谱是一种记谱法,通过在五根等距离的平行横线上标以不同时值的音符及其他记号来记载音乐.如图,,,为直线与五线谱的横线相交的三个点,则的值是 .
11.若 ,则x= .
三、计算题
12.已知 ,求 的值.
13.已知xyz≠0且 ,求k的值.
四、解答题
14.如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),求这个矩形的面积.
五、作图题
15.作图题:正方形网格中有△OAB,请你以O为位似中心放大,使新图形与原图形的对应线段比是2:1(不写作法)
六、综合题
16.如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.
(1)求证:BC是∠ABE的平分线;
(2)若DC=8,⊙O的半径OA=6,求CE的长.
17.如图,已知AB∥CD,AD、BC 交于点E.
(1)写出所有比值等于 的两条线段之比.
(2)若AE=3,DE=6,BC=12,求CE的长.
18.在△ABC中,AB=12,点E在AC上,点D在AB上,若AE=6,EC=4, 。
(1)求AD的长;
(2)试问 能成立吗?请说明理由。
答案解析部分
1.【答案】B
【知识点】比例线段
2.【答案】D
【知识点】比例的性质
3.【答案】C
【知识点】比例的性质
4.【答案】A
【知识点】比例的性质
5.【答案】B
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
6.【答案】
【知识点】比例的性质
7.【答案】7
【知识点】两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的性质
8.【答案】10
【知识点】比例的性质;比例线段
9.【答案】7:5
【知识点】比例的性质
10.【答案】2
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
11.【答案】2.5
【知识点】比例的性质
12.【答案】解:设 (k≠0),则a=3k,b=4k,c=5k,依题意有3k+4k+5k=36,
解得k=3,
则a=3k=9,b=4k=12,c=5k=15.
【知识点】代数式求值;比例的性质
13.【答案】解:∵xyz≠0,∴x、y、z均不为0,①当x+y+z≠0时,∵ ,∴k= =2,②当x+y+z=0时,x+y=-z,z+x=-y,y+z=-x,所以,k=-1,综上所述,k=2或-1.
【知识点】比例的性质
14.【答案】解答:由已知得,DG∥BC∴△ADG∽△ABC,∵AH⊥BC∴AH⊥DG于点M,且AM=AH-MH=80-40=40(m) = ,即DG= =50(m),∴S矩形DEFG=DE×DG=2000(m2).
【知识点】相似三角形的应用
15.【答案】解:如图:分别延长AO,BO到点C,D使OC=2AO,OD=2BO,
顺次连接即得△OCD
【知识点】作图﹣位似变换
16.【答案】(1)证明:∵BE∥CO,∴∠OCB=∠CBE,∵OC=OB,∴∠OCB=∠OBC,∴∠CBE=∠CBO,∴BC平分∠ABE.
(2)解:在Rt△CDO中,∵DC=8,OC=0A=6,∴OD= =10,∵OC∥BE,∴ ,∴ ,∴EC=4.8.
【知识点】平行线的性质;两条直线被一组平行线所截,所得的对应线段成比例
17.【答案】(1)解:∵AB∥CD,
∴;
∴等于 的两条线段之比有: DE:CE,AD:BC.
(2)解:∵,
解得CE=8.
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
18.【答案】(1)解:设AD=x,则BD=AB-AD=(12-x)cm,
x:12-x=6:4,
解得x=7.2,
∴AD=7.2
(2)解:能,
由AB=12,AD= ,
故DB= .
于是 ,
又 ,
故 .
【知识点】比例线段
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【湘教版数学九年级上册同步练习】
期中复习综合题
一、单选题
1.在比例尺是1:38000的黄浦江交通游览图上,某隧道长约7,它的实际长度约为( )
A.0.266; B.2.66; C.26.6; D.266.
2.已知(a、b不为0),那么下列等式不成立的是( )
A. B. C. D.
3.已知: , 则 的值为( )
A.3 B.2 C. D.
4.已知,若,则=( )
A.12 B.15 C.16 D.1
5.如图,△ABC中,DE∥BC,则下列等式中不成立的是( )
A. B. C. D.
二、填空题
6.已知,则 .
7.如图,小明用2m长的标杆测量一棵树的高度.根据图示条件,树高为 m.
8.在比例尺是的地图上测得A、B两点间的距离为2厘米,那么两地的实际距离为 千米.
9.已知:x:y=2:5,那么(x+y):y= .
10.五线谱是一种记谱法,通过在五根等距离的平行横线上标以不同时值的音符及其他记号来记载音乐.如图,,,为直线与五线谱的横线相交的三个点,则的值是 .
11.若 ,则x= .
三、计算题
12.已知 ,求 的值.
13.已知xyz≠0且 ,求k的值.
四、解答题
14.如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),求这个矩形的面积.
五、作图题
15.作图题:正方形网格中有△OAB,请你以O为位似中心放大,使新图形与原图形的对应线段比是2:1(不写作法)
六、综合题
16.如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.
(1)求证:BC是∠ABE的平分线;
(2)若DC=8,⊙O的半径OA=6,求CE的长.
17.如图,已知AB∥CD,AD、BC 交于点E.
(1)写出所有比值等于 的两条线段之比.
(2)若AE=3,DE=6,BC=12,求CE的长.
18.在△ABC中,AB=12,点E在AC上,点D在AB上,若AE=6,EC=4, 。
(1)求AD的长;
(2)试问 能成立吗?请说明理由。
答案解析部分
1.【答案】B
【知识点】比例线段
2.【答案】D
【知识点】比例的性质
3.【答案】C
【知识点】比例的性质
4.【答案】A
【知识点】比例的性质
5.【答案】B
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
6.【答案】
【知识点】比例的性质
7.【答案】7
【知识点】两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的性质
8.【答案】10
【知识点】比例的性质;比例线段
9.【答案】7:5
【知识点】比例的性质
10.【答案】2
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
11.【答案】2.5
【知识点】比例的性质
12.【答案】解:设 (k≠0),则a=3k,b=4k,c=5k,依题意有3k+4k+5k=36,
解得k=3,
则a=3k=9,b=4k=12,c=5k=15.
【知识点】代数式求值;比例的性质
13.【答案】解:∵xyz≠0,∴x、y、z均不为0,①当x+y+z≠0时,∵ ,∴k= =2,②当x+y+z=0时,x+y=-z,z+x=-y,y+z=-x,所以,k=-1,综上所述,k=2或-1.
【知识点】比例的性质
14.【答案】解答:由已知得,DG∥BC∴△ADG∽△ABC,∵AH⊥BC∴AH⊥DG于点M,且AM=AH-MH=80-40=40(m) = ,即DG= =50(m),∴S矩形DEFG=DE×DG=2000(m2).
【知识点】相似三角形的应用
15.【答案】解:如图:分别延长AO,BO到点C,D使OC=2AO,OD=2BO,
顺次连接即得△OCD
【知识点】作图﹣位似变换
16.【答案】(1)证明:∵BE∥CO,∴∠OCB=∠CBE,∵OC=OB,∴∠OCB=∠OBC,∴∠CBE=∠CBO,∴BC平分∠ABE.
(2)解:在Rt△CDO中,∵DC=8,OC=0A=6,∴OD= =10,∵OC∥BE,∴ ,∴ ,∴EC=4.8.
【知识点】平行线的性质;两条直线被一组平行线所截,所得的对应线段成比例
17.【答案】(1)解:∵AB∥CD,
∴;
∴等于 的两条线段之比有: DE:CE,AD:BC.
(2)解:∵,
解得CE=8.
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
18.【答案】(1)解:设AD=x,则BD=AB-AD=(12-x)cm,
x:12-x=6:4,
解得x=7.2,
∴AD=7.2
(2)解:能,
由AB=12,AD= ,
故DB= .
于是 ,
又 ,
故 .
【知识点】比例线段
【湘教版数学九年级上册同步练习】
期中复习综合题
一、单选题
1.在比例尺是1:38000的黄浦江交通游览图上,某隧道长约7,它的实际长度约为( )
A.0.266; B.2.66; C.26.6; D.266.
2.已知(a、b不为0),那么下列等式不成立的是( )
A. B. C. D.
3.已知: , 则 的值为( )
A.3 B.2 C. D.
4.已知,若,则=( )
A.12 B.15 C.16 D.1
5.如图,△ABC中,DE∥BC,则下列等式中不成立的是( )
A. B. C. D.
二、填空题
6.已知,则 .
7.如图,小明用2m长的标杆测量一棵树的高度.根据图示条件,树高为 m.
8.在比例尺是的地图上测得A、B两点间的距离为2厘米,那么两地的实际距离为 千米.
9.已知:x:y=2:5,那么(x+y):y= .
10.五线谱是一种记谱法,通过在五根等距离的平行横线上标以不同时值的音符及其他记号来记载音乐.如图,,,为直线与五线谱的横线相交的三个点,则的值是 .
11.若 ,则x= .
三、计算题
12.已知 ,求 的值.
13.已知xyz≠0且 ,求k的值.
四、解答题
14.如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),求这个矩形的面积.
五、作图题
15.作图题:正方形网格中有△OAB,请你以O为位似中心放大,使新图形与原图形的对应线段比是2:1(不写作法)
六、综合题
16.如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.
(1)求证:BC是∠ABE的平分线;
(2)若DC=8,⊙O的半径OA=6,求CE的长.
17.如图,已知AB∥CD,AD、BC 交于点E.
(1)写出所有比值等于 的两条线段之比.
(2)若AE=3,DE=6,BC=12,求CE的长.
18.在△ABC中,AB=12,点E在AC上,点D在AB上,若AE=6,EC=4, 。
(1)求AD的长;
(2)试问 能成立吗?请说明理由。
答案解析部分
1.【答案】B
【知识点】比例线段
2.【答案】D
【知识点】比例的性质
3.【答案】C
【知识点】比例的性质
4.【答案】A
【知识点】比例的性质
5.【答案】B
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
6.【答案】
【知识点】比例的性质
7.【答案】7
【知识点】两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的性质
8.【答案】10
【知识点】比例的性质;比例线段
9.【答案】7:5
【知识点】比例的性质
10.【答案】2
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
11.【答案】2.5
【知识点】比例的性质
12.【答案】解:设 (k≠0),则a=3k,b=4k,c=5k,依题意有3k+4k+5k=36,
解得k=3,
则a=3k=9,b=4k=12,c=5k=15.
【知识点】代数式求值;比例的性质
13.【答案】解:∵xyz≠0,∴x、y、z均不为0,①当x+y+z≠0时,∵ ,∴k= =2,②当x+y+z=0时,x+y=-z,z+x=-y,y+z=-x,所以,k=-1,综上所述,k=2或-1.
【知识点】比例的性质
14.【答案】解答:由已知得,DG∥BC∴△ADG∽△ABC,∵AH⊥BC∴AH⊥DG于点M,且AM=AH-MH=80-40=40(m) = ,即DG= =50(m),∴S矩形DEFG=DE×DG=2000(m2).
【知识点】相似三角形的应用
15.【答案】解:如图:分别延长AO,BO到点C,D使OC=2AO,OD=2BO,
顺次连接即得△OCD
【知识点】作图﹣位似变换
16.【答案】(1)证明:∵BE∥CO,∴∠OCB=∠CBE,∵OC=OB,∴∠OCB=∠OBC,∴∠CBE=∠CBO,∴BC平分∠ABE.
(2)解:在Rt△CDO中,∵DC=8,OC=0A=6,∴OD= =10,∵OC∥BE,∴ ,∴ ,∴EC=4.8.
【知识点】平行线的性质;两条直线被一组平行线所截,所得的对应线段成比例
17.【答案】(1)解:∵AB∥CD,
∴;
∴等于 的两条线段之比有: DE:CE,AD:BC.
(2)解:∵,
解得CE=8.
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
18.【答案】(1)解:设AD=x,则BD=AB-AD=(12-x)cm,
x:12-x=6:4,
解得x=7.2,
∴AD=7.2
(2)解:能,
由AB=12,AD= ,
故DB= .
于是 ,
又 ,
故 .
【知识点】比例线段
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
