数学人教A版(2019)选择性必修第一册 直线与圆的位置关系 课件(共38张PPT)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册 直线与圆的位置关系 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 00:00:00 | ||
图片预览







文档简介
(共38张PPT)
2.5.1直线与圆的位置关系
第一课时
素 养目 标
学 科 素 养
1.掌握直线与圆的三种位置关系:相交,相切, 相离;(重点) 2.会用代数法和几何法来判断直线与圆的三种位 置关系;(难点) 3.会用直线与圆的位置关系解决一些实际问 题. (重点、难点)
1、直观想象
2、数学运算
3、数形结合
学习目标
探究新知
引言
前面我们学习了直线的方程、圆的方程, 用直线的方程研究了两条直线的位置关系,本 节课我们类比用直线的方程研究两直线位置关 系的方法,运用直线与圆的方程,研究直线与 圆的的位置关系.
探究新知
探究一:用代数方式判断直线与圆的位置关系
探究新知
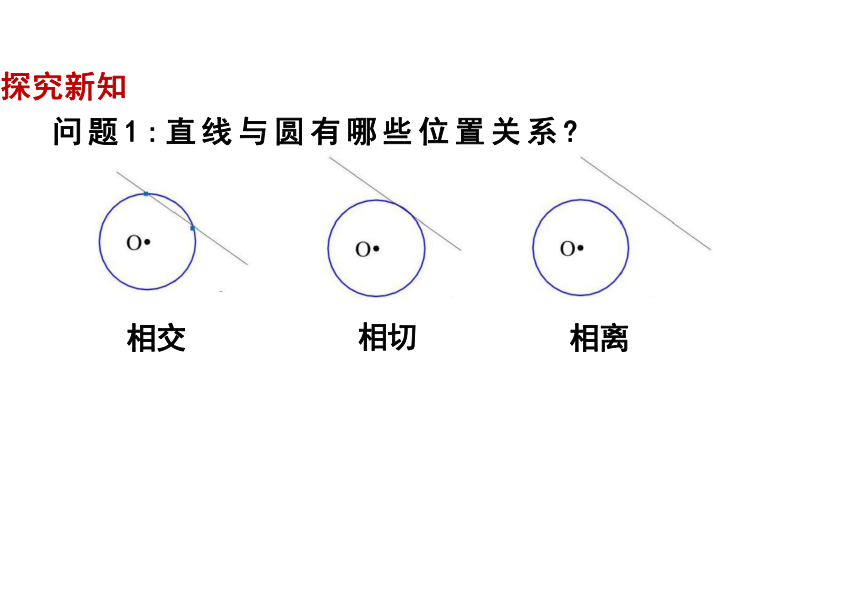
问题1:直线与圆有哪些位置关系
相交 相切 相离
探究新知
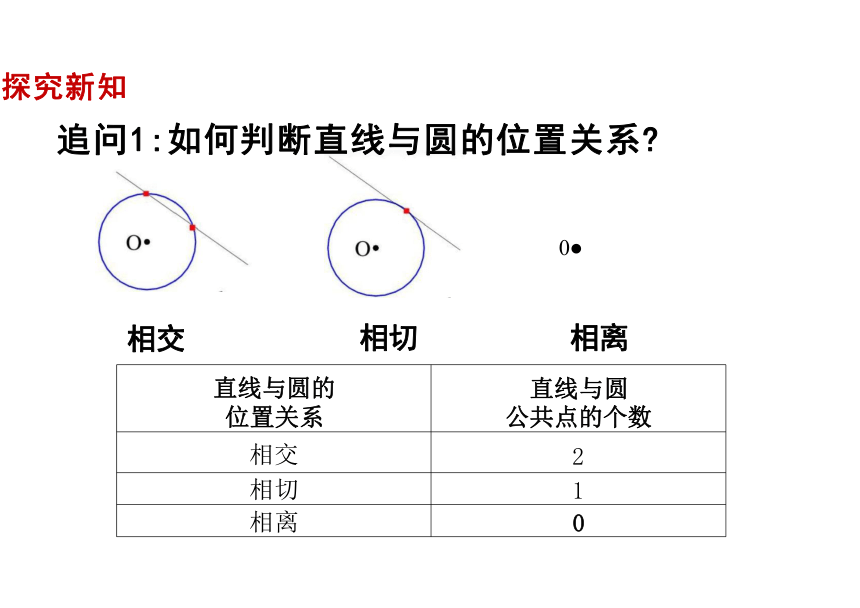
追问1:如何判断直线与圆的位置关系
0●
相交 相切 相离
直线与圆的 位置关系
直线与圆
公共点的个数
相交
2
相切
1
相离
0
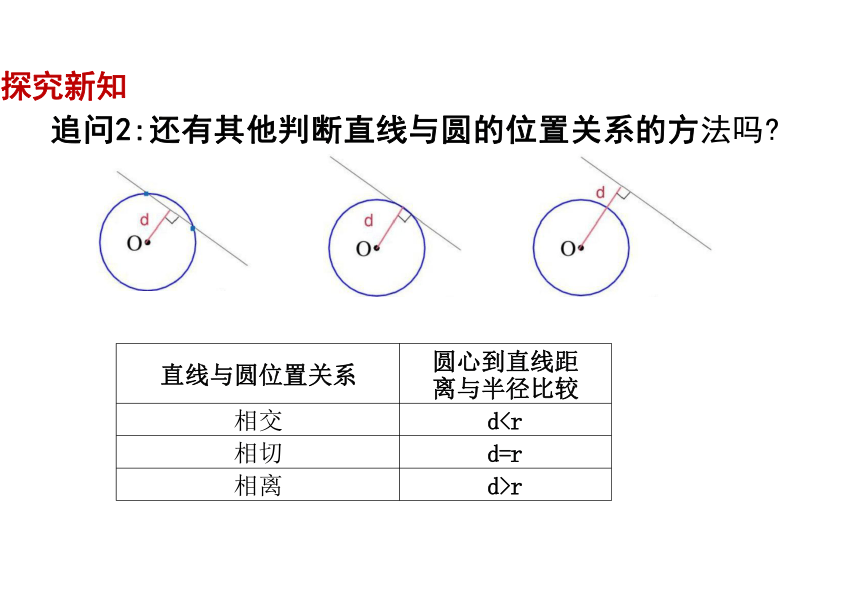
直线与圆位置关系
圆心到直线距 离与半径比较
相交
d相切
d=r
相离
d>r
探究新知
追问2:还有其他判断直线与圆的位置关系的方法吗
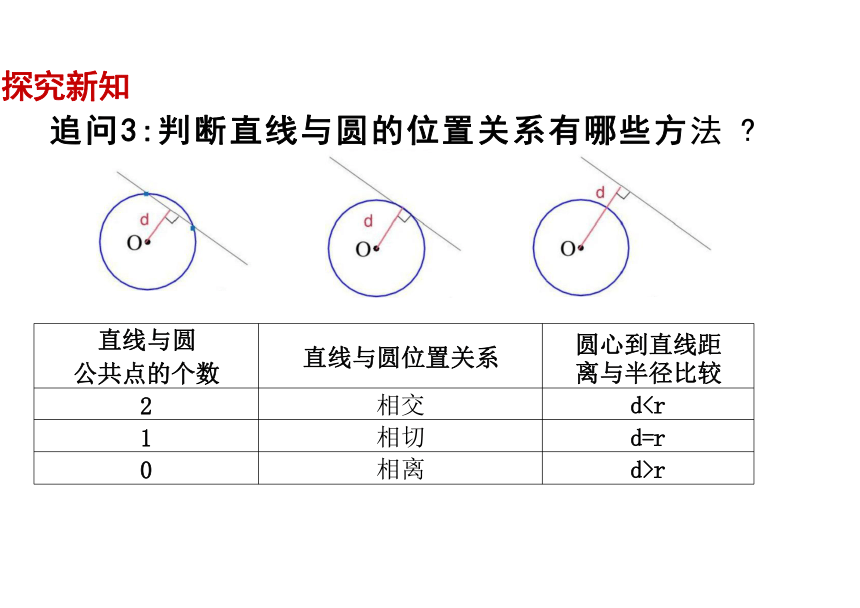
直线与圆 公共点的个数 直线与圆位置关系
圆心到直线距 离与半径比较
2 相交
d1 相切
d=r
0 相离
d>r
探究新知
追问3:判断直线与圆的位置关系有哪些方法
Ax+By+C=0
② +y +Dx+Ey+F=0
(D +E -4F>0)
代数方法 → 几何图形性质
探究新知
问题2:本章研究直线与圆的方法是什么
代数问题 — 几何问题
(x,y)
探究新知
追问:类比直线与直线的位置关系代数方法,以及根据上述定义
,如何利用直线和圆的方程判断它们之间的位置关系
两直线的位置关系— →联立两直线的方程
方程组的解的情况
l :3x+4y-2=0
l :2x+y+2=0
l 与l 的交点是M(- 2,2).
探究新知
追问:类比直线与直线的位置关系代数方法,以及根据上述定义
,如何利用直线和圆的方程判断它们之间的位置关系
两直线的位置关系— →联立两直线的方程
方程组解的情况
联立直线与 圆的方程
直线与圆的 位置关系
方程组解的情况
例题讲解
例1.已知直线l:3x+y-6=0 和圆心为C 的圆x +y -2y-4=0, 判
断直线l 与圆C的位置关系;如果相交,求直线l 被圆C所截得的弦长.
追问1:直线与圆的方程联立组成的方程组,如何判断解的个数
消去y, 得x -3x+2=0,
①
②
例题讲解
例1.已知直线l:3x+y-6=0 和圆心为C的圆x +y -2y-4=0, 判
断直线l与圆C的位置关系;如果相交,求直线l被圆C所截得的弦长.
△>0 → 方程有两组实数解← → 直线与圆相交 △=0< → 方程有一组实数解 → 直线与圆相切 △<0 → 方 程 没 有 实 数 解 直线与圆相离
例题讲解
例1.已知直线l:3x+y-6=0 和圆心为C的圆x +y -2y-4
C的位置关系;如果相交,求直线l被圆C所截得的弦长.
解法1:联立直线l 与圆C的方程,得
①
②
=0, 判断直线l与圆
代数法:联立方程
=3 .
所以,直线l与圆C相交,有两个公共点.
把x =2,x =1 分别代入方程①,得y =0,y
所以,直线l与 圆C的两个交点是A(2,0), B(1,3).
因此|AB| = √ (1-2) +(3-0) = √10.
消去y, 得x -3x+2=0,
由△>0,解得x =2,x =1.
探究新知
追问2:研究直线与圆的位置关系问题的基本思路是什么
思路1
几何————代数— →联立,解方程组—代数— —几何
位置关系 公共点的个数
几何———代数—→求d与r → 代数— —几何
位置关系 d 与r 的比较
追问3:还有其他方法判断直线与圆的位置关系吗
思路2
探究新知
例题讲解
例1.已知直线l:3x+y-6=0 和圆心为C的圆x +y -2y-4=0, 判
断直线与圆C的位置关系;如果相交,求直线l被圆C所截得的弦长.
解法2:圆C的方程x +y -2y-4=0 可化为
x +(y-1) =5,
因此圆心C的坐标为(0,1),半径为 √5, 圆心C(0,1) 到直线l的距离
探究新知
追问4:如何求圆心到直线的距离
点P(x ,y )到直线l:Axo+Byo+C=0 的距离
(其中A,B 不同时为0)
例题讲解
例1.已知直线l:3x+y-6=0 和圆心为C的圆x +y -2y-4=0, 判
断直线l与圆C的位置关系;如果相交,求直线l被圆C所截得的弦长.
解法2:圆C的方程x +y -2y -4=0 可化为
x +(y-1) =5,
因此圆心C的坐标为(0,1),半径为 √5, 圆心C(0,1) 到直线的距离
所以,直线l 与圆C相交,有两个公共点. 几何法:数形结合
如图,由垂径定理,得|AB|=2 √r2-d = √ 10.
法1:联立方程
△>0两组解 △=0一组解 △<0 无解
法2:比较d与r
dd=r
d>r
探究新知判断直线与圆的位置关系的方法
小结:
直线与圆相交
直线与圆相切 直线与圆相离
代数法是直接运用直线和圆的方程组成的方程组有无实数解 的情况判断直线与圆的位置关系,是完全代数的方法;具有程 序性、普适性.
几何法是利用图形中的相关几何量(圆心到直线的距离、圆 的半径)的大小判断直线与圆的位置关系,涉及圆心到直线距 离的计算。利用图形的几何性质,有助于简化计算.(数形结合
探究新知
代数法与几何法的比较:
探究新知
探究二:圆的切线方程
例题讲解
例2过点P(2,1) 作圆0:x +y =1 的切线l, 求切线l的方程.
追问1:过圆外一点作圆的切线,能作出几条
P(2,1)——→x +y =1
22+12>1
|PO|>1
追问1:过圆外一点作圆的切线,能作出几条
过圆外一点可以作圆的两条切线
追问2:如何刻画直线与圆相切
公共点的个数; 圆心到直线的距离
追问3:直线的方程选择什么形式
点斜式;两点式
例题讲解
例2过点P(2,1) 作圆0:x +y =1 的切线l, 求切线l的方程.
例题讲解
例2过点P(2,1)作圆0:x +y =1 的切线l,求切线l的方程
点斜式
解法2:几何法
解法1:代数法
例题讲解
例2过点P(2,1) 作圆0:x +y =1 的切线l, 求切线l的方程.
解法1 :设切线l的斜率为k, 则切线l 的方程为 y-1=k(x-2),
因为直线/与圆相切,所以方程组
只有一组解.
x=2
解法1:
消元,得(k +1)x +(2k-4k )x+4k -4k=0①.
因为方程①只有一个解,所以
△=4k (1-2k) -16k(k +1)(k-1)=0,
解得
所以,所求切线l的方程为y=1, 或4x-3y-5=0.
例题讲解
例2过点P(2,1) 作圆0:x +y =1 的切线l, 求切线l的方程.
例题讲解
例2过点P(2,1) 作圆0:x +y =1 的切线l, 求切线l的方程.
解法2:设切线l的斜率为k, 则切线l 的方程为 y-1=k(x-2), 即kx-y+1-2k=0.
由圆心(0,0)到切线l的距离等于圆的半径1,
因此,所求切线l的方程为y=1 或4x-3y-5=0.
,解得
得
例题讲解
例2过点P(2,1) 作圆0:x +y =1 的切线l, 求切线l 的方程.
联立方程,△=0 0A2PA
P(2,1)
A(xo,yo)
两点式
y
O
探究新知
追问4:你能比较这两种方法的差异吗
待定系数法求切线方方程方法
思路1 直线的方程
△=0
圆的方程
直线与圆相切
d=r
思路2
直线方程
课堂小结
问题3:这节课学习了哪些知识 用到了哪些方法呢
判断直线与圆的位置关系的方法:
定性描述
直线与圆的位置关系
定量表达
直线与圆公共点的个数
方程组实数解的个数
圆心到直线的距离
代数问题 直线与圆的位置关系 直线的方程 直线方程:Ax+By+C=0
圆的方程 圆心 (a,b), 半径r
实数解的个数
代数方法 →判断直线与圆的位置关系
课堂小结
问题3:这节课学习了哪些知识 用到了哪些方法呢
△=0 方程有一解 直线与圆相切,有一个交点
我们该如何去求切
线方程
联立方程
消去y后得到一个一元二次方程。
新知讲解
随堂检测
1.判断下列各组直线与圆C的位置关系:
(1)l:x-y+1=0, 圆C:x +y =3;
(2)l:3x+4y+2=0, 圆C:x +y -2x=0;
(3)l:x+y+3=0, 圆C:x +y +2y=0.
0),半径r=1, 圆心C(1,0) 到直线1:3x +4y+2=0 的距离 r,所以直线1:3x+4y+2=0 与 圆C:x + v -2x=0 相切.
-1),半径r=1, 圆心C(0,-1) 到直线
1:x+y+3=0 的距离
r, 所以直线l:x+y+3=0 与 圆C:x +y + 2y=0 相离 .
c(0,0), 半径r=√3, 圆心C(0,0) 到直
线l:x-y+1=0 的距离
,所以直线l:x-y+1=0 与圆C:
+v =3 相交.
解析 ( 1 ) 圆C:x +y =3 的圆心为 (2)圆C:x +y -2x=0 的圆心为C(1, (3)圆C:x +y +2y=0 的圆心为C(0,
合作探究 议、展、评
2. 已知直线4x+3y-35=0 与圆心在原点的圆C相切,求圆C 的
方程.
3.判断直线2x-y+2=0 与圆(x-1) +(y-2) =4 的位置关
系;如果相交,求直线被圆截得的弦长.
,解析 易知圆(x-1) +(y-2) =4的圆 心坐标为(1,2),半径r=2,
由点到直线的距离公式,得(1,2)到直
线 2x-y+2=0 的距离为
,所以直线2x-y+2=0 与圆
(x-1) +(y-2) =4相交.
所以弦长为
所以直线被圆截得的弦长
解析:设圆C的半径为r ,则 所以圆C 的方程为x +y =49.
习题讲解
直线与圆相交,有两个交点,可通过两 点坐标公式求弦长
直线与圆相切,有一个交点
直线与圆相离,无交点
小结
如何判断直线与圆的位置关系
代数法:
方程有两解
方程有一解
方程有0解
△>0
△=0 △<0
小结
如何判断直线与圆的位置关系
几何法:
dd=r, 直线与圆相切,有一个交点
d>r, 直线与圆相离,无交点
2.5.1直线与圆的位置关系
第一课时
素 养目 标
学 科 素 养
1.掌握直线与圆的三种位置关系:相交,相切, 相离;(重点) 2.会用代数法和几何法来判断直线与圆的三种位 置关系;(难点) 3.会用直线与圆的位置关系解决一些实际问 题. (重点、难点)
1、直观想象
2、数学运算
3、数形结合
学习目标
探究新知
引言
前面我们学习了直线的方程、圆的方程, 用直线的方程研究了两条直线的位置关系,本 节课我们类比用直线的方程研究两直线位置关 系的方法,运用直线与圆的方程,研究直线与 圆的的位置关系.
探究新知
探究一:用代数方式判断直线与圆的位置关系
探究新知
问题1:直线与圆有哪些位置关系
相交 相切 相离
探究新知
追问1:如何判断直线与圆的位置关系
0●
相交 相切 相离
直线与圆的 位置关系
直线与圆
公共点的个数
相交
2
相切
1
相离
0
直线与圆位置关系
圆心到直线距 离与半径比较
相交
d
d=r
相离
d>r
探究新知
追问2:还有其他判断直线与圆的位置关系的方法吗
直线与圆 公共点的个数 直线与圆位置关系
圆心到直线距 离与半径比较
2 相交
d
d=r
0 相离
d>r
探究新知
追问3:判断直线与圆的位置关系有哪些方法
Ax+By+C=0
② +y +Dx+Ey+F=0
(D +E -4F>0)
代数方法 → 几何图形性质
探究新知
问题2:本章研究直线与圆的方法是什么
代数问题 — 几何问题
(x,y)
探究新知
追问:类比直线与直线的位置关系代数方法,以及根据上述定义
,如何利用直线和圆的方程判断它们之间的位置关系
两直线的位置关系— →联立两直线的方程
方程组的解的情况
l :3x+4y-2=0
l :2x+y+2=0
l 与l 的交点是M(- 2,2).
探究新知
追问:类比直线与直线的位置关系代数方法,以及根据上述定义
,如何利用直线和圆的方程判断它们之间的位置关系
两直线的位置关系— →联立两直线的方程
方程组解的情况
联立直线与 圆的方程
直线与圆的 位置关系
方程组解的情况
例题讲解
例1.已知直线l:3x+y-6=0 和圆心为C 的圆x +y -2y-4=0, 判
断直线l 与圆C的位置关系;如果相交,求直线l 被圆C所截得的弦长.
追问1:直线与圆的方程联立组成的方程组,如何判断解的个数
消去y, 得x -3x+2=0,
①
②
例题讲解
例1.已知直线l:3x+y-6=0 和圆心为C的圆x +y -2y-4=0, 判
断直线l与圆C的位置关系;如果相交,求直线l被圆C所截得的弦长.
△>0 → 方程有两组实数解← → 直线与圆相交 △=0< → 方程有一组实数解 → 直线与圆相切 △<0 → 方 程 没 有 实 数 解 直线与圆相离
例题讲解
例1.已知直线l:3x+y-6=0 和圆心为C的圆x +y -2y-4
C的位置关系;如果相交,求直线l被圆C所截得的弦长.
解法1:联立直线l 与圆C的方程,得
①
②
=0, 判断直线l与圆
代数法:联立方程
=3 .
所以,直线l与圆C相交,有两个公共点.
把x =2,x =1 分别代入方程①,得y =0,y
所以,直线l与 圆C的两个交点是A(2,0), B(1,3).
因此|AB| = √ (1-2) +(3-0) = √10.
消去y, 得x -3x+2=0,
由△>0,解得x =2,x =1.
探究新知
追问2:研究直线与圆的位置关系问题的基本思路是什么
思路1
几何————代数— →联立,解方程组—代数— —几何
位置关系 公共点的个数
几何———代数—→求d与r → 代数— —几何
位置关系 d 与r 的比较
追问3:还有其他方法判断直线与圆的位置关系吗
思路2
探究新知
例题讲解
例1.已知直线l:3x+y-6=0 和圆心为C的圆x +y -2y-4=0, 判
断直线与圆C的位置关系;如果相交,求直线l被圆C所截得的弦长.
解法2:圆C的方程x +y -2y-4=0 可化为
x +(y-1) =5,
因此圆心C的坐标为(0,1),半径为 √5, 圆心C(0,1) 到直线l的距离
探究新知
追问4:如何求圆心到直线的距离
点P(x ,y )到直线l:Axo+Byo+C=0 的距离
(其中A,B 不同时为0)
例题讲解
例1.已知直线l:3x+y-6=0 和圆心为C的圆x +y -2y-4=0, 判
断直线l与圆C的位置关系;如果相交,求直线l被圆C所截得的弦长.
解法2:圆C的方程x +y -2y -4=0 可化为
x +(y-1) =5,
因此圆心C的坐标为(0,1),半径为 √5, 圆心C(0,1) 到直线的距离
所以,直线l 与圆C相交,有两个公共点. 几何法:数形结合
如图,由垂径定理,得|AB|=2 √r2-d = √ 10.
法1:联立方程
△>0两组解 △=0一组解 △<0 无解
法2:比较d与r
d
d>r
探究新知判断直线与圆的位置关系的方法
小结:
直线与圆相交
直线与圆相切 直线与圆相离
代数法是直接运用直线和圆的方程组成的方程组有无实数解 的情况判断直线与圆的位置关系,是完全代数的方法;具有程 序性、普适性.
几何法是利用图形中的相关几何量(圆心到直线的距离、圆 的半径)的大小判断直线与圆的位置关系,涉及圆心到直线距 离的计算。利用图形的几何性质,有助于简化计算.(数形结合
探究新知
代数法与几何法的比较:
探究新知
探究二:圆的切线方程
例题讲解
例2过点P(2,1) 作圆0:x +y =1 的切线l, 求切线l的方程.
追问1:过圆外一点作圆的切线,能作出几条
P(2,1)——→x +y =1
22+12>1
|PO|>1
追问1:过圆外一点作圆的切线,能作出几条
过圆外一点可以作圆的两条切线
追问2:如何刻画直线与圆相切
公共点的个数; 圆心到直线的距离
追问3:直线的方程选择什么形式
点斜式;两点式
例题讲解
例2过点P(2,1) 作圆0:x +y =1 的切线l, 求切线l的方程.
例题讲解
例2过点P(2,1)作圆0:x +y =1 的切线l,求切线l的方程
点斜式
解法2:几何法
解法1:代数法
例题讲解
例2过点P(2,1) 作圆0:x +y =1 的切线l, 求切线l的方程.
解法1 :设切线l的斜率为k, 则切线l 的方程为 y-1=k(x-2),
因为直线/与圆相切,所以方程组
只有一组解.
x=2
解法1:
消元,得(k +1)x +(2k-4k )x+4k -4k=0①.
因为方程①只有一个解,所以
△=4k (1-2k) -16k(k +1)(k-1)=0,
解得
所以,所求切线l的方程为y=1, 或4x-3y-5=0.
例题讲解
例2过点P(2,1) 作圆0:x +y =1 的切线l, 求切线l的方程.
例题讲解
例2过点P(2,1) 作圆0:x +y =1 的切线l, 求切线l的方程.
解法2:设切线l的斜率为k, 则切线l 的方程为 y-1=k(x-2), 即kx-y+1-2k=0.
由圆心(0,0)到切线l的距离等于圆的半径1,
因此,所求切线l的方程为y=1 或4x-3y-5=0.
,解得
得
例题讲解
例2过点P(2,1) 作圆0:x +y =1 的切线l, 求切线l 的方程.
联立方程,△=0 0A2PA
P(2,1)
A(xo,yo)
两点式
y
O
探究新知
追问4:你能比较这两种方法的差异吗
待定系数法求切线方方程方法
思路1 直线的方程
△=0
圆的方程
直线与圆相切
d=r
思路2
直线方程
课堂小结
问题3:这节课学习了哪些知识 用到了哪些方法呢
判断直线与圆的位置关系的方法:
定性描述
直线与圆的位置关系
定量表达
直线与圆公共点的个数
方程组实数解的个数
圆心到直线的距离
代数问题 直线与圆的位置关系 直线的方程 直线方程:Ax+By+C=0
圆的方程 圆心 (a,b), 半径r
实数解的个数
代数方法 →判断直线与圆的位置关系
课堂小结
问题3:这节课学习了哪些知识 用到了哪些方法呢
△=0 方程有一解 直线与圆相切,有一个交点
我们该如何去求切
线方程
联立方程
消去y后得到一个一元二次方程。
新知讲解
随堂检测
1.判断下列各组直线与圆C的位置关系:
(1)l:x-y+1=0, 圆C:x +y =3;
(2)l:3x+4y+2=0, 圆C:x +y -2x=0;
(3)l:x+y+3=0, 圆C:x +y +2y=0.
0),半径r=1, 圆心C(1,0) 到直线1:3x +4y+2=0 的距离 r,所以直线1:3x+4y+2=0 与 圆C:x + v -2x=0 相切.
-1),半径r=1, 圆心C(0,-1) 到直线
1:x+y+3=0 的距离
r, 所以直线l:x+y+3=0 与 圆C:x +y + 2y=0 相离 .
c(0,0), 半径r=√3, 圆心C(0,0) 到直
线l:x-y+1=0 的距离
,所以直线l:x-y+1=0 与圆C:
+v =3 相交.
解析 ( 1 ) 圆C:x +y =3 的圆心为 (2)圆C:x +y -2x=0 的圆心为C(1, (3)圆C:x +y +2y=0 的圆心为C(0,
合作探究 议、展、评
2. 已知直线4x+3y-35=0 与圆心在原点的圆C相切,求圆C 的
方程.
3.判断直线2x-y+2=0 与圆(x-1) +(y-2) =4 的位置关
系;如果相交,求直线被圆截得的弦长.
,解析 易知圆(x-1) +(y-2) =4的圆 心坐标为(1,2),半径r=2,
由点到直线的距离公式,得(1,2)到直
线 2x-y+2=0 的距离为
,所以直线2x-y+2=0 与圆
(x-1) +(y-2) =4相交.
所以弦长为
所以直线被圆截得的弦长
解析:设圆C的半径为r ,则 所以圆C 的方程为x +y =49.
习题讲解
直线与圆相交,有两个交点,可通过两 点坐标公式求弦长
直线与圆相切,有一个交点
直线与圆相离,无交点
小结
如何判断直线与圆的位置关系
代数法:
方程有两解
方程有一解
方程有0解
△>0
△=0 △<0
小结
如何判断直线与圆的位置关系
几何法:
d
d>r, 直线与圆相离,无交点
