3.1.1 椭圆及其标准方程-课件(共33张PPT)-高中数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 3.1.1 椭圆及其标准方程-课件(共33张PPT)-高中数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 22:25:54 | ||
图片预览









文档简介
(共33张PPT)
3.1.1椭圆及其标准方程
探究:取一条定长的细绳,把它的两端都固定在图板的同一点,套
上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个 圆.如果把细绳的两端拉开一段距离,分别固定在图板的两点F ,
F (如图),套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲
线 在这一过程中,移动的笔尖(动点)满足的几何条件是什么
椭圆是圆锥曲线的一种,具有丰富的几何性质,在科研、生产和人类生活
中具有广泛的应用.那么,椭圆到底有怎样的几何特征 我们该如何利用这些特
征建立椭圆的方程,从而为研究椭圆的几何性质奠定基础
实验引入
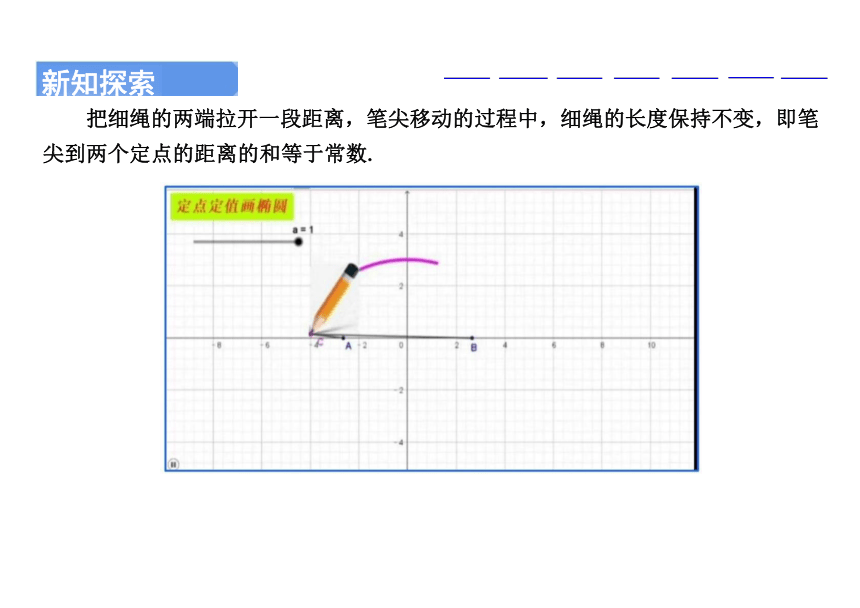
把细绳的两端拉开一段距离,笔尖移动的过程中,细绳的长度保持不变,即笔
尖到两个定点的距离的和等于常数.
新知探索
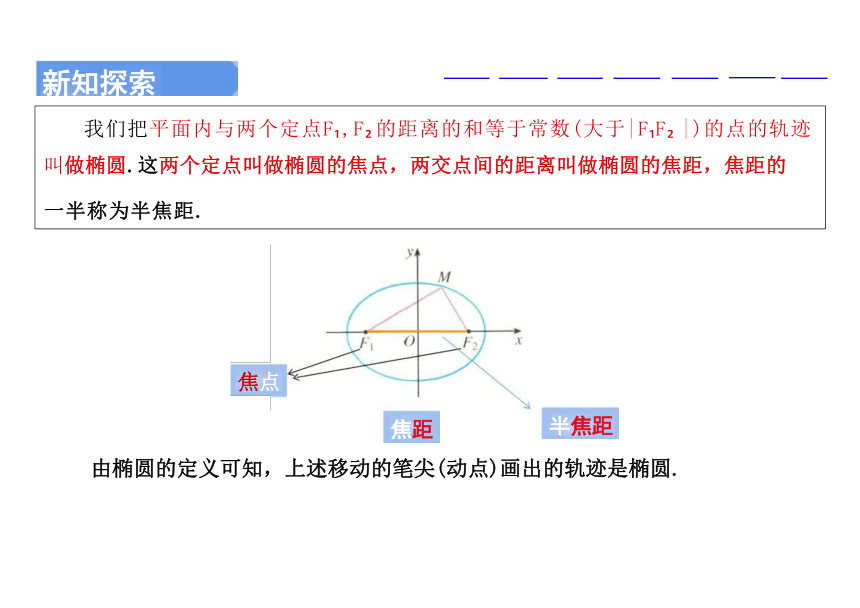
我们把平面内与两个定点F ,F 的距离的和等于常数(大于|F F |)的点的轨迹
叫做椭圆.这两个定点叫做椭圆的焦点,两交点间的距离叫做椭圆的焦距,焦距的
一半称为半焦距.
焦点
由椭圆的定义可知,上述移动的笔尖(动点)画出的轨迹是椭圆.
新知探索
半焦距
焦距
观察我们画出的图形,可以发现椭圆具有对称性,而且过两
个焦点的直线是它的对称轴,所以我们以经过椭圆两焦点F , F 的直线为x轴,线段F F 的垂直平分线为y轴,建立平面直 角坐标系0xy, 如图所示.
下面我们根据椭圆的几何特征,选择适当的坐标系,建立椭圆的方程.
思考1:观察椭圆的形状,你认为怎样建立平面直角坐标系可能使所得的椭圆方
程形式简单
新知探索
P={M||MF |+|MF |=2a}.
因为|MF I= √ (x+c) +y2,|MF I= √ (x-c) +y2,
所以 √(x+c) +y + √ (x-c) +y =2a.
设M(x,y) 是椭圆上任意一点,椭圆的焦距为2c(c>0), 那么焦点F ,F 的
坐标分别为(一,0),(c,0). 根据椭圆的定义,设点M与焦点F ,F 的距离的和等于
2a.
由椭圆的定义可知,椭圆可看作点集
新知探索
①
为了简化方程①,我们将其左边的一个根式移到右边,得
√(x+c) +y =2a-√(x-c) +y2. ②
对方程②两边平方,得(x+c) +y =4a -4a √ (x-c) +y +(x-c) +y .
整理,得a -cx=a√(x-c) +y2. ③
对方程③两边平方,得a -2a cx+c x =a x -2a cx+a c +a y .
整理,得(a -c )x +a y =a (a -c ). ④
将方程④两边同时除以a (a -c ), ⑤
由椭圆的定义可知,2a>2c>0, 即a>c>0, 所 以(a -c )>0.
新知探索
由于方程②③的两边都是非负实数,因此方程到方程的变形都是同解变形.这样,
椭圆上任意一点(x,y) 的坐标都满足方程⑥;反之,以方程⑥的解为坐标的点
(x,y)与椭圆的两个焦点(c,0), (一,0)的距离之和为2a, 即以方程⑥的解为坐标的
点都在椭圆上.我们称方程⑥是椭圆的方程,这个方程叫做椭圆的标准方程.它表 示焦点在x轴上,两个焦点分别是F (c,0),F (-c,0) 的椭圆,这里c =a +b .
思考2:观察图,你能从中找出表示a,c,√a -c 的线段吗
由图知, |PF I=|PF I=a,|OF I=|0F I=c,|PO|= √a -c .
令b=|PO|=√a -c2, 那么方程⑤就
新知探索
思考3:如图,如果焦点F ,F 在y轴上,且F ,F 的坐标分别 为(0,一),(0,c),a,b 的意义同上,那么椭圆的方程是什么
容易知道,此时椭圆的方程
程也是椭圆的方程.
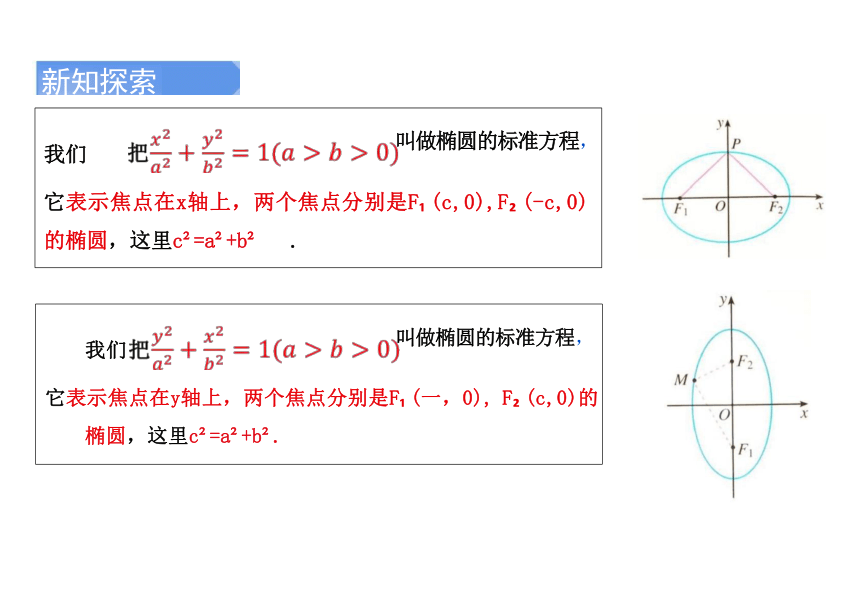
我们把 叫做椭圆的标准方程,它表示焦点在x轴上
两个焦点分别是F (c,0),F (-c,0)的椭圆,这里c =a +b .
新知探索
我们
叫做椭圆的标准方程,
它表示焦点在y轴上,两个焦点分别是F (一,0), F (c,0)的 椭圆,这里c =a +b .
我们
叫做椭圆的标准方程,
它表示焦点在x轴上,两个焦点分别是F (c,0),F (-c,0) 的椭圆,这里c =a +b .
新知探索
辨析1.判断正误.
(1)到平面内两个定点的距离之和等于定长的轨迹叫做椭圆.()
(2)到两定点F (-2,0) 和F (2,0)的距离之和为3的点的轨迹为椭圆.()
答案:×,×.
辨析2.设P是椭圆 上的任意一点,若F ,F 是椭圆的两个焦点,则
|PF I+|PF | 等于( ).
A.10 B.8 C.5 D.4
答案:A.
新知探索
所以a=√ 10.
所以b =a -c =10-4=6.
所以,所求椭圆的标准方程
准方程.
解:由于椭圆的焦点在轴上,所以设它的标准方程
例1.已知椭圆的两个焦点坐标分别是(2,0),(-2,0),并且经过点 求它的标
例析
例2.如图,在圆x +y =4 上任意取一点P, 过点P作x轴的垂线段 PD,D 为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是什
么 为什么 (当点P经过圆与x轴的交点时,规定点M 与点P重合.)
解:设点M 的坐标为(x,y),点 P的坐标为(x ,yo),则 点D的坐
标为(x ,0).由点M 是线段PD 的中点,得x =xo,
因为点P(x ,yo)在圆x +y =4 上,所以xo +yo =4.①
把x=xo,yo=2y 代入方程①,得x +4y =4,
所以点M 的轨迹是椭圆.
例析
即
。
思考4:由例2我们发现,可以由圆通过“压缩”得到椭圆.你能通过“拉伸”得到
椭圆吗 如何“拉伸” 由此你能发现椭圆与圆之间的关系吗
从例2我们可以发现,将圆x +y =4 上的所有点的横坐标保持不变,纵坐标变为
原来的 时,利用三角函数中学习的伸缩变换的知识,可以得到x +(2y) =4, 即 ,此为椭圆方程.同理可将圆上所有点的横坐标保持不变,纵坐标变为 原来的2倍,利用伸缩变换可得 得到拉伸后的椭圆 方程.所以椭圆可以由圆经过伸缩变换得到.
新知探索
例3.如图,在A,B 两点的坐标分别为(-5,0),(5,0).直线AM,BM
相交于点M, 且它们的斜率之积是 求点M的轨迹方程.
解:设点M 的坐标为(x,y),因为点A的坐标为(-5,0),
所以直线AM的斜率为 .同理,直线BM 的斜率为
由已知,
化简,得点M的轨迹方程
点M 的轨迹是除去(-5,0),(5,0)两点的椭圆.
例析
到两点F ,F 的距离之和大于8的点的轨迹是椭圆
到两点F ,F 的距离之和等于6的点的轨迹是椭圆
的距离之和等于从点(5,3)到F ,F 的距离之和的点的轨迹
D.到点F (-4,0),F (4,0) 距离相等的点的轨迹是椭圆
答案:D.
A.已知F (-4,0),F (4,0),
B.已知F (-4,0),F (4,0), C.到点F (-4,0),F (4,0) 是椭圆
题型一:椭圆的定义及应用
例1.(1)下列说法正确的的是().
题型一:椭圆的定义及应用_
例1.(2)若椭 上一点P到一个焦点的距离为5,则P到另一个焦点的距离
为
答案:5.
解:由椭圆方 知a=5, 设椭圆的两个焦点分别为F ,F ,
令|PF I=5, 由椭圆的定义知|PF I+|PF I=2a=10,
所以|PF I=10-5=5.
练习
椭圆定义的双向应用
1.判断:符合定义中到两定点的距离之和为常数(大于两定点的距离)这一条件的
点的轨迹为椭圆.
2.求值:椭圆上的点一定满足定义中的条件,即到两定点的距离之和为2.
练习
方法技巧:
解:如图,∵|AF I+|AF I=2a,|BF I+|BF |=2a,
∴C△ABF =|AB|+|BF I+|AF I
=|AF I+|BF |+|AF |+|BF |=4a.
,F ,F 是它的焦点.过F 的直线与椭圆交于A,
变1.已知椭
B两点,求△ABF 的周长.
练习
题型二: _定义法求椭圆标准方程__
例2.已知圆A:(x+3) +y =100, 圆A内一定点B(3,0), 圆
过B且与圆A内切,求圆心P的轨迹方程.
解:设圆P的半径为r,∵ 圆P过点B,∴|PB|=r.
又∵圆P与圆A内切,圆A的半径为10,
∴两圆的圆心距|PA|=10-r, 即 |PA|+|PB|=10 (大于 A|B|)
∴点P的轨迹是以A,B 为焦点的椭圆.
∴2a=10,2c=|AB|=6,∴a=5,c=3.∴b =a -c =16.
即点的轨迹方程
练习
题型二: _定义法求椭圆标准方程
例2.已知圆A:(x+3) +y =100, 圆A内一定点B(3,0),圆
过B且与圆A内切,求圆心的轨迹方程。
∴2a=10,2c=|AB|=6,∴a=5,c=3.∴b =a -c =16.
即点的轨迹方程
练习
练习
方法技巧:
定义法求椭圆的标准方程
1.先根据动点具有的条件,验证是否符合椭圆的定义,即动点到两定点距离之和
是否是一常数,且该常数(定值)大于两定点间的距离.
2.若符合,则动点的轨迹为椭圆,且两定点间的距离为焦距2,动点到两定点的距
离之和为2a, 从而可以确定椭圆的方程.
变2.如图,已知圆(x+1) +y =16 及点A(1,0),Q 为圆上一点. AQ 的垂直平分线交CQ 于M, 求 点M 的轨迹方程.
解:由垂直平分线性质可知MQI=|MA|,
∴|CM|+|MA|=|CM|+|MQ|=|CQ|.
∴|CM|+|MA|=4.
又∵|AC|=2, 所 以M点轨迹为椭圆。
由椭圆定义知a=2,c=1,∴b =a -c =3.
∴所求轨迹方程
练习
题型三:待定系数法求椭圆标准方程
例3.求适合下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别为(-4,0)和(4,0),且椭圆经过点(5,0); (2)焦点在y轴上,且经过两个点(0,2)和(1,0);
解(1).由于椭圆的焦点在x轴上,∴设它的标准方程
∴a=5,c=4,∴b =a -c2=25-16=9.
故所求椭圆的标准方程
解(2).由于椭圆的焦点在y轴上,∴设它的标准方程
∴a=2,b=1,
故所求椭圆的标准方程
练习
例3.求适合下列条件的椭圆的标准方程:
(3)经过点A(√3,-2) 和点B(-2√3,1).
解(3):法一(分类讨论法)
①当焦点在x轴上时,设椭圆的标准方程
依题意有 解
故所求椭圆的标准方程
练习
②当焦点在y轴上时,设椭圆的标准方程
依题意 解
∵a>b>0,∴ 无 解 .
例3.求适合下列条件的椭圆的标准方程: (3)经过点A(√3,-2) 和点B(-2√3,1).
解(3):法一(分类讨论法)
练习
设所求椭圆的方程为mx +ny =1((m≠n,m>0,n>0).
依题意 解
故所求椭圆的标准方程
例3.求适合下列条件的椭圆的标准方程: (3)经过点A(√3,-2) 和点B(-2√3,1).
解(3):法二(待定系数法)
练习
方法技巧:
1.利用待定系数法求椭圆标准方程的步骤:
(1)先确定焦点位置;(2)设出方程;(3)寻求a,b,c 的等量关系;(4)求出a,b 的
值,代入所设方程.
2. 当焦点位置不确定时,可设椭圆方程为mx +ny =1(m≠ n,m>0,n>0).
因为它包括焦点在x 轴上(mn) 两类情况,所以可以避免
分类讨论,从而简化了运算.
变3.求适合下列条件的椭圆的标准方程: (1)经过两点(2,- √2),
解(1):(待定系数法)
设所求椭圆的方程为mx +ny =1((m≠n,
依题意有
故所求椭圆的标准方程
练习
m> 0 ,n>0).
解
变3.求适合下列条件的椭圆的标准方程:
(2)过点( √3,- √5),且与椭 有相同的焦点.
解:∵所求椭圆与椭 有相同的焦点,
∴其焦点在y轴上,且c =25-9=16. 设它的标准方程
∵c =16, 且c =a -b , 故a -b =16.①
又∵点( √3,- √5)在椭圆上, , 即 .②
由①②得b =4,a =20,
所以所求椭圆的标准方程
练习
··
1.椭圆的定义:把平面内与两个定点F ,F 的距离的和等于常数(大于|F F I) 的 点
的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两交点间的距离叫做椭圆的焦距,
焦距的一半称为半焦距.
课堂小结
焦点在x轴上 焦点在y轴上
标准方程 +能=1(a>b>0) +=1(a>b>0)
图形
焦点 (一,0),(c,0) (0,-c),(0,c)
a,b,c 的 关 系 c =a -b
课堂小结
2.椭圆的标准方程:
(1)整理本节课的题型;
(2)课本P109的练习1——4题;
(3)课本P115习题3.1第3、2题。
作业
3.1.1椭圆及其标准方程
探究:取一条定长的细绳,把它的两端都固定在图板的同一点,套
上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个 圆.如果把细绳的两端拉开一段距离,分别固定在图板的两点F ,
F (如图),套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲
线 在这一过程中,移动的笔尖(动点)满足的几何条件是什么
椭圆是圆锥曲线的一种,具有丰富的几何性质,在科研、生产和人类生活
中具有广泛的应用.那么,椭圆到底有怎样的几何特征 我们该如何利用这些特
征建立椭圆的方程,从而为研究椭圆的几何性质奠定基础
实验引入
把细绳的两端拉开一段距离,笔尖移动的过程中,细绳的长度保持不变,即笔
尖到两个定点的距离的和等于常数.
新知探索
我们把平面内与两个定点F ,F 的距离的和等于常数(大于|F F |)的点的轨迹
叫做椭圆.这两个定点叫做椭圆的焦点,两交点间的距离叫做椭圆的焦距,焦距的
一半称为半焦距.
焦点
由椭圆的定义可知,上述移动的笔尖(动点)画出的轨迹是椭圆.
新知探索
半焦距
焦距
观察我们画出的图形,可以发现椭圆具有对称性,而且过两
个焦点的直线是它的对称轴,所以我们以经过椭圆两焦点F , F 的直线为x轴,线段F F 的垂直平分线为y轴,建立平面直 角坐标系0xy, 如图所示.
下面我们根据椭圆的几何特征,选择适当的坐标系,建立椭圆的方程.
思考1:观察椭圆的形状,你认为怎样建立平面直角坐标系可能使所得的椭圆方
程形式简单
新知探索
P={M||MF |+|MF |=2a}.
因为|MF I= √ (x+c) +y2,|MF I= √ (x-c) +y2,
所以 √(x+c) +y + √ (x-c) +y =2a.
设M(x,y) 是椭圆上任意一点,椭圆的焦距为2c(c>0), 那么焦点F ,F 的
坐标分别为(一,0),(c,0). 根据椭圆的定义,设点M与焦点F ,F 的距离的和等于
2a.
由椭圆的定义可知,椭圆可看作点集
新知探索
①
为了简化方程①,我们将其左边的一个根式移到右边,得
√(x+c) +y =2a-√(x-c) +y2. ②
对方程②两边平方,得(x+c) +y =4a -4a √ (x-c) +y +(x-c) +y .
整理,得a -cx=a√(x-c) +y2. ③
对方程③两边平方,得a -2a cx+c x =a x -2a cx+a c +a y .
整理,得(a -c )x +a y =a (a -c ). ④
将方程④两边同时除以a (a -c ), ⑤
由椭圆的定义可知,2a>2c>0, 即a>c>0, 所 以(a -c )>0.
新知探索
由于方程②③的两边都是非负实数,因此方程到方程的变形都是同解变形.这样,
椭圆上任意一点(x,y) 的坐标都满足方程⑥;反之,以方程⑥的解为坐标的点
(x,y)与椭圆的两个焦点(c,0), (一,0)的距离之和为2a, 即以方程⑥的解为坐标的
点都在椭圆上.我们称方程⑥是椭圆的方程,这个方程叫做椭圆的标准方程.它表 示焦点在x轴上,两个焦点分别是F (c,0),F (-c,0) 的椭圆,这里c =a +b .
思考2:观察图,你能从中找出表示a,c,√a -c 的线段吗
由图知, |PF I=|PF I=a,|OF I=|0F I=c,|PO|= √a -c .
令b=|PO|=√a -c2, 那么方程⑤就
新知探索
思考3:如图,如果焦点F ,F 在y轴上,且F ,F 的坐标分别 为(0,一),(0,c),a,b 的意义同上,那么椭圆的方程是什么
容易知道,此时椭圆的方程
程也是椭圆的方程.
我们把 叫做椭圆的标准方程,它表示焦点在x轴上
两个焦点分别是F (c,0),F (-c,0)的椭圆,这里c =a +b .
新知探索
我们
叫做椭圆的标准方程,
它表示焦点在y轴上,两个焦点分别是F (一,0), F (c,0)的 椭圆,这里c =a +b .
我们
叫做椭圆的标准方程,
它表示焦点在x轴上,两个焦点分别是F (c,0),F (-c,0) 的椭圆,这里c =a +b .
新知探索
辨析1.判断正误.
(1)到平面内两个定点的距离之和等于定长的轨迹叫做椭圆.()
(2)到两定点F (-2,0) 和F (2,0)的距离之和为3的点的轨迹为椭圆.()
答案:×,×.
辨析2.设P是椭圆 上的任意一点,若F ,F 是椭圆的两个焦点,则
|PF I+|PF | 等于( ).
A.10 B.8 C.5 D.4
答案:A.
新知探索
所以a=√ 10.
所以b =a -c =10-4=6.
所以,所求椭圆的标准方程
准方程.
解:由于椭圆的焦点在轴上,所以设它的标准方程
例1.已知椭圆的两个焦点坐标分别是(2,0),(-2,0),并且经过点 求它的标
例析
例2.如图,在圆x +y =4 上任意取一点P, 过点P作x轴的垂线段 PD,D 为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是什
么 为什么 (当点P经过圆与x轴的交点时,规定点M 与点P重合.)
解:设点M 的坐标为(x,y),点 P的坐标为(x ,yo),则 点D的坐
标为(x ,0).由点M 是线段PD 的中点,得x =xo,
因为点P(x ,yo)在圆x +y =4 上,所以xo +yo =4.①
把x=xo,yo=2y 代入方程①,得x +4y =4,
所以点M 的轨迹是椭圆.
例析
即
。
思考4:由例2我们发现,可以由圆通过“压缩”得到椭圆.你能通过“拉伸”得到
椭圆吗 如何“拉伸” 由此你能发现椭圆与圆之间的关系吗
从例2我们可以发现,将圆x +y =4 上的所有点的横坐标保持不变,纵坐标变为
原来的 时,利用三角函数中学习的伸缩变换的知识,可以得到x +(2y) =4, 即 ,此为椭圆方程.同理可将圆上所有点的横坐标保持不变,纵坐标变为 原来的2倍,利用伸缩变换可得 得到拉伸后的椭圆 方程.所以椭圆可以由圆经过伸缩变换得到.
新知探索
例3.如图,在A,B 两点的坐标分别为(-5,0),(5,0).直线AM,BM
相交于点M, 且它们的斜率之积是 求点M的轨迹方程.
解:设点M 的坐标为(x,y),因为点A的坐标为(-5,0),
所以直线AM的斜率为 .同理,直线BM 的斜率为
由已知,
化简,得点M的轨迹方程
点M 的轨迹是除去(-5,0),(5,0)两点的椭圆.
例析
到两点F ,F 的距离之和大于8的点的轨迹是椭圆
到两点F ,F 的距离之和等于6的点的轨迹是椭圆
的距离之和等于从点(5,3)到F ,F 的距离之和的点的轨迹
D.到点F (-4,0),F (4,0) 距离相等的点的轨迹是椭圆
答案:D.
A.已知F (-4,0),F (4,0),
B.已知F (-4,0),F (4,0), C.到点F (-4,0),F (4,0) 是椭圆
题型一:椭圆的定义及应用
例1.(1)下列说法正确的的是().
题型一:椭圆的定义及应用_
例1.(2)若椭 上一点P到一个焦点的距离为5,则P到另一个焦点的距离
为
答案:5.
解:由椭圆方 知a=5, 设椭圆的两个焦点分别为F ,F ,
令|PF I=5, 由椭圆的定义知|PF I+|PF I=2a=10,
所以|PF I=10-5=5.
练习
椭圆定义的双向应用
1.判断:符合定义中到两定点的距离之和为常数(大于两定点的距离)这一条件的
点的轨迹为椭圆.
2.求值:椭圆上的点一定满足定义中的条件,即到两定点的距离之和为2.
练习
方法技巧:
解:如图,∵|AF I+|AF I=2a,|BF I+|BF |=2a,
∴C△ABF =|AB|+|BF I+|AF I
=|AF I+|BF |+|AF |+|BF |=4a.
,F ,F 是它的焦点.过F 的直线与椭圆交于A,
变1.已知椭
B两点,求△ABF 的周长.
练习
题型二: _定义法求椭圆标准方程__
例2.已知圆A:(x+3) +y =100, 圆A内一定点B(3,0), 圆
过B且与圆A内切,求圆心P的轨迹方程.
解:设圆P的半径为r,∵ 圆P过点B,∴|PB|=r.
又∵圆P与圆A内切,圆A的半径为10,
∴两圆的圆心距|PA|=10-r, 即 |PA|+|PB|=10 (大于 A|B|)
∴点P的轨迹是以A,B 为焦点的椭圆.
∴2a=10,2c=|AB|=6,∴a=5,c=3.∴b =a -c =16.
即点的轨迹方程
练习
题型二: _定义法求椭圆标准方程
例2.已知圆A:(x+3) +y =100, 圆A内一定点B(3,0),圆
过B且与圆A内切,求圆心的轨迹方程。
∴2a=10,2c=|AB|=6,∴a=5,c=3.∴b =a -c =16.
即点的轨迹方程
练习
练习
方法技巧:
定义法求椭圆的标准方程
1.先根据动点具有的条件,验证是否符合椭圆的定义,即动点到两定点距离之和
是否是一常数,且该常数(定值)大于两定点间的距离.
2.若符合,则动点的轨迹为椭圆,且两定点间的距离为焦距2,动点到两定点的距
离之和为2a, 从而可以确定椭圆的方程.
变2.如图,已知圆(x+1) +y =16 及点A(1,0),Q 为圆上一点. AQ 的垂直平分线交CQ 于M, 求 点M 的轨迹方程.
解:由垂直平分线性质可知MQI=|MA|,
∴|CM|+|MA|=|CM|+|MQ|=|CQ|.
∴|CM|+|MA|=4.
又∵|AC|=2, 所 以M点轨迹为椭圆。
由椭圆定义知a=2,c=1,∴b =a -c =3.
∴所求轨迹方程
练习
题型三:待定系数法求椭圆标准方程
例3.求适合下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别为(-4,0)和(4,0),且椭圆经过点(5,0); (2)焦点在y轴上,且经过两个点(0,2)和(1,0);
解(1).由于椭圆的焦点在x轴上,∴设它的标准方程
∴a=5,c=4,∴b =a -c2=25-16=9.
故所求椭圆的标准方程
解(2).由于椭圆的焦点在y轴上,∴设它的标准方程
∴a=2,b=1,
故所求椭圆的标准方程
练习
例3.求适合下列条件的椭圆的标准方程:
(3)经过点A(√3,-2) 和点B(-2√3,1).
解(3):法一(分类讨论法)
①当焦点在x轴上时,设椭圆的标准方程
依题意有 解
故所求椭圆的标准方程
练习
②当焦点在y轴上时,设椭圆的标准方程
依题意 解
∵a>b>0,∴ 无 解 .
例3.求适合下列条件的椭圆的标准方程: (3)经过点A(√3,-2) 和点B(-2√3,1).
解(3):法一(分类讨论法)
练习
设所求椭圆的方程为mx +ny =1((m≠n,m>0,n>0).
依题意 解
故所求椭圆的标准方程
例3.求适合下列条件的椭圆的标准方程: (3)经过点A(√3,-2) 和点B(-2√3,1).
解(3):法二(待定系数法)
练习
方法技巧:
1.利用待定系数法求椭圆标准方程的步骤:
(1)先确定焦点位置;(2)设出方程;(3)寻求a,b,c 的等量关系;(4)求出a,b 的
值,代入所设方程.
2. 当焦点位置不确定时,可设椭圆方程为mx +ny =1(m≠ n,m>0,n>0).
因为它包括焦点在x 轴上(m
分类讨论,从而简化了运算.
变3.求适合下列条件的椭圆的标准方程: (1)经过两点(2,- √2),
解(1):(待定系数法)
设所求椭圆的方程为mx +ny =1((m≠n,
依题意有
故所求椭圆的标准方程
练习
m> 0 ,n>0).
解
变3.求适合下列条件的椭圆的标准方程:
(2)过点( √3,- √5),且与椭 有相同的焦点.
解:∵所求椭圆与椭 有相同的焦点,
∴其焦点在y轴上,且c =25-9=16. 设它的标准方程
∵c =16, 且c =a -b , 故a -b =16.①
又∵点( √3,- √5)在椭圆上, , 即 .②
由①②得b =4,a =20,
所以所求椭圆的标准方程
练习
··
1.椭圆的定义:把平面内与两个定点F ,F 的距离的和等于常数(大于|F F I) 的 点
的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两交点间的距离叫做椭圆的焦距,
焦距的一半称为半焦距.
课堂小结
焦点在x轴上 焦点在y轴上
标准方程 +能=1(a>b>0) +=1(a>b>0)
图形
焦点 (一,0),(c,0) (0,-c),(0,c)
a,b,c 的 关 系 c =a -b
课堂小结
2.椭圆的标准方程:
(1)整理本节课的题型;
(2)课本P109的练习1——4题;
(3)课本P115习题3.1第3、2题。
作业
