全等三角形

课件20张PPT。11.3探索三角形全等的条件（2.1）两边以及其中一边的对角对应相等的两个三角形全等吗？ 以2.5cm，3.5cm为三角形的两边，长度为2.5cm的边所对的角为40°，情况又怎样？动手画一画，
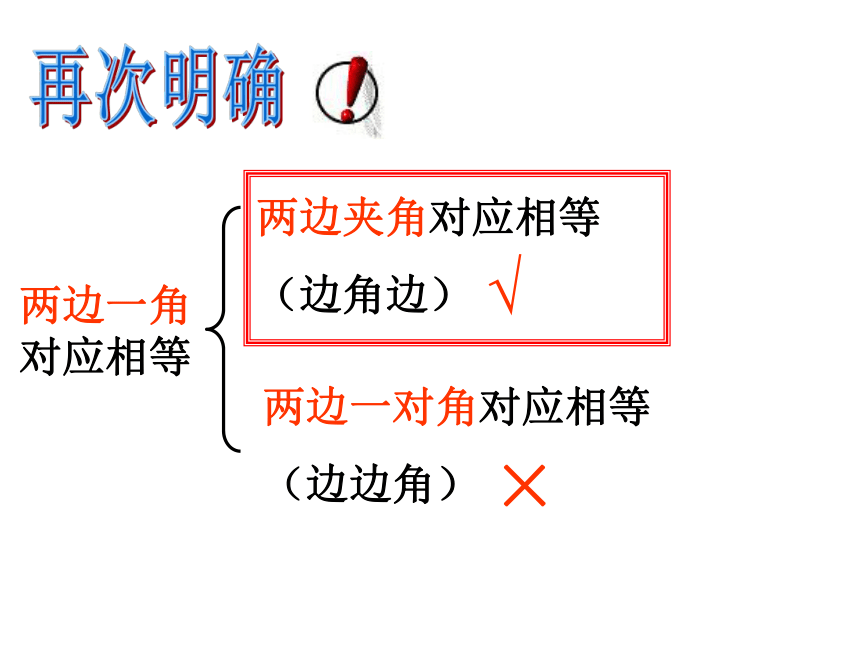
你发现了什么？做一做ABCDEF2.5cm3.5cm40°40°3.5cm2.5cm结论：两边及其中一边所对的角对应相等，两个三角形不一定全等.先画一个40°的角,然后在其中一边上取3.5厘米,最后画40°的角所对的边2.5厘米.两边一角对应相等两边夹角对应相等
（边角边） 两边一对角对应相等
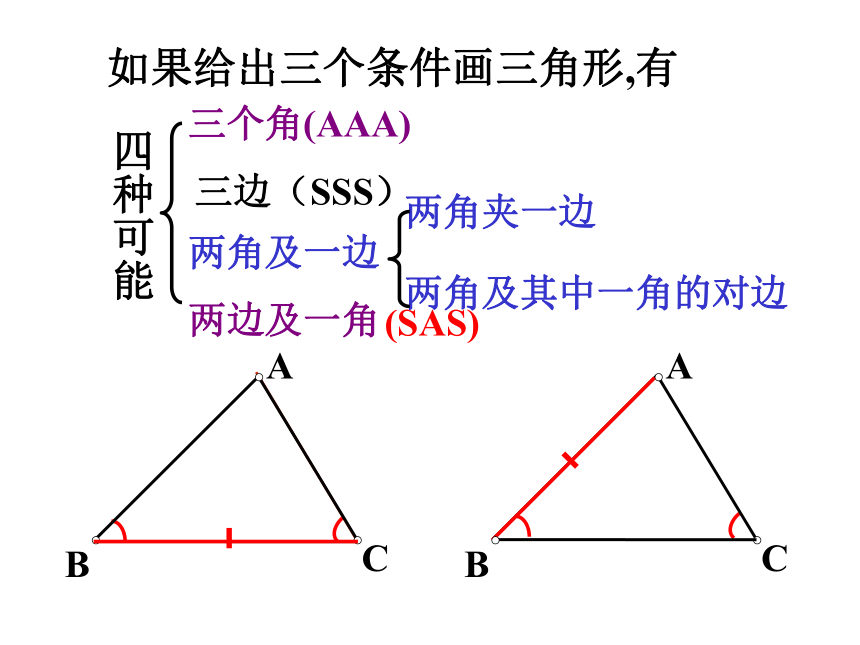
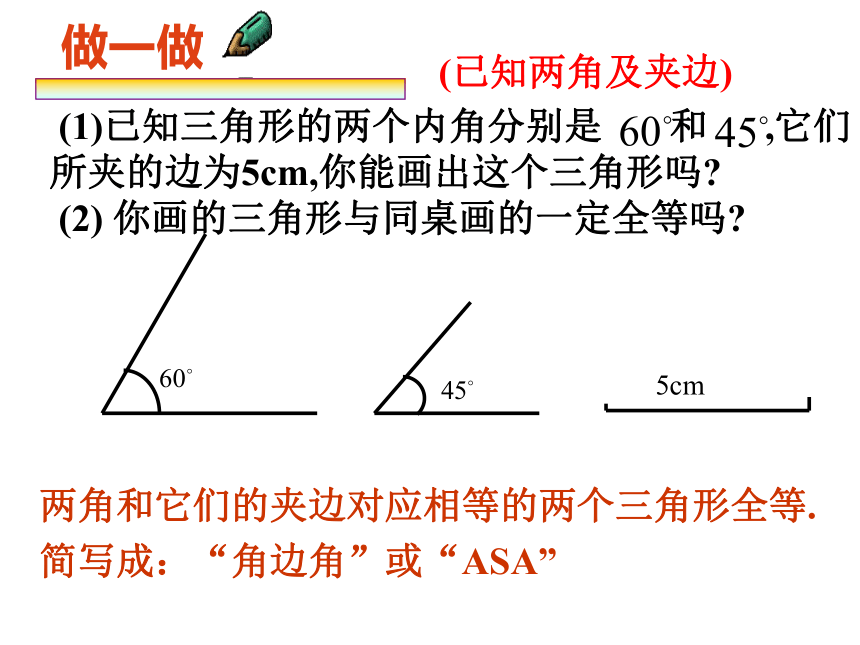
（边边角）×√再次明确如图,小明不慎将一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃吗? 如果可以,带哪块去合适?你能说明其中理由吗?议一议(1)(2)两角夹一边两角及其中一角的对边三边（SSS）两角及一边两边及一角三个角(AAA)四种可能如果给出三个条件画三角形,有(SAS)(已知两角及夹边) (1)已知三角形的两个内角分别是 和 ,它们所夹的边为5cm,你能画出这个三角形吗?
(2) 你画的三角形与同桌画的一定全等吗?5cm做一做两角和它们的夹边对应相等的两个三角形全等.
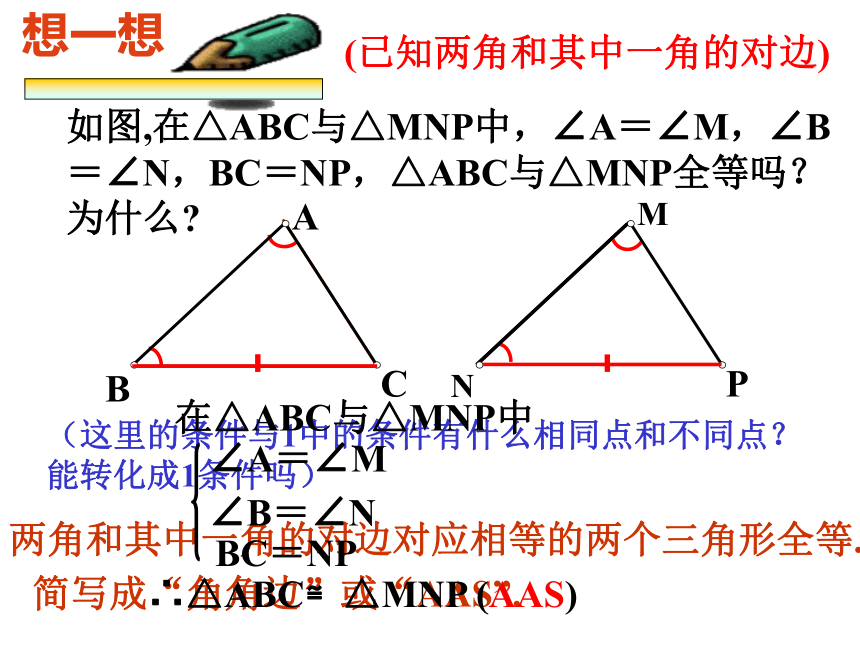
简写成：“角边角”或“ASA”如图,在△ABC与△MNP中，∠C＝∠P，∠B＝∠N，BC＝NP，想一想在△ABC与△MNP中∠A＝∠M∠B＝∠NBC＝NP∴△ABC≌△MNP (ASA)(已知两角和其中一角的对边)如图,在△ABC与△MNP中，∠A＝∠M，∠B＝∠N，BC＝NP，△ABC与△MNP全等吗？为什么?想一想两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.（这里的条件与1中的条件有什么相同点和不同点？能转化成1条件吗）在△ABC与△MNP中∠A＝∠M∠B＝∠NBC＝NP∴△ABC≌△MNP (AAS)如图,小明不慎将一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃吗? 如果可以,带哪块去合适?你能说明其中理由吗?两角和它们的夹边对应相等的两个三角形全等.（ ）在 和 中例1: 如图,O是AB的中点， = ， 与 全等吗?为什么？小明两角和夹边对应相等(已知)(对顶角相等)证明∵点O是AB的中点（已知）
∴AO=BO（中点定义）（已证）≌(1) 图中的两个三角形全等吗? 请说明理由.解：全等.
因为两角和其中一角的对边对应相等
的两个三角形全等.ABCD(已知)(已知)(公共边)=35°=110°练一练(2)已知 和 中, = ,AB=AC.求证: (1) (3) BD=CE证明: (2) AE=AD (全等三角形对应边相等)(已知)(已知)(公共角)(已知)(等式的性质)ABCEDO（３）如图，点B,F,C,E在同一条直线上，∠Ｂ＝∠Ｅ，∠１＝ ∠ ２，ＦＢ＝ＣＥ。△ＡＢＣ与△ＤＥＦ全等吗？为什么？例2、如图,OP是∠MON的角平分线，C是OP上的一点，CA⊥OM，CB⊥ ON，垂足分别为A、B，△AOC与△BOC全等吗？为什么？AB.CABOMNP.C 1、如果改变点C在OP上的位置，那么△AOC与△BOC仍然全等吗？议一议A B2、你能发现什么结论？角平分线上的点到角的两边的距离相等.∵C是∠MON的角平分线OP上一点且CA⊥OM于 A ，CB⊥ ON于B ，CA与CB有什么数量关系？∴CA＝CB
（角平分线上的点到角的两边距离相等）例３如图，∠ABC的平分线与△ABC的外角∠ ACD的平分线相交于点M。试画出点Ｍ到△ABC三边所在直线的垂线段。这三条垂线段的长度相等吗？为什么？小试牛刀NPQ小结(1) 两角和它们的夹边对应相等的两个三角形全等. 简写成“角边角”或“ASA”.(2) 两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.知识要点：(3)探索三角形全等是证明线段相等(对应边相等)，角相等（对应角相等）等问题的基本途径。数学思想：要学会用分类的思想，转化的思想解决问题。作业评价手册
P82 3、 5评价手册P83 6（写在评价上）