【人教版数学八年级上册同步练习】 11.1.与三角形有关的线段本节综合题(含答案)
文档属性
| 名称 | 【人教版数学八年级上册同步练习】 11.1.与三角形有关的线段本节综合题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 16:25:05 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【人教版数学八年级上册同步练习】
11.1.与三角形有关的线段本节综合题
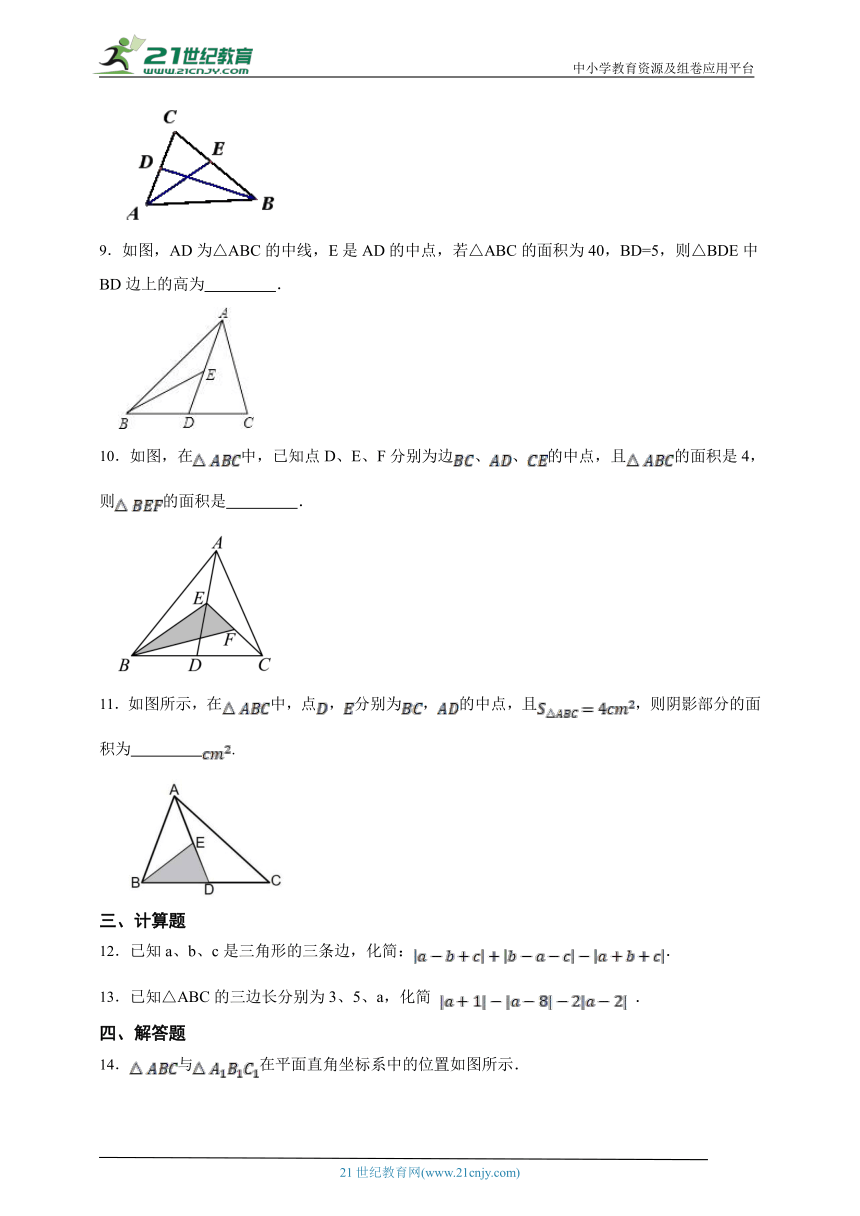
一、单选题
1.下列长度的三条线段,能组成三角形的是( )
A.1,1,2 B.2,3,7 C.1,4,6 D.3,4,5
2.一个三角形的两边长分别为3cm和7cm,则此三角形的第三边的长可能是( )
A.3cm B.4cm C.7cm D.11cm
3.若有两条线段长分别为3cm和4cm,则下列长度的线段能与其组成三角形的是( )
A.1cm B.5cm C.7cm D.9cm
4.小芳有两根长度为4cm和9cm的木条,她想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择长度为( )的木条.
A.5cm B.3 cm C.17cm D.12 cm
5.如果等腰三角形两边长是和,那么它的周长是( )
A. B. C. D.16或
二、填空题
6.下列4种说法中正确的是 .(请填写正确的说法序号).
①一个三角形中至少有两个角为锐角;
②三角形的中线、高线、角平分线都是线段
③同旁内角互补;
④若三条线段的长a、b、c满足,则以a、b、c为边一定能组成三角形
7.如图,工人师傅在安装木制门框时,为防止变形常常钉上两根木条,这样做的依据是 .
8.如图,∠C在三角形中所对的边是 .
9.如图,AD为△ABC的中线,E是AD的中点,若△ABC的面积为40,BD=5,则△BDE中BD边上的高为 .
10.如图,在中,已知点D、E、F分别为边、、的中点,且的面积是4,则的面积是 .
11.如图所示,在中,点,分别为,的中点,且,则阴影部分的面积为 .
三、计算题
12.已知a、b、c是三角形的三条边,化简:.
13.已知△ABC的三边长分别为3、5、a,化简 .
四、解答题
14.与在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A________、B________、C________;
(2)是由经过先向________平移________个单位,再向________平移________个单位平移得到的;
(3)求的面积.
15.从1、2、3、4…、2004中任选k个数,使所选的k个数中一定可以找到能构成三角形边长的三个数(这里要求三角形三边长互不相等),试问满足条件的k的最小值是多少?
16. 如图,在平面直角坐标系中,点,,,,,满足.
图1 图2
(1) , , .
(2)如图1,若点为轴负半轴上的一个动点,连接交轴于点,是否存在点,使得的面积等于的面积?若存在,请求出点的坐标;若不存在,请说明理由;
(3)如图2,若将线段向上平移2个单位长度,点为轴上一点,点为第一象限内的一动点,连接,,,,若的面积等于由,,,四条线段围成的图形的面积,求点的横坐标的值(用含的式子表示).
五、综合题
17.如图,AD、CE是△ABC的两条高,已知AD=10,CE=9,AB=12.
(1)求△ABC的面积;
(2)求BC的长.
18.在长方形 中,边 长度比 长度短10个单位长度,且 的长度是 长度的 .
(1)求 边的长;
(2)现有一动点 从 点出发,以每秒2个单位长度的速度沿折线路径 向终点 运动,在 点运动过程中,设运动时间为 秒,三角形 的面积为 ,试用含 的式子表示 ;
(3)在(2)的条件下,点 为 的中点,点 为 的中点,在点 出发的同时,动点 从点 出发,以4个单位/秒的速度沿 边匀速向左运动,当点 遇到点 后,立即按原速原路返回(调头时间忽略不计),且 回到点 时, 两点立即停止运动.当 时,请求出满足条件的 值?
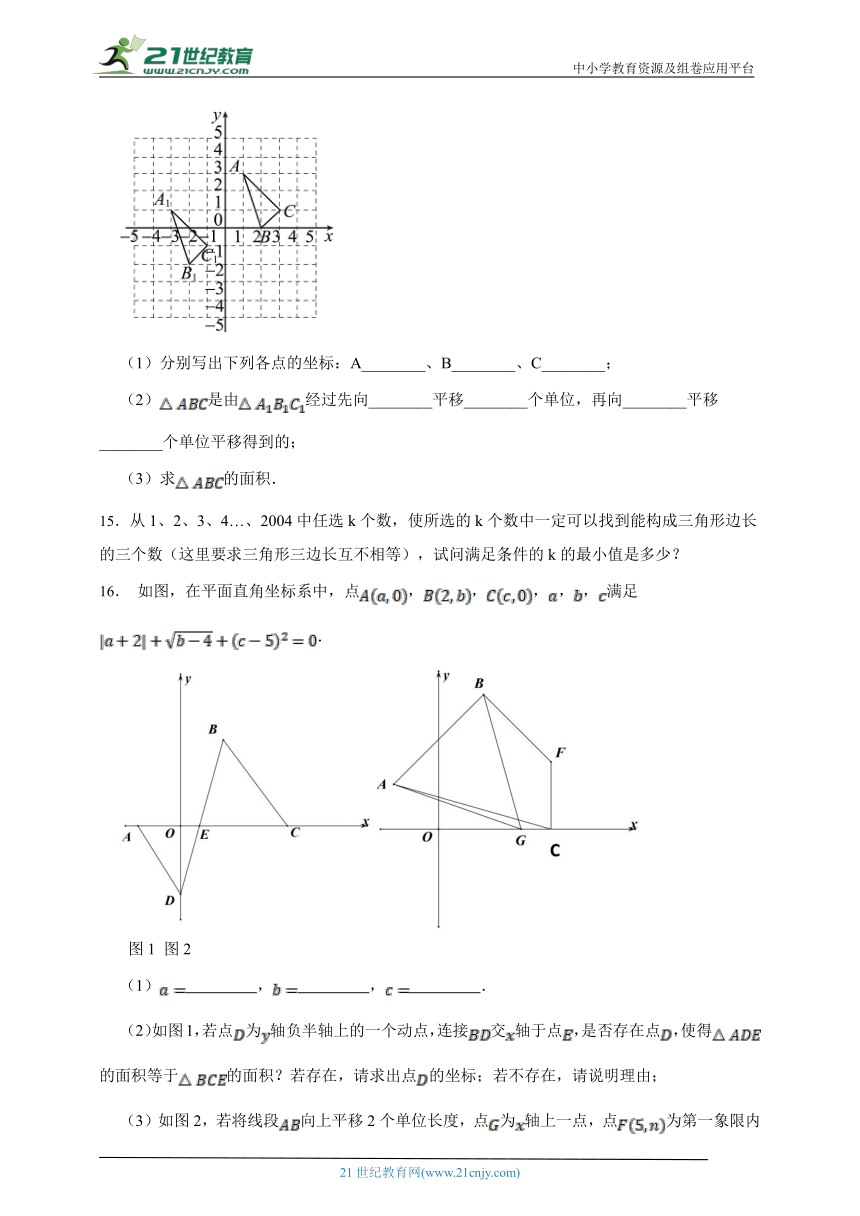
19.如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)
(1)A′、B′两点的坐标分别为A′ 、B′ ;
(2)作出△ABC平移之后的图形△A′B′C′;
(3)求△A′B′C′的面积.
六、实践探究题
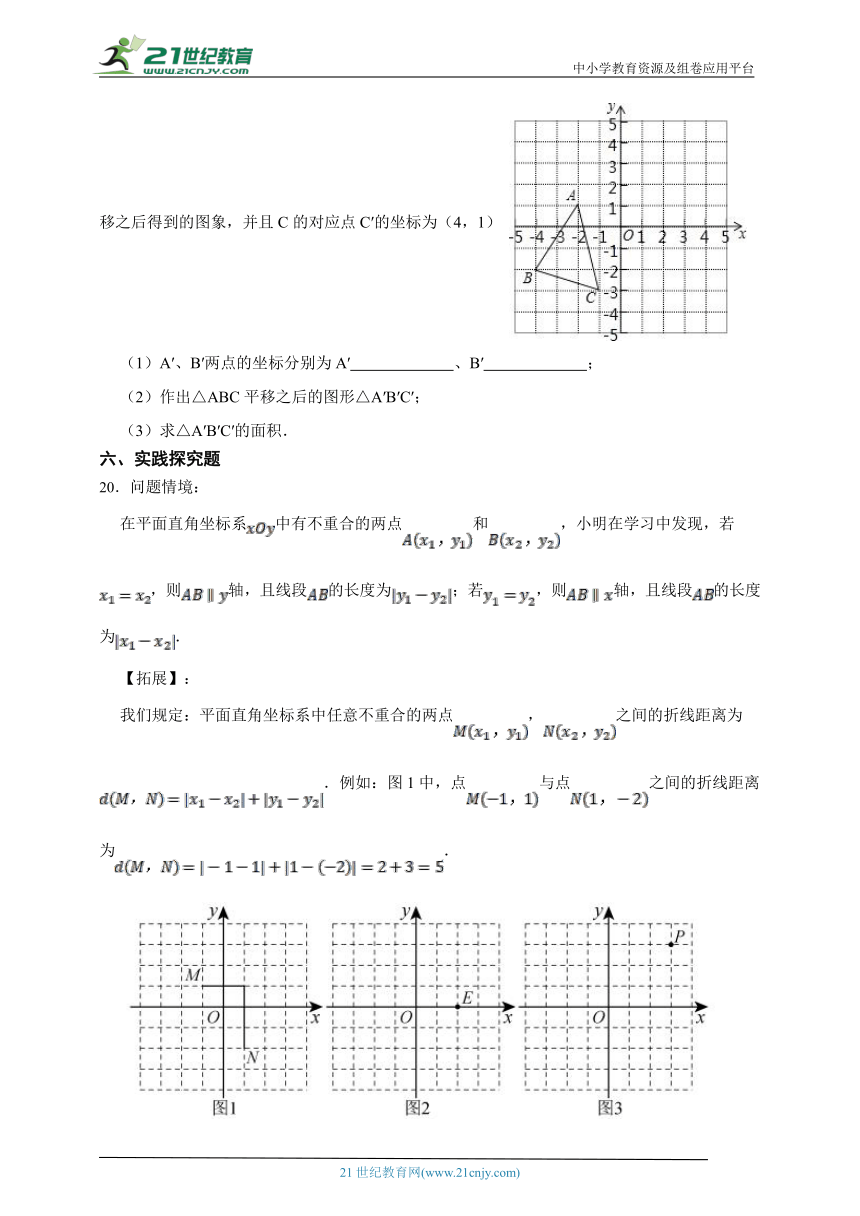
20.问题情境:
在平面直角坐标系中有不重合的两点和,小明在学习中发现,若,则轴,且线段的长度为;若,则轴,且线段的长度为.
【拓展】:
我们规定:平面直角坐标系中任意不重合的两点,之间的折线距离为.例如:图1中,点与点之间的折线距离为.
解决下列问题:
(1)如图2,已知,若,则 ;
(2)如图2,已知,若,则 ;
(3)如图3,已知,点Q在x轴上,且三角形的面积为3,求的值.
答案解析部分
1.【答案】D
【知识点】三角形三边关系
2.【答案】C
【知识点】三角形三边关系
3.【答案】B
【知识点】三角形三边关系
4.【答案】D
【知识点】三角形三边关系
5.【答案】B
【知识点】三角形三边关系
6.【答案】①②
【知识点】三角形三边关系;三角形相关概念;同旁内角的概念
7.【答案】三角形具有稳定性
【知识点】三角形的稳定性
8.【答案】AE,BD,AB
【知识点】三角形相关概念
9.【答案】4
【知识点】三角形的面积
10.【答案】1
【知识点】三角形的角平分线、中线和高
11.【答案】1
【知识点】三角形的角平分线、中线和高;三角形的面积
12.【答案】
【知识点】整式的加减运算;三角形三边关系;化简含绝对值有理数
13.【答案】解:∵△ABC的三边长分别为3、5、a,
∴5 3<a<3+5,
解得:2<a<8,
故|a+1| |a 8| 2|a 2|
=a+1 (8 a) 2(a 2)
=a+1 8+a 2a+4
= 3.
【知识点】三角形三边关系;利用整式的加减运算化简求值
14.【答案】(1),,
(2)左,4,下,2
(3)
【知识点】坐标与图形性质;三角形的面积;坐标与图形变化﹣平移
15.【答案】解:为使k达到最大,可选加入之数等于已得数组中最大的两数之和,这样得:
1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597 ①
共16个数,对符合上述条件的任数组,a1,a2…an显然总有ai大于等于①中的第i个数,
所以n≤16≤k﹣1,
k﹣1≥16,
解得k≥17.
故k的最小值为17.
【知识点】三角形三边关系
16.【答案】(1)-2;4;5
(2)解:连接交轴于点,连接
,
,
(3)解:延长交轴与点,连接.
设,由题意知、,
,
设
或
【知识点】点的坐标;坐标与图形性质;三角形的面积
17.【答案】(1)解:∵CE=9,AB=12,
∴△ABC的面积= ×12×9=54;
(2)解:△ABC的面积= BC AD=54,
即 BC 10=54,
解得BC= .
【知识点】三角形的面积
18.【答案】(1)解: ,
答: 边的长是40个单位长度
(2)解: ,
①当点 在线段 上(不含 点)时, ,
;
②当点 在线段 (不含 点)上时, ,
,
答:三角形 的面积 或
(3)解:点 与点 相遇时: ,解得 (秒),
(一)相遇前:
①当点 在点 右侧时,
,
∵点 是 的中点, ,
,
∵点 是 的中点, ,
,解得 ,
②当点 在点 左侧时,
,
,解得 ,
(二)相遇后:
①当点 在点 左侧时,
,
,解得 ;( 符合题意)
②当点 在点 右侧时,
,
,解得 (舍),
答:当 时, 的值是 或6或
【知识点】三角形的面积;一元一次方程的实际应用-行程问题
19.【答案】(1)(3,5);(1,2)
(2)解:△A′B′C′如图所示;
(3)解:
S△A′B′C′=4×3﹣ ×3×1﹣ ×3×2﹣ ×1×4
=12﹣1.5﹣3﹣2
=5.5
【知识点】三角形的面积;坐标与图形变化﹣平移;作图﹣平移
20.【答案】(1)5
(2)2或
(3)解:由点Q在x轴上,可设点Q的坐标为.
∵三角形OPQ的面积为3.
∴,
解得:;
当点Q的坐标为时,
;
当点Q的坐标为时,
;
综上所述,的值为4或8.
【知识点】线段上的两点间的距离;三角形的面积
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【人教版数学八年级上册同步练习】
11.1.与三角形有关的线段本节综合题
一、单选题
1.下列长度的三条线段,能组成三角形的是( )
A.1,1,2 B.2,3,7 C.1,4,6 D.3,4,5
2.一个三角形的两边长分别为3cm和7cm,则此三角形的第三边的长可能是( )
A.3cm B.4cm C.7cm D.11cm
3.若有两条线段长分别为3cm和4cm,则下列长度的线段能与其组成三角形的是( )
A.1cm B.5cm C.7cm D.9cm
4.小芳有两根长度为4cm和9cm的木条,她想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择长度为( )的木条.
A.5cm B.3 cm C.17cm D.12 cm
5.如果等腰三角形两边长是和,那么它的周长是( )
A. B. C. D.16或
二、填空题
6.下列4种说法中正确的是 .(请填写正确的说法序号).
①一个三角形中至少有两个角为锐角;
②三角形的中线、高线、角平分线都是线段
③同旁内角互补;
④若三条线段的长a、b、c满足,则以a、b、c为边一定能组成三角形
7.如图,工人师傅在安装木制门框时,为防止变形常常钉上两根木条,这样做的依据是 .
8.如图,∠C在三角形中所对的边是 .
9.如图,AD为△ABC的中线,E是AD的中点,若△ABC的面积为40,BD=5,则△BDE中BD边上的高为 .
10.如图,在中,已知点D、E、F分别为边、、的中点,且的面积是4,则的面积是 .
11.如图所示,在中,点,分别为,的中点,且,则阴影部分的面积为 .
三、计算题
12.已知a、b、c是三角形的三条边,化简:.
13.已知△ABC的三边长分别为3、5、a,化简 .
四、解答题
14.与在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A________、B________、C________;
(2)是由经过先向________平移________个单位,再向________平移________个单位平移得到的;
(3)求的面积.
15.从1、2、3、4…、2004中任选k个数,使所选的k个数中一定可以找到能构成三角形边长的三个数(这里要求三角形三边长互不相等),试问满足条件的k的最小值是多少?
16. 如图,在平面直角坐标系中,点,,,,,满足.
图1 图2
(1) , , .
(2)如图1,若点为轴负半轴上的一个动点,连接交轴于点,是否存在点,使得的面积等于的面积?若存在,请求出点的坐标;若不存在,请说明理由;
(3)如图2,若将线段向上平移2个单位长度,点为轴上一点,点为第一象限内的一动点,连接,,,,若的面积等于由,,,四条线段围成的图形的面积,求点的横坐标的值(用含的式子表示).
五、综合题
17.如图,AD、CE是△ABC的两条高,已知AD=10,CE=9,AB=12.
(1)求△ABC的面积;
(2)求BC的长.
18.在长方形 中,边 长度比 长度短10个单位长度,且 的长度是 长度的 .
(1)求 边的长;
(2)现有一动点 从 点出发,以每秒2个单位长度的速度沿折线路径 向终点 运动,在 点运动过程中,设运动时间为 秒,三角形 的面积为 ,试用含 的式子表示 ;
(3)在(2)的条件下,点 为 的中点,点 为 的中点,在点 出发的同时,动点 从点 出发,以4个单位/秒的速度沿 边匀速向左运动,当点 遇到点 后,立即按原速原路返回(调头时间忽略不计),且 回到点 时, 两点立即停止运动.当 时,请求出满足条件的 值?
19.如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)
(1)A′、B′两点的坐标分别为A′ 、B′ ;
(2)作出△ABC平移之后的图形△A′B′C′;
(3)求△A′B′C′的面积.
六、实践探究题
20.问题情境:
在平面直角坐标系中有不重合的两点和,小明在学习中发现,若,则轴,且线段的长度为;若,则轴,且线段的长度为.
【拓展】:
我们规定:平面直角坐标系中任意不重合的两点,之间的折线距离为.例如:图1中,点与点之间的折线距离为.
解决下列问题:
(1)如图2,已知,若,则 ;
(2)如图2,已知,若,则 ;
(3)如图3,已知,点Q在x轴上,且三角形的面积为3,求的值.
答案解析部分
1.【答案】D
【知识点】三角形三边关系
2.【答案】C
【知识点】三角形三边关系
3.【答案】B
【知识点】三角形三边关系
4.【答案】D
【知识点】三角形三边关系
5.【答案】B
【知识点】三角形三边关系
6.【答案】①②
【知识点】三角形三边关系;三角形相关概念;同旁内角的概念
7.【答案】三角形具有稳定性
【知识点】三角形的稳定性
8.【答案】AE,BD,AB
【知识点】三角形相关概念
9.【答案】4
【知识点】三角形的面积
10.【答案】1
【知识点】三角形的角平分线、中线和高
11.【答案】1
【知识点】三角形的角平分线、中线和高;三角形的面积
12.【答案】
【知识点】整式的加减运算;三角形三边关系;化简含绝对值有理数
13.【答案】解:∵△ABC的三边长分别为3、5、a,
∴5 3<a<3+5,
解得:2<a<8,
故|a+1| |a 8| 2|a 2|
=a+1 (8 a) 2(a 2)
=a+1 8+a 2a+4
= 3.
【知识点】三角形三边关系;利用整式的加减运算化简求值
14.【答案】(1),,
(2)左,4,下,2
(3)
【知识点】坐标与图形性质;三角形的面积;坐标与图形变化﹣平移
15.【答案】解:为使k达到最大,可选加入之数等于已得数组中最大的两数之和,这样得:
1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597 ①
共16个数,对符合上述条件的任数组,a1,a2…an显然总有ai大于等于①中的第i个数,
所以n≤16≤k﹣1,
k﹣1≥16,
解得k≥17.
故k的最小值为17.
【知识点】三角形三边关系
16.【答案】(1)-2;4;5
(2)解:连接交轴于点,连接
,
,
(3)解:延长交轴与点,连接.
设,由题意知、,
,
设
或
【知识点】点的坐标;坐标与图形性质;三角形的面积
17.【答案】(1)解:∵CE=9,AB=12,
∴△ABC的面积= ×12×9=54;
(2)解:△ABC的面积= BC AD=54,
即 BC 10=54,
解得BC= .
【知识点】三角形的面积
18.【答案】(1)解: ,
答: 边的长是40个单位长度
(2)解: ,
①当点 在线段 上(不含 点)时, ,
;
②当点 在线段 (不含 点)上时, ,
,
答:三角形 的面积 或
(3)解:点 与点 相遇时: ,解得 (秒),
(一)相遇前:
①当点 在点 右侧时,
,
∵点 是 的中点, ,
,
∵点 是 的中点, ,
,解得 ,
②当点 在点 左侧时,
,
,解得 ,
(二)相遇后:
①当点 在点 左侧时,
,
,解得 ;( 符合题意)
②当点 在点 右侧时,
,
,解得 (舍),
答:当 时, 的值是 或6或
【知识点】三角形的面积;一元一次方程的实际应用-行程问题
19.【答案】(1)(3,5);(1,2)
(2)解:△A′B′C′如图所示;
(3)解:
S△A′B′C′=4×3﹣ ×3×1﹣ ×3×2﹣ ×1×4
=12﹣1.5﹣3﹣2
=5.5
【知识点】三角形的面积;坐标与图形变化﹣平移;作图﹣平移
20.【答案】(1)5
(2)2或
(3)解:由点Q在x轴上,可设点Q的坐标为.
∵三角形OPQ的面积为3.
∴,
解得:;
当点Q的坐标为时,
;
当点Q的坐标为时,
;
综上所述,的值为4或8.
【知识点】线段上的两点间的距离;三角形的面积
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
