6.2.2 排列数 (教学课件)(共16张PPT)-高中数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 6.2.2 排列数 (教学课件)(共16张PPT)-高中数学人教A版(2019)选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-16 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
1、理解排列数的意义;
2、会用排列解决简单的计数问题;
3、经历将简单的计数问题划归为排列问题的过程,从中体会 “化归”的数学思想.
4、能运用所学的排列知识,正确地解决实际问题,体会“化 归”思想的魅力.
教学目标
1.排列的定义:
一般地,从n个不同元素中取出m(m≤n)个元素,并按照 一定的顺序排成一列,叫做从n个不同元素中取出m 个元素的 一 个排列(arrangement).
2.排列问题的判断方法:
(1)元素的无重复性
(2)元素的有序性
(3)判断的关键:变换元素的位置,看结果是否发生变化, 有变化是有序,无变化就是无序.
复习回顾
问题1 从甲、乙、丙3名同学中选出2名参加一项活动,其中1名 同学参加上午的活动,另1名同学参加下午的活动,有多少种不 同的选法
问题2 从1,2,3, 4这4个数字中,每次取出3个排成一个三位数, 共可得到多少个不同的三位数
引入:通过上节课中的问题1和问题2,我们学习了排列的定义 ,并利用分步乘法计数原理或列举法计算排列的个数,但是如 果元素增多,这样的表达和计算方法会显得繁琐冗长.简化一 直是数学的追求,能进一步实现对排列问题的简化运算吗
新课导入
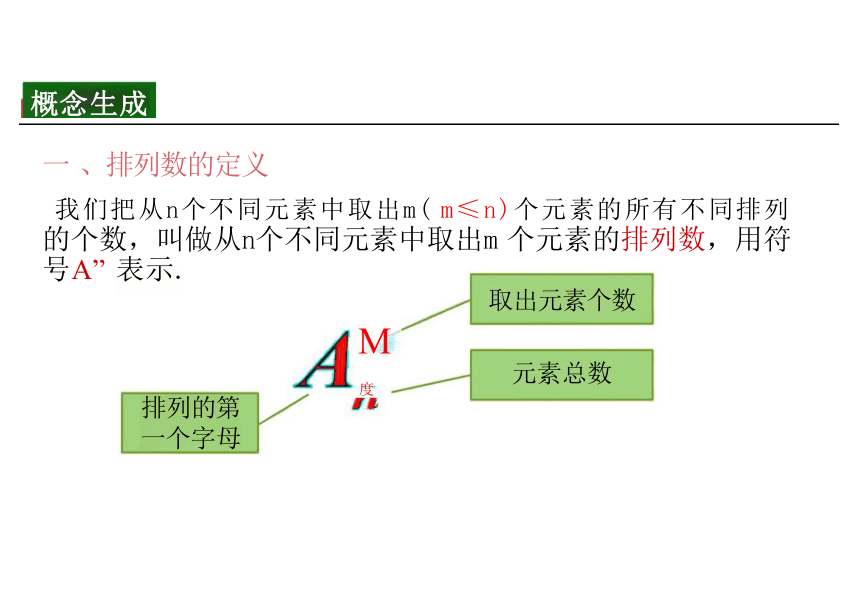
号A” 表示.
取出元素个数
M
元素总数
度
排列的第
一个字母
一 、排列数的定义
我们把从n个不同元素中取出m( m≤n)个元素的所有不同排列 的个数,叫做从n个不同元素中取出m 个元素的排列数,用符
概念生成
追问1“从n个不同元素中取出m(m≤n)个元素,并按照一定的 顺序排成一列”与“从n个不同元素中取出m(m≤n)个元素的 排列数”是同一回事吗
排列是指从n个不同元素中取出m(m≤n)个元素,排成一列的 具体排法,也就是完成一件事的一种方法,它不是数;
排列数是指从n个不同元素中取出m(m≤n)个元素,排成一列所 有排列的个数,它是一个数.
追 问 2 你能用排列数符号表示上节课中的问题1和问题2吗 问题1: 。 问题2:
概念辨析
新知探究 探究:排列数公式的推导
探究研究了排列数的符号表达,是否有排列数公式便捷的求出排列个 数从n个不同元素中取出m个元素的排列数A"(m≤n)是多少
第一位 第二位 第三位 第四位 第m位
n n-1 n-2 n-3 n-m+1
(1)从n个元素中取出2个元素的排列数: n-1)
(2)从n个元素中取出3个元素的排列数:
(3)从n个元素中取出4个元素的排列数:
从n个元素中取出m 个元素的排列数:Am=n(n-1)(n-2)…(n-m+1)
2
二 、排列数公式
A"=n(n-1)(m-2)…(n 一 阴+1) .(m,m∈N 且m≤n)
问题2观察排列数公式的结构,回答下列问题:
(1)观察公式的右边,有什么特点 共有几个因数
(2)比较n与m 的大小关系,公式右边的最后一个因数又有 什么特点
(3)若m=n 时 ,A 的表达式有什么特点
概念生成
三 、全排列数
1.全排列:从n个不同素中取出n个元素的一个排列称为n个 不同元素的一个全排列.
全排列数为:A”=m(-1)(m-2)… ×2×1
2.阶乘:正整数1到n的连乘积1×2×…×n 称为n的阶乘, 用n! 表示,即
概念生成
规定:01=1。
追问观察例3的运算结果,你有什么发现 能推广到一般 情况吗
典例剖析
例3计算:
2、全排列公式:
An=n(n-1)(n-2)···3×2×1=n!
1、排列数公式:
归纳整理
2
9
解法三:
百位 十 位 个 位 百 位 十 位 个 位
0
3种 A 种
百位 十位 个位
百位 十位 个位
0
9
百位
0
例4用0~9这10个数字,可以组成多少个没有重复数字的三
百位 十位 个位
解法二 :
位数
解法一:
典例剖析
十位
个位
位置分析法 以位置为主,优先 考虑特殊位置
分步
直接法
元素分析法 以元素为主,优 先考虑特殊元素
先分类
后分步
先不考虑限制条件,计算出来所有排列
数,再从中减去全部不符合条件的排列 数,从而得出符合条件的排列数
带有限制条件的排列问题:“特殊”优先原则
方法归纳
间接法
(2)0在十位的有A4A个;
(3)没有0的有A4A 个.
共 有 A +A Ag+A A =328 (个).
变式用0~9这些数字,能组成多少个没有重复数字的三位数 且是偶数
解:(1)0在个位的有A3个;
0
0
变式训练
3.若n∈N,则(55-n)(56-n) · (68-n)(69-n) 用排列数符号表示为:
4.一个火车站有8股岔道,如果每股道只能停放1列火车,现要停放4列不 同的火车,共有多少种不同的停放方法
1.求证:(1) ; (2)
小试牛刀
,m=
1、理解排列数的意义;
2、会用排列解决简单的计数问题;
3、经历将简单的计数问题划归为排列问题的过程,从中体会 “化归”的数学思想.
4、能运用所学的排列知识,正确地解决实际问题,体会“化 归”思想的魅力.
教学目标
1.排列的定义:
一般地,从n个不同元素中取出m(m≤n)个元素,并按照 一定的顺序排成一列,叫做从n个不同元素中取出m 个元素的 一 个排列(arrangement).
2.排列问题的判断方法:
(1)元素的无重复性
(2)元素的有序性
(3)判断的关键:变换元素的位置,看结果是否发生变化, 有变化是有序,无变化就是无序.
复习回顾
问题1 从甲、乙、丙3名同学中选出2名参加一项活动,其中1名 同学参加上午的活动,另1名同学参加下午的活动,有多少种不 同的选法
问题2 从1,2,3, 4这4个数字中,每次取出3个排成一个三位数, 共可得到多少个不同的三位数
引入:通过上节课中的问题1和问题2,我们学习了排列的定义 ,并利用分步乘法计数原理或列举法计算排列的个数,但是如 果元素增多,这样的表达和计算方法会显得繁琐冗长.简化一 直是数学的追求,能进一步实现对排列问题的简化运算吗
新课导入
号A” 表示.
取出元素个数
M
元素总数
度
排列的第
一个字母
一 、排列数的定义
我们把从n个不同元素中取出m( m≤n)个元素的所有不同排列 的个数,叫做从n个不同元素中取出m 个元素的排列数,用符
概念生成
追问1“从n个不同元素中取出m(m≤n)个元素,并按照一定的 顺序排成一列”与“从n个不同元素中取出m(m≤n)个元素的 排列数”是同一回事吗
排列是指从n个不同元素中取出m(m≤n)个元素,排成一列的 具体排法,也就是完成一件事的一种方法,它不是数;
排列数是指从n个不同元素中取出m(m≤n)个元素,排成一列所 有排列的个数,它是一个数.
追 问 2 你能用排列数符号表示上节课中的问题1和问题2吗 问题1: 。 问题2:
概念辨析
新知探究 探究:排列数公式的推导
探究研究了排列数的符号表达,是否有排列数公式便捷的求出排列个 数从n个不同元素中取出m个元素的排列数A"(m≤n)是多少
第一位 第二位 第三位 第四位 第m位
n n-1 n-2 n-3 n-m+1
(1)从n个元素中取出2个元素的排列数: n-1)
(2)从n个元素中取出3个元素的排列数:
(3)从n个元素中取出4个元素的排列数:
从n个元素中取出m 个元素的排列数:Am=n(n-1)(n-2)…(n-m+1)
2
二 、排列数公式
A"=n(n-1)(m-2)…(n 一 阴+1) .(m,m∈N 且m≤n)
问题2观察排列数公式的结构,回答下列问题:
(1)观察公式的右边,有什么特点 共有几个因数
(2)比较n与m 的大小关系,公式右边的最后一个因数又有 什么特点
(3)若m=n 时 ,A 的表达式有什么特点
概念生成
三 、全排列数
1.全排列:从n个不同素中取出n个元素的一个排列称为n个 不同元素的一个全排列.
全排列数为:A”=m(-1)(m-2)… ×2×1
2.阶乘:正整数1到n的连乘积1×2×…×n 称为n的阶乘, 用n! 表示,即
概念生成
规定:01=1。
追问观察例3的运算结果,你有什么发现 能推广到一般 情况吗
典例剖析
例3计算:
2、全排列公式:
An=n(n-1)(n-2)···3×2×1=n!
1、排列数公式:
归纳整理
2
9
解法三:
百位 十 位 个 位 百 位 十 位 个 位
0
3种 A 种
百位 十位 个位
百位 十位 个位
0
9
百位
0
例4用0~9这10个数字,可以组成多少个没有重复数字的三
百位 十位 个位
解法二 :
位数
解法一:
典例剖析
十位
个位
位置分析法 以位置为主,优先 考虑特殊位置
分步
直接法
元素分析法 以元素为主,优 先考虑特殊元素
先分类
后分步
先不考虑限制条件,计算出来所有排列
数,再从中减去全部不符合条件的排列 数,从而得出符合条件的排列数
带有限制条件的排列问题:“特殊”优先原则
方法归纳
间接法
(2)0在十位的有A4A个;
(3)没有0的有A4A 个.
共 有 A +A Ag+A A =328 (个).
变式用0~9这些数字,能组成多少个没有重复数字的三位数 且是偶数
解:(1)0在个位的有A3个;
0
0
变式训练
3.若n∈N,则(55-n)(56-n) · (68-n)(69-n) 用排列数符号表示为:
4.一个火车站有8股岔道,如果每股道只能停放1列火车,现要停放4列不 同的火车,共有多少种不同的停放方法
1.求证:(1) ; (2)
小试牛刀
,m=
