北京一零一中学2023-2024学年度高一第二学期数学统练四(PDF版,无答案)
文档属性
| 名称 | 北京一零一中学2023-2024学年度高一第二学期数学统练四(PDF版,无答案) | 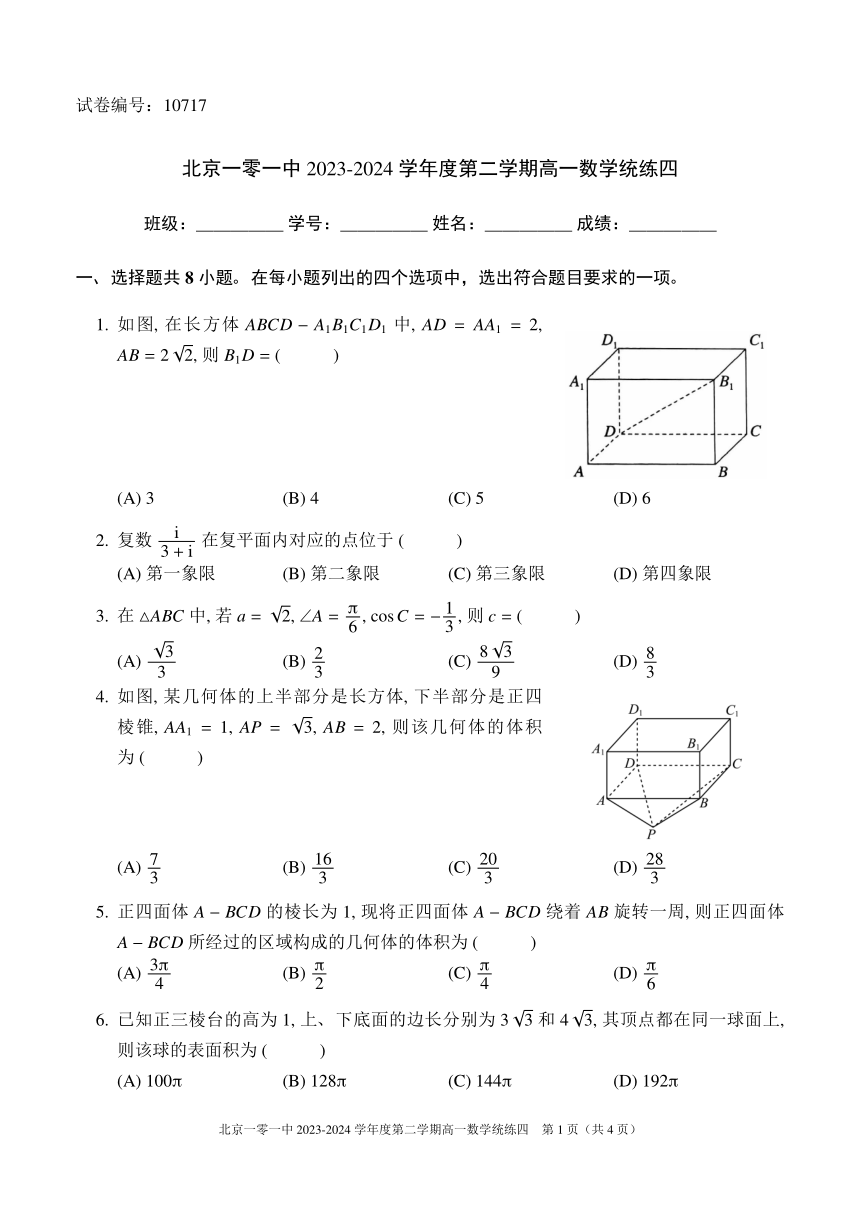 | |
| 格式 | |||
| 文件大小 | 187.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-15 14:26:22 | ||
图片预览


文档简介
试卷编号:10717 北京一零一中题库管理系统 Q9999
北京一零一中 2023-2024学年度第二学期高一数学统练四
班级:_____学号:_____姓名:_____成绩:_____
一、选择题共 8小题。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 如图, 在长方体 ABCD A1B1C1D1 中, AD = AA1 = 2,
√
AB = 2 2,则 B1D = ( )
(A) 3 (B) 4 (C) 5 (D) 6
2. 复数 i 在复平面内对应的点位于 ( )
3 + i
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
√
3. 在 △ABC中,若 a = 2, ∠A π= , cos C 1= ,则 c = ( )
√ 6 3 √
(A) 3 (B) 2 (C) 8 3 (D) 8
3 3 9 3
4. 如图, 某几何体的上半部分是长方体, 下半部分是正四
√
棱锥, AA1 = 1, AP = 3, AB = 2, 则该几何体的体积
为 ( )
(A) 7 (B) 16 (C) 20 (D) 28
3 3 3 3
5. 正四面体 A BCD的棱长为 1,现将正四面体 A BCD绕着 AB旋转一周,则正四面体
A BCD所经过的区域构成的几何体的体积为 ( )
(A) 3π (B) π (C) π (D) π
4 2 4 6
√ √
6. 已知正三棱台的高为 1,上、下底面的边长分别为 3 3和 4 3,其顶点都在同一球面上,
则该球的表面积为 ( )
(A) 100π (B) 128π (C) 144π (D) 192π
北京一零一中 2023-2024学年度第二学期高一数学统练四 第 1页(共 4页)
√
7. 如图,甲船以每小时 30 2海里的速度向正北方向航行,
乙船按固定方向匀速直线航行,当甲船位于 A1 处时,乙
船位于甲船的北偏西 105 方向的 B1 处, 此时两船相距
20 海里, 当甲船航行 20 分钟到达 A2 处时, 乙船航行到
√
甲船的北偏西 120 方向的 B2 处,此时两船相距 10 2海
里,则乙船每小时航行 ( )
√ √ √
(A) 10 2海里 (B) 20 2海里 (C) 30海里 (D) 30 2海里
√
8. 在 △ABC 中,角 A, B, C 的对边分别为 a, b, c. 若 a cos C + 3a sin C b c = 0,则 △ABC
外接圆√面积与 △ABC面积之√比的最小值为 ( √) √
(A) 2 3 (B) 4 3 (C) 8 3 (D) 16 3π π π π
9 9 9 9
二、填空题共 6小题。
9. 一圆锥的侧面展开图为一圆心角为 2π 的扇形, 该圆锥母线长为 6, 则圆锥的底面半径
3
为_____ .
√
10. 在△ABC中,内角 A, B, C的对边分别为 a, b, c,且 b 2 c = a cos C,则∠A =_____ .
2
11. 已知 z1 = 2 2i,且 |z| = 1,则 |z z1|的最大值为_____ .
12. 已知点 S , A, B, C 均在半径为 2的球面上, △ABC 是边长为 3的等边三角形, S A ⊥平面
ABC,则 S A =_____ .
13. 如图,四面体 ABCD的一条棱长为 x,其余棱长均为 2,记
四面体 ABCD 的表面积为 F(x), 则函数 F(x) 的定义域
为_____ ;最大值为_____ .
√
14. 在 △ABC , A, B, C a, b, c, 3c中 角 的对边分别为 = tan A + tan B. 给出下列四个结论:
a cos B
① A π= ;
3 √
②当 a = 2, c ∈ (2, 2 2)时,满足条件的 △ABC有 2个;
√
③若 AD是 ∠BAC的平分线,且 AD = 2 3. 则 1 1+ = 2;
√ b c
b c 3a④当 = 时, △ABC为直角三角形.
3
其中所有正确结论的序号是_____ .
北京一零一中 2023-2024学年度第二学期高一数学统练四 第 2页(共 4页)
三、解答题共 3小题。解答应写出文字说明、演算步骤或证明过程。
√
15. 已知 △ABC 9 3是面积为 的等边三角形,且其顶点都在以 O为球心的球面上. 若球 O
4
的体积为 32π ,求球心 O到平面 ABC的距离.
3
√ √
16. 如图,在 △ABC中, ∠B π= , D为 BC边上一点,且 cos∠ADC 2 7= , AD = 7.
6 7
(1)求 AB的长及 sin∠DAB的值;
(2)若 S △ADB : S △A√CD = 1 : 4,求 △ACD的周长;
(3) 5 3若 S △ACB = ,求 △ACD中 AD边上的高.2
北京一零一中 2023-2024学年度第二学期高一数学统练四 第 3页(共 4页)
√
17. 已知函数 f (x) = 2 3 sinωx cosωx + 2 cos2 ωx (ω > 0)的最小正周期为 π.
(1)求 ω的值;
(2)在锐角三角形 ABC中,角 A, B, C所对的边分别为 a, b, c. c为 f (x)在 [0, π ]上的最大
2
值,再从条件①、条件②、条件③这三个条件中选择一个作为已知,求 a b的取值范围.
条件①: a cos B + b cos A = 2c cos C;
√
条件②: 2a sin A cos B + b sin 2A = 3√a;
3(a2 + b2 c2)
条件③: △ABC的面积为 S ,且 S = .
4
北京一零一中 2023-2024学年度第二学期高一数学统练四 第 4页(共 4页)
北京一零一中 2023-2024学年度第二学期高一数学统练四
班级:_____学号:_____姓名:_____成绩:_____
一、选择题共 8小题。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 如图, 在长方体 ABCD A1B1C1D1 中, AD = AA1 = 2,
√
AB = 2 2,则 B1D = ( )
(A) 3 (B) 4 (C) 5 (D) 6
2. 复数 i 在复平面内对应的点位于 ( )
3 + i
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
√
3. 在 △ABC中,若 a = 2, ∠A π= , cos C 1= ,则 c = ( )
√ 6 3 √
(A) 3 (B) 2 (C) 8 3 (D) 8
3 3 9 3
4. 如图, 某几何体的上半部分是长方体, 下半部分是正四
√
棱锥, AA1 = 1, AP = 3, AB = 2, 则该几何体的体积
为 ( )
(A) 7 (B) 16 (C) 20 (D) 28
3 3 3 3
5. 正四面体 A BCD的棱长为 1,现将正四面体 A BCD绕着 AB旋转一周,则正四面体
A BCD所经过的区域构成的几何体的体积为 ( )
(A) 3π (B) π (C) π (D) π
4 2 4 6
√ √
6. 已知正三棱台的高为 1,上、下底面的边长分别为 3 3和 4 3,其顶点都在同一球面上,
则该球的表面积为 ( )
(A) 100π (B) 128π (C) 144π (D) 192π
北京一零一中 2023-2024学年度第二学期高一数学统练四 第 1页(共 4页)
√
7. 如图,甲船以每小时 30 2海里的速度向正北方向航行,
乙船按固定方向匀速直线航行,当甲船位于 A1 处时,乙
船位于甲船的北偏西 105 方向的 B1 处, 此时两船相距
20 海里, 当甲船航行 20 分钟到达 A2 处时, 乙船航行到
√
甲船的北偏西 120 方向的 B2 处,此时两船相距 10 2海
里,则乙船每小时航行 ( )
√ √ √
(A) 10 2海里 (B) 20 2海里 (C) 30海里 (D) 30 2海里
√
8. 在 △ABC 中,角 A, B, C 的对边分别为 a, b, c. 若 a cos C + 3a sin C b c = 0,则 △ABC
外接圆√面积与 △ABC面积之√比的最小值为 ( √) √
(A) 2 3 (B) 4 3 (C) 8 3 (D) 16 3π π π π
9 9 9 9
二、填空题共 6小题。
9. 一圆锥的侧面展开图为一圆心角为 2π 的扇形, 该圆锥母线长为 6, 则圆锥的底面半径
3
为_____ .
√
10. 在△ABC中,内角 A, B, C的对边分别为 a, b, c,且 b 2 c = a cos C,则∠A =_____ .
2
11. 已知 z1 = 2 2i,且 |z| = 1,则 |z z1|的最大值为_____ .
12. 已知点 S , A, B, C 均在半径为 2的球面上, △ABC 是边长为 3的等边三角形, S A ⊥平面
ABC,则 S A =_____ .
13. 如图,四面体 ABCD的一条棱长为 x,其余棱长均为 2,记
四面体 ABCD 的表面积为 F(x), 则函数 F(x) 的定义域
为_____ ;最大值为_____ .
√
14. 在 △ABC , A, B, C a, b, c, 3c中 角 的对边分别为 = tan A + tan B. 给出下列四个结论:
a cos B
① A π= ;
3 √
②当 a = 2, c ∈ (2, 2 2)时,满足条件的 △ABC有 2个;
√
③若 AD是 ∠BAC的平分线,且 AD = 2 3. 则 1 1+ = 2;
√ b c
b c 3a④当 = 时, △ABC为直角三角形.
3
其中所有正确结论的序号是_____ .
北京一零一中 2023-2024学年度第二学期高一数学统练四 第 2页(共 4页)
三、解答题共 3小题。解答应写出文字说明、演算步骤或证明过程。
√
15. 已知 △ABC 9 3是面积为 的等边三角形,且其顶点都在以 O为球心的球面上. 若球 O
4
的体积为 32π ,求球心 O到平面 ABC的距离.
3
√ √
16. 如图,在 △ABC中, ∠B π= , D为 BC边上一点,且 cos∠ADC 2 7= , AD = 7.
6 7
(1)求 AB的长及 sin∠DAB的值;
(2)若 S △ADB : S △A√CD = 1 : 4,求 △ACD的周长;
(3) 5 3若 S △ACB = ,求 △ACD中 AD边上的高.2
北京一零一中 2023-2024学年度第二学期高一数学统练四 第 3页(共 4页)
√
17. 已知函数 f (x) = 2 3 sinωx cosωx + 2 cos2 ωx (ω > 0)的最小正周期为 π.
(1)求 ω的值;
(2)在锐角三角形 ABC中,角 A, B, C所对的边分别为 a, b, c. c为 f (x)在 [0, π ]上的最大
2
值,再从条件①、条件②、条件③这三个条件中选择一个作为已知,求 a b的取值范围.
条件①: a cos B + b cos A = 2c cos C;
√
条件②: 2a sin A cos B + b sin 2A = 3√a;
3(a2 + b2 c2)
条件③: △ABC的面积为 S ,且 S = .
4
北京一零一中 2023-2024学年度第二学期高一数学统练四 第 4页(共 4页)
同课章节目录
