【人教版数学八年级上册同步练习】 第十一章三角形综合检测题(含答案)
文档属性
| 名称 | 【人教版数学八年级上册同步练习】 第十一章三角形综合检测题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-15 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【人教版数学八年级上册同步练习】
第十一章三角形综合检测题
一、单选题
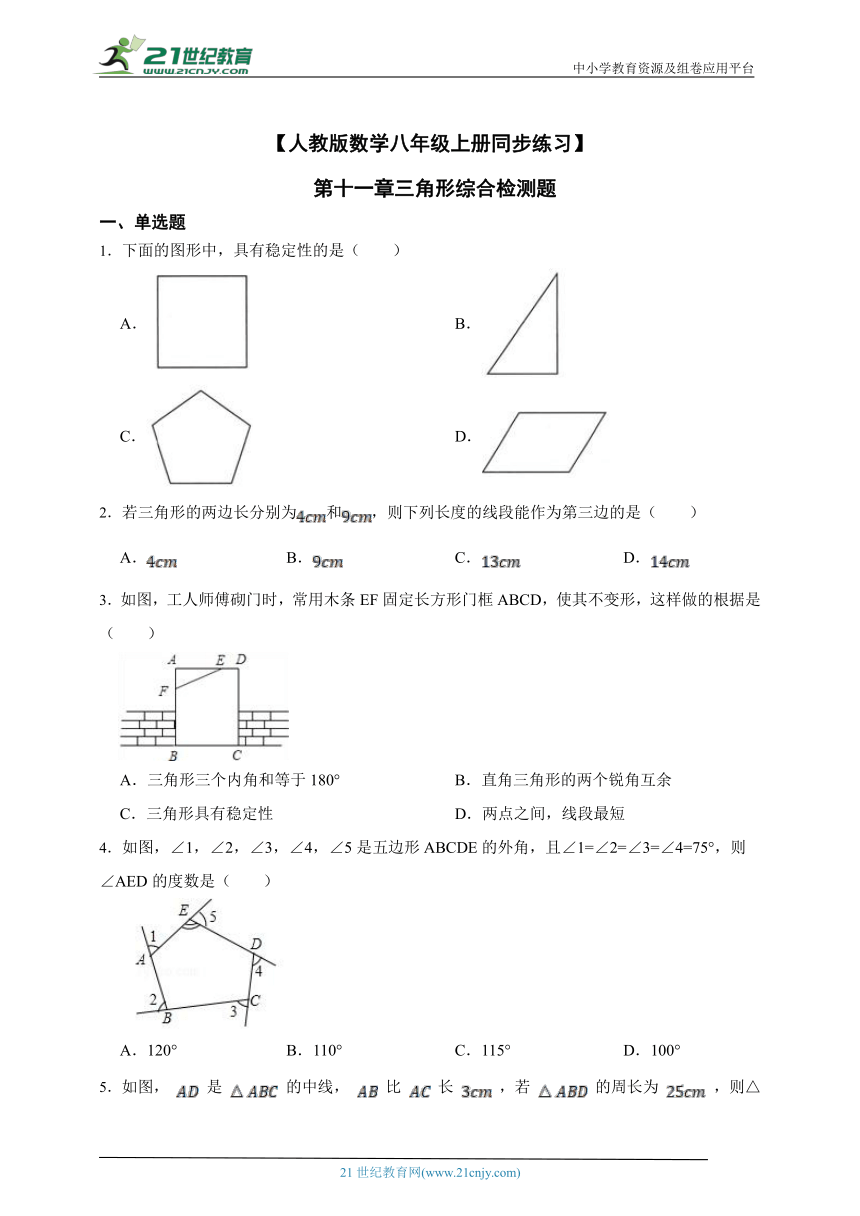
1.下面的图形中,具有稳定性的是( )
A. B.
C. D.
2.若三角形的两边长分别为和,则下列长度的线段能作为第三边的是( )
A. B. C. D.
3.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A.三角形三个内角和等于180° B.直角三角形的两个锐角互余
C.三角形具有稳定性 D.两点之间,线段最短
4.如图,∠1,∠2,∠3,∠4,∠5是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=75°,则∠AED的度数是( )
A.120° B.110° C.115° D.100°
5.如图, 是 的中线, 比 长 ,若 的周长为 ,则△ 的周长为( )
A. B. C. D.
二、填空题
6.如图,在中,点、分别是、的中点,,则= .
7.如图所示,中,AC边上有一点D,使得,将沿BD翻折得,此时A D//BC,则= 度.
8.正边形的每个内角都是,这个正边形的对角线条数为 条.
9.如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2= 度.
10.如图,小新从A点出发,沿直线前进50米后向左转30°,再沿直线前进50米,又向左转30°,…照这样下去,小新第一次回到出发地A点时,一共走了 米.
11.如图,在中,点分别在上,,,、相交于点.若的面积为,则四边形的面积是 .(用含的代数式表示)
三、计算题
12.已知一个多边形的内角和比外角和的4倍还多,求这个多边形的边数.
13.如图,直线a∥b,△DCB中,AB与DC垂直,点A在线段BC上,直线b经过点C.若∠1=73°﹣∠B,求∠2的度数.
四、解答题
14.如图,,平分,,,求的度数.
15.如图,在中,,,平分交于点M,求证:.
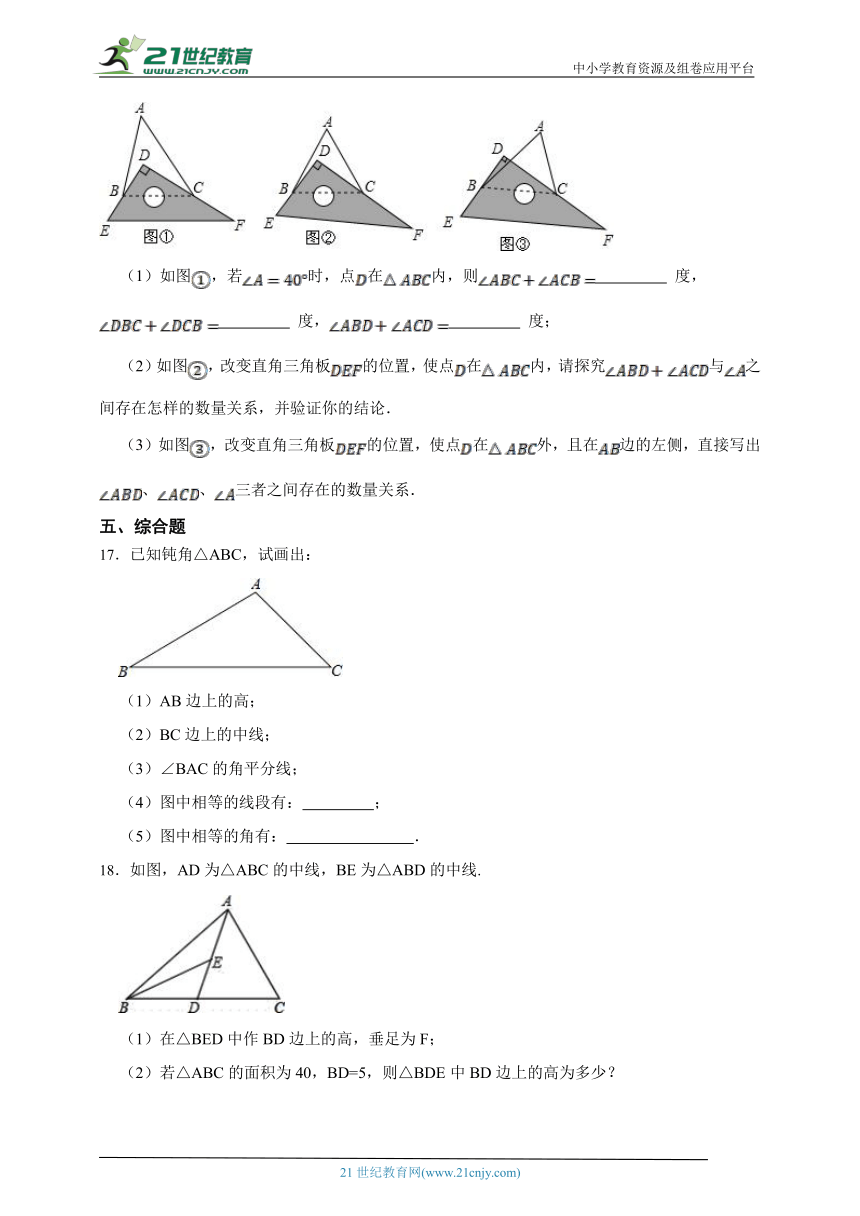
16. 将一块直角三角板放置在锐角上,使得该三角板的两条直角边、恰好分别经过点、.
(1)如图,若时,点在内,则 度, 度, 度;
(2)如图,改变直角三角板的位置,使点在内,请探究与之间存在怎样的数量关系,并验证你的结论.
(3)如图,改变直角三角板的位置,使点在外,且在边的左侧,直接写出、、三者之间存在的数量关系.
五、综合题
17.已知钝角△ABC,试画出:
(1)AB边上的高;
(2)BC边上的中线;
(3)∠BAC的角平分线;
(4)图中相等的线段有: ;
(5)图中相等的角有: .
18.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)在△BED中作BD边上的高,垂足为F;
(2)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?
19.如图,在平面直角坐标系中,已知 ,其中a,b满足
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点C(-2,m),请用含m的式子表示△ABC的面积;
(3)在⑵条件下,当 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
六、实践探究题
20.【问题呈现】
如图①,已知线段,相交于点,连结,,我们把形如这样的图形称为“字型”.
(1)证明:.
(2)【问题探究】
继续探究,如图②,、分别平分、,、交于点,求与、之间的数量关系.为了研究这一问题,尝试代入、的值求的值,得到下面几组对应值:
表中 ,猜想得到与、的数量关系为 ;
(3)证明()中猜想得到的与、的数量关系;
(单位:度)
(单位:度)
(单位:度)
答案解析部分
1.【答案】B
【知识点】三角形的稳定性
2.【答案】B
【知识点】三角形三边关系
3.【答案】C
【知识点】三角形的稳定性
4.【答案】A
【知识点】多边形内角与外角
5.【答案】C
【知识点】三角形的角平分线、中线和高
6.【答案】3
【知识点】三角形的角平分线、中线和高
7.【答案】75
【知识点】三角形内角和定理;内错角的概念
8.【答案】9
【知识点】多边形的对角线
9.【答案】270
【知识点】三角形内角和定理;多边形内角与外角
10.【答案】600
【知识点】多边形内角与外角
11.【答案】
【知识点】三角形的面积
12.【答案】11
【知识点】多边形内角与外角
13.【答案】解∵∠1=73°﹣∠B
∴∠1+∠B=73°,
又由三角形外角性质可得:∠3=∠1+∠B,
∴∠3=73°,
∵AB与DC垂直
∴∠ACD=90°,
∵a∥b
∴∠3+∠2+∠ACD=180°,
∴∠2=180°﹣∠3﹣∠ACD,
=180°﹣73°﹣90°,
=17°.
【知识点】平行线的性质;三角形内角和定理
14.【答案】的度数为
【知识点】三角形内角和定理
15.【答案】证明:∵,,
∴,
∵平分,
∴,
∴,
∴.
【知识点】三角形内角和定理;角平分线的概念
16.【答案】(1)140;90;50
(2)解:与之间的数量关系为:证明如下:
在中,
在中,
.
.
(3).
【知识点】角的运算;三角形内角和定理
17.【答案】(1)解:如图,CD为所作
(2)解:如图,AE为所作
(3)解:如图,AF为所作;
(4)BE=CE
(5)∠BAF=∠CAF
【知识点】三角形的角平分线、中线和高
18.【答案】(1)如图所示,EF即为所求;
(2)∵AD为△ABC的中线,BE为△ABD的中线,
∴S△ABD= S△ABC,S△BDE= S△ABD,
∴S△BDE= × S△ABC= S△ABC,
∵△ABC的面积为40,
∴S△BDE= ×40=10,
∵BD=5,
∴ ×5 EF=10,解得EF=4.
【知识点】三角形的角平分线、中线和高;三角形的面积
19.【答案】(1)-1;3
(2)解:过点M作MN⊥x轴于点N,
∵A(-1,0),B(3,0),
∴AB=1+3=4,
又∵点M(-2,m)在第三象限
∴MN=|m|=-m
∴S△ABM= AB MN= ×4×(-m)=-2m;
(3)解:当m=- 时,M(-2,- )
∴S△ABM=-2×(- )=3,
点P有两种情况:①当点P在y轴正半轴上时,设点p(0,k)
S△BMP=5×( +k)- ×2×( +k)- ×5× - ×3×k= k+ ,
∵S△BMP=S△ABM,
∴ k+ =3,
解得:k=0.3,
∴点P坐标为(0,0.3);
②当点P在y轴负半轴上时,设点p(0,n),
S△BMP=-5n- ×2×(-n- )- ×5× - ×3×(-n)=- n- ,
∵S△BMP=S△ABM,
∴- n- =3,
解得:n=-2.1,
∴点P坐标为(0,-2.1),
故点P的坐标为(0,0.3)或(0,-2.1).
【知识点】三角形的面积;偶次方的非负性;绝对值的非负性;点的坐标与象限的关系
20.【答案】(1)证明:在中,,
在中,,
∵,
∴;
(2);
(3)证明:∵、分别平分、,
∴,
由()得,①,②,
由,得:,
∴,
【知识点】角的运算;三角形内角和定理;对顶角及其性质;角平分线的概念
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【人教版数学八年级上册同步练习】
第十一章三角形综合检测题
一、单选题
1.下面的图形中,具有稳定性的是( )
A. B.
C. D.
2.若三角形的两边长分别为和,则下列长度的线段能作为第三边的是( )
A. B. C. D.
3.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A.三角形三个内角和等于180° B.直角三角形的两个锐角互余
C.三角形具有稳定性 D.两点之间,线段最短
4.如图,∠1,∠2,∠3,∠4,∠5是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=75°,则∠AED的度数是( )
A.120° B.110° C.115° D.100°
5.如图, 是 的中线, 比 长 ,若 的周长为 ,则△ 的周长为( )
A. B. C. D.
二、填空题
6.如图,在中,点、分别是、的中点,,则= .
7.如图所示,中,AC边上有一点D,使得,将沿BD翻折得,此时A D//BC,则= 度.
8.正边形的每个内角都是,这个正边形的对角线条数为 条.
9.如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2= 度.
10.如图,小新从A点出发,沿直线前进50米后向左转30°,再沿直线前进50米,又向左转30°,…照这样下去,小新第一次回到出发地A点时,一共走了 米.
11.如图,在中,点分别在上,,,、相交于点.若的面积为,则四边形的面积是 .(用含的代数式表示)
三、计算题
12.已知一个多边形的内角和比外角和的4倍还多,求这个多边形的边数.
13.如图,直线a∥b,△DCB中,AB与DC垂直,点A在线段BC上,直线b经过点C.若∠1=73°﹣∠B,求∠2的度数.
四、解答题
14.如图,,平分,,,求的度数.
15.如图,在中,,,平分交于点M,求证:.
16. 将一块直角三角板放置在锐角上,使得该三角板的两条直角边、恰好分别经过点、.
(1)如图,若时,点在内,则 度, 度, 度;
(2)如图,改变直角三角板的位置,使点在内,请探究与之间存在怎样的数量关系,并验证你的结论.
(3)如图,改变直角三角板的位置,使点在外,且在边的左侧,直接写出、、三者之间存在的数量关系.
五、综合题
17.已知钝角△ABC,试画出:
(1)AB边上的高;
(2)BC边上的中线;
(3)∠BAC的角平分线;
(4)图中相等的线段有: ;
(5)图中相等的角有: .
18.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)在△BED中作BD边上的高,垂足为F;
(2)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?
19.如图,在平面直角坐标系中,已知 ,其中a,b满足
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点C(-2,m),请用含m的式子表示△ABC的面积;
(3)在⑵条件下,当 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
六、实践探究题
20.【问题呈现】
如图①,已知线段,相交于点,连结,,我们把形如这样的图形称为“字型”.
(1)证明:.
(2)【问题探究】
继续探究,如图②,、分别平分、,、交于点,求与、之间的数量关系.为了研究这一问题,尝试代入、的值求的值,得到下面几组对应值:
表中 ,猜想得到与、的数量关系为 ;
(3)证明()中猜想得到的与、的数量关系;
(单位:度)
(单位:度)
(单位:度)
答案解析部分
1.【答案】B
【知识点】三角形的稳定性
2.【答案】B
【知识点】三角形三边关系
3.【答案】C
【知识点】三角形的稳定性
4.【答案】A
【知识点】多边形内角与外角
5.【答案】C
【知识点】三角形的角平分线、中线和高
6.【答案】3
【知识点】三角形的角平分线、中线和高
7.【答案】75
【知识点】三角形内角和定理;内错角的概念
8.【答案】9
【知识点】多边形的对角线
9.【答案】270
【知识点】三角形内角和定理;多边形内角与外角
10.【答案】600
【知识点】多边形内角与外角
11.【答案】
【知识点】三角形的面积
12.【答案】11
【知识点】多边形内角与外角
13.【答案】解∵∠1=73°﹣∠B
∴∠1+∠B=73°,
又由三角形外角性质可得:∠3=∠1+∠B,
∴∠3=73°,
∵AB与DC垂直
∴∠ACD=90°,
∵a∥b
∴∠3+∠2+∠ACD=180°,
∴∠2=180°﹣∠3﹣∠ACD,
=180°﹣73°﹣90°,
=17°.
【知识点】平行线的性质;三角形内角和定理
14.【答案】的度数为
【知识点】三角形内角和定理
15.【答案】证明:∵,,
∴,
∵平分,
∴,
∴,
∴.
【知识点】三角形内角和定理;角平分线的概念
16.【答案】(1)140;90;50
(2)解:与之间的数量关系为:证明如下:
在中,
在中,
.
.
(3).
【知识点】角的运算;三角形内角和定理
17.【答案】(1)解:如图,CD为所作
(2)解:如图,AE为所作
(3)解:如图,AF为所作;
(4)BE=CE
(5)∠BAF=∠CAF
【知识点】三角形的角平分线、中线和高
18.【答案】(1)如图所示,EF即为所求;
(2)∵AD为△ABC的中线,BE为△ABD的中线,
∴S△ABD= S△ABC,S△BDE= S△ABD,
∴S△BDE= × S△ABC= S△ABC,
∵△ABC的面积为40,
∴S△BDE= ×40=10,
∵BD=5,
∴ ×5 EF=10,解得EF=4.
【知识点】三角形的角平分线、中线和高;三角形的面积
19.【答案】(1)-1;3
(2)解:过点M作MN⊥x轴于点N,
∵A(-1,0),B(3,0),
∴AB=1+3=4,
又∵点M(-2,m)在第三象限
∴MN=|m|=-m
∴S△ABM= AB MN= ×4×(-m)=-2m;
(3)解:当m=- 时,M(-2,- )
∴S△ABM=-2×(- )=3,
点P有两种情况:①当点P在y轴正半轴上时,设点p(0,k)
S△BMP=5×( +k)- ×2×( +k)- ×5× - ×3×k= k+ ,
∵S△BMP=S△ABM,
∴ k+ =3,
解得:k=0.3,
∴点P坐标为(0,0.3);
②当点P在y轴负半轴上时,设点p(0,n),
S△BMP=-5n- ×2×(-n- )- ×5× - ×3×(-n)=- n- ,
∵S△BMP=S△ABM,
∴- n- =3,
解得:n=-2.1,
∴点P坐标为(0,-2.1),
故点P的坐标为(0,0.3)或(0,-2.1).
【知识点】三角形的面积;偶次方的非负性;绝对值的非负性;点的坐标与象限的关系
20.【答案】(1)证明:在中,,
在中,,
∵,
∴;
(2);
(3)证明:∵、分别平分、,
∴,
由()得,①,②,
由,得:,
∴,
【知识点】角的运算;三角形内角和定理;对顶角及其性质;角平分线的概念
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
