2015-2016学年八年级数学(下)第18章 平行四边形检测题(附答案解析)
文档属性
| 名称 | 2015-2016学年八年级数学(下)第18章 平行四边形检测题(附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 967.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-29 08:17:11 | ||
图片预览



文档简介
第18章 平行四边形检测题
(时间:90分钟,满分:100分)
一、选择题(每小题3分,共27分)
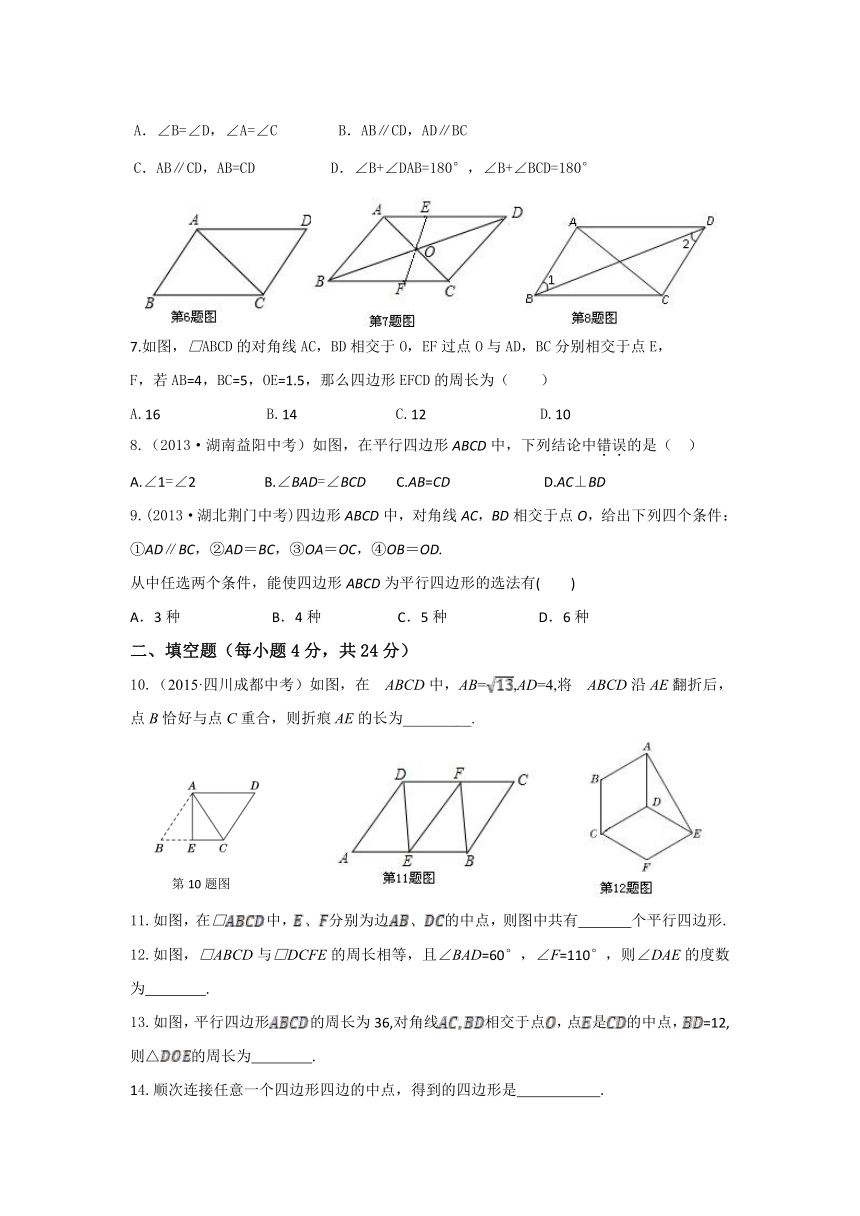
1.(2015·广东广州中考)下列命题中,真命题的个数是( )
①对角线互相平分的四边形是平行四边形.
②两组对角分别相等的四边形是平行四边形.
③一组对边平行,另一组对边相等的四边形是平行四边形.
A.3个 B.2个 C.1个 D.0个
2.如图,在平行四边形中,,,的垂直平分线交于点,则△
的周长是( )
A.6 B.8 C.9 D.10
3.如图,已知□的周长是,△ABC的周长是,则的长为( )
A. B. C. D.
4.(2013·哈尔滨中考)如图,在□ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,
且AE=3,则AB的长为( )
A.4 B.3 C. D.2
5.(2013·杭州中考)如图,在□ABCD中,下列结论一定正确的是( )
A.AC⊥BD B.∠A+∠B=180°
C.AB=AD D.∠A≠∠C
6.如图,由下面条件不能判断四边形ABCD是平行四边形的是( )
A.∠B=∠D,∠A=∠C B.AB∥CD,AD∥BCC.AB∥CD,AB=CD D.∠B+∠DAB=180°,∠B+∠BCD=180°
7.如图,□ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于点E,
F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为( )
A.16 B.14 C.12 D.10
8.(2013·湖南益阳中考)如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD C.AB=CD D.AC⊥BD
9.(2013·湖北荆门中考)四边形ABCD中,对角线AC,BD相交于点O,给出下列四个条件:
①AD∥BC,②AD=BC,③OA=OC,④OB=OD.
从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
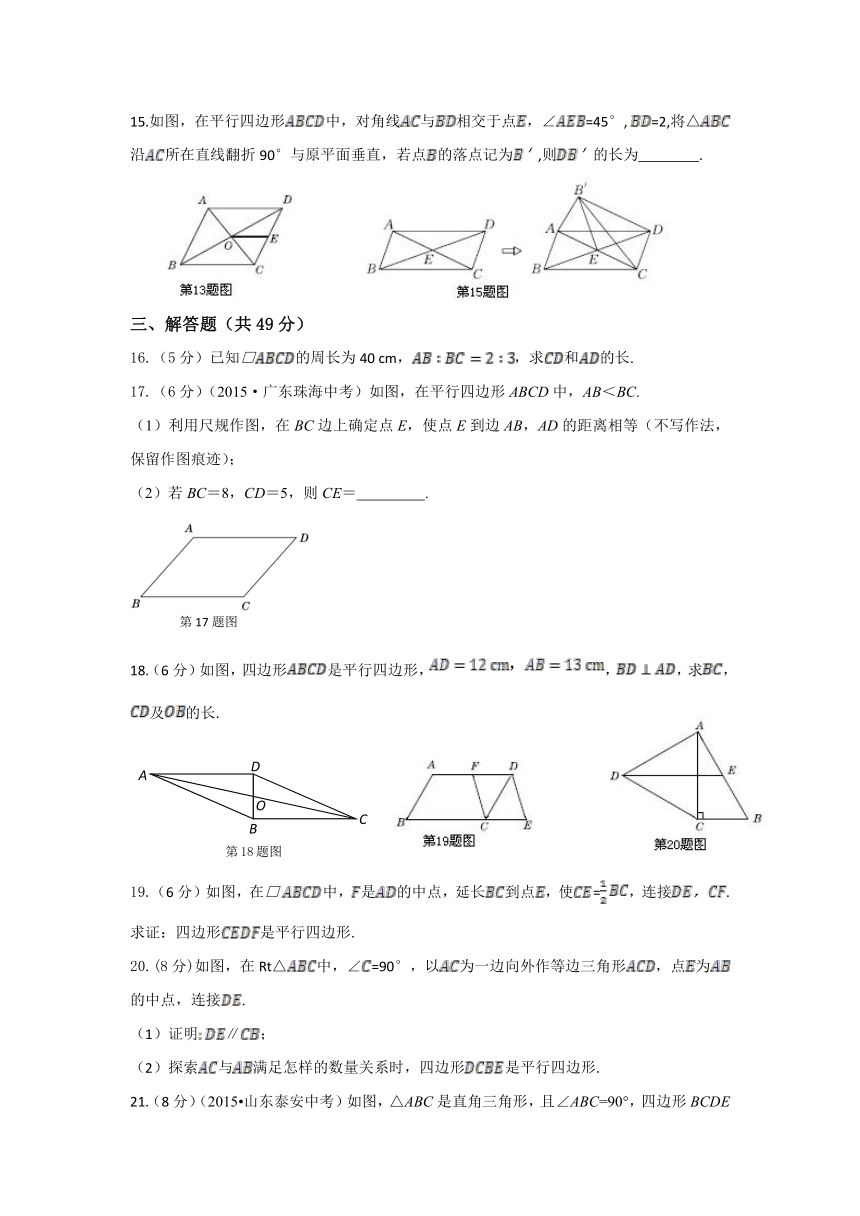
二、填空题(每小题4分,共24分)
10.(2015·四川成都中考)如图,在?ABCD中,AB=,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为_________.
11.如图,在□中,分别为边的中点,则图中共有 个平行四边形.
12.如图,□ABCD与□DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为 .
13.如图,平行四边形的周长为36,对角线相交于点,点是的中点,=12,则△的周长为 .
14.顺次连接任意一个四边形四边的中点,得到的四边形是 .
15.如图,在平行四边形中,对角线与相交于点,∠=45°,=2,将△沿所在直线翻折90°与原平面垂直,若点的落点记为,则的长为 .
三、解答题(共49分)
16.(5分)已知□的周长为40 cm,,求和的长.
17.(6分)(2015·广东珠海中考)如图,在平行四边形ABCD中,AB<BC.
(1)利用尺规作图,在BC边上确定点E,使点E到边AB,AD的距离相等(不写作法,保留作图痕迹);
(2)若BC=8,CD=5,则CE= .
18.(6分)如图,四边形是平行四边形,,,求,及的长.
19.(6分)如图,在□中,是的中点,延长到点,使=,连接.
求证:四边形是平行四边形.
20.(8分)如图,在Rt△中,∠=90°,以为一边向外作等边三角形,点为的中点,连接.
(1)证明∥;
(2)探索与满足怎样的数量关系时,四边形是平行四边形.
21.(8分)(2015 山东泰安中考)如图,△ABC是直角三角形,且∠ABC=90°,四边形BCDE是平行四边形,E为AC中点,BD平分∠ABC,点F在AB上,且BF=BC.
求证:(1)DF=AE;
(2)DF⊥AC.
22.(10分) (2013·兰州中考)如图 (1),在△中,∠=90°,∠=30°,=8.以为边,在△外作等边△,是的中点,连接并延长交于点.
(1)求证:四边形是平行四边形.
(2)如图(2),将图(1)中的四边形折叠,使点与点重合,折痕为,求的长.
第18章 平行四边形检测题参考答案
1.B 解析:因为对角线互相平分的四边形是平行四边形,所以①正确;因为两组对角分别相等的四边形是平行四边形,所以②正确;因为一组对边平行且相等的四边形是平行四边形,所以③错误.故正确的是①②.
2.B 解析:在平行四边形中,
因为的垂直平分线交于点,所以
所以△的周长为
3.D 解析:因为□的周长是28 cm,所以 .
因为△的周长是,所以 .
4.B 解析:∵ CE平分∠BCD,∴ ∠BCE=∠DCE.
∵ 四边形ABCD是平行四边形,∴ AD∥BC.∴ ∠DEC=∠BCE.
∴ ∠DCE=∠DEC.∴ CD=DE. ∴ AD=2AB=2CD=2DE.
∴ DE=AE=3.∴ AB=CD=DE=3.
5.B 解析:平行四边形的对角线互相平分但不一定垂直,所以选项A错误;平行四边形的
邻角互补,所以选项B正确;平行四边形的对边相等但邻边不一定相等,所以选项C错误;
平行四边形的对角相等,所以∠A=∠C,所以选项D错误.
6.A 解析:对角相等不可以证明四边形是平行四边形,故A选项错误;根据两组对边分别平行的四边形是平行四边形可以证明四边形ABCD为平行四边形,故B选项正确;有一组对边平行且相等的四边形是平行四边形可以证明四边形ABCD为平行四边形,故C选项正确;根据∠B +∠DAB=180°可以证明AD∥BC,根据∠B+∠BCD=180°可以证明AB∥CD,根据两组对边分别平行的四边形是平行四边形可以证明四边形ABCD为平行四边形,故D选项正确.
7.C 解析:∵ 四边形ABCD是平行四边形,
∴ CD=AB=4,AD=BC=5,OA=OC,AD∥BC,∴ ∠EAO=∠FCO,∠AEO=∠CFO.
在△AOE和△COF中, ∠EAO=∠FCO ,∠AEO =∠CFO, OA=OC ,
∴ △AOE≌△COF,∴ OF=OE=1.5,CF=AE.
故四边形EFCD的周长为CD+EF+ED+FC=CD+EF+AE+ED=CD+EF+AD=12.故选C.
8.D 解析:根据平行四边形的性质可知D是错误的.
9.B 解析:从四个条件中任选两个,共有6种选法.若选②③或选②④,则不能使四边形ABCD是平行四边形.其他4种选法,即选①②或①③或①④或③④,则均能使四边形ABCD为平行四边形.故选B.
10.3 解析:点B恰好与点C重合,且四边形ABCD是平行四边形,根据翻折的性质,得AE⊥BC,BE=CE=2.在Rt△ABE中,由勾股定理得AE===3.
11.4 解析:因为在□ABCD中,E、F分别为边AB、DC的中点,所以 .
又AB∥CD,所以四边形AEFD,CFEB,DFBE都是平行四边形,再加上□ABCD本身,共有4
个平行四边形,故答案为4.
12.25° 解析:因为□ABCD与□DCFE的周长相等,且DC为公共边,
所以AD=DE,所以∠DAE=∠DEA.
因为AB∥DC,DC∥EF,所以AB∥EF,所以∠BAE+∠FEA=180°,
即∠BAD+∠DAE+∠FED+∠DEA=180°.
因为DE∥CF,∠F=110°,所以∠FED+∠F=180°,则∠FED=70°.
因为∠BAD=60°,所以60°+70°+2∠DAE=180°,所以∠DAE=25°.
13.15 解析:本题综合考查了平行四边形的性质以及三角形的中位线定理.
∵ 点分别是的中点,∴ 是△的一条中位线,∴ ,
∴ △的周长==6
=□的周长+6=15.
14.平行四边形
15. 解析:∵ 四边形是平行四边形,
∴==1.由折叠知=1,∠=90°.
在Rt△中,=.
点拨:平行四边形的两条对角线互相平分.
16.解: 因为四边形是平行四边形,所以,.
设 cm, cm,
又因为平行四边形的周长为40 cm,
所以,解得,
所以 , .
17.分析:(1)由于点E到AB,AD的距离相等,所以点E在∠BAD的平分线上,因此
∠BAD的平分线与BC的交点即为所求的点E.
(2)∵ AE平分∠BAD,∴ ∠BAE=∠DAE.
∵ AD∥BC,
∴ ∠DAE=∠BEA,∴ ∠BAE=∠BEA.
又∵ AB=5,∴ BE=AB=5.
∴ CE=BC-BE=8-5=3.
解:(1)如图:
(2)3
18.解:因为四边形ABCD是平行四边形,
所以,,.
因为,所以,
所以.
19.分析:可根据“一组对边平行且相等的四边形是平行四边形”进行判定.
证明:∵ 四边形是平行四边形,
∴ ∥, .
∵ 的中点,∴
∵ QUOTE QUOTE ,∴ .
∵ QUOTE ∥,∴ 四边形是平行四边形.
20.(1)证明:如图,连接,
∵为Rt△的斜边的中点,
∴ .
∵ △是等边三角形,
∴ .
在△和△中,
∴ △≌△(SSS).
∴ ∠ADE=∠CDE =30°.
∵ ∠DCB=∠ACB+ ∠ACD =90°+60°=150°,
∴ ∠EDC+∠DCB =180°,∴ QUOTE ∥.
(2)解:∵ ∠=150°,
若四边形是平行四边形,则DC∥BE, ∠DCB+∠B=180°,∴∠B =30°.
在Rt△中,∵ 在直角三角形中,30°角所对的直角边等于斜边的一半,
∴ .
∴ 当时,四边形是平行四边形.
点拨:(1)利用直角三角形中,斜边上的中线等于斜边的一半进行转化,线段相等是证明两个三角形全等的关键.
(2)对于条件探索性问题常通过逆向思维的方式得到解决.
21. 证法一:(1)如图(1),延长DE交AB于点G,连接AD.
∵ ED∥BC,E是AC的中点,∠ABC=90°,
∴ AG=BG,DG⊥AB,∴ AD=BD.
∵ BD平分∠ABC,
∴ ∠ABD=45°,∠BAD=45°,∠BDG=∠ADG=45°.
∵ 四边形BCDE是平行四边形,∴ ED=BC.
又∵ BF=BC,∴ BF=DE. ∴ △AED≌△DFB,
∴ AE=DF.
(2)∵ △AED≌△DFB,∴ ∠AED=∠DFB,
∴ ∠DFG=∠DEC.
∵ ∠DFG与∠FDG互余,∴ ∠DEC与∠FDG互余.
∴ DF⊥AC.
证法二:(1)∵ △ABC是直角三角形,且∠ABC=90°,E为AC的中点,
∴ AE=BE.
∵ 四边形BCDE是平行四边形,∴ BE=DC.
∵ BD平分∠ABC,∴ ∠ABD=∠DBC.
又∵ BF=BC,BD=BD,
∴ △DFB≌△DCB.∴ DF=DC. ∴ DF=AE.
(2)由(1)得△DFB≌△DCB,
∴ ∠DFB=∠DCB.
延长DE交AB于点G,如图(2),
∵ 四边形BCDE是平行四边形,∴ ∠DCB=∠DEB.
而∠DEB+∠GEB=180°,∠AFD+∠DFB=180°,
∴ ∠AFD=∠GEB.
∵ ∠ABC=90°,DE∥BC,∴ DG⊥AB.
又AE=BE,∴ ∠DEC=∠AEG=∠GEB=∠AFD.
∵ ∠AFD+∠GDF=90°,∴ ∠DEC+∠GDF=90°.∴ DF⊥AC.
22.分析:(1)根据∠=30°,△为等边三角形,得∠=90°,
根据∠=90°,得∥.
由点为的中点,得,
所以∠DAO=∠DOA =30°,所以在Rt△中,
∠=60°,所以∠AEO =∠C ,所以∥,故四边形是平行四边形.
(2)设,由题意可知△≌△
在Rt△中运用勾股定理求出的长.
(1)证明:在Rt△中,
∵为的中点,∴ ,∴ ∠DAO=∠DOA =30°.
又∵ △为等边三角形,
∴ ∠BCO=∠BOC=60°,∴ ∠EOA =90°,∴ ∠AEO =60°.
∴ ∠BCO=∠AEO,∴ ∥.
∵ ∠BAO=∠COA=90°,
∴ ∥,∴ 四边形是平行四边形.
(2)解:设,由折叠可知,
在Rt△中,
∵ ∠OAB=90°,∠ =30°,=8,
∴ AB=4,OA=4 .
在Rt△中,,
∴,解得 =1,∴ =1.
第3题图
A
B
C
D
第2题图
A
B
C
D
E
第10题图
第17题图
A
B
C
O
D
第18题图
第21题图
第21题图(1)
第21题图(2)
(时间:90分钟,满分:100分)
一、选择题(每小题3分,共27分)
1.(2015·广东广州中考)下列命题中,真命题的个数是( )
①对角线互相平分的四边形是平行四边形.
②两组对角分别相等的四边形是平行四边形.
③一组对边平行,另一组对边相等的四边形是平行四边形.
A.3个 B.2个 C.1个 D.0个
2.如图,在平行四边形中,,,的垂直平分线交于点,则△
的周长是( )
A.6 B.8 C.9 D.10
3.如图,已知□的周长是,△ABC的周长是,则的长为( )
A. B. C. D.
4.(2013·哈尔滨中考)如图,在□ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,
且AE=3,则AB的长为( )
A.4 B.3 C. D.2
5.(2013·杭州中考)如图,在□ABCD中,下列结论一定正确的是( )
A.AC⊥BD B.∠A+∠B=180°
C.AB=AD D.∠A≠∠C
6.如图,由下面条件不能判断四边形ABCD是平行四边形的是( )
A.∠B=∠D,∠A=∠C B.AB∥CD,AD∥BCC.AB∥CD,AB=CD D.∠B+∠DAB=180°,∠B+∠BCD=180°
7.如图,□ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于点E,
F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为( )
A.16 B.14 C.12 D.10
8.(2013·湖南益阳中考)如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD C.AB=CD D.AC⊥BD
9.(2013·湖北荆门中考)四边形ABCD中,对角线AC,BD相交于点O,给出下列四个条件:
①AD∥BC,②AD=BC,③OA=OC,④OB=OD.
从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
二、填空题(每小题4分,共24分)
10.(2015·四川成都中考)如图,在?ABCD中,AB=,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为_________.
11.如图,在□中,分别为边的中点,则图中共有 个平行四边形.
12.如图,□ABCD与□DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为 .
13.如图,平行四边形的周长为36,对角线相交于点,点是的中点,=12,则△的周长为 .
14.顺次连接任意一个四边形四边的中点,得到的四边形是 .
15.如图,在平行四边形中,对角线与相交于点,∠=45°,=2,将△沿所在直线翻折90°与原平面垂直,若点的落点记为,则的长为 .
三、解答题(共49分)
16.(5分)已知□的周长为40 cm,,求和的长.
17.(6分)(2015·广东珠海中考)如图,在平行四边形ABCD中,AB<BC.
(1)利用尺规作图,在BC边上确定点E,使点E到边AB,AD的距离相等(不写作法,保留作图痕迹);
(2)若BC=8,CD=5,则CE= .
18.(6分)如图,四边形是平行四边形,,,求,及的长.
19.(6分)如图,在□中,是的中点,延长到点,使=,连接.
求证:四边形是平行四边形.
20.(8分)如图,在Rt△中,∠=90°,以为一边向外作等边三角形,点为的中点,连接.
(1)证明∥;
(2)探索与满足怎样的数量关系时,四边形是平行四边形.
21.(8分)(2015 山东泰安中考)如图,△ABC是直角三角形,且∠ABC=90°,四边形BCDE是平行四边形,E为AC中点,BD平分∠ABC,点F在AB上,且BF=BC.
求证:(1)DF=AE;
(2)DF⊥AC.
22.(10分) (2013·兰州中考)如图 (1),在△中,∠=90°,∠=30°,=8.以为边,在△外作等边△,是的中点,连接并延长交于点.
(1)求证:四边形是平行四边形.
(2)如图(2),将图(1)中的四边形折叠,使点与点重合,折痕为,求的长.
第18章 平行四边形检测题参考答案
1.B 解析:因为对角线互相平分的四边形是平行四边形,所以①正确;因为两组对角分别相等的四边形是平行四边形,所以②正确;因为一组对边平行且相等的四边形是平行四边形,所以③错误.故正确的是①②.
2.B 解析:在平行四边形中,
因为的垂直平分线交于点,所以
所以△的周长为
3.D 解析:因为□的周长是28 cm,所以 .
因为△的周长是,所以 .
4.B 解析:∵ CE平分∠BCD,∴ ∠BCE=∠DCE.
∵ 四边形ABCD是平行四边形,∴ AD∥BC.∴ ∠DEC=∠BCE.
∴ ∠DCE=∠DEC.∴ CD=DE. ∴ AD=2AB=2CD=2DE.
∴ DE=AE=3.∴ AB=CD=DE=3.
5.B 解析:平行四边形的对角线互相平分但不一定垂直,所以选项A错误;平行四边形的
邻角互补,所以选项B正确;平行四边形的对边相等但邻边不一定相等,所以选项C错误;
平行四边形的对角相等,所以∠A=∠C,所以选项D错误.
6.A 解析:对角相等不可以证明四边形是平行四边形,故A选项错误;根据两组对边分别平行的四边形是平行四边形可以证明四边形ABCD为平行四边形,故B选项正确;有一组对边平行且相等的四边形是平行四边形可以证明四边形ABCD为平行四边形,故C选项正确;根据∠B +∠DAB=180°可以证明AD∥BC,根据∠B+∠BCD=180°可以证明AB∥CD,根据两组对边分别平行的四边形是平行四边形可以证明四边形ABCD为平行四边形,故D选项正确.
7.C 解析:∵ 四边形ABCD是平行四边形,
∴ CD=AB=4,AD=BC=5,OA=OC,AD∥BC,∴ ∠EAO=∠FCO,∠AEO=∠CFO.
在△AOE和△COF中, ∠EAO=∠FCO ,∠AEO =∠CFO, OA=OC ,
∴ △AOE≌△COF,∴ OF=OE=1.5,CF=AE.
故四边形EFCD的周长为CD+EF+ED+FC=CD+EF+AE+ED=CD+EF+AD=12.故选C.
8.D 解析:根据平行四边形的性质可知D是错误的.
9.B 解析:从四个条件中任选两个,共有6种选法.若选②③或选②④,则不能使四边形ABCD是平行四边形.其他4种选法,即选①②或①③或①④或③④,则均能使四边形ABCD为平行四边形.故选B.
10.3 解析:点B恰好与点C重合,且四边形ABCD是平行四边形,根据翻折的性质,得AE⊥BC,BE=CE=2.在Rt△ABE中,由勾股定理得AE===3.
11.4 解析:因为在□ABCD中,E、F分别为边AB、DC的中点,所以 .
又AB∥CD,所以四边形AEFD,CFEB,DFBE都是平行四边形,再加上□ABCD本身,共有4
个平行四边形,故答案为4.
12.25° 解析:因为□ABCD与□DCFE的周长相等,且DC为公共边,
所以AD=DE,所以∠DAE=∠DEA.
因为AB∥DC,DC∥EF,所以AB∥EF,所以∠BAE+∠FEA=180°,
即∠BAD+∠DAE+∠FED+∠DEA=180°.
因为DE∥CF,∠F=110°,所以∠FED+∠F=180°,则∠FED=70°.
因为∠BAD=60°,所以60°+70°+2∠DAE=180°,所以∠DAE=25°.
13.15 解析:本题综合考查了平行四边形的性质以及三角形的中位线定理.
∵ 点分别是的中点,∴ 是△的一条中位线,∴ ,
∴ △的周长==6
=□的周长+6=15.
14.平行四边形
15. 解析:∵ 四边形是平行四边形,
∴==1.由折叠知=1,∠=90°.
在Rt△中,=.
点拨:平行四边形的两条对角线互相平分.
16.解: 因为四边形是平行四边形,所以,.
设 cm, cm,
又因为平行四边形的周长为40 cm,
所以,解得,
所以 , .
17.分析:(1)由于点E到AB,AD的距离相等,所以点E在∠BAD的平分线上,因此
∠BAD的平分线与BC的交点即为所求的点E.
(2)∵ AE平分∠BAD,∴ ∠BAE=∠DAE.
∵ AD∥BC,
∴ ∠DAE=∠BEA,∴ ∠BAE=∠BEA.
又∵ AB=5,∴ BE=AB=5.
∴ CE=BC-BE=8-5=3.
解:(1)如图:
(2)3
18.解:因为四边形ABCD是平行四边形,
所以,,.
因为,所以,
所以.
19.分析:可根据“一组对边平行且相等的四边形是平行四边形”进行判定.
证明:∵ 四边形是平行四边形,
∴ ∥, .
∵ 的中点,∴
∵ QUOTE QUOTE ,∴ .
∵ QUOTE ∥,∴ 四边形是平行四边形.
20.(1)证明:如图,连接,
∵为Rt△的斜边的中点,
∴ .
∵ △是等边三角形,
∴ .
在△和△中,
∴ △≌△(SSS).
∴ ∠ADE=∠CDE =30°.
∵ ∠DCB=∠ACB+ ∠ACD =90°+60°=150°,
∴ ∠EDC+∠DCB =180°,∴ QUOTE ∥.
(2)解:∵ ∠=150°,
若四边形是平行四边形,则DC∥BE, ∠DCB+∠B=180°,∴∠B =30°.
在Rt△中,∵ 在直角三角形中,30°角所对的直角边等于斜边的一半,
∴ .
∴ 当时,四边形是平行四边形.
点拨:(1)利用直角三角形中,斜边上的中线等于斜边的一半进行转化,线段相等是证明两个三角形全等的关键.
(2)对于条件探索性问题常通过逆向思维的方式得到解决.
21. 证法一:(1)如图(1),延长DE交AB于点G,连接AD.
∵ ED∥BC,E是AC的中点,∠ABC=90°,
∴ AG=BG,DG⊥AB,∴ AD=BD.
∵ BD平分∠ABC,
∴ ∠ABD=45°,∠BAD=45°,∠BDG=∠ADG=45°.
∵ 四边形BCDE是平行四边形,∴ ED=BC.
又∵ BF=BC,∴ BF=DE. ∴ △AED≌△DFB,
∴ AE=DF.
(2)∵ △AED≌△DFB,∴ ∠AED=∠DFB,
∴ ∠DFG=∠DEC.
∵ ∠DFG与∠FDG互余,∴ ∠DEC与∠FDG互余.
∴ DF⊥AC.
证法二:(1)∵ △ABC是直角三角形,且∠ABC=90°,E为AC的中点,
∴ AE=BE.
∵ 四边形BCDE是平行四边形,∴ BE=DC.
∵ BD平分∠ABC,∴ ∠ABD=∠DBC.
又∵ BF=BC,BD=BD,
∴ △DFB≌△DCB.∴ DF=DC. ∴ DF=AE.
(2)由(1)得△DFB≌△DCB,
∴ ∠DFB=∠DCB.
延长DE交AB于点G,如图(2),
∵ 四边形BCDE是平行四边形,∴ ∠DCB=∠DEB.
而∠DEB+∠GEB=180°,∠AFD+∠DFB=180°,
∴ ∠AFD=∠GEB.
∵ ∠ABC=90°,DE∥BC,∴ DG⊥AB.
又AE=BE,∴ ∠DEC=∠AEG=∠GEB=∠AFD.
∵ ∠AFD+∠GDF=90°,∴ ∠DEC+∠GDF=90°.∴ DF⊥AC.
22.分析:(1)根据∠=30°,△为等边三角形,得∠=90°,
根据∠=90°,得∥.
由点为的中点,得,
所以∠DAO=∠DOA =30°,所以在Rt△中,
∠=60°,所以∠AEO =∠C ,所以∥,故四边形是平行四边形.
(2)设,由题意可知△≌△
在Rt△中运用勾股定理求出的长.
(1)证明:在Rt△中,
∵为的中点,∴ ,∴ ∠DAO=∠DOA =30°.
又∵ △为等边三角形,
∴ ∠BCO=∠BOC=60°,∴ ∠EOA =90°,∴ ∠AEO =60°.
∴ ∠BCO=∠AEO,∴ ∥.
∵ ∠BAO=∠COA=90°,
∴ ∥,∴ 四边形是平行四边形.
(2)解:设,由折叠可知,
在Rt△中,
∵ ∠OAB=90°,∠ =30°,=8,
∴ AB=4,OA=4 .
在Rt△中,,
∴,解得 =1,∴ =1.
第3题图
A
B
C
D
第2题图
A
B
C
D
E
第10题图
第17题图
A
B
C
O
D
第18题图
第21题图
第21题图(1)
第21题图(2)
