山东省青岛市崂山区2023-2024学年人教版八年级下学期期末数学试卷(无答案)
文档属性
| 名称 | 山东省青岛市崂山区2023-2024学年人教版八年级下学期期末数学试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 332.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-15 17:05:10 | ||
图片预览


文档简介
山东省青岛市崂山区2023-2024学年八年级下学期期末数学试卷
一、选择题(本大题共10小题,每小题3分,满分30分)
1.(3分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.(3分)如果a>b,则下列式子正确的是( )
A.ac2>bc2 B.2a<2b C.a﹣1<b﹣1 D.
3.(3分)随着青岛市地铁线路陆续开通,小明同学上学不再乘坐公交车,改乘地铁,这样他乘坐地铁上学比乘坐公交车上学所需要的时间少了10分钟.已知小明同学家距学校8千米,乘坐地铁平均速度比乘坐公交车平均速度每小时快20千米,若设乘公交车平均速度为x千米每小时,根据题意可列方程为( )
A. B.
C. D.
4.(3分)下列各式从左到右,属于因式分解的是( )
A.(a+b)(a﹣b)=a2﹣b2
B.a2﹣4a+1=a(a﹣4)+1
C.a2﹣6a+9=(a﹣3)2
D.
5.(3分)下列正多边形中,与正三角形同时使用不能进行镶嵌的是( )
A.正六边形 B.正十二边形
C.正八边形 D.正四边形
6.(3分)如图,△ABC绕点A按顺时针方向旋转57°后与△AB'C'重合,连接BB',则∠CAC'=( )
A.45° B.47° C.51° D.57°
7.(3分)如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点.若PA=4,则PQ的长不可能是( )
A.3.9 B.4 C.4.3 D.5.5
8.(3分)某电梯乘载的重量超过1000公斤时会响起警示音,小刚、小明的体重分别为55公斤、70公斤.小刚、小明依序进入电梯,小刚走进后,警示音没响,小明走进后,警示音响起.设两人没进入电梯前已乘载的重量为x公斤,则x满足( )
A.930<x≤970 B.875≤x<945 C.875<x≤945 D.930≤x<970
9.(3分)如图,将一副直角三角板在平行四边形ABCD中作如下摆放,若∠1=30°,那么∠2=( )
A.60° B.75° C.70° D.35°
10.(3分)已知直线y1=kx+b(k>0)与x轴交于点(﹣2,0),直线y2=mx+b(n<0)与x轴交于点(3,0),据此推断不等式kx+b≥mx+b>0的解集为( )
A.﹣2<x<3 B.0<x≤3 C.﹣2≤x<0 D.0≤x<3
二、填空题(本大题共6小题,每小题3分,满分18分)
11.(3分)若分式的值为0,则x的值为 .
12.(3分)如图,在△ABC中,点D是边BC上的一点.若AB=AD=DC,∠BAD=52°,则∠C的度数为 °.
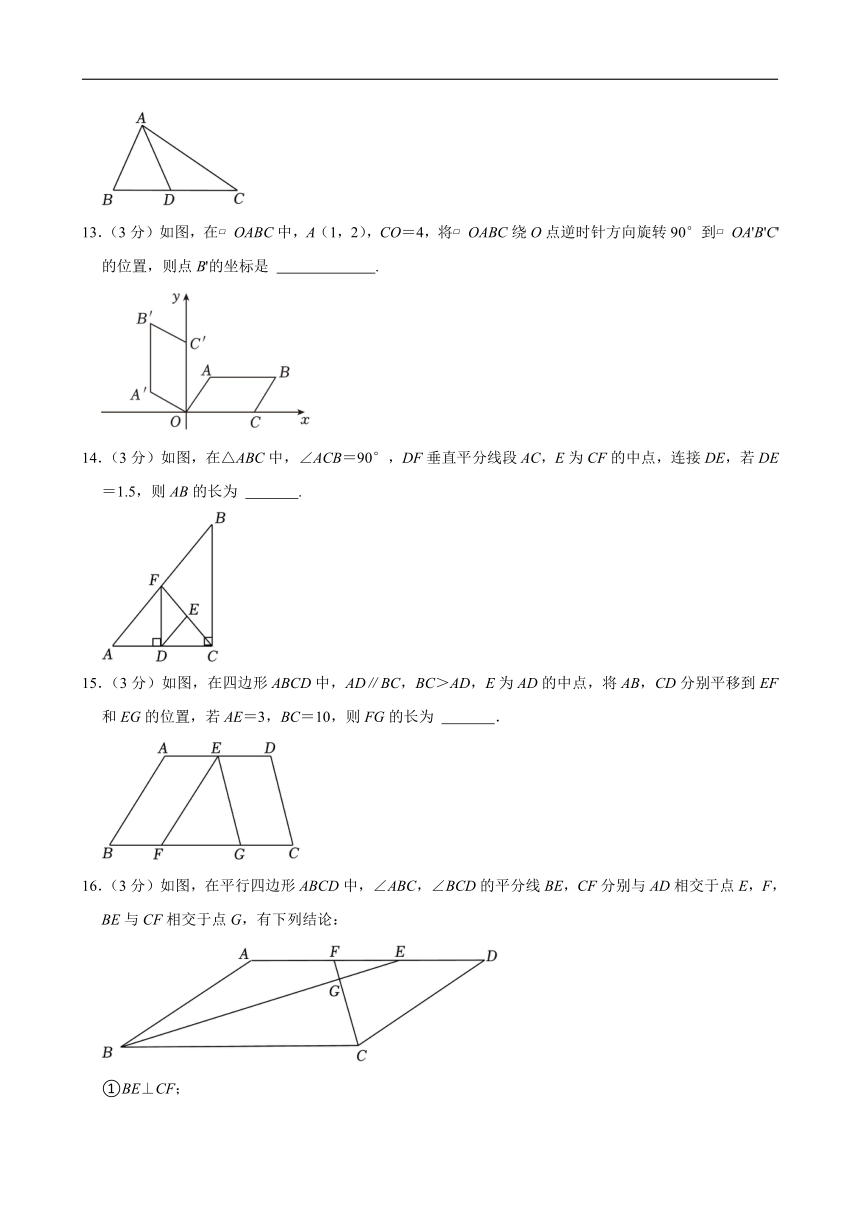
13.(3分)如图,在 OABC中,A(1,2),CO=4,将 OABC绕O点逆时针方向旋转90°到 OA'B'C'的位置,则点B'的坐标是 .
14.(3分)如图,在△ABC中,∠ACB=90°,DF垂直平分线段AC,E为CF的中点,连接DE,若DE=1.5,则AB的长为 .
15.(3分)如图,在四边形ABCD中,AD∥BC,BC>AD,E为AD的中点,将AB,CD分别平移到EF和EG的位置,若AE=3,BC=10,则FG的长为 .
16.(3分)如图,在平行四边形ABCD中,∠ABC,∠BCD的平分线BE,CF分别与AD相交于点E,F,BE与CF相交于点G,有下列结论:
①BE⊥CF;
②AF=DE;
③若连接BF,CE,则S△BFG=S△CEG;
④若,,则BE=4.
其中,正确的结论是 .(填写序号即可)
三、作图题(本大题满分4分)请用直尺、圆规作图,不写作法,但要保留作图痕迹.
17.(4分)已知:∠α,线段a.
求作:等腰△ABC,使得顶角∠A=∠α,底边BC上的中线长为线段a的长度.
四、解答题(本大题共8小题,满分68分)
18.(8分)计算:
(1)解不等式组:,并求出该不等式组的最大整数解;
(2)分解因式:a2﹣2a(b+c)+(b+c)2.
19.(6分)先化简,然后从﹣1,0,1,2四个数中选择一个合适的数代入求值.
20.(6分)某校学生会组织七年级和八年级共50名学生参加环保活动,七年级学生平均每人收集16个废弃塑料瓶、八年级学生平均每人收集24个废弃塑料瓶,请你根据以上信息,设计一个可以用一元一次不等式解决的问题,并给出解决方案.
21.(6分)命题“在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半”.
(1)请依据命题画出图形,并写出已知,求证;
(2)写出证明过程.
22.(8分)在△ABC中,CD是△ABC的中线,E为CD的中点,过点C作CF∥AB与BE的延长线相交于点F.
(1)如图①,连接FD,判断四边形BDFC的形状并证明你的结论;
(2)如图②,连接AF,若∠ABC=90°,∠DCB=30°,求∠AFB的度数.
23.(10分)为落实青岛市促进中小学生全面发展“十个一”项目行动计划,某学校准备购进一批足球和篮球使更多的学生参与这两个体育项目.据了解,某体育用品超市每个足球的价格比篮球的价格贵30元,用2400元购买篮球的数量是用1500元购买足球数量的2倍.
(1)求每个足球和篮球的价格;
(2)学校决定购买足球和篮球共54个,且购买足球的数量不少于篮球的数量的一半,求本次购买最少花费多少钱?
(3)在(2)最少花费方案下,体育用品超市为支持学校体育活动,对足球提供9折优惠,篮球提供7.5折优惠.学校决定将节约下的资金全部用于再次购买足球和篮球(此时按原价购买,可以只购买一种),求再次购买足球和篮球的方案.
24.(12分)如图,在平面直角坐标系中,已知点A(20,0),B(14,8),C(0,8),动点P从原点O出发,沿x轴正方向匀速运动,速度为2cm/s;同时,动点Q从点B出发,沿射线BC方向匀速运动,速度为1cm/s.设运动时间为t(s).
(1)求直线AB的函数关系式;
(2)当t=4时,直线PQ与直线AB交于点D,求点D的坐标;
(3)当t为何值时,以A,B,Q,P为顶点的四边形为平行四边形.
25.(12分)综合实践课上,同学们展开了以“轴对称”为主题的探究活动.
实践操作:
四边形ABCD是平行四边形,AC⊥AD,∠D=45°,在边BC上取一点P,如图①,连接AP,点B关于AP的对称点为点B',连接B′P、B′A.
问题解决:
(1)当B′A与AC重合时,连接BB',AP与BB'有何位置和数量关系,请说明理由;
(2)如图②,当∠BAP=30°时,连接B'C,AP与BB'位置关系为 ,数量关系为 ;
(3)若,∠B'AC=15°时,求线段BP的长.
一、选择题(本大题共10小题,每小题3分,满分30分)
1.(3分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.(3分)如果a>b,则下列式子正确的是( )
A.ac2>bc2 B.2a<2b C.a﹣1<b﹣1 D.
3.(3分)随着青岛市地铁线路陆续开通,小明同学上学不再乘坐公交车,改乘地铁,这样他乘坐地铁上学比乘坐公交车上学所需要的时间少了10分钟.已知小明同学家距学校8千米,乘坐地铁平均速度比乘坐公交车平均速度每小时快20千米,若设乘公交车平均速度为x千米每小时,根据题意可列方程为( )
A. B.
C. D.
4.(3分)下列各式从左到右,属于因式分解的是( )
A.(a+b)(a﹣b)=a2﹣b2
B.a2﹣4a+1=a(a﹣4)+1
C.a2﹣6a+9=(a﹣3)2
D.
5.(3分)下列正多边形中,与正三角形同时使用不能进行镶嵌的是( )
A.正六边形 B.正十二边形
C.正八边形 D.正四边形
6.(3分)如图,△ABC绕点A按顺时针方向旋转57°后与△AB'C'重合,连接BB',则∠CAC'=( )
A.45° B.47° C.51° D.57°
7.(3分)如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点.若PA=4,则PQ的长不可能是( )
A.3.9 B.4 C.4.3 D.5.5
8.(3分)某电梯乘载的重量超过1000公斤时会响起警示音,小刚、小明的体重分别为55公斤、70公斤.小刚、小明依序进入电梯,小刚走进后,警示音没响,小明走进后,警示音响起.设两人没进入电梯前已乘载的重量为x公斤,则x满足( )
A.930<x≤970 B.875≤x<945 C.875<x≤945 D.930≤x<970
9.(3分)如图,将一副直角三角板在平行四边形ABCD中作如下摆放,若∠1=30°,那么∠2=( )
A.60° B.75° C.70° D.35°
10.(3分)已知直线y1=kx+b(k>0)与x轴交于点(﹣2,0),直线y2=mx+b(n<0)与x轴交于点(3,0),据此推断不等式kx+b≥mx+b>0的解集为( )
A.﹣2<x<3 B.0<x≤3 C.﹣2≤x<0 D.0≤x<3
二、填空题(本大题共6小题,每小题3分,满分18分)
11.(3分)若分式的值为0,则x的值为 .
12.(3分)如图,在△ABC中,点D是边BC上的一点.若AB=AD=DC,∠BAD=52°,则∠C的度数为 °.
13.(3分)如图,在 OABC中,A(1,2),CO=4,将 OABC绕O点逆时针方向旋转90°到 OA'B'C'的位置,则点B'的坐标是 .
14.(3分)如图,在△ABC中,∠ACB=90°,DF垂直平分线段AC,E为CF的中点,连接DE,若DE=1.5,则AB的长为 .
15.(3分)如图,在四边形ABCD中,AD∥BC,BC>AD,E为AD的中点,将AB,CD分别平移到EF和EG的位置,若AE=3,BC=10,则FG的长为 .
16.(3分)如图,在平行四边形ABCD中,∠ABC,∠BCD的平分线BE,CF分别与AD相交于点E,F,BE与CF相交于点G,有下列结论:
①BE⊥CF;
②AF=DE;
③若连接BF,CE,则S△BFG=S△CEG;
④若,,则BE=4.
其中,正确的结论是 .(填写序号即可)
三、作图题(本大题满分4分)请用直尺、圆规作图,不写作法,但要保留作图痕迹.
17.(4分)已知:∠α,线段a.
求作:等腰△ABC,使得顶角∠A=∠α,底边BC上的中线长为线段a的长度.
四、解答题(本大题共8小题,满分68分)
18.(8分)计算:
(1)解不等式组:,并求出该不等式组的最大整数解;
(2)分解因式:a2﹣2a(b+c)+(b+c)2.
19.(6分)先化简,然后从﹣1,0,1,2四个数中选择一个合适的数代入求值.
20.(6分)某校学生会组织七年级和八年级共50名学生参加环保活动,七年级学生平均每人收集16个废弃塑料瓶、八年级学生平均每人收集24个废弃塑料瓶,请你根据以上信息,设计一个可以用一元一次不等式解决的问题,并给出解决方案.
21.(6分)命题“在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半”.
(1)请依据命题画出图形,并写出已知,求证;
(2)写出证明过程.
22.(8分)在△ABC中,CD是△ABC的中线,E为CD的中点,过点C作CF∥AB与BE的延长线相交于点F.
(1)如图①,连接FD,判断四边形BDFC的形状并证明你的结论;
(2)如图②,连接AF,若∠ABC=90°,∠DCB=30°,求∠AFB的度数.
23.(10分)为落实青岛市促进中小学生全面发展“十个一”项目行动计划,某学校准备购进一批足球和篮球使更多的学生参与这两个体育项目.据了解,某体育用品超市每个足球的价格比篮球的价格贵30元,用2400元购买篮球的数量是用1500元购买足球数量的2倍.
(1)求每个足球和篮球的价格;
(2)学校决定购买足球和篮球共54个,且购买足球的数量不少于篮球的数量的一半,求本次购买最少花费多少钱?
(3)在(2)最少花费方案下,体育用品超市为支持学校体育活动,对足球提供9折优惠,篮球提供7.5折优惠.学校决定将节约下的资金全部用于再次购买足球和篮球(此时按原价购买,可以只购买一种),求再次购买足球和篮球的方案.
24.(12分)如图,在平面直角坐标系中,已知点A(20,0),B(14,8),C(0,8),动点P从原点O出发,沿x轴正方向匀速运动,速度为2cm/s;同时,动点Q从点B出发,沿射线BC方向匀速运动,速度为1cm/s.设运动时间为t(s).
(1)求直线AB的函数关系式;
(2)当t=4时,直线PQ与直线AB交于点D,求点D的坐标;
(3)当t为何值时,以A,B,Q,P为顶点的四边形为平行四边形.
25.(12分)综合实践课上,同学们展开了以“轴对称”为主题的探究活动.
实践操作:
四边形ABCD是平行四边形,AC⊥AD,∠D=45°,在边BC上取一点P,如图①,连接AP,点B关于AP的对称点为点B',连接B′P、B′A.
问题解决:
(1)当B′A与AC重合时,连接BB',AP与BB'有何位置和数量关系,请说明理由;
(2)如图②,当∠BAP=30°时,连接B'C,AP与BB'位置关系为 ,数量关系为 ;
(3)若,∠B'AC=15°时,求线段BP的长.
同课章节目录
