六年级上册数学北师大版圆的认识(二)课件(共18张PPT)
文档属性
| 名称 | 六年级上册数学北师大版圆的认识(二)课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 739.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-15 17:11:27 | ||
图片预览




文档简介
(共18张PPT)
第 一 单元 圆
第 3 课时 圆 的 认 识(二)
复习导入
圆是我们生活中常见的平面图形,对于圆,同学们都了解了哪些知识呢
除此之外,圆还有哪些奥秘呢?
今天,我们一起来探究圆的奥秘。
圆是由曲线围成的平面封闭图形。
圆心一般用字母O表示。它到圆上任意一点的距离都相等.
连接圆心到圆上任意一点的线段叫做半径。
圆心确定圆的位置,半径确定圆的大小。
……
探索新知
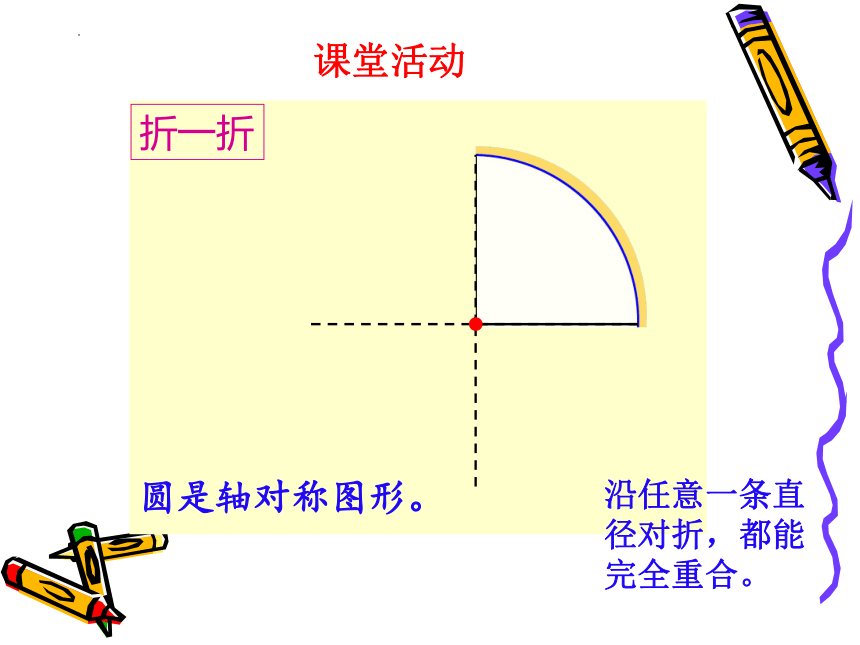
圆是轴对称图形吗?有几条对称轴?用一个圆形纸片,折一折。
请同学们拿出圆形纸片,动手试一试!
折一折
圆是轴对称图形。
课堂活动
沿任意一条直径对折,都能完全重合。
将圆沿直径对折,正好完全重合。圆是轴对称图形。
我发现圆有很多条对称轴,每条直径都是它的一条对称轴。
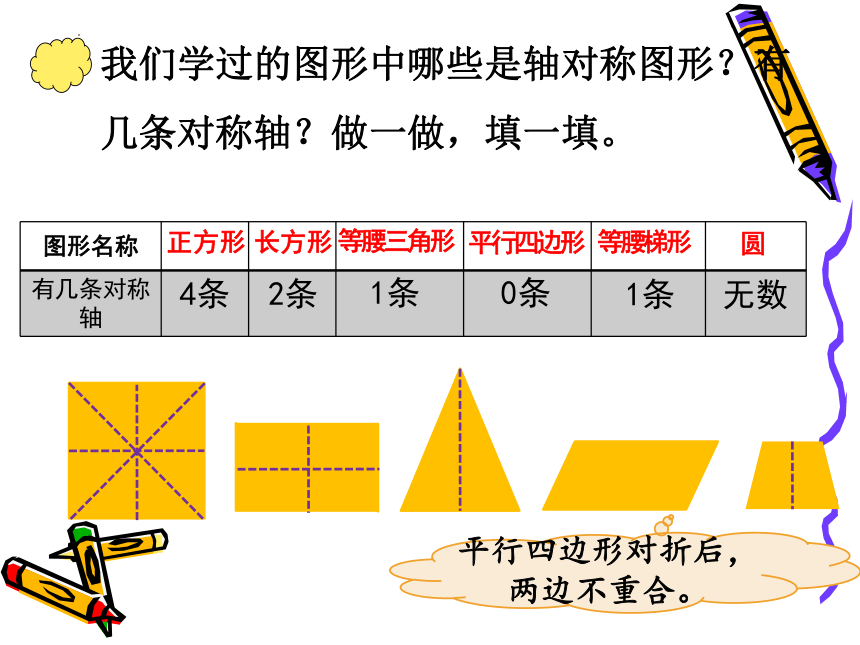
我们学过的图形中哪些是轴对称图形?有几条对称轴?做一做,填一填。
图形名称
有几条对称轴
正方形
长方形
4条
2条
等腰三角形
平行四边形
等腰梯形
圆
1条
0条
1条
无数
平行四边形对折后,两边不重合。
O
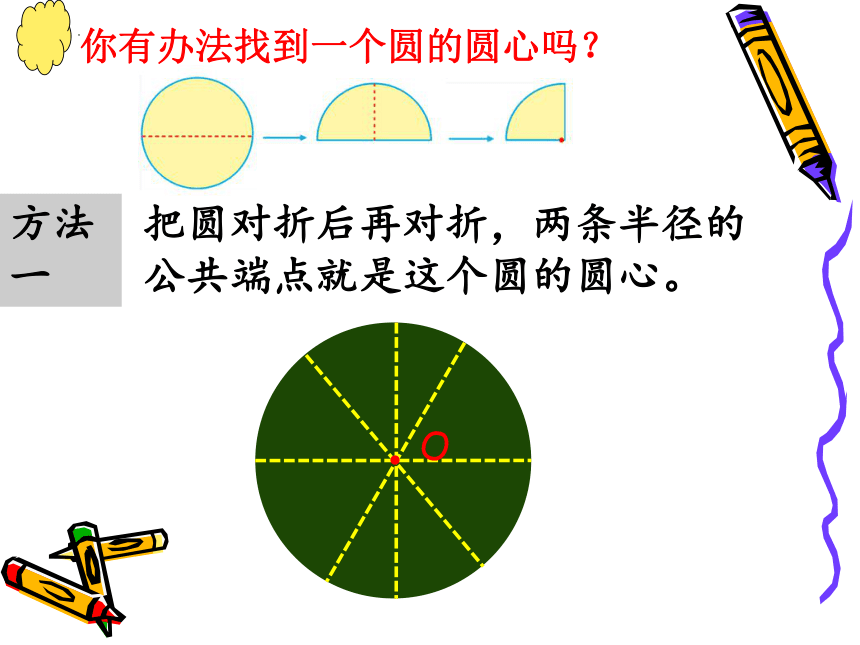
你有办法找到一个圆的圆心吗?
方法 一
把圆对折后再对折,两条半径的
公共端点就是这个圆的圆心。
情境导入
把圆沿直径所在的直线任意对折两次,折痕的交点就是圆心。
方法二
(1)把圆对折后再对折,两条半径的公共端点就是圆心;
(2)把圆沿直径所在的直线任意对折两次,折痕的交点就是圆心。
小结找圆心的方法
请找出下面各图的对称轴,与同伴进行交流。
4条
4条
6条
6条
由圆和正多边形组成的图形,对称轴
的条数由正多边形的对称轴的条数决定。
当圆形的圆心和正多边形的中心重合时,
正多边形的所有对称轴都是组合图形的对称轴。
画出这两个图形的对称轴。
1条
1条
正方形或正六边形的其中一条对称轴是组合图形的对称轴。
1.下面的图形是轴对称图形吗?画出轴对称图形的2条对称轴。
画法不唯一
画法不唯一
画法不唯一
2.小组合作,量一量,填一填。
(1)1元硬币的直径是 mm。
25
7.5-5=2.5(cm)
2.5cm=25mm
(2)照样子量一量1角和5角硬币的直径。
情境导入
3. 图中圆的位置发生了什么变化?
(1)从位置A向 平移 个方格到位置B,再向 平移 个方格到位置C。
右
4
右
6
(2)从位置C向 平移 个方格到位置D,再向 平移 个方格到位置E。
下
3
左
2
(3)从位置A到位置F,可以怎样平移。
方法一:从位置A向右平移8格,再向下平移2格到位置F。
方法二:从位置A向下平移2格,再向右平移8格到位置F。
4.剪下附页图1的圆、正方形和等边三角形,标出中心点A,并将各个图形分别与下面相对应的图形重合,然后沿中心点A转动图形,你发现了什么?
发现:
(1)正方形旋转90°后与原图形重合;等边三角形旋转120°后与原图形重合;圆无论旋转多少度都与原图形重合,所以圆有很好的旋转对称性。
(2)正方形旋转一周,与原图形重合4次;等边三角形旋转一周,与原图形重合3次;圆旋转一周,与原图形重合无数次。
课堂小结
1.圆是轴对称图形,有无数条对称轴。
2.通过对折可以找到圆的圆心。
第 一 单元 圆
第 3 课时 圆 的 认 识(二)
复习导入
圆是我们生活中常见的平面图形,对于圆,同学们都了解了哪些知识呢
除此之外,圆还有哪些奥秘呢?
今天,我们一起来探究圆的奥秘。
圆是由曲线围成的平面封闭图形。
圆心一般用字母O表示。它到圆上任意一点的距离都相等.
连接圆心到圆上任意一点的线段叫做半径。
圆心确定圆的位置,半径确定圆的大小。
……
探索新知
圆是轴对称图形吗?有几条对称轴?用一个圆形纸片,折一折。
请同学们拿出圆形纸片,动手试一试!
折一折
圆是轴对称图形。
课堂活动
沿任意一条直径对折,都能完全重合。
将圆沿直径对折,正好完全重合。圆是轴对称图形。
我发现圆有很多条对称轴,每条直径都是它的一条对称轴。
我们学过的图形中哪些是轴对称图形?有几条对称轴?做一做,填一填。
图形名称
有几条对称轴
正方形
长方形
4条
2条
等腰三角形
平行四边形
等腰梯形
圆
1条
0条
1条
无数
平行四边形对折后,两边不重合。
O
你有办法找到一个圆的圆心吗?
方法 一
把圆对折后再对折,两条半径的
公共端点就是这个圆的圆心。
情境导入
把圆沿直径所在的直线任意对折两次,折痕的交点就是圆心。
方法二
(1)把圆对折后再对折,两条半径的公共端点就是圆心;
(2)把圆沿直径所在的直线任意对折两次,折痕的交点就是圆心。
小结找圆心的方法
请找出下面各图的对称轴,与同伴进行交流。
4条
4条
6条
6条
由圆和正多边形组成的图形,对称轴
的条数由正多边形的对称轴的条数决定。
当圆形的圆心和正多边形的中心重合时,
正多边形的所有对称轴都是组合图形的对称轴。
画出这两个图形的对称轴。
1条
1条
正方形或正六边形的其中一条对称轴是组合图形的对称轴。
1.下面的图形是轴对称图形吗?画出轴对称图形的2条对称轴。
画法不唯一
画法不唯一
画法不唯一
2.小组合作,量一量,填一填。
(1)1元硬币的直径是 mm。
25
7.5-5=2.5(cm)
2.5cm=25mm
(2)照样子量一量1角和5角硬币的直径。
情境导入
3. 图中圆的位置发生了什么变化?
(1)从位置A向 平移 个方格到位置B,再向 平移 个方格到位置C。
右
4
右
6
(2)从位置C向 平移 个方格到位置D,再向 平移 个方格到位置E。
下
3
左
2
(3)从位置A到位置F,可以怎样平移。
方法一:从位置A向右平移8格,再向下平移2格到位置F。
方法二:从位置A向下平移2格,再向右平移8格到位置F。
4.剪下附页图1的圆、正方形和等边三角形,标出中心点A,并将各个图形分别与下面相对应的图形重合,然后沿中心点A转动图形,你发现了什么?
发现:
(1)正方形旋转90°后与原图形重合;等边三角形旋转120°后与原图形重合;圆无论旋转多少度都与原图形重合,所以圆有很好的旋转对称性。
(2)正方形旋转一周,与原图形重合4次;等边三角形旋转一周,与原图形重合3次;圆旋转一周,与原图形重合无数次。
课堂小结
1.圆是轴对称图形,有无数条对称轴。
2.通过对折可以找到圆的圆心。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
