浙教版科学八上1.3浮力综合作业三之拔尖篇(难度大)(含答案)
文档属性
| 名称 | 浙教版科学八上1.3浮力综合作业三之拔尖篇(难度大)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2024-07-16 09:50:42 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浮力综合作业三之拔尖篇(难度大)
一.选择题(共20小题)
1.三个完全相同的长方体木块,把它们分别放在三种密度不同的液体里,木块静止时浸入液体的情况是:甲木块大部分浸入;乙木块一半浸入;丙木块小部分浸入,如图所示。若将三木块露出液面部分切除后,剩下部分分别放入原容器中,则木块露出液面部分的体积( )
A.甲最多 B.乙最多 C.丙最多 D.一样多
2.一实心小球分别放入装有足量的水、酒精的容器中时,所受的浮力分别为0.9牛、0.8牛,已知酒精的密度为0.8×103千克/米3.则小球的密度为( )
A.0.8×103千克/米3 B.0.9×103千克/米3
C.1.0×103千克/米3 D.缺少条件,无法计算
3.一个充气的气球下面挂一个金属块,把它们放入水中某处恰能悬浮,如图所示。如果轻轻触碰一下气球,则金属块和气球( )
A.仍能静止 B.向下运动 C.向上运动 D.都有可能
4.甲、乙两个完全相同的烧杯,装满水放在水平桌面上。将体积相同的两个小球A、B分别放在甲、乙烧杯中,小球静止时如图所示。甲、乙两杯水对容器底的压强分别为p甲和p乙,A、B两个小球受到的浮力分别是FA和FB,容器底部受到的压力为F1和F2,容器对桌面的压力分别为F甲和F乙,则下列判断中正确的是( )
A.p甲>p乙 B.FA>FB C.F1=F2 D.F甲<F乙
5.如图所示,在图甲中,用细线将一实心铁球浸没在水中静止,图乙中将一实心铜球浸没在煤油中静止。铁球所受重力为G铁;体积为V铁;铜球所受重力为G铜,体积为V铜。铁球和铜球所受细线的拉力大小相等,所受浮力分别为F铁和F铜,已知水的密度为ρ水,煤油的密度为ρ油,且ρ油<ρ水<ρ铁<ρ铜,则下列判断正确的是( )
A.V铜=V铁 B.V铜>V铁 C.F铜=F铁 D.F铜<F铁
6.如图,在水平桌面上,放有一个底面积为100cm2且高10cm的柱形容器,装有6cm深的水。现用细线吊着一个密度为0.6g/cm3,高10cm,横截面积为50cm2的实心物体A(不吸水);使物体A的下表面恰好与水面接触,容器的重力忽略不计,则下列说法正确的是( )
A.物体A的重力为0.3N
B.要使细线的拉力为0,A应竖直向下移动6cm
C.若用细针将A压入水中浸没,此时容器对桌面的压力为9N
D.若物体吸水,将A缓慢浸入水中,最终物体A漂浮且露出2cm,此时水对容器底的压强为900Pa
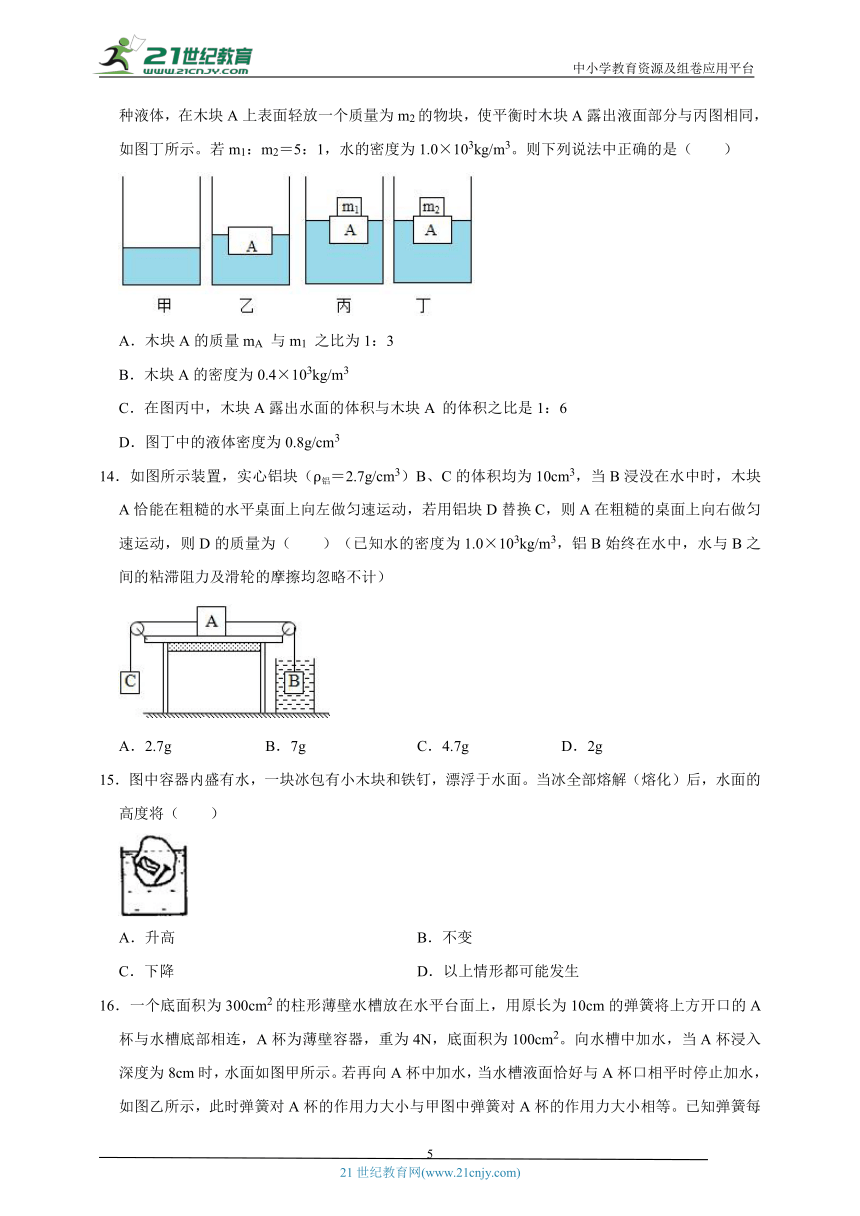
7.八中物理实验社团设计了顶部开有小孔的水库自动泄洪控制装置模型,如图所示。其中A为压力传感器,B是不吸水的圆柱体,能沿固定的光滑细杆在竖直方向自由移动。当模型内水深h1=15cm时,B与模型底面刚好接触且压力为零。水面上涨到设计的警戒水位时,圆柱体对压力传感器的压力为3N,触发报警装置,开启泄洪阀门。已知圆柱体B的底面积SB=100cm2,高hB=25cm,下列说法正确的是( )
①圆柱体B的密度0.6g/cm3
②刚触发报警装置时,B浸入水中的深度h2为12cm
③为了提高防洪安全性,使警戒水位比原设计低9cm,可在B的上方加上与B底面积相同、高为15cm、密度为0.4g/cm3的圆柱体C
④为了提高防洪安全性,增加圆柱体B高度为35cm,可使警戒水位比原设计低4cm
A.①③ B.②③ C.①④ D.①③④
8.有一重为2N的金属圆筒,口朝上放入水中时有的体积露出水面,如果在筒中倒入5×10﹣5m3的某种液体后,圆筒有体积露出水面,则筒内液体的密度是( )
A.1.2×103kg/m3 B.1.0×103kg/m3
C.2.0×103kg/m3 D.0.8×103kg/m3
9.如图所示,薄壁圆柱体容器的上半部分和下半部分的底面积分别为20cm2和30cm2,高度都为11cm,用轻杆连接一个不吸水的长方体放入容器中,长方体的底面积为15cm2、高为10cm,长方体的下表面距离容器底部始终保持6cm,现往容器内加水,当加入0.24kg和0.27kg水时,杆对长方体的作用力大小相等,(ρ水=1.0×103kg/m3,g取10N/kg)则长方体的密度为( )
A.0.6 g/cm3 B.0.7 g/cm3 C.0.9 g/cm3 D.1.1 g/cm3
10.如图所示,甲图中圆柱形容器中装有适量的水。将密度均匀的木块A放入水中静止时,有的体积露出水面,如图乙所示,此时水对容器底部的压强比图甲水对容器底部的压强增加了300Pa.若在木块A上表面轻放一个质量为m1的物块,平衡时木块A仍有部分体积露出水面,如图丙所示,此时水对容器底部的压强比图甲水对容器底部的压强增加了400Pa.若将容器中的水换成另一种液体,在木块A上表面轻放一个质量为m2的物块,使平衡时木块A露出液面部分与丙图相同,如图丁所示。若m1:m2=5:1,则下列说法中错误的是( )
A.木块A的质量mA与m1之比为1:3
B.在丁图中,液体的密度为0.8×103kg/m3
C.木块A的密度为0.6×103kg/m3
D.在图丙中,木块A露出水面的体积与木块A的体积之比是1:5
11.如图甲所示,一个柱形容器放在水平桌面上,容器中立放着一个底面积为100cm2,高为12cm,质量为900g的均匀实心长方体木块A,A的底部与容器底用一根细绳(细绳体积忽略不计)连在一起,已知细绳长度为L=8cm。现慢慢向容器中加水,当加入1.8kg的水时,木块A对容器底部的压力刚好为0,如图乙所示,若继续缓慢向容器中加水,直到细绳被拉断,然后停止加水,如图丙所示,细绳拉断前、后木块静止时,水对容器底部压强的变化量为50Pa,(整个过程中无水溢出),则下列说法正确的是( )
A.木块A的密度为7.5×103kg/m3
B.容器的底面积为200cm3
C.细绳拉断前物体所受到的浮力为10N
D.最后容器中水的总质量为4.5kg
12.如图所示,弹簧上端与物块m相连接,下端固定在容器底部。当物块浸没在水中静止时与浸没在酒精中静止时,弹簧的弹力大小相等。物块的体积为100cm3,酒精的密度为0.8×103kg/m3(不计弹簧质量及体积)其中正确的是( )
A.物块浸没在水中静止时弹簧对底部的拉力为0.2N
B.当弹簧脱离容器底部后静止时物块露出水面的体积为物块体积的
C.物块浸没在酒精中静止时弹簧对物块的支持力是0.1N
D.物块的质量为0.9kg
13.如图所示,甲图中圆柱形容器中装有适量的水,将密度均匀的木块A放入水中静止时,有的体积露出水面,如图乙所示,此时水对容器底部的压强比图甲水对容器底部的压强增加了300Pa。若在木块A上表面轻放一个质量为m1的物块,平衡时木块A仍有部分体积露出水面,如图丙所示,此时水对容器底部的压强比图甲水对容器底部的压强增加了400Pa。若将容器中的水换成另一种液体,在木块A上表面轻放一个质量为m2的物块,使平衡时木块A露出液面部分与丙图相同,如图丁所示。若m1:m2=5:1,水的密度为1.0×103kg/m3。则下列说法中正确的是( )
A.木块A的质量mA 与m1 之比为1:3
B.木块A的密度为0.4×103kg/m3
C.在图丙中,木块A露出水面的体积与木块A 的体积之比是1:6
D.图丁中的液体密度为0.8g/cm3
14.如图所示装置,实心铝块(ρ铝=2.7g/cm3)B、C的体积均为10cm3,当B浸没在水中时,木块A恰能在粗糙的水平桌面上向左做匀速运动,若用铝块D替换C,则A在粗糙的桌面上向右做匀速运动,则D的质量为( )(已知水的密度为1.0×103kg/m3,铝B始终在水中,水与B之间的粘滞阻力及滑轮的摩擦均忽略不计)
A.2.7g B.7g C.4.7g D.2g
15.图中容器内盛有水,一块冰包有小木块和铁钉,漂浮于水面。当冰全部熔解(熔化)后,水面的高度将( )
A.升高 B.不变
C.下降 D.以上情形都可能发生
16.一个底面积为300cm2的柱形薄壁水槽放在水平台面上,用原长为10cm的弹簧将上方开口的A杯与水槽底部相连,A杯为薄壁容器,重为4N,底面积为100cm2。向水槽中加水,当A杯浸入深度为8cm时,水面如图甲所示。若再向A杯中加水,当水槽液面恰好与A杯口相平时停止加水,如图乙所示,此时弹簧对A杯的作用力大小与甲图中弹簧对A杯的作用力大小相等。已知弹簧每受1N的拉力时弹簧伸长0.5cm,不计弹簧的重力、体积及其所受的浮力。下列说法正确的是( )
①甲图中弹簧对A杯施加了竖直向下的拉力为4N
②与甲图相比,乙图中A杯向下移动的距离为2cm,水面上升1cm
③与甲图相比,乙图中水槽对桌面的压力增加了6N
④乙图中,打开阀门B,待水静止后,水对槽底的压强为2200Pa
A.①② B.②③ C.①④ D.①③
17.如图所示,甲图中圆柱形容器中装有适量的水,将密度均匀的木块A放入水中静止时,有的体积露出水面,如图乙所示,此时水对容器底部的压强比图甲水对容器底部的压强增加了300Pa.若在木块A上表面轻放一个质量为m1的物块,平衡时木块A仍有部分体积露出水面,如图丙所示,此时水对容器底部的压强比图甲水对容器底部的压强增加了400Pa.若将容器中的水换成另一种液体,在木块A上表面轻放一个质量为m2的物块,使平衡时木块A露出液面部分与丙图相同,如图丁所示。若m1:m2=5:1,水的密度为1.0×103kg/m3.则下列说法中正确的是( )
A.木块A的质量mA与m1之比为1:3
B.木块A的密度为0.6×103kg/m3
C.在图丙中,木块A露出水面的体积与木块A的体积之比是1:6
D.图丁与图甲比较,液体对容器底部的压强增加了320Pa
18.小明设计了如图甲所示的装置测量液体密度,不吸水的实心圆柱体A的高度h0=40cm,上表面与容器中的水面刚好相平,下表面与圆柱形容器底的距离h1=20cm,压力传感器可以显示物体B对其支撑面压力F的大小。现以400cm3/min的速度将水匀速抽出,40min恰能将水全部抽尽,压力传感器示数F随时间t变化的图象如图乙所示。已知圆柱形容器底面积S=400cm2,轻质细线无弹性但承受的拉力有一定限度。(忽略摩擦)下列说法正确的是( )
A.物体B所受的重力是120N
B.物体A的密度为1.6×103kg/m3
C.当绳子拉断时,压力传感器的示数为60N
D.改变圆柱形容器中的液体,使物体A浸没在液体中,用压力传感器的示数显示液体密度的大小,则此密度测量仪的测量范围为0.5×103kg/m3~2.0×103kg/m3
19.在一足够高的容器底部固定一轻质弹簧,弹簧原长10cm,弹簧上方连有正方体木块A,木块的边长为10cm,容器的底面积为200cm2,如图,此时弹簧长度为6cm(已知弹簧的长度每改变1cm,所受力的变化量为1N),现向容器内注入某种液体,当木块A有的体积浸入液体中时,弹簧恰好处于自然伸长状态;在木块A正上方放置一合金块B,静止时液面刚好浸没B,已知合金块的体积为100cm3,高为4cm。下列说法中不正确的是( )
A.木块A的重力为4N
B.液体的密度为0.8×103kg/m3
C.放置合金块B后液体对容器底部的压强为1440Pa
D.合金块B的重力为14.8N
20.如图所示,一边长为10cm的实心正方体塑料块挂于弹簧测力计正下方,此时弹簧测力计读数为5N,此时塑料块下方刚好与水面接触,且距底面积为300cm2的容器底部5cm,现往容器中缓慢加水,已知弹簧的形变量与受到的拉力成正比,即弹簧受到1N的拉力时伸长1cm。以下说法正确的是( )
A.塑料块的密度为5g/cm3
B.当加入1000cm3水时,正方体物块所受浮力为5N
C.当加入3000cm3水时,水对容器底的压强为1500Pa
D.当加水至塑料块刚好漂浮时停止加水,然后将容器内的水以50cm3/s的速度向外排出,同时向上拉动弹簧测力计,使物体以1cm/s的速度向上移动,则经过约2.86s之后,弹簧测力计示数再次回到5N
二.填空题(共10小题)
21.甲、乙两个柱形容器中分别盛有密度为ρ1、ρ2的液体。A、B是两个实心正方体,密度为ρA、ρB,所受的重力为GA、GB,体积为VA、VB,将A和B以不同的方式先后放入甲、乙两容器的液体中,如图所示。在甲容器中,A有的体积露出液面。在乙容器中,A、B通过细绳相连,B受到容器底的支持力为F支(B与容器底不密合),受到细绳的拉力为F拉。不计细绳的质量和体积,ρ1:ρ2=2:1,VA:VB=4:1,F支:F拉=1:3,则ρA:ρB= 。
22.在抗震救灾中,某舟桥部队利用冲锋舟为灾区开辟了水上生命线。人们乘坐的冲锋舟满载时排开水的体积是1.5m3,冲锋舟自重为0.6×104N,假设每人的平均质量为60kg。则:
(1)冲锋舟满载时所受的浮力是 N;
(2)为保证安全,这条冲锋舟最多能承载 人;
(3)冲锋舟底部0.5m深处所受水的压强 Pa.(g=10N/kg)
23.如图甲所示,装有部分水的试管竖直漂浮在容器内的水面上,试管内水面与容器底部的距离为h,试管壁的厚度不计,粗细均匀。现将某物块放入试管,物块漂浮在试管内的水面上,试管仍漂浮在容器内的水面上,此时试管内水面与容器底部的距离为h',如图乙所示,则h′ h(选填“>”“<”或“=”)。取走该物块,将另一物块完全浸没在该试管水中,发现试管内水面与容器底部的距离恰好又变为h,如图丙所示,若试管横截面积与容器横截面积之比为1:n,则新放入物块密度为 g/cm3。若外容器装的是盐水,内试管装的是纯水,放入另一物块仍满足液面高度h不变,则该新物块的密度又是 g/cm3。( )
24.利用一根吸管制作一个简易密度计
(1)为了让饮料吸管能竖直的漂浮在液体中,应在吸管的 (上端/下端)塞入一些铜丝作为配重,并用石蜡将吸管的下端封闭起来。若将它放入液体中后不能竖直漂浮,请提出改进做法 。
(2)这根吸管竖直漂浮在不同液体中时,液体的密度越大,它露出液面部分的长度 (越长/越短/不变),受到的浮力大小 (变大/变小/不变)。
(3)通过正确计算,在吸管上标出对应的刻度线,便制成了一个简易的吸管密度计。下列四种刻度的标示合理的是
(4)为了使测量结果更准确,如何使简易密度计上两条刻度线(如0.9、1.0)之间的距离大一些?写出一种方法。 。
25.如图所示,一根细绳悬挂一个半径为r、质量为m的半球,半球的底面与容器底部紧密接触,此容器内液体的密度为ρ,高度为H米,大气压强为p0,已知球体的体积公式是V=,球面积公式是S球=4πr2,圆面积公式是S圆=πr2.则液体对半球的压力为 。若要把半球从水中拉起,则至少要用 的竖直向上的拉力。
26.小华同学为了探究物体浸在水中所受浮力的有关规律。他将甲物体分别按如图(a)、(b)、(c)所示浸在水中;接着他将乙物体浸没在水中如图(d)所示:又将丙物体浸没在水中如图(e)所示,请根据实验现象和相关结论归纳得出结论:
(1)分析图(a)、(b)、(c)的实验,可初步得出结论
(2)分析图(d)、(e)的实验,可初步得出结论
(3)小华发现由图(d)、(e)的实验还可以计算出乙物体和丙物体的密度,则乙物体的密度为 。
27.如图甲,足够高的圆柱形容器,高处有一个注水口以10cm3/s速度均匀向该容器内注水,在容器正上方的天花板上,有一轻质细杆(体积忽略不计)粘合着由两个横截面积不同的实心圆柱体组成的组合工件,A、B的密度相同,图乙中的坐标记录了从注水开始到注水结束的1min内,水面高度h的变化情况。已知t1=14s和t2=58s时,杆对圆柱体组合工件的作用力之比为2:3,则A、B的密度为 kg/m3。
28.资料显示:牛奶中掺水量越多,牛奶密度越小。小丽想通过测定密度来比较二种牛奶品质的优劣,她自制了一个可测液体密度的“浮标”﹣﹣在竹筷子下面缠绕一些铁丝,如图甲所示。
(1)纯牛奶是 (选填“纯净物”或“混合物”)。
(2)分别将“浮标”浸入A、B两牛奶中,待静止后,筷子上与液面相平的位置分别标记为A和B,如图乙所示。比较标线A和B的上下位置,可知A、B牛奶的密度为ρA ρB,由此可知A、B牛奶品质的优劣。
(3)在实际调量过程中,发现“浮标”杆上的二条标记线靠得很近,为了更易区分,请你提出一条改进“浮标”的建议 。
29.如图所示,我国首艘航母“辽宁号”的排水量为67500t,当航母满载静止在水面上时受到的浮力为 N;舰体底部在水面下10m深处受到海水的压强是 Pa(g取10N/kg,ρ水=1.0×103kg/m3)。
30.在一个底面积为200平方厘米、高度为20厘米的圆柱形薄壁玻璃容器底部,放入一个边长为10厘米的实心正方体物块,然后逐渐向容器中倒入某种液体。右图反映了物块对容器底部压力的大小F与容器中倒入液体的深度h(0~6厘米)之间的关系。
由此可知这种液体的密度大小为 千克/米3,当倒入液体的深度h为12厘米时,物块对容器的底部压力的大小F大小为 牛。
三.实验探究题(共10小题)
31.小巴同学探究“浮力的大小与物体排开水所受重力的关系”的实验装置及过程如图所示:
(1)如图A到E所示,会影响实验结论的是图 的实验装置(填字母代号);
(2)在完善实验装置后,有如下实验步骤,你认为不重复操作且排序合理的应是 ;(填字母代号)
①将铁块挂在弹簧测力计上,弹簧测力计的读数为F1
②将铁块浸没在液体中,弹簧测力计的读数为F2
③将装有排出液体的小桶挂在弹簧测力计下,弹簧测力计读数为F3
④将空桶挂在弹簧测力计下,弹簧测力计读数为F4
A.①②③④
B.①④②③
C.④①②③
D.④②①③
(3)通过探究,若等式 成立(选用F1、F2、F3和F4表示),则得出阿基米德原理;
(4)为了得到更普遍得结论,下列继续进行的操作中不合理的是 ;(填字母代号)
A.用原来的方案和器材多次测量取平均值
B.用原来的方案将水换成酒精进行实验
C.用原来的方案将石块换成体积与其不同的铁块进行实验
(5)小蜀同学在图C的操作中,只将石块的一部分浸在水中,其他步骤操作正确,则 (选填“能”或“不能”)得到与(3)相同的结论;
(6)小鲁同学利用上述实验中的器材和木块,探究“漂浮在液面上的物体所受浮力的大小是否遵循阿基米德原理”,实验过程中不需要弹簧测力计的是图中 (填“A”“B”“C”“D”或“E”)所示步骤;
(7)小巴同学还想利用浮力测量木块的密度,他找来的实验器材有:木块、弹簧测力计(0~5N)、底部固定有滑轮的水槽、细线及足量的水:
①如图甲,先用弹簧测力计测木块的重力;再用细线绕过滑轮将木块与测力计连接起来接着往水槽中倒入适量的水,使木块浸没在水中,如图乙,木块在水中静止时测力计示数为1.6N。她利用定滑轮改变力的方向的作用,巧妙的得到了木块的密度为 kg/m3;
②实验完毕小巴收拾仪器时,发现弹簧测力计在竖直方向未使用时,指针始终指在0.1N处,则他测得的木块密度会比真实值 (选填“偏大”“偏小”或“不变”)。
32.小明按照教材中“综合实践活动”的要求制作简易密度计。
(1)取一根粗细均匀的饮料吸管,在其下端塞入适量金属丝并用石蜡封口。塞入金属丝的目的是 。
(2)将吸管放到水中的情景如图(a)所示,测得浸入的长度为H;放到另一液体中的情景如图(b)所示,测得浸入的长度为h。用ρ水、ρ液分别表示水和液体的密度,则ρ水 ρ液(选填“=”、“>”、“<”),用F水、F液分别表示吸管在水和液体中受到的浮力,则F水 F液(选填“=”、“>”、“<”),此外h与ρ水、ρ液及H的关系式为h= 。
(3)小明根据图(a)在吸管上标出1.0刻度线(单位g/cm3,下同),再利用上述关系式进行计算,标出了0.8、0.9、1.1、1.2的刻度线(图中未画出)。结果发现,1.1刻线在1.0刻线的 (选填“上”、“下”)方,相邻刻线的间距 (选填“均匀”、“不均匀”)。
(4)为检验刻度误差,小明取来食油,先用天平和量筒测量其密度,然后再用这个密度计测量。但操作时却出现了图(c)所示的情形,这让他很扫兴。难道实验就此终止了吗,根据经验或思考,在不更换食油的情况下,你认为可以进行怎样的尝试: 。
33.利用一根吸管制作一个简易密度计
(1)为了让饮料吸管能竖直的漂浮在液体中,应在吸管的下端塞入一些铜丝作为配重,并用石蜡将吸管的下端封闭起来。若将它放入液体中后不能竖直漂浮,请提出改进做法 。
(2)这根吸管竖直漂浮在不同液体中时,液体的密度越大,它露出液面部分的长度 (越长/越短/不变),受到的浮力大小 (变大/变小/不变)
(3)通过正确计算,在吸管上标出对应的刻度线,便制成了一个简易的吸管密度计。下列四种刻度的标示合理的是 。
(4)为了使测量结果更准确,如何使简易密度计上两条刻度线(如0.9、1.0)之间的距离大一些?写出一种方法。
34.在课外实践活动中,某物理实验小组利用一根饮料吸管制作了简易密度计,如图1所示。
(1)该简易密度计应用到的物理原理有 。(从力学角度分析,填写一种即可)
(2)应在吸管的 (选填“上端”或“下端”)塞入适当的物体作为配重,然后用石蜡将吸管的下端封闭起来,使饮料吸管能竖直的漂浮在液体中。
(3)吸管竖直漂浮在不同液体中时,液体的密度越大,它露出液面部分的长度 ,受到的浮力大小 (均选填“增大”、“减小”或“不变”)。
(4)通过正确计算,在吸管上标出对应的刻度线,便制成了一个简易的吸管密度计。图2四种刻度的标示合理的是 。
(5)为了使测量结果更准确,便要使简易密度计上两条刻度线(如0.9、1.0)之间的距离大一些,请写出一种改进方法 。
35.学习浮力知识后,小华想制作一个密度计,他制作步骤如下:
a、取一根饮料吸管,将一些铁丝从吸管的下端塞入作为配重,并用石蜡将吸管的下端封起来。
b、将其漂浮在水中,在吸管上标出水面的位置,测出该位置到吸管下端的距离,即吸管浸入水中的深度H=5cm.如图所示。
c、推导:设吸管横截面积为S,在水中漂浮,故浮力与重力二力平衡,所以G=ρ水gSH;若漂浮在其它液体中,则浸入的深度h会因液体密度的改变而改变,但浮力仍与重力平衡,即G=ρ液gSh。
d、根据以上推导的公式,可计算出液体密度与下表中的密度相等时,简易密度计浸入的深度h(取密度的单位为g/cm3)
e小华做了五次实验,获得的数据如下:
实验次数 1 2 3 4 5
液体密度ρ/(g cm﹣3) 0.8 0.9 1.0 1.1
浸入的深度h/(cm) 6.3 5.6 5 4.5 4
(1)小华制作密度计的原理是利用了物体漂浮在液面时,浮力 重力(选填“大于”、“小于”或“等于”).步骤a中,将一些铁丝从吸管的下端塞入作为配重是为了降低吸管的 ,从而让它能够竖直的漂浮在液面上。
(2)通过对步骤c的分析,请推导出漂浮在ρ液液体中时,浸入深度h= (用ρ水、ρ液、H表达).在第5次试验中,观察到该密度计浸入某种液体的深度是4cm,则该液体的密度是 千克/米3
(3)分析表中数据或制作的密度计发现:简易密度计浸入液体的深度越大,表明液体的密度 (填“越大”“越小”“不变”),密度计的刻度线分布 (“是”或“不是”)均匀的。
(4)制作完毕后,小华分别测量可乐、色拉油等液体的密度,发现色拉油的密度在1.1和1.2之间,且两刻度线的距离较小,请提出一个方法使两条刻度线之间的距离大一些,使测量结果更精确。方法 。
36.为了研究物体漂浮在水面上时的特点,某小组同学用甲、乙两种材料制成体积不同的若干块物块进行实验,甲材料的密度为ρ甲,乙材料的密度ρ乙,且ρ甲<ρ乙.如图所示,他们让物块漂浮在水面上,测量并记录了物块的总体积和露出水面的体积,并将实验数据记录在下表中。
材料 实验 物块体积 露出水面体积 材料 实验 物块体积 露出水面体积
序号 (10﹣6米3) (10﹣6米3) 序号 (10﹣6米3) (10﹣6米3)
甲 1 10 6 乙 6 8 1.6
2 20 12 7 10 2
3 30 18 8 30 6
4 40 24 9 35 7
5 50 30 10 45 9
①分析比较实验序号 数据,可得出的初步结论是:同种材料的物块漂浮在水面上时,物块露出水面的体积与物块的体积成正比。
②分析比较实验序号1与7、3与8的数据,可得出的初步结论是: 。
③他们分别分析了“露出水面的体积”和“物体体积”的比例关系,可以得出的进一步结论是:
(a) 。
(b) 。
37.小明在生活中发现木块总浮在水面上,铁块却沉入水底,由此他提出两个问题:
问题1:浸入水中的铁块是否受到浮力?问题2:浮力大小与哪些因素有关?为此他做了进一步的猜想,设计并完成了如图所示实验。
(1)(b)(c)图中弹簧测力计示数均小于(a)图中弹簧测力计示数,说明浸入水中的铁块 (选填“受到”或“不受到”)浮力;
(2)做 (选填字母)两次实验,是为了探究铁块浸没在水中时所受浮力大小与深度是否有关;
(3)做(d)(e)两次实验,是为了探究浮力大小与 的关系。
38.小明同学用如图所示的实验器材和步骤,做了“验证阿基米德原理”的实验,
(1)该实验目的是:研究浸没在液体中的物体所受浮力与它排开液体 之间的关系。
(2)实验步骤有所遗漏,遗漏的步骤为 ,若将遗漏的步骤标注为E,则正确的实验步骤依次为 (填写实验步骤对应的字母)。
(3)实验中所测浮力的大小为 N,它应与 是相等的。
39.如图所示,在“探究影响浮力大小的因素”的实验中,物体A重为4N。
(1)弹簧秤读数时,视线应与刻度盘 。
(2)物体A在水中受到的浮力为 N。
(3)物体B的体积与A相同。则B所受重力为 N。
(4)图丙中液体的密度为 kg/m3。
40.阅读以下材料,回答相关问题。
我国国产第一艘航母
2017年4月26日,我国第一艘国产航母正式出坞下水。一瓶香槟酒摔碎舰艏,两舷喷射绚丽彩带,周边船舶一起鸣响汽笛,按照国际惯例举行“掷瓶礼”之后,国产航母缓缓移出船坞,停靠码头。这历史性的一刻,被定格为永恒的民族记忆,彰显着中国国家整体力量的提升。阳光下国歌声雄壮嘹亮,舰舷上五星红旗迎风招展。如果说现代文明由海洋文明开启,那么航母则是现代海军的标配,是一个民族海洋力量的象征。正因此,建设国产航母,不仅是捍卫国家利益、维护海洋权益、开发海洋文明的重要举措,更是中华民族几代人念兹在兹的百年梦想,是强军梦、强国梦的重要组成部分,寄托着中国人的民族情感。下水现场,不少人慕名而来、驻足观看;网络上,网友点赞“展示了中国速度、中国力量、中国智慧”;电视节目中,有嘉宾谈到海军发展历程喜极而泣…这个土生土长的“国之重器”,激荡着亿万人民内心深处的民族自信和爱国情怀。我们可以自豪地说:“我们已经拥有了两艘航母!”
图1是我国的“辽宁号”航母训练时的场景,图2是我国国产的第一艘航母建成下水的场景,下面是这两艘航母的一些相关参数:
“辽宁号”舰长304.5米,吃水线长270米,舷宽75米,吃水线宽:38米,吃水10.5米。标准排水量55000吨,满载排水量68000吨,最大航速32节。国产第一艘航母(暂时没有相关确切数据,大致搜集而成):舰长325米,甲板宽76.8米,吃水11米,标准排水量65000吨,满载排水量86000吨。
(1)2017年4月26日,这个日子是每一个中国人值得骄傲和自豪的,原因是
(2)我国的海军力量逐步壮大,航母从无到有,从有到多,体现了我国
(3)请你估算出我国国产航母的标准排水量,并写出合理的估算方法。
四.计算题(共20小题)
41.用同种金属材料做成A、B两个空心球,金属材料密度为2.5g/cm3,A球质量mA=1.037kg,B球质量mB=0.61kg。外径分别为RA=7cm,RB=5cm。两球空腔之间用一根金属导管相连,由于导管较细,故若施加过大的拉力会发生断裂。向A球空腔中注入300mL水,并在A、B两侧接上导线,连入一个报警电路(图中未画出)后横置于待监测液体表面。密度监测仪要求液体密度不得低于1.22g/cm3。该电路若检测到电流明显降低则触发报警。(球体体积计算公式为V=πr3,其中r为球体半径。为方便计算,可取π=3,g=10N/kg,忽略导管的重力与浮力,两侧导线始终松弛)同学们进行了下列研究:
(1)分别求出A装置和B装置的平均密度;(结果保留小数点后2位);
(2)若要保证装置准确报警,则导管所能承受的力需要满足什么条件?
(3)若此时液体的密度恰好低于1.22g/cm3,则与报警前相比,报警后A球在液面以上的体积如何变化?变化了多少?(假设报警后空腔内的水不会泄漏,以立方厘米为单位,结果保留到整数位)
42.小宁为了研究浸在液体中的物体所受浮力的规律,他设计了如图所示的实验。他将弹簧测力计一端固定,另一端挂边长为10cm正方体合金块A,放入底面积为300cm2装有水的圆筒形容器中,开始他将合金块A恰好浸没在水中,容器侧面的底部有一由阀门B控制的出水口,实验时,打开阀门B缓慢放水,放到弹簧测力计的读数不再变化时,立即关闭阀门B,在此过程中金属块始终不与容器底部接触,读出弹簧测力计示数的最小值和最大值分别为22N和32N,已知弹簧测力计每一牛顿刻度间的距离为1cm.求:
(1)在原图上作出关闭阀门B后水面的大致位置
(2)合金块A的重力及受到的最大浮力及其密度;
(3)从容器中排出水的质量。
43.如图所示,水平桌面上的圆柱形容器A的底面积为50cm2,中间自由的放入一个质地均匀的长方体物块B,物块B质量mB=160g、密度ρB=0.8×103kg/m3、底面积SB=20cm2,求:
(1)物块B对容器底部的压强。
(2)若沿器壁向A缓慢注入h=5cm深的水后,B将受到多大的浮力?
(3)向A缓慢注入质量为多克的水后,B对容器底的压力减小为零?
44.如图甲所示,水平面上有一底面积为5.0×10﹣8m2的圆柱形薄壁容器,容器中装有质量为0.5kg的水。现将一个质量分布均匀、体积为5.0×10﹣5m3的物块(不吸水)放入容器中,物块漂浮在水面上,物块浸入水中的体积为4.0×10﹣5m3。(g取l0N/kg,水的密度ρ水=1.0×103kg/m3)
(1)求物块受到的浮力大小。
(2)求物块的密度。
(3)如图乙用力F缓慢向下压物块使其恰好完全浸没在水中(水未溢出),求F大小。
45.水平桌面上放有一底部有水阀的圆柱形容器,容器重3N,底面积为250cm2,高10cm,在容器内装入部分水,将一个边长为10cm、密度为0.6g/cm3的正方体木块用细线悬挂在水中,如图(甲)所示,木块静止时有4cm浸入水中,求:
(1)此时木块所受的浮力为多少N?
(2)细线能承受的最大拉力为5N,打开水阀放水,绳子断开时水深7cm,如图(乙),立刻关闭水阀,木块漂浮静止时,水对容器底的压强为多少Pa?
(3)在(2)操作木块漂浮静止后,再用压力F作用在木块顶部将木块下压,如图(丙),求:当木块对容器底部压强为200Pa时,容器对桌面的压强为多少Pa?
46.一块浮冰浮在海面上,露出海面体积5m3.一质量为800kg的北极熊想爬到浮冰上捕食海豹,问:
(1)北极熊能否趴在冰面上?(取ρ海水=1.0×103kg/m3ρ冰=0.9×103kg/m3)
(2)整块浮冰质量多大?
47.如图所示,A、B是两个完全相同的容器,底面积为100cm2,分别盛有适量的煤油和水,置于水平桌面上。现将一实心小球分别放入A、B两容器中,小球静止后排开煤油和水的体积分别为20cm3和18cm3,求:
(1)小球在煤油中受到的浮力;
(2)小球的密度。(ρ煤油=0.8×103kg/m3,小球放入容器中均无液体溢出)。
48.一块质量为1.2kg的木块浮在水面上,它的密度是0.6×103kg/m3,木块漂浮在水面上时,受到的浮力是多大?要把木块全部浸入水中,至少需要加多大竖直向下的压力?
49.如图所示,已知重为10N的长方体木块静止在水面上,浸入在水中的体积占木块总体积的(g取10N/kg)。
(1)求木块所受浮力;
(2)若木块下表面所处的深度为0.2m,求木块下表面受到水的压强;
(3)求木块下表面面积;
(4)若要将木块全部浸没水中,求至少需要施加多大压力。
50.某物体的质量为2kg,体积为 3×10﹣3 m3.将其浸没在水中,g=10N/kg:
(1)此时物体受到多大的浮力?
(2)松手后,该物体是上浮,还是下沉?(计算说明)
(3)物体静止时,受到多大的浮力?(说明必要的理由)
51.在标准大气压下,将一质量是20克长15厘米的平底试管倒扣放在水中,试管的底面积为300毫米2,试管受到的浮力是多大?上面再放一质量是4克的物体,试管底刚好与水面相平,试管中水柱是多少厘米?试管内空气柱压强为多大?(不计空气的质量)
52.将边长是10cm的实心立方体木块轻轻地放入盛满水的大水槽内,待木块静止时,从水槽中溢出了600g水,取g=10N/kg,
求:(1)木块受到的浮力
(2)木块的重力
(3)若木块没入水中,它受的浮力。
53.如图甲所示,A、B为不同材料制成的体积相同的实心正方体,浸没在盛有水的薄壁圆柱形容器中,容器底面积是正方体下表面积的4倍,现在沿竖直方向缓慢匀速拉动绳子,开始时刻,A的上表面刚好与水面相平,A、B之间的绳子绷直,B在容器底部(未与容器底部紧密接触),A上端绳子的拉力是F,F随A上升的距离h变化的图像如图乙所示,除了连接A、B间的绳子承受拉力有一定限度外,其它绳子不会被拉断,绳的质量和体积忽略不计,求:
(1)正方体A的体积;
(2)正方体B的密度;
(3)整个过程中,水对容器底部压强的最小值。
54.如图甲所示,水平面上有一底面积为5.0×10﹣3m2的圆柱形薄壁容器,容器中装有质量为0.5kg的水,现将一个质量分布均匀、体积为5.0×10﹣5m3的物块(不吸水)放入容器中,物块漂浮在水面上,物块浸入水中的体积为4.0×10﹣5m3.(g取10N/kg,水的密度ρ水=1.0×103kg/m3)。
(1)求物块受到的浮力大小;
(2)求物块的密度;
(3)用力缓慢向下压物块使其恰好完全浸没在水中(水未溢出)如图乙,求该力F的大小。
55.如图是湖南师范大学学生发明的水上自行车,车下固定5个充满气的气囊,每个气囊的体积均为3.0×10﹣2m3,已知该水上自行车的总质量为25kg,不计车轮浸入水中的体积。(g取10N/kg)
(1)当自行车停放在水面上没人骑行时,气囊排开水的总体积为多少?
(2)当质量为75kg的人骑行时,固定在正中间的1个气囊破裂,该自行车是否还能安全骑行?请通过计算说明。
56.如图甲所示,一个柱形容器放在水平桌面上,容器中立放着一个底面积为100cm2,高为12cm均匀实心长方体木块A,A的底部与容器底用一根细绳连在一起,现慢慢向容器中加水,当加入1.8kg的水时,木块A对容器底部的压力刚好为0,如图乙所示,此时容器中的水的深度为9cm。已知细绳长度为L=8cm,ρ水=1.0×103kg/m3.求:
(1)当木块A对容器底部的压力刚好为0,A受到的浮力;
(2)木块A的密度;
(3)若继续缓慢向容器中加水,当容器中的水的总质量为4.5kg时,停止加水,如图丙所示,此时将与A相连的细绳剪断,求细绳剪断前、剪断后木块静止时,水对容器底部压强的变化量。(整个过程中无水溢出)
57.宋朝的怀丙和尚利用船的浮力打捞万斤的铁牛,如图甲,受此启发,小李同学设计了如图乙利用浮力打捞物品的装置。乙图所为一个足够高的柱形容器,待打捞物体A质量为1.5kg,底面积为100cm2,高10cm;浮体B质量为1kg,底面积为200cm2,高为10cm,A、B 正中央用一个不计质量和体积的弹簧相连。已知弹簧原长为10cm,弹簧每受到1N的拉力会伸长0.5cm。
(1)浮体B的密度是多少;
(2)当柱状容器里面加水,直到弹簧处于原长时,B物体排开水的体积是多少?
(3)继续加水直到A物体刚好离开容器底部时停止,这时水对容器底的压强比弹簧处于原长时增加多少?
58.悬浮在海水中的潜艇排开海水的质量为3×106kg(g=10N/kg,海水的密度取1×103kg/m3).求:
(1)潜艇排开的海水所受重力?
(2)潜艇所受浮力多大?
(3)潜水艇排开海水的体积?
(4)处于水下150m深度处有一个面积为2.4m2的舱盖,求它所受海水的压强和压力各是多大。
浮力综合作业三之竞赛篇(难度大,只适合优等生)
参考答案与试题解析
一.选择题(共20小题)
1.【分析】(1)物体漂浮时,露出液面部分的体积占总体积的比例是由物体的密度和液体的密度共同决定的,物体和液体的密度不变,露出液面部分的体积占总体积的比例也不变。
(2)因为甲木块大部分浸入;乙木块一半浸入;丙木块小部分浸入,所以可以假设甲木块有的体积浸入;乙木块有的体积一半浸入;丙木块有的体积浸入。
【解答】解:设长方体木块的体积为V,则将木块露出液面的部分切除后:
图中甲木块的体积为V浸入,木块再次露出液面部分的体积仍为现有体积的,即V甲=V×=V。
图中乙木块的体积为V浸入,木块再次露出液面部分的体积仍为现有体积的,即V乙=V×=V。
图中丙木块的体积为V浸入,木块再次露出液面部分的体积仍为现有体积的,即V丙=V×=V。
因为V>V,所以乙图木块再次露出液面部分的体积较大。
故选:B。
2.【分析】如果球在水中和酒精中都漂浮,则它受到的浮力都等于它的重力,即两球的浮力相同,这不符合题意,则不可能都漂浮;如果两球都浸没,设球的体积为V,则它受到的浮力之比为==,所以也不可能都浸没;故球只能在水中漂浮,在酒精中浸没。
【解答】解:小球在酒精中受到的浮力为:
F浮酒=ρ酒gV球=0.8N﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
因小球在水中漂浮,
所以小球受到的浮力和重力相等,
即:F浮水=ρ球gV球=0.9N﹣﹣﹣﹣﹣﹣﹣﹣②
联立①②两式可得:
ρ球=ρ酒=×0.8×103kg/m3=0.9×103kg/m3。
故选:B。
3.【分析】(1)气球在水中的深度不同、受压强不同、体积不同、排开水的体积不同、受到的浮力就要发生变化;
(2)气球和金属块的总重不变,根据物体的浮沉条件分析判断。
【解答】解:
原来气球和金属块悬浮在水中,F浮=G,
如果向上碰的话,由于气球受到水的压强变小、气球的体积变大,气球受到的浮力增大,大于自重,气球和金属块将向上运动;
如果向下碰的话,由于气球受到水的压强变大、气球的体积变小,气球受到的浮力减小,小于自重,气球和金属块将向下运动;
当水平碰,由于气球受到水的压强不变、气球的体积不变,气球受到的浮力不变,还等于自重,仍处于悬浮,还处于静止状态;
由以上分析和知静止、向上运动、向下运动都有可能。
故选:D。
4.【分析】A.由图可知,A、B两小球放在水中静止后,水面都与烧杯口相平,则烧杯中水的深度相等,由p=ρgh可知,水对烧杯底的压强相等;
B.根据小球静止后,A漂浮在水面,B沉在烧杯底,则VA排<VB排,由公式F浮=ρgV排可知,B球静止时受到的浮力大;
C.根据题意知,容器底部受到的压力等于剩余水的重力加上球的重力,甲杯A球漂浮,GA=F浮=G排,其对容器底的压力等于满杯水的重力;乙杯B球沉底,F浮=G排<GB,其对容器底的压力大于满杯水的重力;
D.根据阿基米德原理可知,判断出小球排开水受到的重力的大小关系,由容器对桌面的压力F=G容+G水﹣G排水+G球,比较出容器对桌面压力的大小关系。
【解答】解:A.由图可知,A、B两小球放在水中静止后,水面都与烧杯口相平,则烧杯中水的深度相等,由p=ρgh可知,水对烧杯底的压强相等,即p甲=p乙,故A错误;
B.根据小球静止后,A漂浮在水面,B沉在烧杯底,则VA排<VB排,由公式F浮=ρgV排可知,B球静止时受到的浮力大于A球静止时受到的浮力,即FA<FB,故B错误;
C.根据题意知,容器底部受到的压力等于剩余水的重力加上球的重力,甲杯A球漂浮,GA=FA浮=GA排,其对容器底的压力等于满杯水的重力;乙杯B球沉底,FB浮=GB排<GB,其对容器底的压力大于满杯水的重力,即F1<F2,故C错误;
D.根据浮沉条件和阿基米德原理得:FA=GA=GA排,FB=GB排<GB,由图可知,根据容器对桌面的压力F=G容+(G水﹣G排水)+G球可知,
F甲=G容+G水﹣GA排+GA=G容+G水,
F乙=G容+G水﹣GB排+GB>G容+G水,则F甲<F乙,故D正确。
故选:D。
5.【分析】对铁球和铜球进行受力分析,两者都受到竖直向下的重力、竖直向上的拉力和竖直向上的浮力作用,根据平衡力列出等式,再根据两者受到绳子的拉力相等列出等式,通过ρ油<ρ水<ρ铁<ρ铜,比较两者体积大小,再根据阿基米德原理判断浮力大小。
【解答】解:AB、如图甲,铁球受到竖直向下的重力G铁、竖直向上的拉力F拉和竖直向上的浮力F铁,
根据平衡力得,G铁=F铁+F拉,
如图乙,铜球受到竖直向下的重力G铜、竖直向上的拉力F'拉和竖直向上的浮力F铜,
根据平衡力得,G铜=F铜+F'拉,
因为,铁球和铜球所受细线的拉力大小相等,即F拉=F'拉,
所以,G铁﹣F铁=G铜﹣F铜,
由于铁球和铜球分别浸没在水和煤油中,
所以,ρ铁gV铁﹣ρ水gV铁=ρ铜gV铜﹣ρ油gV铜,
整理得,(ρ铁﹣ρ水)V铁=(ρ铜﹣ρ油)V铜,
由于ρ油<ρ水<ρ铁<ρ铜,
所以,ρ铁﹣ρ水<ρ铜﹣ρ油,
所以,V铁>V铜,故A和B都错误。
CD、根据阿基米德原理得,
铁球受到的浮力为:F铁=ρ水gV铁,
铜球受到的浮力为:F铜=ρ油gV铜,
因为ρ油<ρ水,V铜<V铁,
所以铜球受到的浮力小于铁球受到的浮力,即F铜<F铁,故C错误,D正确。
故选:D。
6.【分析】(1)利用重力计算公式G=mg=ρVg求得物体A的重力。
(2)要使细线的拉力为0,物体A受到的浮力等于重力,结合阿基米德原理求得排开液体的体积,进一步求得A竖直向下移动的距离和水上升的高度之和,据此求得A应竖直向下移动的距离;
(3)若用细针将A压入水中浸没,利用阿基米德原理求得A完全浸没所受的浮力,进一步求得细针对A的压力,即A对容器的压力,利用G=mg=ρVg求得水的重力,进一步求得容器对桌面的压力。
(4)若物体吸水,将A缓慢浸入水中,最终物体A漂浮,据此求得此时水对容器底的压力,利用压计算公式求得水对容器底的压强。
【解答】解:A、物体A的重力为:GA=mAg=ρAVAg=0.6×103kg/m3×10×10﹣2m×50×10﹣4m2×10N/kg=3N,故A错误;
B、要使细线的拉力为0,物体A受到的浮力等于重力,F浮=GA=3N,
结合阿基米德原理可知:==3×10﹣4m3,
A竖直向下移动的距离和水上升的高度之和为:h===0.06m=6cm,
则+=h,
,
解得V′=150cm3,
A竖直向下移动:==3cm,故B错误;
C、若用细针将A压入水中浸没,A完全浸没所受的浮力为:
F浮′=ρ水gV排′=1×103kg/m3×10×10﹣2m×50×10﹣4m2×10N/kg=5N,
细针对A的压力为:F压=F浮′﹣GA=5N﹣3N=2N,
此时溢出水的体积为V溢出=V物+V水﹣V容=50cm2×10cm+100cm2×6cm﹣100cm2×10cm=100cm3,
剩余水的体积:V剩余=V水﹣V溢出=100cm2×6cm﹣100cm3=500cm3,
容器中剩余水的重力为:
G水=m水g=ρ水V水g=1×103kg/m3×500×10﹣4m2×10N/kg=5N,
容器的重力忽略不计,容器对桌面的压力为:F=F压+G水+GA=2N+5N+3N=10N,故C错误;
D、若物体吸水,将A缓慢浸入水中,最终物体A漂浮,此时水对容器底的压力为:F′=GA+G水=3N+6N=9N,
水对容器底的压强为:p==900Pa,故D正确。
故选:D。
7.【分析】(1)根据当模型内水深h1=15cm时,根据体积公式求出B排开水的体积,根据B与模型底面刚好接触且压力为零可知B处于漂浮状态,根据阿基米德原理结合物体的漂浮条件求出B的重力,根据G=mg求出B的质量,根据密度公式求出B的密度;
(2)触发报警装置时,圆柱体B对压力传感器的压力为3N,由于力的作用是相互的,所以压力传感器对圆柱体B的压力也为3N,对B受力分析可得受到的浮力,根据F浮=ρ液gV排得B排开液体的体积,进一步求得B浸入水中的深度;
(3)根据刚触发报警装置时圆柱体对压力传感器的压力为3N结合力的平衡条件求出B受到的浮力,阿基米德原理求出B排开水的体积,根据体积公式求出B浸入水中的深度;根据刚触发报警装置时B浸入水中的深度和B的高度求出A到水面的距离,根据警戒水位需要比原设计低9cm求出此时A到水面的距离,进而表示出BC整体排开水的深度,根据体积公式和阿基米德原理表示出BC整体受到的浮力,根据体积公式、密度公式和G=mg表示出BC整体的重力,根据力的平衡条件表示出BC整体受到的浮力、圆柱体对压力传感器的压力和BC整体的重力之间的关系,解方程求出圆柱体C的高度;
(4)根据刚触发报警装置时B浸入水中的深度和B的高度求出B未增高前A到水面的距离,将圆柱体B的高度增加10cm,根据GB'=×GB可求出此时B的重力,由力的平衡条件可求出刚触发报警装置时B受到的浮力,根据阿基米德原理可求出此时B排开水的体积,从而求出此时B浸入水中的深度和A此时到水面的距离,从而求出警戒水位下降的高度。
【解答】解:①当模型内水深h=15cm时,水对容器底部的压强为
p=ρ水gh1=1.0×103kg/m3×10N/kg×0.15m=1500Pa,
此时B排开水的体积为
V排1=SBhl=100cm2×15cm=1500cm3=1.5×10﹣3m3,
由B与模型底面刚好接触且压力为零可知,此时B处于漂浮状态,由物体的漂浮条件可知,B的重力为
GB=F浮l=ρgV排1=1.0×103kg/m3×10N/kg×1500×10﹣6m3=15N,
B的密度为ρB====0.6×103kg/m3=0.6g/cm3,故①正确;
②触发报警装置时,圆柱体B对压力传感器的压力为3N,由于力的作用是相互的,所以压力传感器对圆柱体B的压力也为3N,对B受力分析可得,受到的浮力为
F浮2=G+F压=15N+3N=18N
根据F浮=ρ液gV排得,B排开液体的体积为V排2===1.8×10﹣3m3,
B浸入水中的深度为h2===0.18m=18cm,故②错误;
③由刚触发报警装置时B浸入水中的深度和B的高度可知,A到水面的距离
hA=hB﹣h2=25cm﹣18cm=7cm,
警戒水位需要比原设计低9cm时,A到水面的距离为
hA'=hA+9cm=7m+9cm=16cm,
则BC整体排开水的深度为
hBC=hC+hB﹣hA'=hC+25cm﹣16cm=hC+9cm,
BC整体排开水的体积为
VBC=SBhBC=100cm2×(hC+9cm)=(100hC+900)cm3,
此时BC整体受到的浮力为
F浮BC=ρ水gVBC=1.0×103kg/m3×10N/kg×(100hC+900)×10﹣6m3,
BC整体的体积为VBC=SB (hC+hB)=100cm2×(hC+25cm)=(100hC+2500)cm3,
由密度公式和G=mg可知,BC整体的重力为GBC=GB+GC=15N+0.4×103kg/m3×10N/kg×100×hC×10﹣6m3,
由力的平衡条件可知F浮BC=GBC+F,
代入得1.0×103kg/m3×10N/kg×(100hC+900)×10﹣6m3=15N+0.4×103kg/m3×10N/kg×100×hC×10﹣6m3+3N,
解得:hC=15cm,故③正确;
④B未增高前,A到水面的距离为hA=hB﹣h2=25cm﹣18cm=7cm,
增加圆柱体B高度为35cm,则此时B的重力为GB′===21N,
由力的平衡条件可知,刚触发报警装置时,B受到的浮力F浮3=GB′+F=21N+3N=24N,
由阿基米德原理可知,此时B排开水的体积V排3===2.4×10﹣3m3=2400cm3,
此时B浸入水中的深度h3===24cm,
此时A到水面的距离hA′=hB′﹣h3=35cm﹣24cm=11cm,
所以增加圆柱体B高度为35cm,则警戒水位比原设计低的距离为Δh′=hA′﹣hA=11cm﹣7cm=4cm,故④正确。
综上可知,D正确,ABC错误。
故选:D。
8.【分析】(1)金属筒容器有的体积露出水面,说明它漂浮,则浮力等于重力等于2N,利用阿基米德原理公式的变形公式:V排=计算出排开水的体积,然后除以就是金属筒的容积V物;
(2)利用阿基米德原理计算出金属筒有的体积没在水中时的浮力,则浮力减去金属筒的重力,就是5×10﹣4m3的某种液体的重力,然后利用公式ρ=计算液体密度。
【解答】解:(1)金属筒漂浮,F浮=G筒=2N。
∵F浮=ρ水V排g
∴V排===2×10﹣4m3,
∵的体积露出水面。
∴V筒==×2×10﹣4m3=3×10﹣4m3。
(2)装入液体后的浮力:F浮′=ρ水g(1﹣)V筒=1×103kg/m3×10N/Kg××3.0×10﹣4m3=2.4N,
装入液体后的浮力等于金属筒重力加上液体重力,所以:G液=F浮′﹣G筒=2.4N﹣2N=0.4N,
筒内液体的密度ρ====0.8×103kg/m3。
故选:D。
9.【分析】(1)首先分析加水0.24kg和0.27kg水位到达哪里。
(2)当加入0.24kg和0.27kg水时,杆对长方体的作用力大小相等,说明当加入0.24kg水时,物体受到竖直向下的重力、竖直向上的浮力和杆对物体的拉力,当加入0.27kg水时,物体受到竖直向下的重力和杆对物体向下的压力、竖直向上的浮力,物体的重力相等,根据重力相等列等式求解。
【解答】解:0.24kg=240g,0.27kg=270g
(1)如果把图中黄色部分加满,黄色部分是物体底部到容器底的部分,
h1=6cm,体积:V1=S1h1=30cm2×6cm=180cm3,加水质量:m1=ρV1=1.0g/cm3×180cm3=180g
(2)240g水剩余的质量:m2=240g﹣180g=60g,60g体积为:V2===60cm3,60g的水要加在绿色部分,
水面升高距离:h2===4cm
此时物体受到竖直向下的重力、竖直向上的浮力和杆对物体的拉力,G=F浮+F﹣﹣①
(3)继续加水,又加水270g﹣240g=30g,这30g水首先把红色部分填满,
红色部分高度:h3=11cm﹣6cm﹣4cm=1cm,红色部分的体积:V3=(S1﹣S)h3=(30cm2﹣15cm3)×1cm=15cm3,红色部分加水质量:m3=ρV3=1.0g/cm3×15cm3=15g
(4)把红色部分加满,剩余质量:m4=30g﹣15g=15g,15g水要加在蓝色部分,
蓝色部分的体积:V4===15cm3,蓝色部分的高度:h4===3cm
此时物体受到竖直向下的重力和杆对物体向下的压力、竖直向上的浮力,G=F'浮﹣F﹣﹣②
由①②得,F浮+F=F'浮﹣F,
ρ水gV排+F=ρ水gV'排﹣F,
ρ水gSh2+F=ρ水gS(h2+h3+h4)﹣F,
2F=ρ水gS(h2+h3+h4)﹣ρ水gSh2,
2F=ρ水gS(h3+h4),
2F=1.0×103kg/m3×10N/kg×15×10﹣4m2×(1+3)×10﹣2m,
解得,F=0.3N,
由①得,G=F浮+F
ρgV=ρ水gV排+F
ρ×10N/kg×15×10﹣4m2×10×10﹣2m=1.0×103kg/m3×10N/kg×15×10﹣4m2×4×10﹣2m+0.3N,
解得,ρ=0.6×103kg/m3=0.6 g/cm3
故选:A。
10.【分析】(1)设A的体积为V、容器的底面积为S,由于容器为圆柱形容器,在水中放入木块A后,A在水中漂浮,容器底受到的压力的变化值等于木块A的重力;而木块受到的浮力等于木块的重力,则压强变化值ΔP===;同理,比较甲丙图,压强变化值ΔP′==,知道ΔP、ΔP′的大小,可求丙图排开水的体积大小,进而求出木块A的质量mA与m1之比和木块A露出水面的部分占自身体积比值;
(2)在丙图中,由于m1和A漂浮,根据漂浮条件可得ρ水gV=GA+m1g,求出m1的大小;在丁图中,由于m2和A漂浮,根据漂浮条件可得ρ液gV=GA+m2g,求出m2的大小;由题知m1:m2=5:1,据此求出另一种液体的密度;
(3)根据乙图中,木块漂浮时,浮力等于重力即可求出木块的密度。
【解答】解:(1)设A的体积为V、容器的底面积为S,
∵A在水中漂浮,
∴F浮=ρ水V排g=ρ水Vg=GA,
甲图和乙图比较,容器底受到的压力差:ΔF=GA,
比较甲、乙两图,ΔP====300Pa,﹣﹣﹣﹣①
同理,比较甲丙图,ΔP′===400Pa,﹣﹣﹣﹣②
得:
mA:m1=3:1,
V排′=V;
此时木块A露出水面的部分占自身体积;故A错误,D正确。
(2)在丙图中,由于m1和A漂浮,可得:
ρ水gV=GA+m1g=ρ水gV+m1g,
∴m1=ρ水V,
在丁图中,ρ液gV=GA+m2g=ρ水gV+m2g,
∴m2=ρ液V﹣ρ水V,
∵m1:m2=5:1,
即:
(ρ水V):(ρ液V﹣ρ水V)=5:1,
解得:
ρ液=0.8ρ水=0.8×1.0×103kg/m3=0.8×103kg/m3.故B正确;
(2)在乙图中,木块漂浮,则
ρ水gV=ρ木gV
ρ木=ρ水=×1×103kg/m3=0.6×103kg/m3.故C正确。
故选:A。
11.【分析】(1)知道均匀实心长方体木块A的边长和体积,根据V=Sh求出其体积,利用ρ=求出木块A的密度;
(2)当加入1.8kg的水时,木块A对容器底部的压力刚好为0,此时木块恰好漂浮,根据物体浮沉条件和阿基米德原理求出木块排开水的体积,根据V=Sh求出容器内水的深度,根据ρ=求出容器内加入水的体积,利用V水=(S容﹣SA)h水求出容器的底面积;
(3)细绳拉断前、后木块静止时,根据p=ρgh求出容器内水深度的变化量,根据ΔV排=S容Δh求出木块排开水体积的减少量,然后求出剪断细绳前木块排开水的体积,根据阿基米德原理求出木块受到的浮力,根据V=Sh求出细绳拉断前木块浸入水中的深度,进一步求出容器内水的深度和容器内水的体积,根据m=ρV求出最后容器中水的总质量。
【解答】解:
(1)木块的体积:
VA=SAhA=100cm2×12cm=1200cm3,
木块的密度:
ρA===0.75g/cm3=0.75×103kg/m3,故A错误;
(2)当加入1.8kg的水时,木块A对容器底部的压力刚好为0,此时木块恰好漂浮,
因木块受到的浮力和自身的重力相等,
所以,由阿基米德原理可得F浮=G木=ρ水gV排,即m木g=ρ水gV排,
则木块排开水的体积:
V排===900cm3,
容器内水的深度:
h水===9cm,
容器内加入水的体积:
V水===1800cm3,
由V水=(S容﹣SA)h水可得,容器的底面积:
S容=+SA=+100cm2=300cm2,故B错误;
(3)细绳拉断前、后木块静止时,由p=ρgh可得,容器内水深度的变化量:
Δh===5×10﹣3m=0.5cm,
木块排开水体积的减少量:
ΔV排=S容Δh=300cm2×0.5cm=150cm3,
则剪断细绳前木块排开水的体积:
V排′=V排+ΔV排=900cm3+150cm3=1050cm3,
木块受到的浮力:
F浮′=ρ水gV排′=1.0×103kg/m3×10N/kg×1050×10﹣6m3=10.5N,故C错误;
细绳拉断前木块浸入水中的深度:
h水′===10.5cm,
容器内水的深度:
h水″=h水′+h绳=10.5cm+8cm=18.5cm,
容器内水的体积:
V水总=S容h水″﹣V排′=300cm2×18.5cm﹣1050cm3=4500cm3,
则最后容器中水的总质量:
m水总=ρ水V水总=1.0g/cm3×4500cm3=4500g=4.5kg,故D正确。
故选:D。
12.【分析】根据F浮=ρ水gV物 求得物块浸没在水和酒精中受到的浮力;然后对物块浸没在水中和酒精中进行受力分析,然后根据二力平衡列出等式首先求出物块的重力;
(1)根据力的平衡和力的相互作用即可求出弹簧对物块的支持力和弹簧对底部的拉力;
(2)当弹簧脱离容器底部后静止时物块处于漂浮状态,根据漂浮条件即可求出浸没的体积与物块的体积之比,然后求出露出水面的体积与物块体积的关系;
(3)根据G=mg即可求出物块的质量。
【解答】解:物块的体积V物=100cm3=1×10﹣4m3,物块浸没在水和酒精中时V排=V物=1×10﹣4m3,
物块浸没在水中:F浮=ρ水gV物=1.0×103kg/m3×10N/kg×1×10﹣4m3=1N。
物块浸没在酒精中:F浮′=ρ酒精gV物=0.8×103kg/m3×10N/kg×1×10﹣4m3=0.8N。
物块浸没在水中和酒精中受力分析分别如图甲、乙所示;
若物块都受弹簧的支持力,由于重力不变,浮力不同,故这种情况不可能;同理都受弹簧的拉力也不可能。
只可能是一个为拉力,另一个为支持力。由于物块在水中浮力大,物块会上浮,故弹簧会对它有拉力;在酒精中物块会受支持力作用。
所以根据物体受力平衡可得:
图甲中:F浮=F拉+G,
所以,F拉=F浮﹣G=1N﹣G﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
图乙中:F浮′+F支=G,
所以,F支=G﹣F浮′=G﹣0.8N﹣﹣﹣﹣﹣﹣﹣﹣﹣②,
已知:当物块浸没在水中静止时与浸没在酒精中静止时,弹簧的弹力大小相等;
即:F拉=F支,
所以,1N﹣G=G﹣0.8N
解得:G=0.9N;
A、物块浸没在水中静止时,弹簧会对物块的拉力为F拉=F浮﹣G=1N﹣0.9N=0.1N,
由于力的作用是相互的,则弹簧对底部的拉力F拉′=F拉=0.1N,故A错误;
B、当弹簧脱离容器底部后静止时物块处于漂浮,则:F浮″=G=0.9N,
根据F浮=ρ液gV排可得:V排″===9×10﹣5m3,
所以,===;故B错误;
C、物块浸没在酒精中静止时弹簧对物块的支持力F支=G﹣F浮′=0.9N﹣0.8N=0.1N;故C正确;
D、质量m===0.09kg,故D错误。
故选:C。
13.【分析】(1)设A的体积为V、容器的底面积为S,由于容器为圆柱形容器,在水中放入木块A后,A在水中漂浮,容器底受到的压力的变化值等于木块A的重力;而木块受到的浮力等于木块的重力,则压强变化值ΔP====;同理,比较甲丙图,压强变化值ΔP′==,知道ΔP、ΔP′的大小,可求丙图排开水的体积大小,进而求出木块A的质量mA与m1之比和木块A露出水面的部分占自身体积比值;
(2)在丙图中,由于m1和A漂浮,根据漂浮条件可得ρ水g V=GA+m1g,求出m1的大小;在丁图中,由于m2和A漂浮,根据漂浮条件可得ρ液g V=GA+m2g,求出m2的大小;由题知m1:m2=5:1,据此求出另一种液体的密度;
(3)根据乙图中,木块漂浮时,浮力等于重力即可求出木块的密度。
【解答】解:(1)设A的体积为V、容器的底面积为S,
∵A在水中漂浮,
∴F浮=ρ水V排g=ρ水(1﹣)Vg=GA,
甲图和乙图比较,容器底受到的压力差:ΔF=GA=mAg,
比较甲、乙两图,Δp====300Pa﹣﹣﹣﹣①
同理,比较甲丙图,Δp′====400Pa﹣﹣﹣﹣②
由 得:mA:m1=3:1,V排′=V;
此时木块A露出水面的部分占自身体积 ;故AC错误。
(2)在丙图中,由于m1和A漂浮,可得:
ρ水g V=GA+m1g=ρ水g V+m1g,
所以m1=ρ水V,
在丁图中,ρ液g V=GA+m2g=ρ水g V+m2g,
所以m2=ρ液V﹣ρ水V,
因为m1:m2=5:1,
即:(ρ水V):(ρ液V﹣ρ水V)=5:1,
解得:ρ液=0.8ρ水=0.8×1.0×103kg/m3=0.8×103kg/m3=0.8g/cm3.故D正确;
(3)在乙图中,木块漂浮,则ρ水gV=ρ木gV,
所以ρ木=ρ水=×1×103kg/m3=0.6×103kg/m3.故B错误。
故选:D。
14.【分析】要解决此题,需要掌握二力平衡条件,知道处于平衡状态的物体受平衡力的作用,一对平衡力的大小相等。
B在水中,所以受到水对它的浮力作用,所以B对A的拉力为F=G﹣F浮。
需要对物体A进行受力分析,确定两种情况下所受摩擦力的方向。根据二力平衡的条件列出两种情况下的关系式便可解决。
【解答】解:当用铝块C时,物体A向左匀速运动,所以所受摩擦力方向水平向右。
物体B在水中,受水对它向上的浮力,所以B对A的拉力FB=GB﹣F浮。
根据二力平衡条件:GC=f+GB﹣F浮
B、C是体积相同的实心铝块,所以重力相等。因此f=F浮。
若换为D,物体A向右匀速运动,所以所受摩擦力方向水平向左。
根据二力平衡条件:GD+f=GB﹣F浮,则GD=GB﹣f﹣F浮 又因为f=F浮,
所以GD=GB﹣2F浮 即mDg=ρ铝VBg﹣2ρ水VBg
则mD=ρ铝VB﹣2ρ水VB=2.7g/cm3×10cm3﹣2×1g/cm3×10cm3=7g
故选:B。
15.【分析】冰熔化前,由于冰、木块、铁钉处于漂浮状态,根据漂浮条件和阿基米德原理求排开水的体积;
冰熔化后,冰变成水,因为水的质量、重力不变,可求水的体积;木块仍然漂浮,根据漂浮条件和阿基米德原理求排开水的体积;铁钉下沉,根据阿基米德原理求排开水的体积;
计算冰熔化前后排开水的体积关系,得出水面升降。
【解答】解:
冰熔化前,冰和木块处于漂浮状态,
F浮=G冰+G木+G铁,
即:ρ水gV排=G冰+G木+G铁,
∴V排=++,
冰熔化后,冰变成水,木块仍然漂浮,铁钉下沉,
冰熔化成水的体积为:
V水==,
木块排开的水的体积为:
V木排=,
铁钉排开水的体积:
V铁=,
此时排开水的体积:
V=V水+V木排+V铁=++,
∵铁钉下沉,
∴F浮铁钉<G铁,
∵V<V排,
∴水面下降。
故选:C。
16.【分析】(1)根据体积公式计算A杯浸入水中的体积,根据F浮=ρ水gV排计算A杯受到的浮力;
对A进行受力分析可知:A受到竖直向下的重力和弹簧对A的拉力,以及竖直向上的浮力,进一步计算弹簧对A的作用力;
(2)如图乙所示,向A杯中加水杯子对弹簧的拉力减小,随着水的增多,拉力逐渐变为压力,
当水槽液面恰好与A杯口相平时停止加水,弹簧对A杯的作用力大小与甲图中弹簧对A杯的作用力大小相等,据此可知A杯对弹簧的压力,
弹簧每受1N的拉力时,弹簧伸长0.5cm,据此计算计算两图中弹簧长度的变化,据此可知与甲图相比,乙图中A向下移动的距离,进一步计算乙图中弹簧的长度和甲图水槽内水面高度,
根据体积公式计算与甲图相比,乙图水面上升的高度;
(3)由②可知乙图中A杯浸入水中的深度,根据体积公式、F浮=ρ水gV排计算乙图中A杯受到的浮力;
A杯受弹簧的支持力为4N,A杯和杯里的水受力平衡,即G杯+G水=F浮乙+F乙,代入数据解方程可得水的重力,
与甲图相比乙图水槽对桌面压力的增加量等于加入杯中的水的重力,据此可知水槽对桌面的压力增加了多少;
根据重力公式、密度公式计算A杯里的水的体积,根据体积公式计算A杯里的水的高度,根据连通器原理可知乙图中打开阀门B,待水静止后,水槽里面的水面高度的变化,根据液体压强公式计算水对槽底的压强。
【解答】解:(1)A杯浸入水中的体积为:V排=SAhA=100cm2×8cm=800cm3=8×10﹣4m3,
则A杯受到的浮力为:F浮=ρ水gV排=1×103kg/m3×10N/kg×8×10﹣4m3=8N;
对A进行受力分析可知:A受到竖直向下的重力和弹簧对A的拉力,以及竖直向上的浮力,
由二力平衡关系可知弹簧对A的作用力为:F拉=F浮﹣GA=8N﹣4N=4N,方向竖直向下,故①正确;
(2)如图乙所示,向A杯中加水杯子对弹簧的拉力减小,随着水的增多,拉力逐渐变为压力,
当水槽液面恰好与A杯口相平时停止加水,弹簧对A杯的作用力大小与甲图中弹簧对A杯的作用力大小相等,所以此时弹簧对A杯的支持力大小为4N,即A杯对弹簧的压力为4N,
弹簧每受1N的拉力时,弹簧伸长0.5cm,此时弹簧被压缩了2cm,
甲图中弹簧对A杯竖直向下的拉力为4N,弹簧被拉长了2cm,与甲图相比,乙图中A向下移动的距离为4cm,
如图:
则乙图中弹簧的长度l′=l+2cm﹣4cm=10cm+2cm﹣4cm=8cm,
甲图水槽内水面高度h=l+2cm+h1=10cm+2cm+8cm=20cm,
A杯浸入水中的深度为8cm,向A杯加水时,水槽中的水体积不变,
与甲图相比,乙图水面上升Δh===2cm,故②错误;
(3)由②可知,乙图中A杯浸入水中的深度为h2=8cm+4cm+2cm=14cm,
乙图中A杯受到的压力为F浮乙=ρ水gV排乙=1×103kg/m3×10N/kg×(14×100)×10﹣6m3=14N;
A杯受弹簧的支持力为4N,A杯和杯里的水受力平衡,即G杯+G水=F浮乙+F乙,
代入数据可得4N+G水=14N+4N,解方程可得水的重力G水=14N,
与甲图相比乙图水槽对桌面压力的增加量等于加入杯中的水的重力,即水槽对桌面的压力增加了14N,故③错误;
杯里的水的体积:V水===0.0014m3=1400cm3,
杯里的水的高度hA===14cm,
则A杯内外水面相平,乙图中打开阀门B,此时水杯和水槽相当于连通器,待水静止后,水槽里面的水面高度不变,
水槽里面的水面高度:h′=h+Δh=20cm+2cm=22cm=0.22m,
水对槽底的压强为p=ρ水gh′=1.0×103kg/m3×10N/kg×0.22m=2200Pa,故④正确。
故选:C。
17.【分析】(1)设A的体积为V、容器的底面积为S,由于容器为圆柱形容器,在水中放入木块A后,A在水中漂浮,容器底受到的压力的变化值等于木块A的重力;而木块受到的浮力等于木块的重力,则压强变化值Δp===;同理,比较甲丙图,压强变化值Δp′==;比较甲丁图,压强变化值Δp″=;知道Δp、Δp′的大小,可求丙图排开水的体积大小,进而求出木块A的质量mA与m1之比、木块A露出水面的部分占自身体积比值和图丁与图甲比较,液体对容器底部的压强变化值;
(2)根据乙图中,木块漂浮时,浮力等于重力即可求出木块的密度。
【解答】解:设A的体积为V、容器的底面积为S,
A在水中漂浮,
所以F浮=ρ水V排g=ρ水Vg=GA,
甲图和乙图比较,容器底受到的压力差:ΔF=GA,
比较甲、乙两图,Δp====300Pa,﹣﹣﹣﹣①
同理,比较甲丙图,Δp′===400Pa,﹣﹣﹣﹣②
比较甲丁图,Δp″=﹣﹣﹣﹣③
得:
=,=,
解得mA:m1=3:1,
V排′=V;
此时木块A露出水面的部分占自身体积,即木块A露出水面的体积与木块A的体积之比是1:5,故A错误,C错误。
在乙图中,木块漂浮,则
ρ水gV=ρ木gV
ρ木=ρ水=×1×103kg/m3=0.6×103kg/m3.故B正确。
②﹣①得:=100Pa,则G1=100Pa×S﹣﹣﹣﹣﹣﹣﹣④,
已知m1:m2=5:1,则G2=G1=×100Pa×S=20Pa×S﹣﹣﹣﹣﹣⑤,
由①可得,GA=300Pa×S﹣﹣﹣﹣﹣﹣⑥,
丙丁两图中物体都漂浮,且由题意可知,A排开水的体积相同,则:
G1+GA=ρ水gV排﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑦
G2+GA=ρ液gV排﹣﹣﹣﹣﹣﹣﹣﹣﹣⑧
将④⑤⑥代入⑦⑧解得:ρ液=0.8ρ水,
因丙丁两图中水和液体的体积相同,则G液=0.8G水,
图丁中液体对容器底部的压强:
p丁===320Pa+,
图甲中水对容器底部的压强:
p甲=,
所以,图丁与图甲比较,液体对容器底部的压强增加量:
Δp″=p丁﹣p甲=320Pa+﹣=320Pa﹣,故D错误。
故选:B。
18.【分析】(1)由图乙可知,压力传感器的示数先减小,到15min时突然增大到200N不变,说明绳子无拉力,此时F=GB;
(2)由图甲可计算水和圆柱体的总体积V=S容器h总,由抽水速度和抽水时间可知V水,即可求得VA,再由阿基米德原理求A浸没时受到的浮力;根据A受力平衡可求A的重力,根据G=mg求出A的质量,利用ρ=求出A的密度;
(3)由VA及h0,可求SA;由图乙可知,t=15min时绳子拉断,根据抽水速度求出此时容器里的水面下降的高度,据此可知A浸入水的深度,即可求得A排开水的体积VA排,由阿基米德原理求A浸没时受到的浮力;根据A受力平衡可求绳子的拉力和压力传感器的示数;
(4)利用图象,结合A、B的受力确定A浸没时所受浮力的最大值和最小值,再由阿基米德原理求液体的密度。
【解答】解:A、由图乙可知,随水位下降,压力传感器示数应不断减小,在A脱离液面时达到稳定,而图乙中15min时示数突然增大,可推断此时绳子突然断开(达到了绳子的最大承受力),故15min后压力传感器的示数等于B所受的重力,即GB=F=200N,故A错误;
B、由图甲可知,水和圆柱体的总体积:
V=S容(h0+h1)=400cm2×(40cm+20cm)=400cm2×60cm=24000cm3,
由于以400cm3/min的速度将水抽出,40min恰能将水全部抽出,则水的体积为:
V水=400cm3/min×40min=16000cm3,
则圆柱体A的体积:
VA=V﹣V水=24000cm3﹣16000cm3=8000cm3=8×10﹣3m3,
因为物体A不吸水,浸没时排开水的体积等于自身体积,即
V排=VA=8×10﹣3m3,
依据阿基米德原理可得,A浸没时所受的浮力:
F浮1=ρ水gV排=1.0×103kg/m3×10N/kg×8×10﹣3m3=80N;
由图乙可知,分析B的受力,当压力传感器示数F1=120N时,绳子的拉力:
F拉1=GB﹣F1=200N﹣120N=80N,
分析A的受力,受重力GA、绳子的拉力F拉1和水的浮力F浮1,则有GA=F拉1+F浮1=80N+80N=160N,
物体A的质量:mA===16kg,
物体A的密度为ρA===2×103kg/m3,故B错误;
C、由VA=8000cm3,h0=40cm可得圆柱体的底面积
SA===200cm2;
由图乙可知,t=15min时绳子拉断,则此时抽出的水的体积为:
V水′=400cm3/min×15min=6000cm3,
则水面下降的高度为:Δh===30cm,
此时圆柱体A浸入水的深度:h浸=h0﹣Δh=40cm﹣30cm=10cm,
此时A物体排开液体的体积为V排′=SAh浸=200cm2×10cm=2000cm3=2×10﹣3m3,
A物体所受浮力:F浮2=ρ水gV排′=1.0×103kg/m3×10N/kg×2×10﹣3m3=20N;
根据受力平衡可知:F拉2=GA﹣F浮2=160N﹣20N=140N,
压力传感器的示数F2=GB﹣F拉2=200N﹣140N=60N,故C正确;
D、因绳子的最大拉力Fmax=F拉2=140N,
由于A的重力为GA=160N,则A所受浮力最小为:F浮小=GA﹣F拉max=160N﹣140N=20N,
且A浸没在液体中时V排=VA=8×10﹣3m3,
则液体的最小密度为ρ最小===0.25×103kg/m3;
A浸没时所受的最大浮力与A的重力相等,即F浮大=GA=160N,则可测量的液体密度最大为:
ρ最大===2×103kg/m3,
所以该密度测量仪的测量范围是0.25×103kg/m3~2×103kg/m3,故D错误。
故选:C。
19.【分析】(1)根据题意可知弹簧上方连有正方体木块A时弹簧的压缩量,利用“弹簧的长度每改变1cm,所受力的变化量为1N”求出弹簧产生的弹力,物体A静止时受到的重力与弹簧产生的弹力是一对平衡力,据此求出物体A的重力;
(2)根据V=L3求出木块的体积,当木块A有的体积浸入液体中时,弹簧恰好处于自然伸长状态,则木块处于漂浮状态受到的浮力和自身的重力相等,根据F浮=ρgV排求出液体的密度;
(3)先求出木块A有的体积浸入液体中时液体的深度,根据体积公式求出此时容器内液体的体积,在木块A正上方放置一合金块B,静止时液面刚好浸没B,利用V=Sh求出此时液体的深度,利用p=ρgh求出放置合金块B后液体对容器底部的压强;
(4)在木块A正上方放置一合金块B,静止时液面刚好浸没B时,先求出弹簧的长度,然后求出弹簧的压缩量,进一步求出此时弹簧产生的向上弹力,根据F浮=ρgV排求出A、B受到的总浮力,以A、B整体为研究对象,整体受到竖直向下A和B的重力、竖直向上整体浮力和向上的弹力处于平衡状态,利用A、B整体受到的合力为零求出B的重力。
【解答】解:(1)由题意可知,弹簧上方连有正方体木块A时,其长度只有L1=6cm,则弹簧的压缩量Δx=L0﹣L1=10cm﹣6cm=4cm,
因弹簧的长度每改变1cm,所受力的变化量为1N,所以,弹簧产生的弹力F=4cm×1N/cm=4N,
因物体A静止时,受到的重力与弹簧产生的弹力是一对平衡力,所以,物体A的重力GA=F=4N,故A正确;
(2)木块的体积:VA==(10cm)3=1000cm3=1×10﹣3m3,
当木块A有的体积浸入液体中时,弹簧恰好处于自然伸长状态,则木块处于漂浮状态,木块受到的浮力F浮=G=4N,
由F浮=ρgV排可得,液体的密度:ρ液===0.8×103kg/m3,故B正确;
(3)当木块A有的体积浸入液体中时,液体的深度:h=L0+h浸=10cm+×10cm=15cm,
此时容器内液体的体积:V液=S容h﹣VA=200cm2×15cm﹣×1000cm3=2500cm3,
在木块A正上方放置一合金块B,静止时液面刚好浸没B,
则此时液体的深度:h′===18cm=0.18m,
则放置合金块B后液体对容器底部的压强:p=ρ液gh′=0.8×103kg/m3×10N/kg×0.18m=1440Pa,故C正确;
(4)在木块A正上方放置一合金块B,静止时液面刚好浸没B时,弹簧的长度L2=h′﹣LA﹣hB=18cm﹣10cm﹣4cm=4cm,
则弹簧的压缩量Δx′=L0﹣L2=10cm﹣4cm=6cm,
此时弹簧产生的向上弹力:F′=6cm×1N/cm=6N,
A、B受到的总浮力:F浮总=ρ液g(VA+VB)=0.8×103kg/m3×10N/kg×(1×10﹣3m3+100×10﹣6m3)=8.8N,
以A、B整体为研究对象,整体受到竖直向下A和B的重力、竖直向上整体浮力和向上的弹力处于平衡状态,
由A、B整体受到的合力为零可得:F浮总+F弹=GA+GB,
则B的重力:GB=F浮总+F弹﹣GA=8.8N+6N﹣4N=10.8N,故D错误。
故选:D。
20.【分析】(1)已知塑料块的边长,求出塑料块的体积;塑料块下方刚好与水面接触时,测力计测量塑料块的重力,根据G=mg求出塑料块的质量,利用ρ=即可求出塑料块的密度;
(2)当加入1000cm3水时,塑料块会上浮,由于塑料块受到的浮力等于测力计的示数变化,根据塑料块升高的高度,得出弹簧伸长量的变化,然后即可求出浮力;根据阿基米德原理求出塑料块浸入水中的体积(排开水的体积),则即可求出物体浸没的深度,
则两种情况下的高度之和就是水面变化的高度,根据底面积求出加入水的体积,由于加入水的体积已知,据此即可求出塑料块会上浮的高度hm,继而求出浮力。
(3)同上求出当加入3000cm3水时,塑料块会上浮的高度h′m,然后根据水的体积变化求出水的深度,利用p=ρgh求容器底部所受压强;
(4)当加水至塑料块刚好漂浮时说明塑料块受到浮力F浮″=G,根据F浮=ρgV排得塑料块漂浮时浸入水中的体积,然后求出浸入的深度,
由于物体向上移动时,塑料块底面以上周围的水会补充到塑料块下面,当向外排水后,弹簧测力计示数再次回到5N,即塑料块下方刚好与水面再次接触,
此时塑料块移动后塑料块下面的水的体积与排出的水的体积等于塑料块周围水的体积;据此即可求出需要移动的时间。
【解答】解:A、塑料块的体积V=L3=(10cm)3=1000cm3;
当塑料块底面刚好接触水面时。弹簧测力计示数为5N,即G=5N;
则塑料块的质量m===0.5kg=500g,
塑料块的密度ρ===0.5g/cm3;故A错误;
B、设当加入1000cm3水时,塑料块上浮hm,则弹簧的伸长将减小hm,
由于弹簧受到1N的拉力时伸长1cm,则弹簧的拉力减小量为ΔF1=100hN,
此时塑料块受到浮力F浮=ΔF1=100hN。
由F浮=ρgV排得此时塑料块浸入水中的体积:
V排==;
S塑料=L2=(10cm)2=100cm2=100×10﹣4m2,
则塑料块浸入水的深度为h浸==,
所以,S容器h+(S容器﹣S塑料)h浸=V加水,
即:S容器h+(S容器﹣S塑料)=V加水,
所以,300×10﹣4m2×hm+(300×10﹣4m2﹣100×10﹣4m2)×=1000×10﹣6m3,
解得:h=0.02,
所以当加入1000cm3水时,塑料块上浮0.02m,塑料块受到浮力:
F浮′=ΔF1=100hN=100×0.02N=2N;故B错误;
C、当所加的水使物块漂浮时,此时物块受到的浮力F浮=G=5N,
则V排===5×10﹣4m3=500cm3,
此时物块浸入水中的深度h浸===5cm,
最初的拉力为5N,则加水使物块漂浮时,拉力减小了5N,由题意可知弹簧会缩短5cm,即物块会向上移动5cm,
所以此时水的深度H=h0+h向上+h浸=5cm+5cm+5cm=15cm,
此时水对容器底的压强p=ρ水gh水=1.0×103kg/m3×10N/kg×0.15m=1500Pa,
所加水的体积:V加=S容器H﹣V排﹣S容器h0=300cm2×15cm﹣500cm3﹣300cm2×5cm=2500cm3,故C错误;
D、当加水至塑料块刚好漂浮时,则测力计的示数为零,所以,塑料块受到浮力F浮″=G=5N,
由F浮=ρgV排得塑料块浸入水中的体积:
V排″===5×10﹣4m3=500cm3;
则塑料块浸入水的深度为:h浸″===5cm,
此时塑料块底面以上的水的体积V′=(S容器﹣S塑料)h浸″=(300cm2﹣100cm2)×5cm=1000cm3,
当物体向上移动时,塑料块底面以上周围的水会补充到塑料块下面,则塑料块移动后下面的水的体积与排出的水的体积等于塑料块周围水的体积;
物体向上移动的高度为h物=v物t=1cm/s×t,
则塑料块上移后下面的水的体积:V下=S容器h物=S容器v物t=300cm2×1cm/s×t,
排出的水的体积V排出=v排t=50cm3/s×t,
所以,V下+V排出=V′,
即:300cm2×1cm/s×t+50cm3/s×t=1000cm3,
解得:t≈2.86s,故D正确。
故选:D。
二.填空题(共10小题)
21.【分析】整体分析甲,由题知,物体漂浮,有 的体积露出水面,利用阿基米德原理求出受到的浮力;
整体分析乙,因为在乙容器中,A、B通过细绳相连,所以物体A、B的重力等于其在液体中受到的浮力加上B受到容器底的支持力为F支;
隔离法分析乙,A物体的重力加上细绳的拉力等于它在此液体中受到的浮力;B物体的重力等于细绳的拉力加上它在此液体中受到的浮力,再加上B受到容器底的支持力;根据以上分析,列出算式,将已知条件代入及可求得结论。
【解答】解:
由题知,物体漂浮,有 的体积露出水面,此时浮力等于二者重力,则F浮=GA+GB=ρ1gVA﹣﹣﹣﹣﹣①
在乙容器中,A、B通过细绳相连,物体A、B的重力等于其在液体中受到的浮力加上B受到容器底的支持力为F支,即GA+GB=ρ2g(VA+VB)+F支﹣﹣﹣﹣②
单独对乙容器中的A物体进行受力分析,A物体受到的浮力等于A物体的重力加上细绳的拉力,即GA+F拉=ρ2gVA﹣﹣﹣﹣﹣③
B物体的重力等于细绳的拉力加上它在此液体中受到的浮力,再加上B受到容器底的支持力,即GB=F拉+ρ2gVB+F支﹣﹣﹣﹣﹣④
联立①②可得:F支=ρ1g×VA﹣ρ2g(VA+VB)﹣﹣﹣﹣﹣﹣﹣⑤
已知F支:F拉=1:3,即F拉=3F支﹣﹣﹣﹣﹣﹣﹣⑥
由③⑤⑥可得:mA=4ρ2VA﹣ρ1VA+3ρ2VB
由④⑤⑥可得:mB=3ρ1VA﹣4ρ2VA﹣3ρ2VB
已知ρ1:ρ2=2:1,VA:VB=4:1,
则ρA==4ρ2﹣ρ1+3ρ2=4ρ2﹣ρ1+3ρ2×=ρ2;
ρB==3ρ1×﹣4ρ2×﹣3ρ2=5ρ2;
故ρA:ρB=ρ2:5ρ2=1:20。
故答案为:1:20。
22.【分析】(1)已知冲锋舟满载时排开水的体积,根据公式F浮=ρgV排可求冲锋舟满载时所受的浮力;
(2)冲锋舟满载漂浮时所受的浮力等于自身的重力与人的重力之和;冲锋舟最多承载人的重力与自重的和等于满载时的浮力,从而求出最多超载的人数;
(3)已知冲锋舟底部所处的深度,根据公式P=ρgh可求所受的压强。
【解答】解:(1)冲锋舟满载时所受的浮力是F浮=ρgV排=1000kg/m3×10N/kg×1.5m3=1.5×104N;
(2)一个人的重力G=mg=60kg×10N/kg=600N;
最多承载的人数为n===15人;
(3)冲锋舟底部0.5m深处所受水的压强P=ρgh=1000kg/m3×10N/kg×0.5m=5×103Pa;
故答案为:1.5×104;15;5×103。
23.【分析】(1)根据物块m物1在试管内漂浮F浮1=G物1,求出Δh0表示试管中液体上升的高度的表达式;根据试管中放入物块使得试管整体受到的浮力的增加量ΔF浮1=G物1,即ρ水gΔh1S1=ρ水gS2Δh2求出试管底部浸入容器中水的深度的增加量Δh1、放置物块试管下沉容器液面上升的高度Δh2的表达式,结合放入物块后试管内水面与容器底部的距离h′与原h的关系h′=h﹣(Δh1﹣Δh2)+Δh0,与h比较大小做出判断;
(2)已知S2=nS1,试管始终漂浮,受到的浮力的增加量等于物块的重力ΔF浮1=G物1,即ρ水gΔH1S1=ρ水g(S2﹣S1)ΔH2求出ΔH2与ΔH1的关系;由题意知将另一物块完全浸没在该试管水中,发现试管内水面与容器底部的距离恰好又变为h,可知ΔH1﹣ΔH2=ΔH0,求出ΔH0与ΔH1的关系;进一步又因为试管仍然漂浮,所以新排开的水重等于新加入的物体重G物2=ΔF浮2=ρ水gΔV2,则m物2g=ρ物2 V物2=ρ水gΔV2,结合V排2=V物2=S1ΔH0、ΔV2=S1ΔH1以及物块的密度以及求解新物块的密度;
(3)若外容器装的是盐水,内试管装的是纯水,同理(2)进行分析。
【解答】解:
(1)设Sl表示试管底面积,S2表示容器底面积,当物块漂浮在试管内的水面上时,因物块m物1在试管内漂浮F浮1=G物1,物块1排开试管中水的体积V排1=Δh0S1,则有:ρ水gV排1=ρ水gΔh0S1=m物1g;
其中Δh0=,Δh0表示试管中液体上升的高度;
因放入物块1使得试管排开的容器中水的体积的增加量为:
ΔV1=S1Δh1=S2Δh2,
其中Δh1表示试管底部浸入容器中水的深度的增加量,Δh2表示容器中液面上升的高度,
因放入物块1使得试管受到的浮力的增加量ΔF浮1=G物1,
即ρ水gΔV1=ρ水gΔh1S1=ρ水gS2Δh2=m物1g,
故可解得:
Δh1=;
Δh2=;
则此时试管内水面与容器底部的距离为:
h′=h﹣(Δh1﹣Δh2)+Δh0=h﹣[﹣]+=h+>h;
(2)当放置另一物块2完全浸没在该试管时,物块2排开试管中水的体积,V排2=V物2=S1ΔH0,其中ΔH0表示试管中液体上升的高度;
因放置物块2后试管下沉,试管排开容器中水的体积的增加量:
ΔV2=S2ΔH1=S1ΔH浸=S1(ΔH1+d)
其中ΔH1表示因放置物块试管下沉使得容器液面上升的高度,ΔH浸表示试管底部浸入容器中水的深度的增加量,d为试管向下移动的距离;
又S2=nS1,可得d=(n﹣1)ΔH1;
由试管内水面与容器底部的距离恰好又变为h可知:ΔH0=d=(n﹣1)ΔH1;
因为试管仍然漂浮,所以新排开的水重等于新加入的物体重,ΔF浮2=G物2,即ρ水gΔV2=m物2g=ρ物2gV物2,结合ΔV2=S2ΔH1以及V排2=V物2=S1ΔH0,则物块的密度:
ρ物2=ρ水=ρ水=ρ水=ρ水;
(3)若外容器装的是盐水,内试管装的是纯水,放入另一物块3仍满足液面高度h不变,则以上结论依然成立,同理可得:ρ物3=ρ盐水。
故答案为:>;ρ水;ρ盐水。
24.【分析】(1)因为密度计是一根两端封闭即空心的,所以能使密度计浮在液体表面,为了使它保持竖直的漂浮,就在管的底部封存少许铅粒;
(2)密度计的质量一定,在液体中受力平衡,受到的浮力总是等于重力,被测液体的密度越大,排开液体的体积越小,浸入液体部分也越小,据此分析回答;
(3)根据密度计的刻度由上至下数值逐渐增大分析;
(4)为了使测量结果更准确,使密度计上两条刻度线(如0.9、1.0)之间的距离大一些,因为ΔV=sh,所以可知减小S,即可使h变大,据此设计即可。
【解答】解:
(1)为了让饮料吸管能竖直的漂浮在液体中,吸管下端塞入一些铜丝作为配重,这样做目的是让密度计竖直漂浮在液体中;若将它放入液体中后不能竖直漂浮,则可以用小钢珠作为配重;
(2)密度计是漂浮在液体中,所受浮力等于本身的重力,保持不变,如果液体的密度越大,则密度计浸入液体中的体积越小,即越往上浮,则露出液面部分的长度越长;所以密度计的刻度是越往下值越大;
(3)因为密度计是漂浮在液体中,所受浮力等于本身的重力,则F浮水=F浮液=G,即ρ水gSH水=ρ液gSh液=G,
∵h液=H水,h液和ρ液是反比例函数;
∴刻度分布不均匀。且密度计的刻度由上至下数值逐渐增大;当密度的变化大时h液越变化越小,故C正确;
(4)因为ΔV=sh,所以使h变大,应减小S即可,具体做法是:用更细的吸管。
故答案为:(1)下端;可以用小钢珠作为配重(重心比铜丝低的材料都可以);
(2)越长;不变;
(3)C;
(4)用更细的吸管;
25.【分析】浸没在液体中的固体受到的浮力等于固体各表面所受液体压力的合力;我们可以先设想半球体下表面有液体,求出此时下表面受到的液体压力和半球体受到的浮力,从而求出此时液体对半球体上表面的压力;然后对半球体进行受力分析,求出把半球体从水中拉起需要的拉力。
【解答】解:(1)假设半球下表面处全部为液体,
则半球受到的浮力F浮方向竖直向上,由阿基米德原理可知,
F浮=ρgV排=ρgV半球=ρg××πr3=ρgπr3;
半球表面各处所受液体压力的分布如图所示,
半球上表面受到的液体压力F上竖直向下,
由p=可得,半球下表面受到的液体压力:
F下=p下S圆=p液S圆=ρgH×πr2,方向竖直向上,
半球受到的浮力F浮等于半球下表面与上表面所受液体对它的压力的合力,
即:F浮=F下﹣F上,F上=F下﹣F浮=ρgH×πr2﹣ρgπr3,
在本题给出的条件中,半球底部与容器底部紧密接触,即半球的下表面处并不与液体接触,
但这并不改变半球上表面受液体压力作用的情况,
则液体本身对半球的压力为F上=πr2ρgH﹣ρgπr3,
本题中要考虑大气压,大气压作用在液体上,且液体能传递压强,
则实际上液体对半球的压力为F上′=πr2ρgH﹣ρgπr3+p0πr2;
(2)半球刚要被拉起时,容器底板对半球的下表面已无向上的支持力,
则竖直向上的拉力F拉至少要等于上述的F上、半球本身的重力、大气压力之和,
即:F拉=F上+mg+p0S=πr2ρgH﹣ρgπr3+mg+p0πr2。
故答案为:πr2ρgH﹣ρgπr3+p0πr2;πr2ρgH﹣ρgπr3+mg+p0πr2。
26.【分析】(1)分析图示情景,找出浮力与物体排开液体体积的关系,然后得出结论。
(2)根据图示情景,求出浮力与物体排开液体重力的关系,然后得出结论。
(3)首先利用称重法求出乙物体受的浮力,再根据F浮=ρ水gV排求出乙物体的体积V=V排,再根据公式G=mg求出乙物体的质量,最后根据公式ρ=求出乙物体的密度。
【解答】解:(1)由图中(a)、(b)和(c)的实验可知:物体进入同种液体时,物体排开水的体积越大,物体受到的浮力越大。
(2)由图(d)和(e)所示实验可知:乙物体受的浮力F乙=G﹣F拉=5N
浮力综合作业三之拔尖篇(难度大)
一.选择题(共20小题)
1.三个完全相同的长方体木块,把它们分别放在三种密度不同的液体里,木块静止时浸入液体的情况是:甲木块大部分浸入;乙木块一半浸入;丙木块小部分浸入,如图所示。若将三木块露出液面部分切除后,剩下部分分别放入原容器中,则木块露出液面部分的体积( )
A.甲最多 B.乙最多 C.丙最多 D.一样多
2.一实心小球分别放入装有足量的水、酒精的容器中时,所受的浮力分别为0.9牛、0.8牛,已知酒精的密度为0.8×103千克/米3.则小球的密度为( )
A.0.8×103千克/米3 B.0.9×103千克/米3
C.1.0×103千克/米3 D.缺少条件,无法计算
3.一个充气的气球下面挂一个金属块,把它们放入水中某处恰能悬浮,如图所示。如果轻轻触碰一下气球,则金属块和气球( )
A.仍能静止 B.向下运动 C.向上运动 D.都有可能
4.甲、乙两个完全相同的烧杯,装满水放在水平桌面上。将体积相同的两个小球A、B分别放在甲、乙烧杯中,小球静止时如图所示。甲、乙两杯水对容器底的压强分别为p甲和p乙,A、B两个小球受到的浮力分别是FA和FB,容器底部受到的压力为F1和F2,容器对桌面的压力分别为F甲和F乙,则下列判断中正确的是( )
A.p甲>p乙 B.FA>FB C.F1=F2 D.F甲<F乙
5.如图所示,在图甲中,用细线将一实心铁球浸没在水中静止,图乙中将一实心铜球浸没在煤油中静止。铁球所受重力为G铁;体积为V铁;铜球所受重力为G铜,体积为V铜。铁球和铜球所受细线的拉力大小相等,所受浮力分别为F铁和F铜,已知水的密度为ρ水,煤油的密度为ρ油,且ρ油<ρ水<ρ铁<ρ铜,则下列判断正确的是( )
A.V铜=V铁 B.V铜>V铁 C.F铜=F铁 D.F铜<F铁
6.如图,在水平桌面上,放有一个底面积为100cm2且高10cm的柱形容器,装有6cm深的水。现用细线吊着一个密度为0.6g/cm3,高10cm,横截面积为50cm2的实心物体A(不吸水);使物体A的下表面恰好与水面接触,容器的重力忽略不计,则下列说法正确的是( )
A.物体A的重力为0.3N
B.要使细线的拉力为0,A应竖直向下移动6cm
C.若用细针将A压入水中浸没,此时容器对桌面的压力为9N
D.若物体吸水,将A缓慢浸入水中,最终物体A漂浮且露出2cm,此时水对容器底的压强为900Pa
7.八中物理实验社团设计了顶部开有小孔的水库自动泄洪控制装置模型,如图所示。其中A为压力传感器,B是不吸水的圆柱体,能沿固定的光滑细杆在竖直方向自由移动。当模型内水深h1=15cm时,B与模型底面刚好接触且压力为零。水面上涨到设计的警戒水位时,圆柱体对压力传感器的压力为3N,触发报警装置,开启泄洪阀门。已知圆柱体B的底面积SB=100cm2,高hB=25cm,下列说法正确的是( )
①圆柱体B的密度0.6g/cm3
②刚触发报警装置时,B浸入水中的深度h2为12cm
③为了提高防洪安全性,使警戒水位比原设计低9cm,可在B的上方加上与B底面积相同、高为15cm、密度为0.4g/cm3的圆柱体C
④为了提高防洪安全性,增加圆柱体B高度为35cm,可使警戒水位比原设计低4cm
A.①③ B.②③ C.①④ D.①③④
8.有一重为2N的金属圆筒,口朝上放入水中时有的体积露出水面,如果在筒中倒入5×10﹣5m3的某种液体后,圆筒有体积露出水面,则筒内液体的密度是( )
A.1.2×103kg/m3 B.1.0×103kg/m3
C.2.0×103kg/m3 D.0.8×103kg/m3
9.如图所示,薄壁圆柱体容器的上半部分和下半部分的底面积分别为20cm2和30cm2,高度都为11cm,用轻杆连接一个不吸水的长方体放入容器中,长方体的底面积为15cm2、高为10cm,长方体的下表面距离容器底部始终保持6cm,现往容器内加水,当加入0.24kg和0.27kg水时,杆对长方体的作用力大小相等,(ρ水=1.0×103kg/m3,g取10N/kg)则长方体的密度为( )
A.0.6 g/cm3 B.0.7 g/cm3 C.0.9 g/cm3 D.1.1 g/cm3
10.如图所示,甲图中圆柱形容器中装有适量的水。将密度均匀的木块A放入水中静止时,有的体积露出水面,如图乙所示,此时水对容器底部的压强比图甲水对容器底部的压强增加了300Pa.若在木块A上表面轻放一个质量为m1的物块,平衡时木块A仍有部分体积露出水面,如图丙所示,此时水对容器底部的压强比图甲水对容器底部的压强增加了400Pa.若将容器中的水换成另一种液体,在木块A上表面轻放一个质量为m2的物块,使平衡时木块A露出液面部分与丙图相同,如图丁所示。若m1:m2=5:1,则下列说法中错误的是( )
A.木块A的质量mA与m1之比为1:3
B.在丁图中,液体的密度为0.8×103kg/m3
C.木块A的密度为0.6×103kg/m3
D.在图丙中,木块A露出水面的体积与木块A的体积之比是1:5
11.如图甲所示,一个柱形容器放在水平桌面上,容器中立放着一个底面积为100cm2,高为12cm,质量为900g的均匀实心长方体木块A,A的底部与容器底用一根细绳(细绳体积忽略不计)连在一起,已知细绳长度为L=8cm。现慢慢向容器中加水,当加入1.8kg的水时,木块A对容器底部的压力刚好为0,如图乙所示,若继续缓慢向容器中加水,直到细绳被拉断,然后停止加水,如图丙所示,细绳拉断前、后木块静止时,水对容器底部压强的变化量为50Pa,(整个过程中无水溢出),则下列说法正确的是( )
A.木块A的密度为7.5×103kg/m3
B.容器的底面积为200cm3
C.细绳拉断前物体所受到的浮力为10N
D.最后容器中水的总质量为4.5kg
12.如图所示,弹簧上端与物块m相连接,下端固定在容器底部。当物块浸没在水中静止时与浸没在酒精中静止时,弹簧的弹力大小相等。物块的体积为100cm3,酒精的密度为0.8×103kg/m3(不计弹簧质量及体积)其中正确的是( )
A.物块浸没在水中静止时弹簧对底部的拉力为0.2N
B.当弹簧脱离容器底部后静止时物块露出水面的体积为物块体积的
C.物块浸没在酒精中静止时弹簧对物块的支持力是0.1N
D.物块的质量为0.9kg
13.如图所示,甲图中圆柱形容器中装有适量的水,将密度均匀的木块A放入水中静止时,有的体积露出水面,如图乙所示,此时水对容器底部的压强比图甲水对容器底部的压强增加了300Pa。若在木块A上表面轻放一个质量为m1的物块,平衡时木块A仍有部分体积露出水面,如图丙所示,此时水对容器底部的压强比图甲水对容器底部的压强增加了400Pa。若将容器中的水换成另一种液体,在木块A上表面轻放一个质量为m2的物块,使平衡时木块A露出液面部分与丙图相同,如图丁所示。若m1:m2=5:1,水的密度为1.0×103kg/m3。则下列说法中正确的是( )
A.木块A的质量mA 与m1 之比为1:3
B.木块A的密度为0.4×103kg/m3
C.在图丙中,木块A露出水面的体积与木块A 的体积之比是1:6
D.图丁中的液体密度为0.8g/cm3
14.如图所示装置,实心铝块(ρ铝=2.7g/cm3)B、C的体积均为10cm3,当B浸没在水中时,木块A恰能在粗糙的水平桌面上向左做匀速运动,若用铝块D替换C,则A在粗糙的桌面上向右做匀速运动,则D的质量为( )(已知水的密度为1.0×103kg/m3,铝B始终在水中,水与B之间的粘滞阻力及滑轮的摩擦均忽略不计)
A.2.7g B.7g C.4.7g D.2g
15.图中容器内盛有水,一块冰包有小木块和铁钉,漂浮于水面。当冰全部熔解(熔化)后,水面的高度将( )
A.升高 B.不变
C.下降 D.以上情形都可能发生
16.一个底面积为300cm2的柱形薄壁水槽放在水平台面上,用原长为10cm的弹簧将上方开口的A杯与水槽底部相连,A杯为薄壁容器,重为4N,底面积为100cm2。向水槽中加水,当A杯浸入深度为8cm时,水面如图甲所示。若再向A杯中加水,当水槽液面恰好与A杯口相平时停止加水,如图乙所示,此时弹簧对A杯的作用力大小与甲图中弹簧对A杯的作用力大小相等。已知弹簧每受1N的拉力时弹簧伸长0.5cm,不计弹簧的重力、体积及其所受的浮力。下列说法正确的是( )
①甲图中弹簧对A杯施加了竖直向下的拉力为4N
②与甲图相比,乙图中A杯向下移动的距离为2cm,水面上升1cm
③与甲图相比,乙图中水槽对桌面的压力增加了6N
④乙图中,打开阀门B,待水静止后,水对槽底的压强为2200Pa
A.①② B.②③ C.①④ D.①③
17.如图所示,甲图中圆柱形容器中装有适量的水,将密度均匀的木块A放入水中静止时,有的体积露出水面,如图乙所示,此时水对容器底部的压强比图甲水对容器底部的压强增加了300Pa.若在木块A上表面轻放一个质量为m1的物块,平衡时木块A仍有部分体积露出水面,如图丙所示,此时水对容器底部的压强比图甲水对容器底部的压强增加了400Pa.若将容器中的水换成另一种液体,在木块A上表面轻放一个质量为m2的物块,使平衡时木块A露出液面部分与丙图相同,如图丁所示。若m1:m2=5:1,水的密度为1.0×103kg/m3.则下列说法中正确的是( )
A.木块A的质量mA与m1之比为1:3
B.木块A的密度为0.6×103kg/m3
C.在图丙中,木块A露出水面的体积与木块A的体积之比是1:6
D.图丁与图甲比较,液体对容器底部的压强增加了320Pa
18.小明设计了如图甲所示的装置测量液体密度,不吸水的实心圆柱体A的高度h0=40cm,上表面与容器中的水面刚好相平,下表面与圆柱形容器底的距离h1=20cm,压力传感器可以显示物体B对其支撑面压力F的大小。现以400cm3/min的速度将水匀速抽出,40min恰能将水全部抽尽,压力传感器示数F随时间t变化的图象如图乙所示。已知圆柱形容器底面积S=400cm2,轻质细线无弹性但承受的拉力有一定限度。(忽略摩擦)下列说法正确的是( )
A.物体B所受的重力是120N
B.物体A的密度为1.6×103kg/m3
C.当绳子拉断时,压力传感器的示数为60N
D.改变圆柱形容器中的液体,使物体A浸没在液体中,用压力传感器的示数显示液体密度的大小,则此密度测量仪的测量范围为0.5×103kg/m3~2.0×103kg/m3
19.在一足够高的容器底部固定一轻质弹簧,弹簧原长10cm,弹簧上方连有正方体木块A,木块的边长为10cm,容器的底面积为200cm2,如图,此时弹簧长度为6cm(已知弹簧的长度每改变1cm,所受力的变化量为1N),现向容器内注入某种液体,当木块A有的体积浸入液体中时,弹簧恰好处于自然伸长状态;在木块A正上方放置一合金块B,静止时液面刚好浸没B,已知合金块的体积为100cm3,高为4cm。下列说法中不正确的是( )
A.木块A的重力为4N
B.液体的密度为0.8×103kg/m3
C.放置合金块B后液体对容器底部的压强为1440Pa
D.合金块B的重力为14.8N
20.如图所示,一边长为10cm的实心正方体塑料块挂于弹簧测力计正下方,此时弹簧测力计读数为5N,此时塑料块下方刚好与水面接触,且距底面积为300cm2的容器底部5cm,现往容器中缓慢加水,已知弹簧的形变量与受到的拉力成正比,即弹簧受到1N的拉力时伸长1cm。以下说法正确的是( )
A.塑料块的密度为5g/cm3
B.当加入1000cm3水时,正方体物块所受浮力为5N
C.当加入3000cm3水时,水对容器底的压强为1500Pa
D.当加水至塑料块刚好漂浮时停止加水,然后将容器内的水以50cm3/s的速度向外排出,同时向上拉动弹簧测力计,使物体以1cm/s的速度向上移动,则经过约2.86s之后,弹簧测力计示数再次回到5N
二.填空题(共10小题)
21.甲、乙两个柱形容器中分别盛有密度为ρ1、ρ2的液体。A、B是两个实心正方体,密度为ρA、ρB,所受的重力为GA、GB,体积为VA、VB,将A和B以不同的方式先后放入甲、乙两容器的液体中,如图所示。在甲容器中,A有的体积露出液面。在乙容器中,A、B通过细绳相连,B受到容器底的支持力为F支(B与容器底不密合),受到细绳的拉力为F拉。不计细绳的质量和体积,ρ1:ρ2=2:1,VA:VB=4:1,F支:F拉=1:3,则ρA:ρB= 。
22.在抗震救灾中,某舟桥部队利用冲锋舟为灾区开辟了水上生命线。人们乘坐的冲锋舟满载时排开水的体积是1.5m3,冲锋舟自重为0.6×104N,假设每人的平均质量为60kg。则:
(1)冲锋舟满载时所受的浮力是 N;
(2)为保证安全,这条冲锋舟最多能承载 人;
(3)冲锋舟底部0.5m深处所受水的压强 Pa.(g=10N/kg)
23.如图甲所示,装有部分水的试管竖直漂浮在容器内的水面上,试管内水面与容器底部的距离为h,试管壁的厚度不计,粗细均匀。现将某物块放入试管,物块漂浮在试管内的水面上,试管仍漂浮在容器内的水面上,此时试管内水面与容器底部的距离为h',如图乙所示,则h′ h(选填“>”“<”或“=”)。取走该物块,将另一物块完全浸没在该试管水中,发现试管内水面与容器底部的距离恰好又变为h,如图丙所示,若试管横截面积与容器横截面积之比为1:n,则新放入物块密度为 g/cm3。若外容器装的是盐水,内试管装的是纯水,放入另一物块仍满足液面高度h不变,则该新物块的密度又是 g/cm3。( )
24.利用一根吸管制作一个简易密度计
(1)为了让饮料吸管能竖直的漂浮在液体中,应在吸管的 (上端/下端)塞入一些铜丝作为配重,并用石蜡将吸管的下端封闭起来。若将它放入液体中后不能竖直漂浮,请提出改进做法 。
(2)这根吸管竖直漂浮在不同液体中时,液体的密度越大,它露出液面部分的长度 (越长/越短/不变),受到的浮力大小 (变大/变小/不变)。
(3)通过正确计算,在吸管上标出对应的刻度线,便制成了一个简易的吸管密度计。下列四种刻度的标示合理的是
(4)为了使测量结果更准确,如何使简易密度计上两条刻度线(如0.9、1.0)之间的距离大一些?写出一种方法。 。
25.如图所示,一根细绳悬挂一个半径为r、质量为m的半球,半球的底面与容器底部紧密接触,此容器内液体的密度为ρ,高度为H米,大气压强为p0,已知球体的体积公式是V=,球面积公式是S球=4πr2,圆面积公式是S圆=πr2.则液体对半球的压力为 。若要把半球从水中拉起,则至少要用 的竖直向上的拉力。
26.小华同学为了探究物体浸在水中所受浮力的有关规律。他将甲物体分别按如图(a)、(b)、(c)所示浸在水中;接着他将乙物体浸没在水中如图(d)所示:又将丙物体浸没在水中如图(e)所示,请根据实验现象和相关结论归纳得出结论:
(1)分析图(a)、(b)、(c)的实验,可初步得出结论
(2)分析图(d)、(e)的实验,可初步得出结论
(3)小华发现由图(d)、(e)的实验还可以计算出乙物体和丙物体的密度,则乙物体的密度为 。
27.如图甲,足够高的圆柱形容器,高处有一个注水口以10cm3/s速度均匀向该容器内注水,在容器正上方的天花板上,有一轻质细杆(体积忽略不计)粘合着由两个横截面积不同的实心圆柱体组成的组合工件,A、B的密度相同,图乙中的坐标记录了从注水开始到注水结束的1min内,水面高度h的变化情况。已知t1=14s和t2=58s时,杆对圆柱体组合工件的作用力之比为2:3,则A、B的密度为 kg/m3。
28.资料显示:牛奶中掺水量越多,牛奶密度越小。小丽想通过测定密度来比较二种牛奶品质的优劣,她自制了一个可测液体密度的“浮标”﹣﹣在竹筷子下面缠绕一些铁丝,如图甲所示。
(1)纯牛奶是 (选填“纯净物”或“混合物”)。
(2)分别将“浮标”浸入A、B两牛奶中,待静止后,筷子上与液面相平的位置分别标记为A和B,如图乙所示。比较标线A和B的上下位置,可知A、B牛奶的密度为ρA ρB,由此可知A、B牛奶品质的优劣。
(3)在实际调量过程中,发现“浮标”杆上的二条标记线靠得很近,为了更易区分,请你提出一条改进“浮标”的建议 。
29.如图所示,我国首艘航母“辽宁号”的排水量为67500t,当航母满载静止在水面上时受到的浮力为 N;舰体底部在水面下10m深处受到海水的压强是 Pa(g取10N/kg,ρ水=1.0×103kg/m3)。
30.在一个底面积为200平方厘米、高度为20厘米的圆柱形薄壁玻璃容器底部,放入一个边长为10厘米的实心正方体物块,然后逐渐向容器中倒入某种液体。右图反映了物块对容器底部压力的大小F与容器中倒入液体的深度h(0~6厘米)之间的关系。
由此可知这种液体的密度大小为 千克/米3,当倒入液体的深度h为12厘米时,物块对容器的底部压力的大小F大小为 牛。
三.实验探究题(共10小题)
31.小巴同学探究“浮力的大小与物体排开水所受重力的关系”的实验装置及过程如图所示:
(1)如图A到E所示,会影响实验结论的是图 的实验装置(填字母代号);
(2)在完善实验装置后,有如下实验步骤,你认为不重复操作且排序合理的应是 ;(填字母代号)
①将铁块挂在弹簧测力计上,弹簧测力计的读数为F1
②将铁块浸没在液体中,弹簧测力计的读数为F2
③将装有排出液体的小桶挂在弹簧测力计下,弹簧测力计读数为F3
④将空桶挂在弹簧测力计下,弹簧测力计读数为F4
A.①②③④
B.①④②③
C.④①②③
D.④②①③
(3)通过探究,若等式 成立(选用F1、F2、F3和F4表示),则得出阿基米德原理;
(4)为了得到更普遍得结论,下列继续进行的操作中不合理的是 ;(填字母代号)
A.用原来的方案和器材多次测量取平均值
B.用原来的方案将水换成酒精进行实验
C.用原来的方案将石块换成体积与其不同的铁块进行实验
(5)小蜀同学在图C的操作中,只将石块的一部分浸在水中,其他步骤操作正确,则 (选填“能”或“不能”)得到与(3)相同的结论;
(6)小鲁同学利用上述实验中的器材和木块,探究“漂浮在液面上的物体所受浮力的大小是否遵循阿基米德原理”,实验过程中不需要弹簧测力计的是图中 (填“A”“B”“C”“D”或“E”)所示步骤;
(7)小巴同学还想利用浮力测量木块的密度,他找来的实验器材有:木块、弹簧测力计(0~5N)、底部固定有滑轮的水槽、细线及足量的水:
①如图甲,先用弹簧测力计测木块的重力;再用细线绕过滑轮将木块与测力计连接起来接着往水槽中倒入适量的水,使木块浸没在水中,如图乙,木块在水中静止时测力计示数为1.6N。她利用定滑轮改变力的方向的作用,巧妙的得到了木块的密度为 kg/m3;
②实验完毕小巴收拾仪器时,发现弹簧测力计在竖直方向未使用时,指针始终指在0.1N处,则他测得的木块密度会比真实值 (选填“偏大”“偏小”或“不变”)。
32.小明按照教材中“综合实践活动”的要求制作简易密度计。
(1)取一根粗细均匀的饮料吸管,在其下端塞入适量金属丝并用石蜡封口。塞入金属丝的目的是 。
(2)将吸管放到水中的情景如图(a)所示,测得浸入的长度为H;放到另一液体中的情景如图(b)所示,测得浸入的长度为h。用ρ水、ρ液分别表示水和液体的密度,则ρ水 ρ液(选填“=”、“>”、“<”),用F水、F液分别表示吸管在水和液体中受到的浮力,则F水 F液(选填“=”、“>”、“<”),此外h与ρ水、ρ液及H的关系式为h= 。
(3)小明根据图(a)在吸管上标出1.0刻度线(单位g/cm3,下同),再利用上述关系式进行计算,标出了0.8、0.9、1.1、1.2的刻度线(图中未画出)。结果发现,1.1刻线在1.0刻线的 (选填“上”、“下”)方,相邻刻线的间距 (选填“均匀”、“不均匀”)。
(4)为检验刻度误差,小明取来食油,先用天平和量筒测量其密度,然后再用这个密度计测量。但操作时却出现了图(c)所示的情形,这让他很扫兴。难道实验就此终止了吗,根据经验或思考,在不更换食油的情况下,你认为可以进行怎样的尝试: 。
33.利用一根吸管制作一个简易密度计
(1)为了让饮料吸管能竖直的漂浮在液体中,应在吸管的下端塞入一些铜丝作为配重,并用石蜡将吸管的下端封闭起来。若将它放入液体中后不能竖直漂浮,请提出改进做法 。
(2)这根吸管竖直漂浮在不同液体中时,液体的密度越大,它露出液面部分的长度 (越长/越短/不变),受到的浮力大小 (变大/变小/不变)
(3)通过正确计算,在吸管上标出对应的刻度线,便制成了一个简易的吸管密度计。下列四种刻度的标示合理的是 。
(4)为了使测量结果更准确,如何使简易密度计上两条刻度线(如0.9、1.0)之间的距离大一些?写出一种方法。
34.在课外实践活动中,某物理实验小组利用一根饮料吸管制作了简易密度计,如图1所示。
(1)该简易密度计应用到的物理原理有 。(从力学角度分析,填写一种即可)
(2)应在吸管的 (选填“上端”或“下端”)塞入适当的物体作为配重,然后用石蜡将吸管的下端封闭起来,使饮料吸管能竖直的漂浮在液体中。
(3)吸管竖直漂浮在不同液体中时,液体的密度越大,它露出液面部分的长度 ,受到的浮力大小 (均选填“增大”、“减小”或“不变”)。
(4)通过正确计算,在吸管上标出对应的刻度线,便制成了一个简易的吸管密度计。图2四种刻度的标示合理的是 。
(5)为了使测量结果更准确,便要使简易密度计上两条刻度线(如0.9、1.0)之间的距离大一些,请写出一种改进方法 。
35.学习浮力知识后,小华想制作一个密度计,他制作步骤如下:
a、取一根饮料吸管,将一些铁丝从吸管的下端塞入作为配重,并用石蜡将吸管的下端封起来。
b、将其漂浮在水中,在吸管上标出水面的位置,测出该位置到吸管下端的距离,即吸管浸入水中的深度H=5cm.如图所示。
c、推导:设吸管横截面积为S,在水中漂浮,故浮力与重力二力平衡,所以G=ρ水gSH;若漂浮在其它液体中,则浸入的深度h会因液体密度的改变而改变,但浮力仍与重力平衡,即G=ρ液gSh。
d、根据以上推导的公式,可计算出液体密度与下表中的密度相等时,简易密度计浸入的深度h(取密度的单位为g/cm3)
e小华做了五次实验,获得的数据如下:
实验次数 1 2 3 4 5
液体密度ρ/(g cm﹣3) 0.8 0.9 1.0 1.1
浸入的深度h/(cm) 6.3 5.6 5 4.5 4
(1)小华制作密度计的原理是利用了物体漂浮在液面时,浮力 重力(选填“大于”、“小于”或“等于”).步骤a中,将一些铁丝从吸管的下端塞入作为配重是为了降低吸管的 ,从而让它能够竖直的漂浮在液面上。
(2)通过对步骤c的分析,请推导出漂浮在ρ液液体中时,浸入深度h= (用ρ水、ρ液、H表达).在第5次试验中,观察到该密度计浸入某种液体的深度是4cm,则该液体的密度是 千克/米3
(3)分析表中数据或制作的密度计发现:简易密度计浸入液体的深度越大,表明液体的密度 (填“越大”“越小”“不变”),密度计的刻度线分布 (“是”或“不是”)均匀的。
(4)制作完毕后,小华分别测量可乐、色拉油等液体的密度,发现色拉油的密度在1.1和1.2之间,且两刻度线的距离较小,请提出一个方法使两条刻度线之间的距离大一些,使测量结果更精确。方法 。
36.为了研究物体漂浮在水面上时的特点,某小组同学用甲、乙两种材料制成体积不同的若干块物块进行实验,甲材料的密度为ρ甲,乙材料的密度ρ乙,且ρ甲<ρ乙.如图所示,他们让物块漂浮在水面上,测量并记录了物块的总体积和露出水面的体积,并将实验数据记录在下表中。
材料 实验 物块体积 露出水面体积 材料 实验 物块体积 露出水面体积
序号 (10﹣6米3) (10﹣6米3) 序号 (10﹣6米3) (10﹣6米3)
甲 1 10 6 乙 6 8 1.6
2 20 12 7 10 2
3 30 18 8 30 6
4 40 24 9 35 7
5 50 30 10 45 9
①分析比较实验序号 数据,可得出的初步结论是:同种材料的物块漂浮在水面上时,物块露出水面的体积与物块的体积成正比。
②分析比较实验序号1与7、3与8的数据,可得出的初步结论是: 。
③他们分别分析了“露出水面的体积”和“物体体积”的比例关系,可以得出的进一步结论是:
(a) 。
(b) 。
37.小明在生活中发现木块总浮在水面上,铁块却沉入水底,由此他提出两个问题:
问题1:浸入水中的铁块是否受到浮力?问题2:浮力大小与哪些因素有关?为此他做了进一步的猜想,设计并完成了如图所示实验。
(1)(b)(c)图中弹簧测力计示数均小于(a)图中弹簧测力计示数,说明浸入水中的铁块 (选填“受到”或“不受到”)浮力;
(2)做 (选填字母)两次实验,是为了探究铁块浸没在水中时所受浮力大小与深度是否有关;
(3)做(d)(e)两次实验,是为了探究浮力大小与 的关系。
38.小明同学用如图所示的实验器材和步骤,做了“验证阿基米德原理”的实验,
(1)该实验目的是:研究浸没在液体中的物体所受浮力与它排开液体 之间的关系。
(2)实验步骤有所遗漏,遗漏的步骤为 ,若将遗漏的步骤标注为E,则正确的实验步骤依次为 (填写实验步骤对应的字母)。
(3)实验中所测浮力的大小为 N,它应与 是相等的。
39.如图所示,在“探究影响浮力大小的因素”的实验中,物体A重为4N。
(1)弹簧秤读数时,视线应与刻度盘 。
(2)物体A在水中受到的浮力为 N。
(3)物体B的体积与A相同。则B所受重力为 N。
(4)图丙中液体的密度为 kg/m3。
40.阅读以下材料,回答相关问题。
我国国产第一艘航母
2017年4月26日,我国第一艘国产航母正式出坞下水。一瓶香槟酒摔碎舰艏,两舷喷射绚丽彩带,周边船舶一起鸣响汽笛,按照国际惯例举行“掷瓶礼”之后,国产航母缓缓移出船坞,停靠码头。这历史性的一刻,被定格为永恒的民族记忆,彰显着中国国家整体力量的提升。阳光下国歌声雄壮嘹亮,舰舷上五星红旗迎风招展。如果说现代文明由海洋文明开启,那么航母则是现代海军的标配,是一个民族海洋力量的象征。正因此,建设国产航母,不仅是捍卫国家利益、维护海洋权益、开发海洋文明的重要举措,更是中华民族几代人念兹在兹的百年梦想,是强军梦、强国梦的重要组成部分,寄托着中国人的民族情感。下水现场,不少人慕名而来、驻足观看;网络上,网友点赞“展示了中国速度、中国力量、中国智慧”;电视节目中,有嘉宾谈到海军发展历程喜极而泣…这个土生土长的“国之重器”,激荡着亿万人民内心深处的民族自信和爱国情怀。我们可以自豪地说:“我们已经拥有了两艘航母!”
图1是我国的“辽宁号”航母训练时的场景,图2是我国国产的第一艘航母建成下水的场景,下面是这两艘航母的一些相关参数:
“辽宁号”舰长304.5米,吃水线长270米,舷宽75米,吃水线宽:38米,吃水10.5米。标准排水量55000吨,满载排水量68000吨,最大航速32节。国产第一艘航母(暂时没有相关确切数据,大致搜集而成):舰长325米,甲板宽76.8米,吃水11米,标准排水量65000吨,满载排水量86000吨。
(1)2017年4月26日,这个日子是每一个中国人值得骄傲和自豪的,原因是
(2)我国的海军力量逐步壮大,航母从无到有,从有到多,体现了我国
(3)请你估算出我国国产航母的标准排水量,并写出合理的估算方法。
四.计算题(共20小题)
41.用同种金属材料做成A、B两个空心球,金属材料密度为2.5g/cm3,A球质量mA=1.037kg,B球质量mB=0.61kg。外径分别为RA=7cm,RB=5cm。两球空腔之间用一根金属导管相连,由于导管较细,故若施加过大的拉力会发生断裂。向A球空腔中注入300mL水,并在A、B两侧接上导线,连入一个报警电路(图中未画出)后横置于待监测液体表面。密度监测仪要求液体密度不得低于1.22g/cm3。该电路若检测到电流明显降低则触发报警。(球体体积计算公式为V=πr3,其中r为球体半径。为方便计算,可取π=3,g=10N/kg,忽略导管的重力与浮力,两侧导线始终松弛)同学们进行了下列研究:
(1)分别求出A装置和B装置的平均密度;(结果保留小数点后2位);
(2)若要保证装置准确报警,则导管所能承受的力需要满足什么条件?
(3)若此时液体的密度恰好低于1.22g/cm3,则与报警前相比,报警后A球在液面以上的体积如何变化?变化了多少?(假设报警后空腔内的水不会泄漏,以立方厘米为单位,结果保留到整数位)
42.小宁为了研究浸在液体中的物体所受浮力的规律,他设计了如图所示的实验。他将弹簧测力计一端固定,另一端挂边长为10cm正方体合金块A,放入底面积为300cm2装有水的圆筒形容器中,开始他将合金块A恰好浸没在水中,容器侧面的底部有一由阀门B控制的出水口,实验时,打开阀门B缓慢放水,放到弹簧测力计的读数不再变化时,立即关闭阀门B,在此过程中金属块始终不与容器底部接触,读出弹簧测力计示数的最小值和最大值分别为22N和32N,已知弹簧测力计每一牛顿刻度间的距离为1cm.求:
(1)在原图上作出关闭阀门B后水面的大致位置
(2)合金块A的重力及受到的最大浮力及其密度;
(3)从容器中排出水的质量。
43.如图所示,水平桌面上的圆柱形容器A的底面积为50cm2,中间自由的放入一个质地均匀的长方体物块B,物块B质量mB=160g、密度ρB=0.8×103kg/m3、底面积SB=20cm2,求:
(1)物块B对容器底部的压强。
(2)若沿器壁向A缓慢注入h=5cm深的水后,B将受到多大的浮力?
(3)向A缓慢注入质量为多克的水后,B对容器底的压力减小为零?
44.如图甲所示,水平面上有一底面积为5.0×10﹣8m2的圆柱形薄壁容器,容器中装有质量为0.5kg的水。现将一个质量分布均匀、体积为5.0×10﹣5m3的物块(不吸水)放入容器中,物块漂浮在水面上,物块浸入水中的体积为4.0×10﹣5m3。(g取l0N/kg,水的密度ρ水=1.0×103kg/m3)
(1)求物块受到的浮力大小。
(2)求物块的密度。
(3)如图乙用力F缓慢向下压物块使其恰好完全浸没在水中(水未溢出),求F大小。
45.水平桌面上放有一底部有水阀的圆柱形容器,容器重3N,底面积为250cm2,高10cm,在容器内装入部分水,将一个边长为10cm、密度为0.6g/cm3的正方体木块用细线悬挂在水中,如图(甲)所示,木块静止时有4cm浸入水中,求:
(1)此时木块所受的浮力为多少N?
(2)细线能承受的最大拉力为5N,打开水阀放水,绳子断开时水深7cm,如图(乙),立刻关闭水阀,木块漂浮静止时,水对容器底的压强为多少Pa?
(3)在(2)操作木块漂浮静止后,再用压力F作用在木块顶部将木块下压,如图(丙),求:当木块对容器底部压强为200Pa时,容器对桌面的压强为多少Pa?
46.一块浮冰浮在海面上,露出海面体积5m3.一质量为800kg的北极熊想爬到浮冰上捕食海豹,问:
(1)北极熊能否趴在冰面上?(取ρ海水=1.0×103kg/m3ρ冰=0.9×103kg/m3)
(2)整块浮冰质量多大?
47.如图所示,A、B是两个完全相同的容器,底面积为100cm2,分别盛有适量的煤油和水,置于水平桌面上。现将一实心小球分别放入A、B两容器中,小球静止后排开煤油和水的体积分别为20cm3和18cm3,求:
(1)小球在煤油中受到的浮力;
(2)小球的密度。(ρ煤油=0.8×103kg/m3,小球放入容器中均无液体溢出)。
48.一块质量为1.2kg的木块浮在水面上,它的密度是0.6×103kg/m3,木块漂浮在水面上时,受到的浮力是多大?要把木块全部浸入水中,至少需要加多大竖直向下的压力?
49.如图所示,已知重为10N的长方体木块静止在水面上,浸入在水中的体积占木块总体积的(g取10N/kg)。
(1)求木块所受浮力;
(2)若木块下表面所处的深度为0.2m,求木块下表面受到水的压强;
(3)求木块下表面面积;
(4)若要将木块全部浸没水中,求至少需要施加多大压力。
50.某物体的质量为2kg,体积为 3×10﹣3 m3.将其浸没在水中,g=10N/kg:
(1)此时物体受到多大的浮力?
(2)松手后,该物体是上浮,还是下沉?(计算说明)
(3)物体静止时,受到多大的浮力?(说明必要的理由)
51.在标准大气压下,将一质量是20克长15厘米的平底试管倒扣放在水中,试管的底面积为300毫米2,试管受到的浮力是多大?上面再放一质量是4克的物体,试管底刚好与水面相平,试管中水柱是多少厘米?试管内空气柱压强为多大?(不计空气的质量)
52.将边长是10cm的实心立方体木块轻轻地放入盛满水的大水槽内,待木块静止时,从水槽中溢出了600g水,取g=10N/kg,
求:(1)木块受到的浮力
(2)木块的重力
(3)若木块没入水中,它受的浮力。
53.如图甲所示,A、B为不同材料制成的体积相同的实心正方体,浸没在盛有水的薄壁圆柱形容器中,容器底面积是正方体下表面积的4倍,现在沿竖直方向缓慢匀速拉动绳子,开始时刻,A的上表面刚好与水面相平,A、B之间的绳子绷直,B在容器底部(未与容器底部紧密接触),A上端绳子的拉力是F,F随A上升的距离h变化的图像如图乙所示,除了连接A、B间的绳子承受拉力有一定限度外,其它绳子不会被拉断,绳的质量和体积忽略不计,求:
(1)正方体A的体积;
(2)正方体B的密度;
(3)整个过程中,水对容器底部压强的最小值。
54.如图甲所示,水平面上有一底面积为5.0×10﹣3m2的圆柱形薄壁容器,容器中装有质量为0.5kg的水,现将一个质量分布均匀、体积为5.0×10﹣5m3的物块(不吸水)放入容器中,物块漂浮在水面上,物块浸入水中的体积为4.0×10﹣5m3.(g取10N/kg,水的密度ρ水=1.0×103kg/m3)。
(1)求物块受到的浮力大小;
(2)求物块的密度;
(3)用力缓慢向下压物块使其恰好完全浸没在水中(水未溢出)如图乙,求该力F的大小。
55.如图是湖南师范大学学生发明的水上自行车,车下固定5个充满气的气囊,每个气囊的体积均为3.0×10﹣2m3,已知该水上自行车的总质量为25kg,不计车轮浸入水中的体积。(g取10N/kg)
(1)当自行车停放在水面上没人骑行时,气囊排开水的总体积为多少?
(2)当质量为75kg的人骑行时,固定在正中间的1个气囊破裂,该自行车是否还能安全骑行?请通过计算说明。
56.如图甲所示,一个柱形容器放在水平桌面上,容器中立放着一个底面积为100cm2,高为12cm均匀实心长方体木块A,A的底部与容器底用一根细绳连在一起,现慢慢向容器中加水,当加入1.8kg的水时,木块A对容器底部的压力刚好为0,如图乙所示,此时容器中的水的深度为9cm。已知细绳长度为L=8cm,ρ水=1.0×103kg/m3.求:
(1)当木块A对容器底部的压力刚好为0,A受到的浮力;
(2)木块A的密度;
(3)若继续缓慢向容器中加水,当容器中的水的总质量为4.5kg时,停止加水,如图丙所示,此时将与A相连的细绳剪断,求细绳剪断前、剪断后木块静止时,水对容器底部压强的变化量。(整个过程中无水溢出)
57.宋朝的怀丙和尚利用船的浮力打捞万斤的铁牛,如图甲,受此启发,小李同学设计了如图乙利用浮力打捞物品的装置。乙图所为一个足够高的柱形容器,待打捞物体A质量为1.5kg,底面积为100cm2,高10cm;浮体B质量为1kg,底面积为200cm2,高为10cm,A、B 正中央用一个不计质量和体积的弹簧相连。已知弹簧原长为10cm,弹簧每受到1N的拉力会伸长0.5cm。
(1)浮体B的密度是多少;
(2)当柱状容器里面加水,直到弹簧处于原长时,B物体排开水的体积是多少?
(3)继续加水直到A物体刚好离开容器底部时停止,这时水对容器底的压强比弹簧处于原长时增加多少?
58.悬浮在海水中的潜艇排开海水的质量为3×106kg(g=10N/kg,海水的密度取1×103kg/m3).求:
(1)潜艇排开的海水所受重力?
(2)潜艇所受浮力多大?
(3)潜水艇排开海水的体积?
(4)处于水下150m深度处有一个面积为2.4m2的舱盖,求它所受海水的压强和压力各是多大。
浮力综合作业三之竞赛篇(难度大,只适合优等生)
参考答案与试题解析
一.选择题(共20小题)
1.【分析】(1)物体漂浮时,露出液面部分的体积占总体积的比例是由物体的密度和液体的密度共同决定的,物体和液体的密度不变,露出液面部分的体积占总体积的比例也不变。
(2)因为甲木块大部分浸入;乙木块一半浸入;丙木块小部分浸入,所以可以假设甲木块有的体积浸入;乙木块有的体积一半浸入;丙木块有的体积浸入。
【解答】解:设长方体木块的体积为V,则将木块露出液面的部分切除后:
图中甲木块的体积为V浸入,木块再次露出液面部分的体积仍为现有体积的,即V甲=V×=V。
图中乙木块的体积为V浸入,木块再次露出液面部分的体积仍为现有体积的,即V乙=V×=V。
图中丙木块的体积为V浸入,木块再次露出液面部分的体积仍为现有体积的,即V丙=V×=V。
因为V>V,所以乙图木块再次露出液面部分的体积较大。
故选:B。
2.【分析】如果球在水中和酒精中都漂浮,则它受到的浮力都等于它的重力,即两球的浮力相同,这不符合题意,则不可能都漂浮;如果两球都浸没,设球的体积为V,则它受到的浮力之比为==,所以也不可能都浸没;故球只能在水中漂浮,在酒精中浸没。
【解答】解:小球在酒精中受到的浮力为:
F浮酒=ρ酒gV球=0.8N﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
因小球在水中漂浮,
所以小球受到的浮力和重力相等,
即:F浮水=ρ球gV球=0.9N﹣﹣﹣﹣﹣﹣﹣﹣②
联立①②两式可得:
ρ球=ρ酒=×0.8×103kg/m3=0.9×103kg/m3。
故选:B。
3.【分析】(1)气球在水中的深度不同、受压强不同、体积不同、排开水的体积不同、受到的浮力就要发生变化;
(2)气球和金属块的总重不变,根据物体的浮沉条件分析判断。
【解答】解:
原来气球和金属块悬浮在水中,F浮=G,
如果向上碰的话,由于气球受到水的压强变小、气球的体积变大,气球受到的浮力增大,大于自重,气球和金属块将向上运动;
如果向下碰的话,由于气球受到水的压强变大、气球的体积变小,气球受到的浮力减小,小于自重,气球和金属块将向下运动;
当水平碰,由于气球受到水的压强不变、气球的体积不变,气球受到的浮力不变,还等于自重,仍处于悬浮,还处于静止状态;
由以上分析和知静止、向上运动、向下运动都有可能。
故选:D。
4.【分析】A.由图可知,A、B两小球放在水中静止后,水面都与烧杯口相平,则烧杯中水的深度相等,由p=ρgh可知,水对烧杯底的压强相等;
B.根据小球静止后,A漂浮在水面,B沉在烧杯底,则VA排<VB排,由公式F浮=ρgV排可知,B球静止时受到的浮力大;
C.根据题意知,容器底部受到的压力等于剩余水的重力加上球的重力,甲杯A球漂浮,GA=F浮=G排,其对容器底的压力等于满杯水的重力;乙杯B球沉底,F浮=G排<GB,其对容器底的压力大于满杯水的重力;
D.根据阿基米德原理可知,判断出小球排开水受到的重力的大小关系,由容器对桌面的压力F=G容+G水﹣G排水+G球,比较出容器对桌面压力的大小关系。
【解答】解:A.由图可知,A、B两小球放在水中静止后,水面都与烧杯口相平,则烧杯中水的深度相等,由p=ρgh可知,水对烧杯底的压强相等,即p甲=p乙,故A错误;
B.根据小球静止后,A漂浮在水面,B沉在烧杯底,则VA排<VB排,由公式F浮=ρgV排可知,B球静止时受到的浮力大于A球静止时受到的浮力,即FA<FB,故B错误;
C.根据题意知,容器底部受到的压力等于剩余水的重力加上球的重力,甲杯A球漂浮,GA=FA浮=GA排,其对容器底的压力等于满杯水的重力;乙杯B球沉底,FB浮=GB排<GB,其对容器底的压力大于满杯水的重力,即F1<F2,故C错误;
D.根据浮沉条件和阿基米德原理得:FA=GA=GA排,FB=GB排<GB,由图可知,根据容器对桌面的压力F=G容+(G水﹣G排水)+G球可知,
F甲=G容+G水﹣GA排+GA=G容+G水,
F乙=G容+G水﹣GB排+GB>G容+G水,则F甲<F乙,故D正确。
故选:D。
5.【分析】对铁球和铜球进行受力分析,两者都受到竖直向下的重力、竖直向上的拉力和竖直向上的浮力作用,根据平衡力列出等式,再根据两者受到绳子的拉力相等列出等式,通过ρ油<ρ水<ρ铁<ρ铜,比较两者体积大小,再根据阿基米德原理判断浮力大小。
【解答】解:AB、如图甲,铁球受到竖直向下的重力G铁、竖直向上的拉力F拉和竖直向上的浮力F铁,
根据平衡力得,G铁=F铁+F拉,
如图乙,铜球受到竖直向下的重力G铜、竖直向上的拉力F'拉和竖直向上的浮力F铜,
根据平衡力得,G铜=F铜+F'拉,
因为,铁球和铜球所受细线的拉力大小相等,即F拉=F'拉,
所以,G铁﹣F铁=G铜﹣F铜,
由于铁球和铜球分别浸没在水和煤油中,
所以,ρ铁gV铁﹣ρ水gV铁=ρ铜gV铜﹣ρ油gV铜,
整理得,(ρ铁﹣ρ水)V铁=(ρ铜﹣ρ油)V铜,
由于ρ油<ρ水<ρ铁<ρ铜,
所以,ρ铁﹣ρ水<ρ铜﹣ρ油,
所以,V铁>V铜,故A和B都错误。
CD、根据阿基米德原理得,
铁球受到的浮力为:F铁=ρ水gV铁,
铜球受到的浮力为:F铜=ρ油gV铜,
因为ρ油<ρ水,V铜<V铁,
所以铜球受到的浮力小于铁球受到的浮力,即F铜<F铁,故C错误,D正确。
故选:D。
6.【分析】(1)利用重力计算公式G=mg=ρVg求得物体A的重力。
(2)要使细线的拉力为0,物体A受到的浮力等于重力,结合阿基米德原理求得排开液体的体积,进一步求得A竖直向下移动的距离和水上升的高度之和,据此求得A应竖直向下移动的距离;
(3)若用细针将A压入水中浸没,利用阿基米德原理求得A完全浸没所受的浮力,进一步求得细针对A的压力,即A对容器的压力,利用G=mg=ρVg求得水的重力,进一步求得容器对桌面的压力。
(4)若物体吸水,将A缓慢浸入水中,最终物体A漂浮,据此求得此时水对容器底的压力,利用压计算公式求得水对容器底的压强。
【解答】解:A、物体A的重力为:GA=mAg=ρAVAg=0.6×103kg/m3×10×10﹣2m×50×10﹣4m2×10N/kg=3N,故A错误;
B、要使细线的拉力为0,物体A受到的浮力等于重力,F浮=GA=3N,
结合阿基米德原理可知:==3×10﹣4m3,
A竖直向下移动的距离和水上升的高度之和为:h===0.06m=6cm,
则+=h,
,
解得V′=150cm3,
A竖直向下移动:==3cm,故B错误;
C、若用细针将A压入水中浸没,A完全浸没所受的浮力为:
F浮′=ρ水gV排′=1×103kg/m3×10×10﹣2m×50×10﹣4m2×10N/kg=5N,
细针对A的压力为:F压=F浮′﹣GA=5N﹣3N=2N,
此时溢出水的体积为V溢出=V物+V水﹣V容=50cm2×10cm+100cm2×6cm﹣100cm2×10cm=100cm3,
剩余水的体积:V剩余=V水﹣V溢出=100cm2×6cm﹣100cm3=500cm3,
容器中剩余水的重力为:
G水=m水g=ρ水V水g=1×103kg/m3×500×10﹣4m2×10N/kg=5N,
容器的重力忽略不计,容器对桌面的压力为:F=F压+G水+GA=2N+5N+3N=10N,故C错误;
D、若物体吸水,将A缓慢浸入水中,最终物体A漂浮,此时水对容器底的压力为:F′=GA+G水=3N+6N=9N,
水对容器底的压强为:p==900Pa,故D正确。
故选:D。
7.【分析】(1)根据当模型内水深h1=15cm时,根据体积公式求出B排开水的体积,根据B与模型底面刚好接触且压力为零可知B处于漂浮状态,根据阿基米德原理结合物体的漂浮条件求出B的重力,根据G=mg求出B的质量,根据密度公式求出B的密度;
(2)触发报警装置时,圆柱体B对压力传感器的压力为3N,由于力的作用是相互的,所以压力传感器对圆柱体B的压力也为3N,对B受力分析可得受到的浮力,根据F浮=ρ液gV排得B排开液体的体积,进一步求得B浸入水中的深度;
(3)根据刚触发报警装置时圆柱体对压力传感器的压力为3N结合力的平衡条件求出B受到的浮力,阿基米德原理求出B排开水的体积,根据体积公式求出B浸入水中的深度;根据刚触发报警装置时B浸入水中的深度和B的高度求出A到水面的距离,根据警戒水位需要比原设计低9cm求出此时A到水面的距离,进而表示出BC整体排开水的深度,根据体积公式和阿基米德原理表示出BC整体受到的浮力,根据体积公式、密度公式和G=mg表示出BC整体的重力,根据力的平衡条件表示出BC整体受到的浮力、圆柱体对压力传感器的压力和BC整体的重力之间的关系,解方程求出圆柱体C的高度;
(4)根据刚触发报警装置时B浸入水中的深度和B的高度求出B未增高前A到水面的距离,将圆柱体B的高度增加10cm,根据GB'=×GB可求出此时B的重力,由力的平衡条件可求出刚触发报警装置时B受到的浮力,根据阿基米德原理可求出此时B排开水的体积,从而求出此时B浸入水中的深度和A此时到水面的距离,从而求出警戒水位下降的高度。
【解答】解:①当模型内水深h=15cm时,水对容器底部的压强为
p=ρ水gh1=1.0×103kg/m3×10N/kg×0.15m=1500Pa,
此时B排开水的体积为
V排1=SBhl=100cm2×15cm=1500cm3=1.5×10﹣3m3,
由B与模型底面刚好接触且压力为零可知,此时B处于漂浮状态,由物体的漂浮条件可知,B的重力为
GB=F浮l=ρgV排1=1.0×103kg/m3×10N/kg×1500×10﹣6m3=15N,
B的密度为ρB====0.6×103kg/m3=0.6g/cm3,故①正确;
②触发报警装置时,圆柱体B对压力传感器的压力为3N,由于力的作用是相互的,所以压力传感器对圆柱体B的压力也为3N,对B受力分析可得,受到的浮力为
F浮2=G+F压=15N+3N=18N
根据F浮=ρ液gV排得,B排开液体的体积为V排2===1.8×10﹣3m3,
B浸入水中的深度为h2===0.18m=18cm,故②错误;
③由刚触发报警装置时B浸入水中的深度和B的高度可知,A到水面的距离
hA=hB﹣h2=25cm﹣18cm=7cm,
警戒水位需要比原设计低9cm时,A到水面的距离为
hA'=hA+9cm=7m+9cm=16cm,
则BC整体排开水的深度为
hBC=hC+hB﹣hA'=hC+25cm﹣16cm=hC+9cm,
BC整体排开水的体积为
VBC=SBhBC=100cm2×(hC+9cm)=(100hC+900)cm3,
此时BC整体受到的浮力为
F浮BC=ρ水gVBC=1.0×103kg/m3×10N/kg×(100hC+900)×10﹣6m3,
BC整体的体积为VBC=SB (hC+hB)=100cm2×(hC+25cm)=(100hC+2500)cm3,
由密度公式和G=mg可知,BC整体的重力为GBC=GB+GC=15N+0.4×103kg/m3×10N/kg×100×hC×10﹣6m3,
由力的平衡条件可知F浮BC=GBC+F,
代入得1.0×103kg/m3×10N/kg×(100hC+900)×10﹣6m3=15N+0.4×103kg/m3×10N/kg×100×hC×10﹣6m3+3N,
解得:hC=15cm,故③正确;
④B未增高前,A到水面的距离为hA=hB﹣h2=25cm﹣18cm=7cm,
增加圆柱体B高度为35cm,则此时B的重力为GB′===21N,
由力的平衡条件可知,刚触发报警装置时,B受到的浮力F浮3=GB′+F=21N+3N=24N,
由阿基米德原理可知,此时B排开水的体积V排3===2.4×10﹣3m3=2400cm3,
此时B浸入水中的深度h3===24cm,
此时A到水面的距离hA′=hB′﹣h3=35cm﹣24cm=11cm,
所以增加圆柱体B高度为35cm,则警戒水位比原设计低的距离为Δh′=hA′﹣hA=11cm﹣7cm=4cm,故④正确。
综上可知,D正确,ABC错误。
故选:D。
8.【分析】(1)金属筒容器有的体积露出水面,说明它漂浮,则浮力等于重力等于2N,利用阿基米德原理公式的变形公式:V排=计算出排开水的体积,然后除以就是金属筒的容积V物;
(2)利用阿基米德原理计算出金属筒有的体积没在水中时的浮力,则浮力减去金属筒的重力,就是5×10﹣4m3的某种液体的重力,然后利用公式ρ=计算液体密度。
【解答】解:(1)金属筒漂浮,F浮=G筒=2N。
∵F浮=ρ水V排g
∴V排===2×10﹣4m3,
∵的体积露出水面。
∴V筒==×2×10﹣4m3=3×10﹣4m3。
(2)装入液体后的浮力:F浮′=ρ水g(1﹣)V筒=1×103kg/m3×10N/Kg××3.0×10﹣4m3=2.4N,
装入液体后的浮力等于金属筒重力加上液体重力,所以:G液=F浮′﹣G筒=2.4N﹣2N=0.4N,
筒内液体的密度ρ====0.8×103kg/m3。
故选:D。
9.【分析】(1)首先分析加水0.24kg和0.27kg水位到达哪里。
(2)当加入0.24kg和0.27kg水时,杆对长方体的作用力大小相等,说明当加入0.24kg水时,物体受到竖直向下的重力、竖直向上的浮力和杆对物体的拉力,当加入0.27kg水时,物体受到竖直向下的重力和杆对物体向下的压力、竖直向上的浮力,物体的重力相等,根据重力相等列等式求解。
【解答】解:0.24kg=240g,0.27kg=270g
(1)如果把图中黄色部分加满,黄色部分是物体底部到容器底的部分,
h1=6cm,体积:V1=S1h1=30cm2×6cm=180cm3,加水质量:m1=ρV1=1.0g/cm3×180cm3=180g
(2)240g水剩余的质量:m2=240g﹣180g=60g,60g体积为:V2===60cm3,60g的水要加在绿色部分,
水面升高距离:h2===4cm
此时物体受到竖直向下的重力、竖直向上的浮力和杆对物体的拉力,G=F浮+F﹣﹣①
(3)继续加水,又加水270g﹣240g=30g,这30g水首先把红色部分填满,
红色部分高度:h3=11cm﹣6cm﹣4cm=1cm,红色部分的体积:V3=(S1﹣S)h3=(30cm2﹣15cm3)×1cm=15cm3,红色部分加水质量:m3=ρV3=1.0g/cm3×15cm3=15g
(4)把红色部分加满,剩余质量:m4=30g﹣15g=15g,15g水要加在蓝色部分,
蓝色部分的体积:V4===15cm3,蓝色部分的高度:h4===3cm
此时物体受到竖直向下的重力和杆对物体向下的压力、竖直向上的浮力,G=F'浮﹣F﹣﹣②
由①②得,F浮+F=F'浮﹣F,
ρ水gV排+F=ρ水gV'排﹣F,
ρ水gSh2+F=ρ水gS(h2+h3+h4)﹣F,
2F=ρ水gS(h2+h3+h4)﹣ρ水gSh2,
2F=ρ水gS(h3+h4),
2F=1.0×103kg/m3×10N/kg×15×10﹣4m2×(1+3)×10﹣2m,
解得,F=0.3N,
由①得,G=F浮+F
ρgV=ρ水gV排+F
ρ×10N/kg×15×10﹣4m2×10×10﹣2m=1.0×103kg/m3×10N/kg×15×10﹣4m2×4×10﹣2m+0.3N,
解得,ρ=0.6×103kg/m3=0.6 g/cm3
故选:A。
10.【分析】(1)设A的体积为V、容器的底面积为S,由于容器为圆柱形容器,在水中放入木块A后,A在水中漂浮,容器底受到的压力的变化值等于木块A的重力;而木块受到的浮力等于木块的重力,则压强变化值ΔP===;同理,比较甲丙图,压强变化值ΔP′==,知道ΔP、ΔP′的大小,可求丙图排开水的体积大小,进而求出木块A的质量mA与m1之比和木块A露出水面的部分占自身体积比值;
(2)在丙图中,由于m1和A漂浮,根据漂浮条件可得ρ水gV=GA+m1g,求出m1的大小;在丁图中,由于m2和A漂浮,根据漂浮条件可得ρ液gV=GA+m2g,求出m2的大小;由题知m1:m2=5:1,据此求出另一种液体的密度;
(3)根据乙图中,木块漂浮时,浮力等于重力即可求出木块的密度。
【解答】解:(1)设A的体积为V、容器的底面积为S,
∵A在水中漂浮,
∴F浮=ρ水V排g=ρ水Vg=GA,
甲图和乙图比较,容器底受到的压力差:ΔF=GA,
比较甲、乙两图,ΔP====300Pa,﹣﹣﹣﹣①
同理,比较甲丙图,ΔP′===400Pa,﹣﹣﹣﹣②
得:
mA:m1=3:1,
V排′=V;
此时木块A露出水面的部分占自身体积;故A错误,D正确。
(2)在丙图中,由于m1和A漂浮,可得:
ρ水gV=GA+m1g=ρ水gV+m1g,
∴m1=ρ水V,
在丁图中,ρ液gV=GA+m2g=ρ水gV+m2g,
∴m2=ρ液V﹣ρ水V,
∵m1:m2=5:1,
即:
(ρ水V):(ρ液V﹣ρ水V)=5:1,
解得:
ρ液=0.8ρ水=0.8×1.0×103kg/m3=0.8×103kg/m3.故B正确;
(2)在乙图中,木块漂浮,则
ρ水gV=ρ木gV
ρ木=ρ水=×1×103kg/m3=0.6×103kg/m3.故C正确。
故选:A。
11.【分析】(1)知道均匀实心长方体木块A的边长和体积,根据V=Sh求出其体积,利用ρ=求出木块A的密度;
(2)当加入1.8kg的水时,木块A对容器底部的压力刚好为0,此时木块恰好漂浮,根据物体浮沉条件和阿基米德原理求出木块排开水的体积,根据V=Sh求出容器内水的深度,根据ρ=求出容器内加入水的体积,利用V水=(S容﹣SA)h水求出容器的底面积;
(3)细绳拉断前、后木块静止时,根据p=ρgh求出容器内水深度的变化量,根据ΔV排=S容Δh求出木块排开水体积的减少量,然后求出剪断细绳前木块排开水的体积,根据阿基米德原理求出木块受到的浮力,根据V=Sh求出细绳拉断前木块浸入水中的深度,进一步求出容器内水的深度和容器内水的体积,根据m=ρV求出最后容器中水的总质量。
【解答】解:
(1)木块的体积:
VA=SAhA=100cm2×12cm=1200cm3,
木块的密度:
ρA===0.75g/cm3=0.75×103kg/m3,故A错误;
(2)当加入1.8kg的水时,木块A对容器底部的压力刚好为0,此时木块恰好漂浮,
因木块受到的浮力和自身的重力相等,
所以,由阿基米德原理可得F浮=G木=ρ水gV排,即m木g=ρ水gV排,
则木块排开水的体积:
V排===900cm3,
容器内水的深度:
h水===9cm,
容器内加入水的体积:
V水===1800cm3,
由V水=(S容﹣SA)h水可得,容器的底面积:
S容=+SA=+100cm2=300cm2,故B错误;
(3)细绳拉断前、后木块静止时,由p=ρgh可得,容器内水深度的变化量:
Δh===5×10﹣3m=0.5cm,
木块排开水体积的减少量:
ΔV排=S容Δh=300cm2×0.5cm=150cm3,
则剪断细绳前木块排开水的体积:
V排′=V排+ΔV排=900cm3+150cm3=1050cm3,
木块受到的浮力:
F浮′=ρ水gV排′=1.0×103kg/m3×10N/kg×1050×10﹣6m3=10.5N,故C错误;
细绳拉断前木块浸入水中的深度:
h水′===10.5cm,
容器内水的深度:
h水″=h水′+h绳=10.5cm+8cm=18.5cm,
容器内水的体积:
V水总=S容h水″﹣V排′=300cm2×18.5cm﹣1050cm3=4500cm3,
则最后容器中水的总质量:
m水总=ρ水V水总=1.0g/cm3×4500cm3=4500g=4.5kg,故D正确。
故选:D。
12.【分析】根据F浮=ρ水gV物 求得物块浸没在水和酒精中受到的浮力;然后对物块浸没在水中和酒精中进行受力分析,然后根据二力平衡列出等式首先求出物块的重力;
(1)根据力的平衡和力的相互作用即可求出弹簧对物块的支持力和弹簧对底部的拉力;
(2)当弹簧脱离容器底部后静止时物块处于漂浮状态,根据漂浮条件即可求出浸没的体积与物块的体积之比,然后求出露出水面的体积与物块体积的关系;
(3)根据G=mg即可求出物块的质量。
【解答】解:物块的体积V物=100cm3=1×10﹣4m3,物块浸没在水和酒精中时V排=V物=1×10﹣4m3,
物块浸没在水中:F浮=ρ水gV物=1.0×103kg/m3×10N/kg×1×10﹣4m3=1N。
物块浸没在酒精中:F浮′=ρ酒精gV物=0.8×103kg/m3×10N/kg×1×10﹣4m3=0.8N。
物块浸没在水中和酒精中受力分析分别如图甲、乙所示;
若物块都受弹簧的支持力,由于重力不变,浮力不同,故这种情况不可能;同理都受弹簧的拉力也不可能。
只可能是一个为拉力,另一个为支持力。由于物块在水中浮力大,物块会上浮,故弹簧会对它有拉力;在酒精中物块会受支持力作用。
所以根据物体受力平衡可得:
图甲中:F浮=F拉+G,
所以,F拉=F浮﹣G=1N﹣G﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
图乙中:F浮′+F支=G,
所以,F支=G﹣F浮′=G﹣0.8N﹣﹣﹣﹣﹣﹣﹣﹣﹣②,
已知:当物块浸没在水中静止时与浸没在酒精中静止时,弹簧的弹力大小相等;
即:F拉=F支,
所以,1N﹣G=G﹣0.8N
解得:G=0.9N;
A、物块浸没在水中静止时,弹簧会对物块的拉力为F拉=F浮﹣G=1N﹣0.9N=0.1N,
由于力的作用是相互的,则弹簧对底部的拉力F拉′=F拉=0.1N,故A错误;
B、当弹簧脱离容器底部后静止时物块处于漂浮,则:F浮″=G=0.9N,
根据F浮=ρ液gV排可得:V排″===9×10﹣5m3,
所以,===;故B错误;
C、物块浸没在酒精中静止时弹簧对物块的支持力F支=G﹣F浮′=0.9N﹣0.8N=0.1N;故C正确;
D、质量m===0.09kg,故D错误。
故选:C。
13.【分析】(1)设A的体积为V、容器的底面积为S,由于容器为圆柱形容器,在水中放入木块A后,A在水中漂浮,容器底受到的压力的变化值等于木块A的重力;而木块受到的浮力等于木块的重力,则压强变化值ΔP====;同理,比较甲丙图,压强变化值ΔP′==,知道ΔP、ΔP′的大小,可求丙图排开水的体积大小,进而求出木块A的质量mA与m1之比和木块A露出水面的部分占自身体积比值;
(2)在丙图中,由于m1和A漂浮,根据漂浮条件可得ρ水g V=GA+m1g,求出m1的大小;在丁图中,由于m2和A漂浮,根据漂浮条件可得ρ液g V=GA+m2g,求出m2的大小;由题知m1:m2=5:1,据此求出另一种液体的密度;
(3)根据乙图中,木块漂浮时,浮力等于重力即可求出木块的密度。
【解答】解:(1)设A的体积为V、容器的底面积为S,
∵A在水中漂浮,
∴F浮=ρ水V排g=ρ水(1﹣)Vg=GA,
甲图和乙图比较,容器底受到的压力差:ΔF=GA=mAg,
比较甲、乙两图,Δp====300Pa﹣﹣﹣﹣①
同理,比较甲丙图,Δp′====400Pa﹣﹣﹣﹣②
由 得:mA:m1=3:1,V排′=V;
此时木块A露出水面的部分占自身体积 ;故AC错误。
(2)在丙图中,由于m1和A漂浮,可得:
ρ水g V=GA+m1g=ρ水g V+m1g,
所以m1=ρ水V,
在丁图中,ρ液g V=GA+m2g=ρ水g V+m2g,
所以m2=ρ液V﹣ρ水V,
因为m1:m2=5:1,
即:(ρ水V):(ρ液V﹣ρ水V)=5:1,
解得:ρ液=0.8ρ水=0.8×1.0×103kg/m3=0.8×103kg/m3=0.8g/cm3.故D正确;
(3)在乙图中,木块漂浮,则ρ水gV=ρ木gV,
所以ρ木=ρ水=×1×103kg/m3=0.6×103kg/m3.故B错误。
故选:D。
14.【分析】要解决此题,需要掌握二力平衡条件,知道处于平衡状态的物体受平衡力的作用,一对平衡力的大小相等。
B在水中,所以受到水对它的浮力作用,所以B对A的拉力为F=G﹣F浮。
需要对物体A进行受力分析,确定两种情况下所受摩擦力的方向。根据二力平衡的条件列出两种情况下的关系式便可解决。
【解答】解:当用铝块C时,物体A向左匀速运动,所以所受摩擦力方向水平向右。
物体B在水中,受水对它向上的浮力,所以B对A的拉力FB=GB﹣F浮。
根据二力平衡条件:GC=f+GB﹣F浮
B、C是体积相同的实心铝块,所以重力相等。因此f=F浮。
若换为D,物体A向右匀速运动,所以所受摩擦力方向水平向左。
根据二力平衡条件:GD+f=GB﹣F浮,则GD=GB﹣f﹣F浮 又因为f=F浮,
所以GD=GB﹣2F浮 即mDg=ρ铝VBg﹣2ρ水VBg
则mD=ρ铝VB﹣2ρ水VB=2.7g/cm3×10cm3﹣2×1g/cm3×10cm3=7g
故选:B。
15.【分析】冰熔化前,由于冰、木块、铁钉处于漂浮状态,根据漂浮条件和阿基米德原理求排开水的体积;
冰熔化后,冰变成水,因为水的质量、重力不变,可求水的体积;木块仍然漂浮,根据漂浮条件和阿基米德原理求排开水的体积;铁钉下沉,根据阿基米德原理求排开水的体积;
计算冰熔化前后排开水的体积关系,得出水面升降。
【解答】解:
冰熔化前,冰和木块处于漂浮状态,
F浮=G冰+G木+G铁,
即:ρ水gV排=G冰+G木+G铁,
∴V排=++,
冰熔化后,冰变成水,木块仍然漂浮,铁钉下沉,
冰熔化成水的体积为:
V水==,
木块排开的水的体积为:
V木排=,
铁钉排开水的体积:
V铁=,
此时排开水的体积:
V=V水+V木排+V铁=++,
∵铁钉下沉,
∴F浮铁钉<G铁,
∵V<V排,
∴水面下降。
故选:C。
16.【分析】(1)根据体积公式计算A杯浸入水中的体积,根据F浮=ρ水gV排计算A杯受到的浮力;
对A进行受力分析可知:A受到竖直向下的重力和弹簧对A的拉力,以及竖直向上的浮力,进一步计算弹簧对A的作用力;
(2)如图乙所示,向A杯中加水杯子对弹簧的拉力减小,随着水的增多,拉力逐渐变为压力,
当水槽液面恰好与A杯口相平时停止加水,弹簧对A杯的作用力大小与甲图中弹簧对A杯的作用力大小相等,据此可知A杯对弹簧的压力,
弹簧每受1N的拉力时,弹簧伸长0.5cm,据此计算计算两图中弹簧长度的变化,据此可知与甲图相比,乙图中A向下移动的距离,进一步计算乙图中弹簧的长度和甲图水槽内水面高度,
根据体积公式计算与甲图相比,乙图水面上升的高度;
(3)由②可知乙图中A杯浸入水中的深度,根据体积公式、F浮=ρ水gV排计算乙图中A杯受到的浮力;
A杯受弹簧的支持力为4N,A杯和杯里的水受力平衡,即G杯+G水=F浮乙+F乙,代入数据解方程可得水的重力,
与甲图相比乙图水槽对桌面压力的增加量等于加入杯中的水的重力,据此可知水槽对桌面的压力增加了多少;
根据重力公式、密度公式计算A杯里的水的体积,根据体积公式计算A杯里的水的高度,根据连通器原理可知乙图中打开阀门B,待水静止后,水槽里面的水面高度的变化,根据液体压强公式计算水对槽底的压强。
【解答】解:(1)A杯浸入水中的体积为:V排=SAhA=100cm2×8cm=800cm3=8×10﹣4m3,
则A杯受到的浮力为:F浮=ρ水gV排=1×103kg/m3×10N/kg×8×10﹣4m3=8N;
对A进行受力分析可知:A受到竖直向下的重力和弹簧对A的拉力,以及竖直向上的浮力,
由二力平衡关系可知弹簧对A的作用力为:F拉=F浮﹣GA=8N﹣4N=4N,方向竖直向下,故①正确;
(2)如图乙所示,向A杯中加水杯子对弹簧的拉力减小,随着水的增多,拉力逐渐变为压力,
当水槽液面恰好与A杯口相平时停止加水,弹簧对A杯的作用力大小与甲图中弹簧对A杯的作用力大小相等,所以此时弹簧对A杯的支持力大小为4N,即A杯对弹簧的压力为4N,
弹簧每受1N的拉力时,弹簧伸长0.5cm,此时弹簧被压缩了2cm,
甲图中弹簧对A杯竖直向下的拉力为4N,弹簧被拉长了2cm,与甲图相比,乙图中A向下移动的距离为4cm,
如图:
则乙图中弹簧的长度l′=l+2cm﹣4cm=10cm+2cm﹣4cm=8cm,
甲图水槽内水面高度h=l+2cm+h1=10cm+2cm+8cm=20cm,
A杯浸入水中的深度为8cm,向A杯加水时,水槽中的水体积不变,
与甲图相比,乙图水面上升Δh===2cm,故②错误;
(3)由②可知,乙图中A杯浸入水中的深度为h2=8cm+4cm+2cm=14cm,
乙图中A杯受到的压力为F浮乙=ρ水gV排乙=1×103kg/m3×10N/kg×(14×100)×10﹣6m3=14N;
A杯受弹簧的支持力为4N,A杯和杯里的水受力平衡,即G杯+G水=F浮乙+F乙,
代入数据可得4N+G水=14N+4N,解方程可得水的重力G水=14N,
与甲图相比乙图水槽对桌面压力的增加量等于加入杯中的水的重力,即水槽对桌面的压力增加了14N,故③错误;
杯里的水的体积:V水===0.0014m3=1400cm3,
杯里的水的高度hA===14cm,
则A杯内外水面相平,乙图中打开阀门B,此时水杯和水槽相当于连通器,待水静止后,水槽里面的水面高度不变,
水槽里面的水面高度:h′=h+Δh=20cm+2cm=22cm=0.22m,
水对槽底的压强为p=ρ水gh′=1.0×103kg/m3×10N/kg×0.22m=2200Pa,故④正确。
故选:C。
17.【分析】(1)设A的体积为V、容器的底面积为S,由于容器为圆柱形容器,在水中放入木块A后,A在水中漂浮,容器底受到的压力的变化值等于木块A的重力;而木块受到的浮力等于木块的重力,则压强变化值Δp===;同理,比较甲丙图,压强变化值Δp′==;比较甲丁图,压强变化值Δp″=;知道Δp、Δp′的大小,可求丙图排开水的体积大小,进而求出木块A的质量mA与m1之比、木块A露出水面的部分占自身体积比值和图丁与图甲比较,液体对容器底部的压强变化值;
(2)根据乙图中,木块漂浮时,浮力等于重力即可求出木块的密度。
【解答】解:设A的体积为V、容器的底面积为S,
A在水中漂浮,
所以F浮=ρ水V排g=ρ水Vg=GA,
甲图和乙图比较,容器底受到的压力差:ΔF=GA,
比较甲、乙两图,Δp====300Pa,﹣﹣﹣﹣①
同理,比较甲丙图,Δp′===400Pa,﹣﹣﹣﹣②
比较甲丁图,Δp″=﹣﹣﹣﹣③
得:
=,=,
解得mA:m1=3:1,
V排′=V;
此时木块A露出水面的部分占自身体积,即木块A露出水面的体积与木块A的体积之比是1:5,故A错误,C错误。
在乙图中,木块漂浮,则
ρ水gV=ρ木gV
ρ木=ρ水=×1×103kg/m3=0.6×103kg/m3.故B正确。
②﹣①得:=100Pa,则G1=100Pa×S﹣﹣﹣﹣﹣﹣﹣④,
已知m1:m2=5:1,则G2=G1=×100Pa×S=20Pa×S﹣﹣﹣﹣﹣⑤,
由①可得,GA=300Pa×S﹣﹣﹣﹣﹣﹣⑥,
丙丁两图中物体都漂浮,且由题意可知,A排开水的体积相同,则:
G1+GA=ρ水gV排﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑦
G2+GA=ρ液gV排﹣﹣﹣﹣﹣﹣﹣﹣﹣⑧
将④⑤⑥代入⑦⑧解得:ρ液=0.8ρ水,
因丙丁两图中水和液体的体积相同,则G液=0.8G水,
图丁中液体对容器底部的压强:
p丁===320Pa+,
图甲中水对容器底部的压强:
p甲=,
所以,图丁与图甲比较,液体对容器底部的压强增加量:
Δp″=p丁﹣p甲=320Pa+﹣=320Pa﹣,故D错误。
故选:B。
18.【分析】(1)由图乙可知,压力传感器的示数先减小,到15min时突然增大到200N不变,说明绳子无拉力,此时F=GB;
(2)由图甲可计算水和圆柱体的总体积V=S容器h总,由抽水速度和抽水时间可知V水,即可求得VA,再由阿基米德原理求A浸没时受到的浮力;根据A受力平衡可求A的重力,根据G=mg求出A的质量,利用ρ=求出A的密度;
(3)由VA及h0,可求SA;由图乙可知,t=15min时绳子拉断,根据抽水速度求出此时容器里的水面下降的高度,据此可知A浸入水的深度,即可求得A排开水的体积VA排,由阿基米德原理求A浸没时受到的浮力;根据A受力平衡可求绳子的拉力和压力传感器的示数;
(4)利用图象,结合A、B的受力确定A浸没时所受浮力的最大值和最小值,再由阿基米德原理求液体的密度。
【解答】解:A、由图乙可知,随水位下降,压力传感器示数应不断减小,在A脱离液面时达到稳定,而图乙中15min时示数突然增大,可推断此时绳子突然断开(达到了绳子的最大承受力),故15min后压力传感器的示数等于B所受的重力,即GB=F=200N,故A错误;
B、由图甲可知,水和圆柱体的总体积:
V=S容(h0+h1)=400cm2×(40cm+20cm)=400cm2×60cm=24000cm3,
由于以400cm3/min的速度将水抽出,40min恰能将水全部抽出,则水的体积为:
V水=400cm3/min×40min=16000cm3,
则圆柱体A的体积:
VA=V﹣V水=24000cm3﹣16000cm3=8000cm3=8×10﹣3m3,
因为物体A不吸水,浸没时排开水的体积等于自身体积,即
V排=VA=8×10﹣3m3,
依据阿基米德原理可得,A浸没时所受的浮力:
F浮1=ρ水gV排=1.0×103kg/m3×10N/kg×8×10﹣3m3=80N;
由图乙可知,分析B的受力,当压力传感器示数F1=120N时,绳子的拉力:
F拉1=GB﹣F1=200N﹣120N=80N,
分析A的受力,受重力GA、绳子的拉力F拉1和水的浮力F浮1,则有GA=F拉1+F浮1=80N+80N=160N,
物体A的质量:mA===16kg,
物体A的密度为ρA===2×103kg/m3,故B错误;
C、由VA=8000cm3,h0=40cm可得圆柱体的底面积
SA===200cm2;
由图乙可知,t=15min时绳子拉断,则此时抽出的水的体积为:
V水′=400cm3/min×15min=6000cm3,
则水面下降的高度为:Δh===30cm,
此时圆柱体A浸入水的深度:h浸=h0﹣Δh=40cm﹣30cm=10cm,
此时A物体排开液体的体积为V排′=SAh浸=200cm2×10cm=2000cm3=2×10﹣3m3,
A物体所受浮力:F浮2=ρ水gV排′=1.0×103kg/m3×10N/kg×2×10﹣3m3=20N;
根据受力平衡可知:F拉2=GA﹣F浮2=160N﹣20N=140N,
压力传感器的示数F2=GB﹣F拉2=200N﹣140N=60N,故C正确;
D、因绳子的最大拉力Fmax=F拉2=140N,
由于A的重力为GA=160N,则A所受浮力最小为:F浮小=GA﹣F拉max=160N﹣140N=20N,
且A浸没在液体中时V排=VA=8×10﹣3m3,
则液体的最小密度为ρ最小===0.25×103kg/m3;
A浸没时所受的最大浮力与A的重力相等,即F浮大=GA=160N,则可测量的液体密度最大为:
ρ最大===2×103kg/m3,
所以该密度测量仪的测量范围是0.25×103kg/m3~2×103kg/m3,故D错误。
故选:C。
19.【分析】(1)根据题意可知弹簧上方连有正方体木块A时弹簧的压缩量,利用“弹簧的长度每改变1cm,所受力的变化量为1N”求出弹簧产生的弹力,物体A静止时受到的重力与弹簧产生的弹力是一对平衡力,据此求出物体A的重力;
(2)根据V=L3求出木块的体积,当木块A有的体积浸入液体中时,弹簧恰好处于自然伸长状态,则木块处于漂浮状态受到的浮力和自身的重力相等,根据F浮=ρgV排求出液体的密度;
(3)先求出木块A有的体积浸入液体中时液体的深度,根据体积公式求出此时容器内液体的体积,在木块A正上方放置一合金块B,静止时液面刚好浸没B,利用V=Sh求出此时液体的深度,利用p=ρgh求出放置合金块B后液体对容器底部的压强;
(4)在木块A正上方放置一合金块B,静止时液面刚好浸没B时,先求出弹簧的长度,然后求出弹簧的压缩量,进一步求出此时弹簧产生的向上弹力,根据F浮=ρgV排求出A、B受到的总浮力,以A、B整体为研究对象,整体受到竖直向下A和B的重力、竖直向上整体浮力和向上的弹力处于平衡状态,利用A、B整体受到的合力为零求出B的重力。
【解答】解:(1)由题意可知,弹簧上方连有正方体木块A时,其长度只有L1=6cm,则弹簧的压缩量Δx=L0﹣L1=10cm﹣6cm=4cm,
因弹簧的长度每改变1cm,所受力的变化量为1N,所以,弹簧产生的弹力F=4cm×1N/cm=4N,
因物体A静止时,受到的重力与弹簧产生的弹力是一对平衡力,所以,物体A的重力GA=F=4N,故A正确;
(2)木块的体积:VA==(10cm)3=1000cm3=1×10﹣3m3,
当木块A有的体积浸入液体中时,弹簧恰好处于自然伸长状态,则木块处于漂浮状态,木块受到的浮力F浮=G=4N,
由F浮=ρgV排可得,液体的密度:ρ液===0.8×103kg/m3,故B正确;
(3)当木块A有的体积浸入液体中时,液体的深度:h=L0+h浸=10cm+×10cm=15cm,
此时容器内液体的体积:V液=S容h﹣VA=200cm2×15cm﹣×1000cm3=2500cm3,
在木块A正上方放置一合金块B,静止时液面刚好浸没B,
则此时液体的深度:h′===18cm=0.18m,
则放置合金块B后液体对容器底部的压强:p=ρ液gh′=0.8×103kg/m3×10N/kg×0.18m=1440Pa,故C正确;
(4)在木块A正上方放置一合金块B,静止时液面刚好浸没B时,弹簧的长度L2=h′﹣LA﹣hB=18cm﹣10cm﹣4cm=4cm,
则弹簧的压缩量Δx′=L0﹣L2=10cm﹣4cm=6cm,
此时弹簧产生的向上弹力:F′=6cm×1N/cm=6N,
A、B受到的总浮力:F浮总=ρ液g(VA+VB)=0.8×103kg/m3×10N/kg×(1×10﹣3m3+100×10﹣6m3)=8.8N,
以A、B整体为研究对象,整体受到竖直向下A和B的重力、竖直向上整体浮力和向上的弹力处于平衡状态,
由A、B整体受到的合力为零可得:F浮总+F弹=GA+GB,
则B的重力:GB=F浮总+F弹﹣GA=8.8N+6N﹣4N=10.8N,故D错误。
故选:D。
20.【分析】(1)已知塑料块的边长,求出塑料块的体积;塑料块下方刚好与水面接触时,测力计测量塑料块的重力,根据G=mg求出塑料块的质量,利用ρ=即可求出塑料块的密度;
(2)当加入1000cm3水时,塑料块会上浮,由于塑料块受到的浮力等于测力计的示数变化,根据塑料块升高的高度,得出弹簧伸长量的变化,然后即可求出浮力;根据阿基米德原理求出塑料块浸入水中的体积(排开水的体积),则即可求出物体浸没的深度,
则两种情况下的高度之和就是水面变化的高度,根据底面积求出加入水的体积,由于加入水的体积已知,据此即可求出塑料块会上浮的高度hm,继而求出浮力。
(3)同上求出当加入3000cm3水时,塑料块会上浮的高度h′m,然后根据水的体积变化求出水的深度,利用p=ρgh求容器底部所受压强;
(4)当加水至塑料块刚好漂浮时说明塑料块受到浮力F浮″=G,根据F浮=ρgV排得塑料块漂浮时浸入水中的体积,然后求出浸入的深度,
由于物体向上移动时,塑料块底面以上周围的水会补充到塑料块下面,当向外排水后,弹簧测力计示数再次回到5N,即塑料块下方刚好与水面再次接触,
此时塑料块移动后塑料块下面的水的体积与排出的水的体积等于塑料块周围水的体积;据此即可求出需要移动的时间。
【解答】解:A、塑料块的体积V=L3=(10cm)3=1000cm3;
当塑料块底面刚好接触水面时。弹簧测力计示数为5N,即G=5N;
则塑料块的质量m===0.5kg=500g,
塑料块的密度ρ===0.5g/cm3;故A错误;
B、设当加入1000cm3水时,塑料块上浮hm,则弹簧的伸长将减小hm,
由于弹簧受到1N的拉力时伸长1cm,则弹簧的拉力减小量为ΔF1=100hN,
此时塑料块受到浮力F浮=ΔF1=100hN。
由F浮=ρgV排得此时塑料块浸入水中的体积:
V排==;
S塑料=L2=(10cm)2=100cm2=100×10﹣4m2,
则塑料块浸入水的深度为h浸==,
所以,S容器h+(S容器﹣S塑料)h浸=V加水,
即:S容器h+(S容器﹣S塑料)=V加水,
所以,300×10﹣4m2×hm+(300×10﹣4m2﹣100×10﹣4m2)×=1000×10﹣6m3,
解得:h=0.02,
所以当加入1000cm3水时,塑料块上浮0.02m,塑料块受到浮力:
F浮′=ΔF1=100hN=100×0.02N=2N;故B错误;
C、当所加的水使物块漂浮时,此时物块受到的浮力F浮=G=5N,
则V排===5×10﹣4m3=500cm3,
此时物块浸入水中的深度h浸===5cm,
最初的拉力为5N,则加水使物块漂浮时,拉力减小了5N,由题意可知弹簧会缩短5cm,即物块会向上移动5cm,
所以此时水的深度H=h0+h向上+h浸=5cm+5cm+5cm=15cm,
此时水对容器底的压强p=ρ水gh水=1.0×103kg/m3×10N/kg×0.15m=1500Pa,
所加水的体积:V加=S容器H﹣V排﹣S容器h0=300cm2×15cm﹣500cm3﹣300cm2×5cm=2500cm3,故C错误;
D、当加水至塑料块刚好漂浮时,则测力计的示数为零,所以,塑料块受到浮力F浮″=G=5N,
由F浮=ρgV排得塑料块浸入水中的体积:
V排″===5×10﹣4m3=500cm3;
则塑料块浸入水的深度为:h浸″===5cm,
此时塑料块底面以上的水的体积V′=(S容器﹣S塑料)h浸″=(300cm2﹣100cm2)×5cm=1000cm3,
当物体向上移动时,塑料块底面以上周围的水会补充到塑料块下面,则塑料块移动后下面的水的体积与排出的水的体积等于塑料块周围水的体积;
物体向上移动的高度为h物=v物t=1cm/s×t,
则塑料块上移后下面的水的体积:V下=S容器h物=S容器v物t=300cm2×1cm/s×t,
排出的水的体积V排出=v排t=50cm3/s×t,
所以,V下+V排出=V′,
即:300cm2×1cm/s×t+50cm3/s×t=1000cm3,
解得:t≈2.86s,故D正确。
故选:D。
二.填空题(共10小题)
21.【分析】整体分析甲,由题知,物体漂浮,有 的体积露出水面,利用阿基米德原理求出受到的浮力;
整体分析乙,因为在乙容器中,A、B通过细绳相连,所以物体A、B的重力等于其在液体中受到的浮力加上B受到容器底的支持力为F支;
隔离法分析乙,A物体的重力加上细绳的拉力等于它在此液体中受到的浮力;B物体的重力等于细绳的拉力加上它在此液体中受到的浮力,再加上B受到容器底的支持力;根据以上分析,列出算式,将已知条件代入及可求得结论。
【解答】解:
由题知,物体漂浮,有 的体积露出水面,此时浮力等于二者重力,则F浮=GA+GB=ρ1gVA﹣﹣﹣﹣﹣①
在乙容器中,A、B通过细绳相连,物体A、B的重力等于其在液体中受到的浮力加上B受到容器底的支持力为F支,即GA+GB=ρ2g(VA+VB)+F支﹣﹣﹣﹣②
单独对乙容器中的A物体进行受力分析,A物体受到的浮力等于A物体的重力加上细绳的拉力,即GA+F拉=ρ2gVA﹣﹣﹣﹣﹣③
B物体的重力等于细绳的拉力加上它在此液体中受到的浮力,再加上B受到容器底的支持力,即GB=F拉+ρ2gVB+F支﹣﹣﹣﹣﹣④
联立①②可得:F支=ρ1g×VA﹣ρ2g(VA+VB)﹣﹣﹣﹣﹣﹣﹣⑤
已知F支:F拉=1:3,即F拉=3F支﹣﹣﹣﹣﹣﹣﹣⑥
由③⑤⑥可得:mA=4ρ2VA﹣ρ1VA+3ρ2VB
由④⑤⑥可得:mB=3ρ1VA﹣4ρ2VA﹣3ρ2VB
已知ρ1:ρ2=2:1,VA:VB=4:1,
则ρA==4ρ2﹣ρ1+3ρ2=4ρ2﹣ρ1+3ρ2×=ρ2;
ρB==3ρ1×﹣4ρ2×﹣3ρ2=5ρ2;
故ρA:ρB=ρ2:5ρ2=1:20。
故答案为:1:20。
22.【分析】(1)已知冲锋舟满载时排开水的体积,根据公式F浮=ρgV排可求冲锋舟满载时所受的浮力;
(2)冲锋舟满载漂浮时所受的浮力等于自身的重力与人的重力之和;冲锋舟最多承载人的重力与自重的和等于满载时的浮力,从而求出最多超载的人数;
(3)已知冲锋舟底部所处的深度,根据公式P=ρgh可求所受的压强。
【解答】解:(1)冲锋舟满载时所受的浮力是F浮=ρgV排=1000kg/m3×10N/kg×1.5m3=1.5×104N;
(2)一个人的重力G=mg=60kg×10N/kg=600N;
最多承载的人数为n===15人;
(3)冲锋舟底部0.5m深处所受水的压强P=ρgh=1000kg/m3×10N/kg×0.5m=5×103Pa;
故答案为:1.5×104;15;5×103。
23.【分析】(1)根据物块m物1在试管内漂浮F浮1=G物1,求出Δh0表示试管中液体上升的高度的表达式;根据试管中放入物块使得试管整体受到的浮力的增加量ΔF浮1=G物1,即ρ水gΔh1S1=ρ水gS2Δh2求出试管底部浸入容器中水的深度的增加量Δh1、放置物块试管下沉容器液面上升的高度Δh2的表达式,结合放入物块后试管内水面与容器底部的距离h′与原h的关系h′=h﹣(Δh1﹣Δh2)+Δh0,与h比较大小做出判断;
(2)已知S2=nS1,试管始终漂浮,受到的浮力的增加量等于物块的重力ΔF浮1=G物1,即ρ水gΔH1S1=ρ水g(S2﹣S1)ΔH2求出ΔH2与ΔH1的关系;由题意知将另一物块完全浸没在该试管水中,发现试管内水面与容器底部的距离恰好又变为h,可知ΔH1﹣ΔH2=ΔH0,求出ΔH0与ΔH1的关系;进一步又因为试管仍然漂浮,所以新排开的水重等于新加入的物体重G物2=ΔF浮2=ρ水gΔV2,则m物2g=ρ物2 V物2=ρ水gΔV2,结合V排2=V物2=S1ΔH0、ΔV2=S1ΔH1以及物块的密度以及求解新物块的密度;
(3)若外容器装的是盐水,内试管装的是纯水,同理(2)进行分析。
【解答】解:
(1)设Sl表示试管底面积,S2表示容器底面积,当物块漂浮在试管内的水面上时,因物块m物1在试管内漂浮F浮1=G物1,物块1排开试管中水的体积V排1=Δh0S1,则有:ρ水gV排1=ρ水gΔh0S1=m物1g;
其中Δh0=,Δh0表示试管中液体上升的高度;
因放入物块1使得试管排开的容器中水的体积的增加量为:
ΔV1=S1Δh1=S2Δh2,
其中Δh1表示试管底部浸入容器中水的深度的增加量,Δh2表示容器中液面上升的高度,
因放入物块1使得试管受到的浮力的增加量ΔF浮1=G物1,
即ρ水gΔV1=ρ水gΔh1S1=ρ水gS2Δh2=m物1g,
故可解得:
Δh1=;
Δh2=;
则此时试管内水面与容器底部的距离为:
h′=h﹣(Δh1﹣Δh2)+Δh0=h﹣[﹣]+=h+>h;
(2)当放置另一物块2完全浸没在该试管时,物块2排开试管中水的体积,V排2=V物2=S1ΔH0,其中ΔH0表示试管中液体上升的高度;
因放置物块2后试管下沉,试管排开容器中水的体积的增加量:
ΔV2=S2ΔH1=S1ΔH浸=S1(ΔH1+d)
其中ΔH1表示因放置物块试管下沉使得容器液面上升的高度,ΔH浸表示试管底部浸入容器中水的深度的增加量,d为试管向下移动的距离;
又S2=nS1,可得d=(n﹣1)ΔH1;
由试管内水面与容器底部的距离恰好又变为h可知:ΔH0=d=(n﹣1)ΔH1;
因为试管仍然漂浮,所以新排开的水重等于新加入的物体重,ΔF浮2=G物2,即ρ水gΔV2=m物2g=ρ物2gV物2,结合ΔV2=S2ΔH1以及V排2=V物2=S1ΔH0,则物块的密度:
ρ物2=ρ水=ρ水=ρ水=ρ水;
(3)若外容器装的是盐水,内试管装的是纯水,放入另一物块3仍满足液面高度h不变,则以上结论依然成立,同理可得:ρ物3=ρ盐水。
故答案为:>;ρ水;ρ盐水。
24.【分析】(1)因为密度计是一根两端封闭即空心的,所以能使密度计浮在液体表面,为了使它保持竖直的漂浮,就在管的底部封存少许铅粒;
(2)密度计的质量一定,在液体中受力平衡,受到的浮力总是等于重力,被测液体的密度越大,排开液体的体积越小,浸入液体部分也越小,据此分析回答;
(3)根据密度计的刻度由上至下数值逐渐增大分析;
(4)为了使测量结果更准确,使密度计上两条刻度线(如0.9、1.0)之间的距离大一些,因为ΔV=sh,所以可知减小S,即可使h变大,据此设计即可。
【解答】解:
(1)为了让饮料吸管能竖直的漂浮在液体中,吸管下端塞入一些铜丝作为配重,这样做目的是让密度计竖直漂浮在液体中;若将它放入液体中后不能竖直漂浮,则可以用小钢珠作为配重;
(2)密度计是漂浮在液体中,所受浮力等于本身的重力,保持不变,如果液体的密度越大,则密度计浸入液体中的体积越小,即越往上浮,则露出液面部分的长度越长;所以密度计的刻度是越往下值越大;
(3)因为密度计是漂浮在液体中,所受浮力等于本身的重力,则F浮水=F浮液=G,即ρ水gSH水=ρ液gSh液=G,
∵h液=H水,h液和ρ液是反比例函数;
∴刻度分布不均匀。且密度计的刻度由上至下数值逐渐增大;当密度的变化大时h液越变化越小,故C正确;
(4)因为ΔV=sh,所以使h变大,应减小S即可,具体做法是:用更细的吸管。
故答案为:(1)下端;可以用小钢珠作为配重(重心比铜丝低的材料都可以);
(2)越长;不变;
(3)C;
(4)用更细的吸管;
25.【分析】浸没在液体中的固体受到的浮力等于固体各表面所受液体压力的合力;我们可以先设想半球体下表面有液体,求出此时下表面受到的液体压力和半球体受到的浮力,从而求出此时液体对半球体上表面的压力;然后对半球体进行受力分析,求出把半球体从水中拉起需要的拉力。
【解答】解:(1)假设半球下表面处全部为液体,
则半球受到的浮力F浮方向竖直向上,由阿基米德原理可知,
F浮=ρgV排=ρgV半球=ρg××πr3=ρgπr3;
半球表面各处所受液体压力的分布如图所示,
半球上表面受到的液体压力F上竖直向下,
由p=可得,半球下表面受到的液体压力:
F下=p下S圆=p液S圆=ρgH×πr2,方向竖直向上,
半球受到的浮力F浮等于半球下表面与上表面所受液体对它的压力的合力,
即:F浮=F下﹣F上,F上=F下﹣F浮=ρgH×πr2﹣ρgπr3,
在本题给出的条件中,半球底部与容器底部紧密接触,即半球的下表面处并不与液体接触,
但这并不改变半球上表面受液体压力作用的情况,
则液体本身对半球的压力为F上=πr2ρgH﹣ρgπr3,
本题中要考虑大气压,大气压作用在液体上,且液体能传递压强,
则实际上液体对半球的压力为F上′=πr2ρgH﹣ρgπr3+p0πr2;
(2)半球刚要被拉起时,容器底板对半球的下表面已无向上的支持力,
则竖直向上的拉力F拉至少要等于上述的F上、半球本身的重力、大气压力之和,
即:F拉=F上+mg+p0S=πr2ρgH﹣ρgπr3+mg+p0πr2。
故答案为:πr2ρgH﹣ρgπr3+p0πr2;πr2ρgH﹣ρgπr3+mg+p0πr2。
26.【分析】(1)分析图示情景,找出浮力与物体排开液体体积的关系,然后得出结论。
(2)根据图示情景,求出浮力与物体排开液体重力的关系,然后得出结论。
(3)首先利用称重法求出乙物体受的浮力,再根据F浮=ρ水gV排求出乙物体的体积V=V排,再根据公式G=mg求出乙物体的质量,最后根据公式ρ=求出乙物体的密度。
【解答】解:(1)由图中(a)、(b)和(c)的实验可知:物体进入同种液体时,物体排开水的体积越大,物体受到的浮力越大。
(2)由图(d)和(e)所示实验可知:乙物体受的浮力F乙=G﹣F拉=5N
同课章节目录
- 第1章 水和水的溶液
- 第1节 地球上的水
- 第2节 水的组成
- 第3节 水的浮力
- 第4节 物质在水中的分散状况
- 第5节 物质的溶解
- 第6节 物质的分离
- 第7节 水资源的利用、开发和保护
- 第2章 天气与气候
- 第1节 大气层
- 第2节 气温
- 第3节 大气的压强
- 第4节 风和降水
- 第5节 天气预报
- 第6节 气候和影响气候的因素
- 第7节 我国的气候特征与主要气象灾害
- 第3章 生命活动的调节
- 第1节 植物生命活动的调节
- 第2节 人体的激素调节
- 第3节 神经调节
- 第4节 动物的行为
- 第5节 体温的控制
- 第4章 电路探秘
- 第1节 电荷与电流
- 第2节 电流的测量
- 第3节 物质的导电性与电阻
- 第4节 变阻器
- 第5节 电压的测量
- 第6节 电流与电压、电阻的关系
- 第7节 电路分析与应用
- 研究性学习课题
- 一 测定本地区的“酸雨”情况及分析原因
- 二 太阳黑子活动与本地区降水的关系
- 三 训练小动物建立某种条件反射
- 四 调查在自然界或生命活动中的电现象
