华师大版八年级上册课件:13.2.5三角形全等的判定(边边边)(共15张PPT)
文档属性
| 名称 | 华师大版八年级上册课件:13.2.5三角形全等的判定(边边边)(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 158.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-28 00:00:00 | ||
图片预览




文档简介
课件15张PPT。 三角形全等的判定
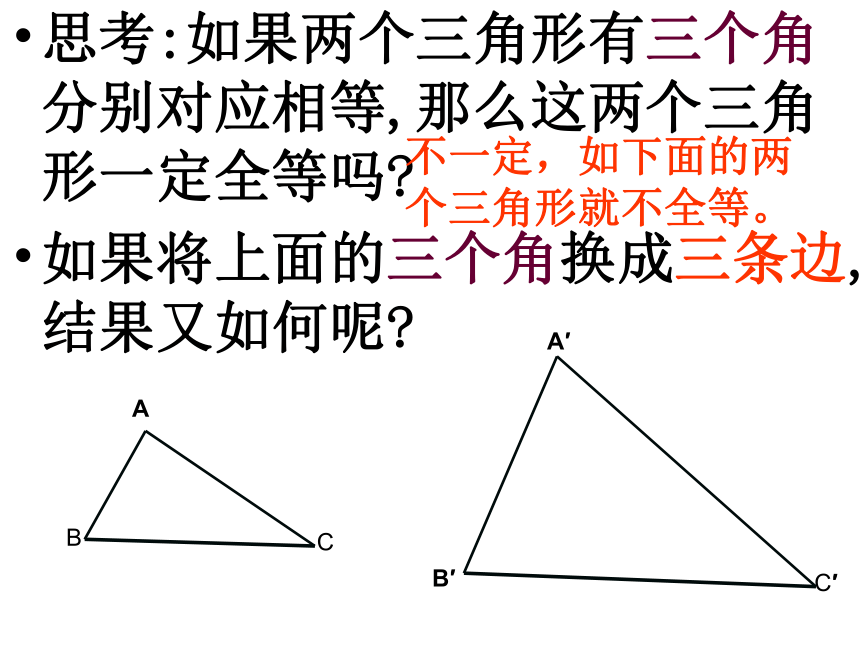
(S.S.S.)思考:如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?
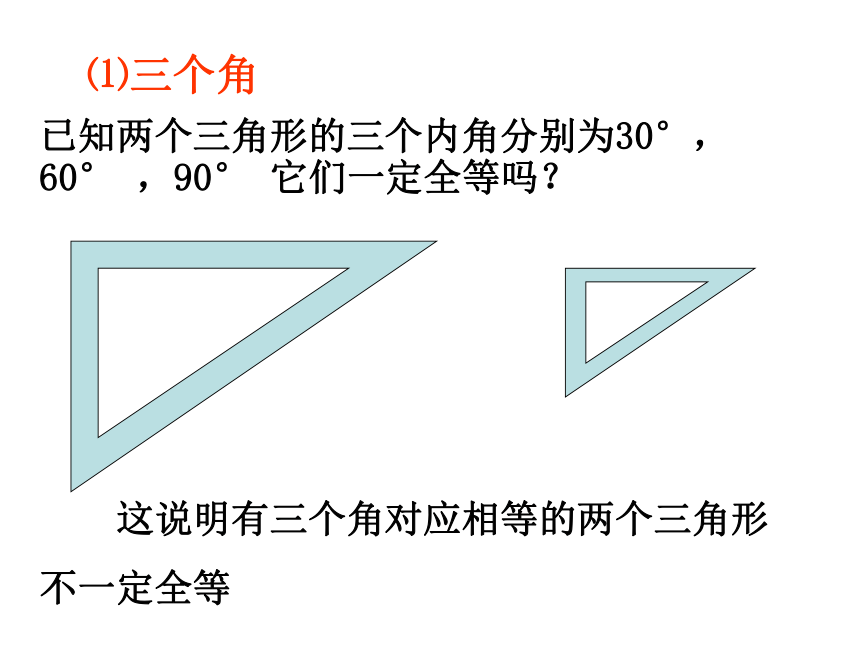
如果将上面的三个角换成三条边,结果又如何呢?不一定,如下面的两个三角形就不全等。已知两个三角形的三个内角分别为30°,60° ,90° 它们一定全等吗? 这说明有三个角对应相等的两个三角形
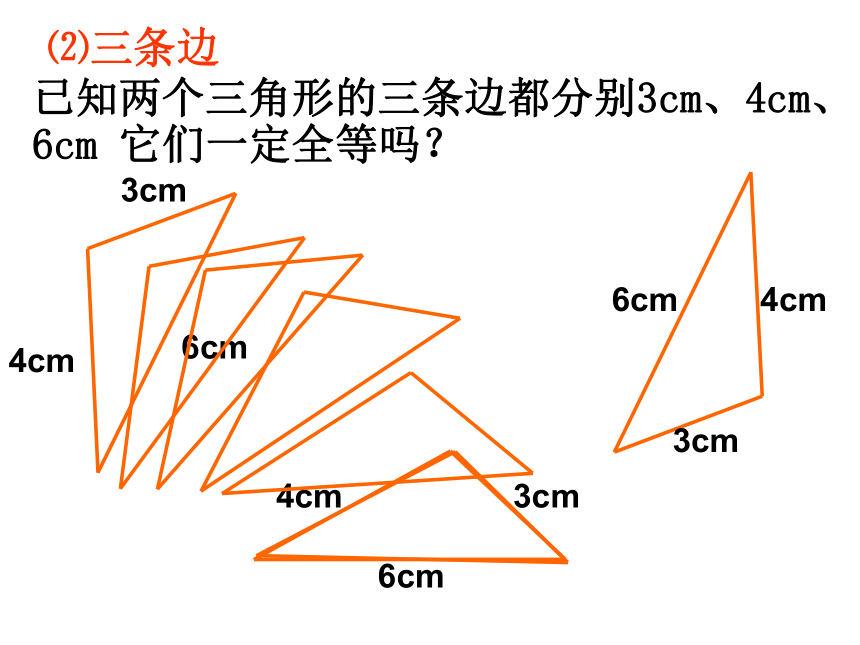
不一定全等⑴三个角已知两个三角形的三条边都分别3cm、4cm、6cm 它们一定全等吗?⑵三条边先任意画出一个△ABC,再画出一个△A’B’C’ ,使
A’B’= AB ,B’C’ =BC, A’ C’ =AC.把画好△A’B’C’的剪下,放到△ABC上,他们全等吗?画法:
1.画线段 B’C’ =BC;2.分别以 B’ , C’为圆心,BA,BC为半径画弧,两
弧交于点A’;3.连接线段 A’B’ , A’C’ .探究二上述结论反映了什么规律? 三边对应相等的两个三角形全等。
简写为“边边边”或“SSS”判定(4)边边边公理: 注: 这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有稳定性的原理。 如何用符号语言来表达呢?在△ABC与△DEF中ABCDEFAB=DE
AC=DF
BC=EF∴△ABC≌△DEF(SSS)判断两个三角形全等的推理过程,叫做证明三角形全等。例3:如图19.2.15,在四边形ABCD中,AD=BC, AB=CD.
求证:△ABC≌△CDA.
学以致用已知:如图,AB = DC , AD = BC。
求证: ∠A = ∠C练习提升提示:连结BC后,证△ABD≌△CDB,再根据全等三角形对应角相等推出∠A = ∠C。
一定
(S.A.S)不一定一定
(A.S.A)一定
(A.A.S)不一定一定
(S.S.S)
归纳:两个三角形全等的判定方法判定三角形全等至少有一组边练习:
1. 根据条件分别判定下面的三角形是否全等.
(1) 线段AD与BC相交于点O,AO=DO, BO=CO. △ABO与△BCO;
(2) AC=AD, BC=BD. △ABC与△ABD;
(3) ∠A=∠C, ∠B=∠D. △ABO与△CDO;
(4) 线段AD与BC相交于点E,AE=BE, CE=DE, AC=BD. △ABC与△BAD?全等(SAS)全等(SSS)不能判定全等。全等(SSS等)1、已知:如图.AB = DC , AC = DB
求证: ∠A = ∠D巩固提高练习提示:BC为公共边,由SSS可得两三角形全等,全等三角形对应角相等。4、已知:如图.AB = DC , AC = DB,
OA = OD
求证:∠A = ∠D
证明:∵AC=BD,OA=OD,
∴BD-OD=AC-OA,即
OB=OC.
∵AB=DC,OA=OD,
∴⊿OAB≌⊿ODC(SSS)
∴ ∠A = ∠D(全等三角形对应角相等)2.两个三角形全等的注意点:1.说明两三角形全等所需的条件应按
对应边的顺序书写.
2.结论中所出现的边必须在所证明的
两个三角形中. 小结3. 有时需添辅助线(如:造公共边)1.请说出目前判定三角形全等的4种方法:SAS,ASA,AAS,SSS
(S.S.S.)思考:如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?
如果将上面的三个角换成三条边,结果又如何呢?不一定,如下面的两个三角形就不全等。已知两个三角形的三个内角分别为30°,60° ,90° 它们一定全等吗? 这说明有三个角对应相等的两个三角形
不一定全等⑴三个角已知两个三角形的三条边都分别3cm、4cm、6cm 它们一定全等吗?⑵三条边先任意画出一个△ABC,再画出一个△A’B’C’ ,使
A’B’= AB ,B’C’ =BC, A’ C’ =AC.把画好△A’B’C’的剪下,放到△ABC上,他们全等吗?画法:
1.画线段 B’C’ =BC;2.分别以 B’ , C’为圆心,BA,BC为半径画弧,两
弧交于点A’;3.连接线段 A’B’ , A’C’ .探究二上述结论反映了什么规律? 三边对应相等的两个三角形全等。
简写为“边边边”或“SSS”判定(4)边边边公理: 注: 这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有稳定性的原理。 如何用符号语言来表达呢?在△ABC与△DEF中ABCDEFAB=DE
AC=DF
BC=EF∴△ABC≌△DEF(SSS)判断两个三角形全等的推理过程,叫做证明三角形全等。例3:如图19.2.15,在四边形ABCD中,AD=BC, AB=CD.
求证:△ABC≌△CDA.
学以致用已知:如图,AB = DC , AD = BC。
求证: ∠A = ∠C练习提升提示:连结BC后,证△ABD≌△CDB,再根据全等三角形对应角相等推出∠A = ∠C。
一定
(S.A.S)不一定一定
(A.S.A)一定
(A.A.S)不一定一定
(S.S.S)
归纳:两个三角形全等的判定方法判定三角形全等至少有一组边练习:
1. 根据条件分别判定下面的三角形是否全等.
(1) 线段AD与BC相交于点O,AO=DO, BO=CO. △ABO与△BCO;
(2) AC=AD, BC=BD. △ABC与△ABD;
(3) ∠A=∠C, ∠B=∠D. △ABO与△CDO;
(4) 线段AD与BC相交于点E,AE=BE, CE=DE, AC=BD. △ABC与△BAD?全等(SAS)全等(SSS)不能判定全等。全等(SSS等)1、已知:如图.AB = DC , AC = DB
求证: ∠A = ∠D巩固提高练习提示:BC为公共边,由SSS可得两三角形全等,全等三角形对应角相等。4、已知:如图.AB = DC , AC = DB,
OA = OD
求证:∠A = ∠D
证明:∵AC=BD,OA=OD,
∴BD-OD=AC-OA,即
OB=OC.
∵AB=DC,OA=OD,
∴⊿OAB≌⊿ODC(SSS)
∴ ∠A = ∠D(全等三角形对应角相等)2.两个三角形全等的注意点:1.说明两三角形全等所需的条件应按
对应边的顺序书写.
2.结论中所出现的边必须在所证明的
两个三角形中. 小结3. 有时需添辅助线(如:造公共边)1.请说出目前判定三角形全等的4种方法:SAS,ASA,AAS,SSS
