7.5正态分布 课件(共32张PPT)-2024-2025学年高二下学期数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 7.5正态分布 课件(共32张PPT)-2024-2025学年高二下学期数学人教A版(2019)选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-15 19:38:08 | ||
图片预览





文档简介
(共32张PPT)
高斯是一个伟大的数学家,一生中的重要贡献不胜枚举.德国的
10马克纸币上印有高斯的头像和正态分布的曲线,这就传达了一个信 息:在高斯的科学贡献中,对人类文明影响最大的是正态分布.
那么,什么是正态分布
正态分布的曲线有什么
特征
新课导入
学业标准
学科素养
1.通过误差模型,了解正态曲线、正态
分布的概念(重点). 2.通过借助具体实例的频率分布直方图, 了解正态分布的特征及曲线表示的含义 (重点).
1.通过正态分布相关概念的学习, 培养数学抽象等核心素养;
2.通过运用正态曲线的性质求随
3.了解正态分布的均值、方差及其含义 (难点).
机变量在某一区间的概率,提升数
学运算、直观想象等核心素养.
4.会用正态分布解决实际问题
学习目标
X 0 1 k
n
P
X 0 1 k
n
P
X 0
1
P
2、二项分布:X~B(n,p):
3、超几何分布:
复习旧知
1、两点分布:
生活中还有许多随机变量不是离散型的随机变量,例如:
①小明上学途中等公交车的时间X;
②实验中测量某零件尺寸的误差Y;
③秦皇岛5月份的降雨量Z;
④某电器的使用寿命;
●●
你还能举出几个这样的例子吗
连续型随机变量:
如果随机变量X的所有取值不可以逐个列举出来,而是充满某个 区间甚至整个实轴,但取一点的概率为0,我们称这类变量为连续型随 机变量。
情境导学
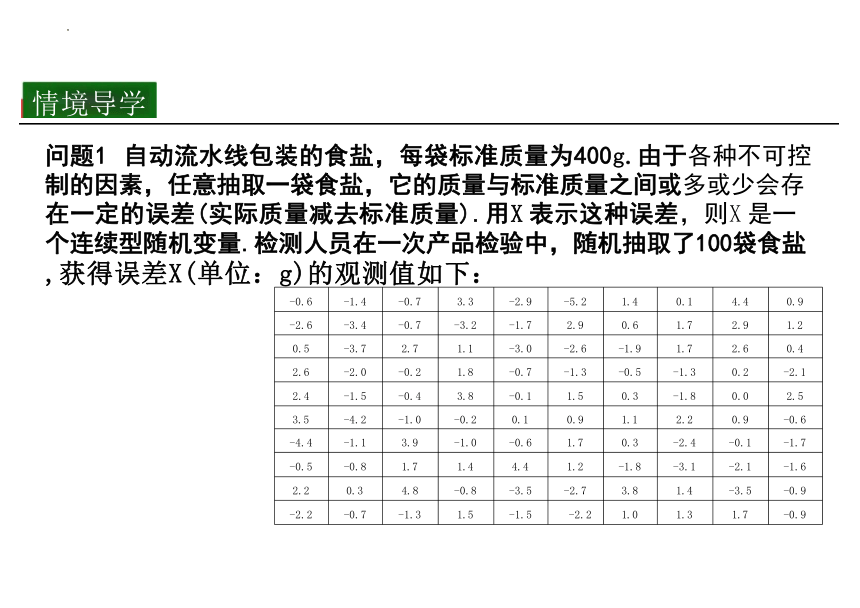
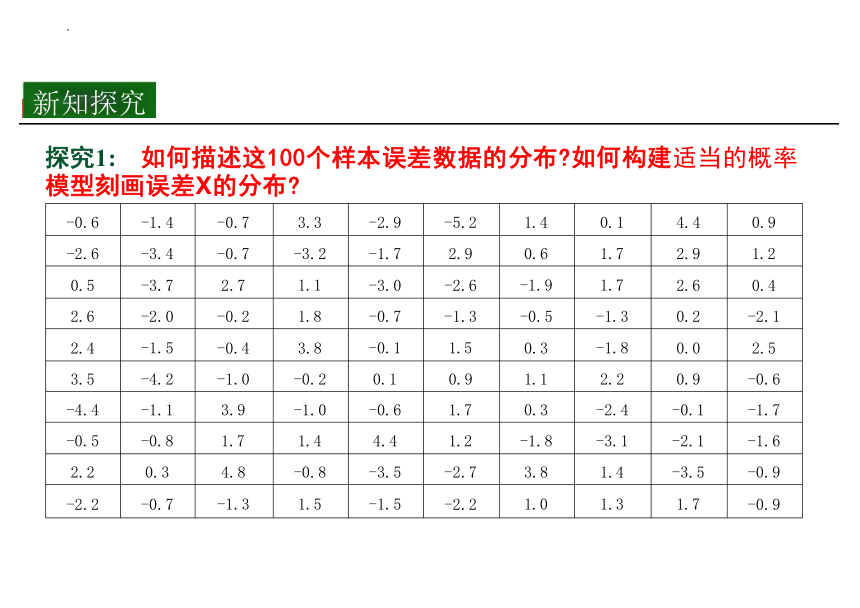
-0.6 -1.4 -0.7 3.3 -2.9 -5.2 1.4 0.1 4.4
0.9
-2.6 -3.4 -0.7 -3.2 -1.7 2.9 0.6 1.7 2.9
1.2
0.5 -3.7 2.7 1.1 -3.0 -2.6 -1.9 1.7 2.6
0.4
2.6 -2.0 -0.2 1.8 -0.7 -1.3 -0.5 -1.3 0.2
-2.1
2.4 -1.5 -0.4 3.8 -0.1 1.5 0.3 -1.8 0.0
2.5
3.5 -4.2 -1.0 -0.2 0.1 0.9 1.1 2.2 0.9
-0.6
-4.4 -1.1 3.9 -1.0 -0.6 1.7 0.3 -2.4 -0.1
-1.7
-0.5 -0.8 1.7 1.4 4.4 1.2 -1.8 -3.1 -2.1
-1.6
2.2 0.3 4.8 -0.8 -3.5 -2.7 3.8 1.4 -3.5
-0.9
-2.2 -0.7 -1.3 1.5 -1.5 -2.2 1.0 1.3 1.7
-0.9
问题1 自动流水线包装的食盐,每袋标准质量为400g.由于各种不可控 制的因素,任意抽取一袋食盐,它的质量与标准质量之间或多或少会存 在一定的误差(实际质量减去标准质量).用X 表示这种误差,则X 是一 个连续型随机变量.检测人员在一次产品检验中,随机抽取了100袋食盐 ,获得误差X(单位:g)的观测值如下:
情境导学
-0.6 -1.4 -0.7 3.3 -2.9 -5.2 1.4 0.1 4.4
0.9
-2.6 -3.4 -0.7 -3.2 -1.7 2.9 0.6 1.7 2.9
1.2
0.5 -3.7 2.7 1.1 -3.0 -2.6 -1.9 1.7 2.6
0.4
2.6 -2.0 -0.2 1.8 -0.7 -1.3 -0.5 -1.3 0.2
-2.1
2.4 -1.5 -0.4 3.8 -0.1 1.5 0.3 -1.8 0.0
2.5
3.5 -4.2 -1.0 -0.2 0.1 0.9 1.1 2.2 0.9
-0.6
-4.4 -1.1 3.9 -1.0 -0.6 1.7 0.3 -2.4 -0.1
-1.7
-0.5 -0.8 1.7 1.4 4.4 1.2 -1.8 -3.1 -2.1
-1.6
2.2 0.3 4.8 -0.8 -3.5 -2.7 3.8 1.4 -3.5
-0.9
-2.2 -0.7 -1.3 1.5 -1.5 -2.2 1.0 1.3 1.7
-0.9
探究1: 如何描述这100个样本误差数据的分布 如何构建适当的概率 模型刻画误差X的分布
新知探究
区间 频数 频率
频率/组距
探究1: 如何描述这100个样本误差数据的分布 如何构建适当的概率 模型刻画误差X的分布
新知探究
频率/组距
0.20
0.15
0.10
0.05
-6-4-2 0 2 4 0 X
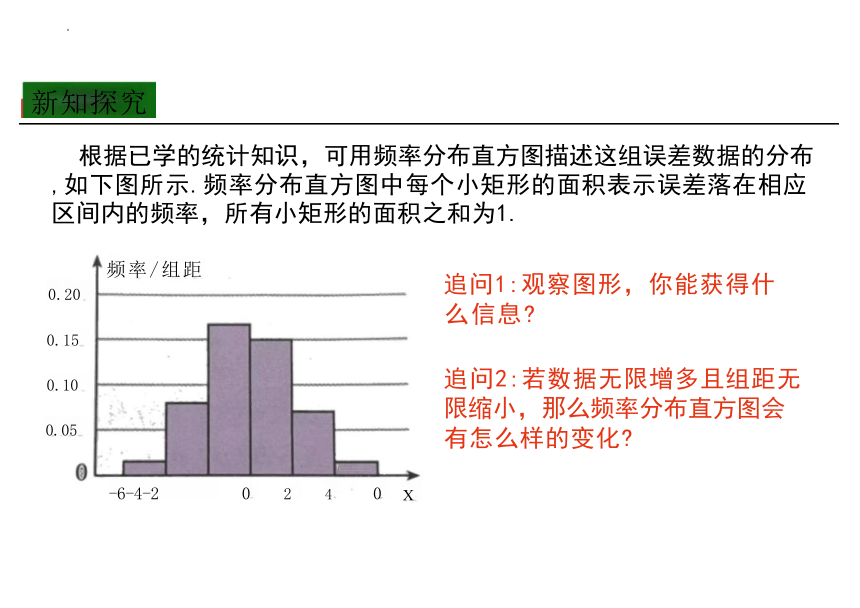
追问1:观察图形,你能获得什 么信息
追问2:若数据无限增多且组距无 限缩小,那么频率分布直方图会 有怎么样的变化
根据已学的统计知识,可用频率分布直方图描述这组误差数据的分布 ,如下图所示.频率分布直方图中每个小矩形的面积表示误差落在相应 区间内的频率,所有小矩形的面积之和为1.
新知探究
f(x)
0.20
0.15
0.10
0.05
0
-6-4-2 0 2 4 6 x
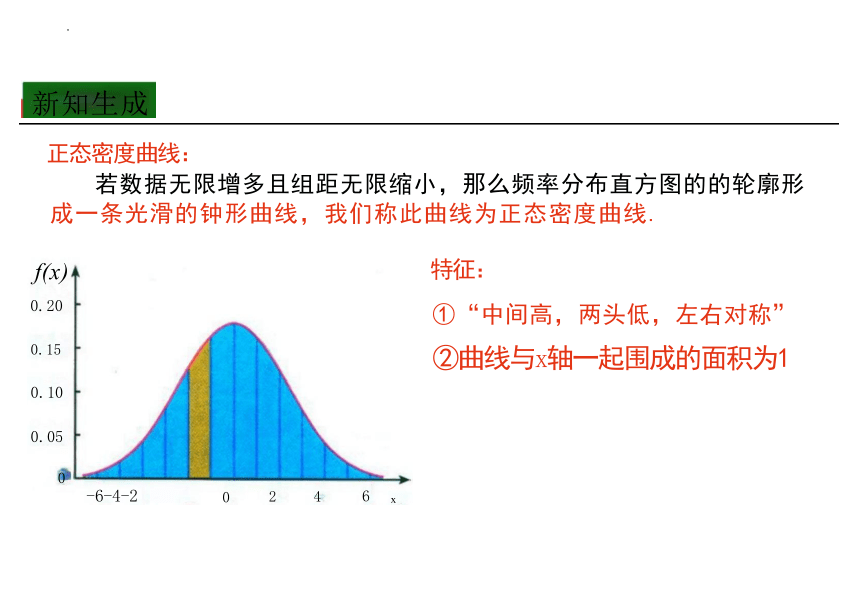
正态密度曲线:
若数据无限增多且组距无限缩小,那么频率分布直方图的的轮廓形
成一条光滑的钟形曲线,我们称此曲线为正态密度曲线.
特征:
①“中间高,两头低,左右对称”
②曲线与x轴一起围成的面积为1
新知生成
f(x)
0.20 0.15
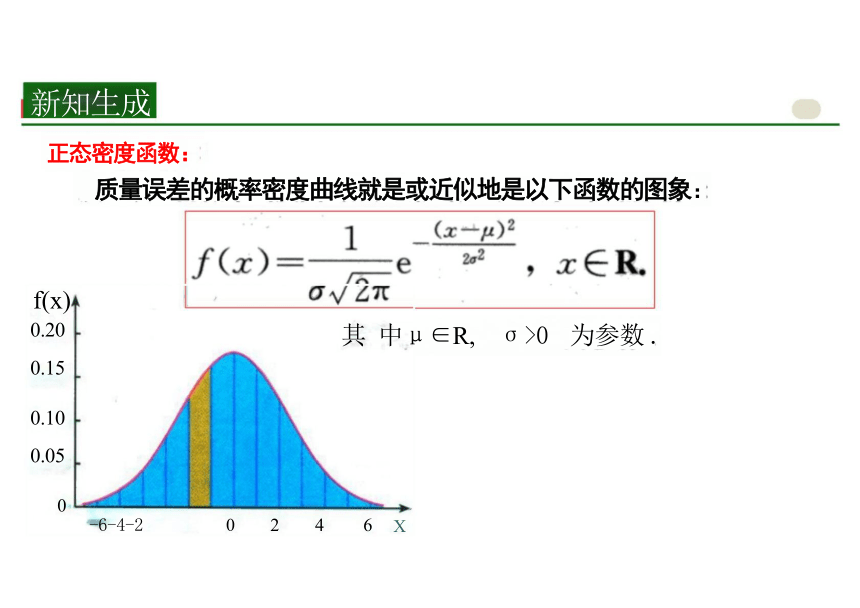
其 中μ∈R, σ>0 为参数 .
0.10 0.05
新知生成
正态密度函数:
质量误差的概率密度曲线就是或近似地是以下函数的图象:
0
-6-4-2 0 2 4 6 X
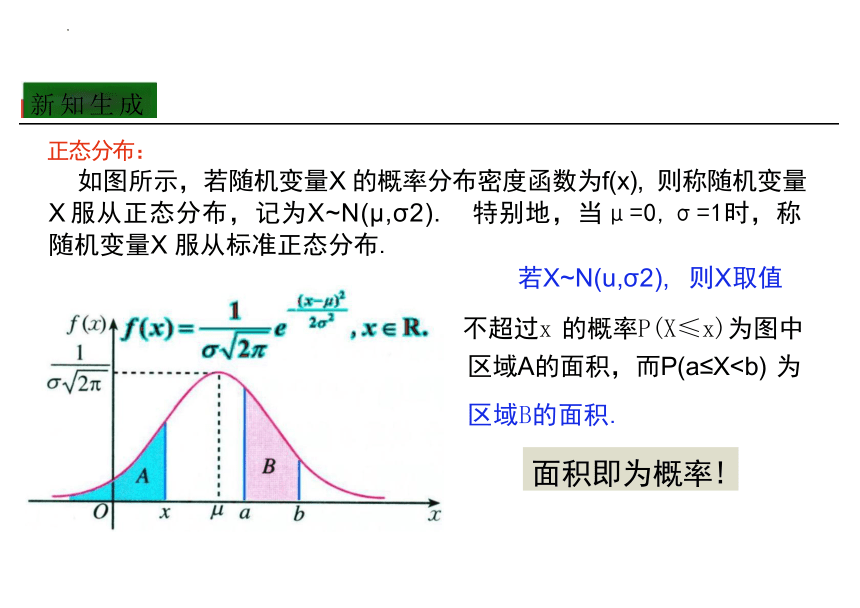
正态分布:
如图所示,若随机变量X 的概率分布密度函数为f(x), 则称随机变量 X 服从正态分布,记为X~N(μ,σ2). 特别地,当μ=0,σ=1时,称 随机变量X 服从标准正态分布.
若X~N(u,σ2), 则X取值
不超过x 的概率P(X≤x)为图中 区域A的面积,而P(a≤X区域B的面积.
面积即为概率!
新知生成
在实际中许多随机现象都服从或近似服从正态分布:
在生产中,在正常生产条件下各种产品的质量指标;
在测量中,测量结果;在生物学中,同一群体的某一特征, . . . ;
在气象中,某地每年七月份的平均气温、平均湿度以及降雨量等,水 文中的水位;
服从正态分布的随机变量叫做正态随机变量,简称正态变量.
新知生成
特点:(1)非负性:对Vx∈R,f(x)>0, 图象在x轴上方;
(2)对称性:曲线是单峰的,关于直线x=μ 对称;
(3)最大值:曲线在x=μ 处达到峰值
(4)曲线与x轴之间的区域的面积为1;
(5)当|x| 无限增大时,曲线无限接近x轴.
探究2:观察正态曲线及相应的密度函数,正态曲线有哪些特点
新知探究
探究3:一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线 的形状有何影响 它们反映正态分布的哪些特征
(1)当参数σ取定值时,观察μ对正态分布曲线的影响.
参数μ反映了正态分布的 集中位置,可以用均值来估 计,故有E(X)=μ .
值的变化而沿x 轴平移,故μ 称为位置参数;
f(x)
μ=0 μ=1
取σ=1
μ=-1
若σ固定,函数图像随μ
新知探究
0 X
若μ固定,σ大时,曲线“矮 胖”;σ小时,曲线“瘦 高”, 故 称σ为形状参数。
σ反映了随机变量分布相对于
均值μ的离散程度,可以用标准 差来估计,故有D(X)=σ .
X
探究3:一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线 的形状有何影响 它们反映正态分布的哪些特征
(2)当参数μ取定值时,观察σ对正态分布曲线的影响.
f(x) 个σ=0.5
σ=1
O=2
μ
新知探究
取μ=0
2、已知随机变量服从正态分布,其正
态曲线如图所示,则总体的均值μ=
,方差σ2=
,μ,σ(σ>0)都是实数
1、下列函数是正态密度函数的是( )
小试牛刀
A
●
密度曲线如图所示,下列说法中不正确的是(BCD)
A. 甲科总体的标准差最小
B. 丙科总体的平均数最小
C. 乙科总体的标准差及平均数都比甲小, 比丙大
D. 甲、乙、丙总体的平均数不相同
3、(多选)一次教学质量检测中,甲、乙、丙三科考试成绩的正态分布
小试牛刀
4、(多选)下面给出的关于正态曲线的4个叙述中,正确的有( ABD )
A.曲线在x轴上方,且与x轴不相交
B.当x>μ时,曲线下降,当x<μ时,曲线上升
C.当μ一定时,σ越小,总体分布越分散,σ越大,总体分布越集中
D.曲线关于直线x=μ对称,且当x=μ时,位于最高点
小试牛刀
例1:李明上学有时坐公交车,有时骑自行车.他各记录了50次坐公交车 和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30 min,
样本方差为36;骑自行车平均用时34 min, 样本方差为4.假设坐公交车 用时X 和骑自行车用时Y都服从正态分布.
(1)估计X,Y 的分布中的参数;
解:(1)随机变量X的样本均值为30,样本标准差为6;
随机变量Y的样本均值为34,样本标准差为2.
用样本均值估计参数μ,用样本标准差估计参数σ,可以得到:
X~N(30,6 ),Y~N(34,22)
典例剖析
例1:李明上学有时坐公交车,有时骑自行车.他各记录了50次坐公交车 和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30 min,
样本方差为36;骑自行车平均用时34 min, 样本方差为4.假设坐公交车 用时X 和骑自行车用时Y都服从正态分布.
(2)根据(1)中的估计结果,利用信息技术工具画出X和Y的分布密度
yA
Y的密度曲线
X的密度曲线
0 26303438 t/min
典例剖析
曲线;
例1:李明上学有时坐公交车,有时骑自行车.他各记录了50次坐公交车 和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30 min,
样本方差为36;骑自行车平均用时34 min, 样本方差为4.假设坐公交车 用时X和骑自行车用时Y都服从正态分布.
(3)如果某天有38 min 可用,李明应选择哪种交通工具 如果某天只 有34 min 可用,又应该选择哪种交通工具 请说明理由.
(3)Y的密度曲线X 的密度曲线 yA P(X≤38)P(X≤34)>P(Y≤34).
所以,如果有38min 可用,那么骑自行 X 的密度曲线 Y的密度曲线
车不迟到的概率大,应选择骑自行车;
如果只有34min 可用,那么坐公交车
不迟到的概率大,应选择坐公交车. 26303438 t/min
典例剖析
探究4:正态曲线下的面积规律:
(1)X 轴与正态曲线所夹面积恒等于1;
(2)对称区域面积相等,即概率相等.
S(-X ,-X ) S(x ,X )
-X -X μ X X
新知探究
μ-3σ μ-2o μ-σ μ μ+o μ+2σ μ+3o
k…68.27% …
… 95.45%…… …
…… …99.73%…… …
探究4:正态曲线下的面积规律:
假设X~N(μ,σ ), 可以证明:对给定的k∈N*, P(μ-ko≤X≤μ+ko)是一个只与k有关的定值.特别地,
(3)3σ原则:在实际应用中,服
从于正态分布的随机变量X只取
[μ-3σ,μ+3σ]中的值.
P(μ-oP(μ-2oP(μ-3σ新知探究
【例2】设s~N(1,4),试求:
(1)P(-1<ξ≤3);
(2)P(3(3)P(s≥5).
解:(1)∵ξ~N(1,4),
∴μ=1,σ=2,
P(-1≤ξ≤3)=P(1-2≤ξ≤1+2)
=P(μ-σ≤ξ≤μ+σ)≈0.6827.
典例剖析
(2)∵P(3≤ξ≤5)=P(-3≤ξ≤ 一1),
【例2】设s~N(1,4),试求:
(1)P(-1(2)P(3(3)P(s≥5).
典例剖析
【例2】设s~N(1,4),试求:
(1)P(-1(2)P(3(3)P(s≥5).
典例剖析
利用正态分布求概率的两个方法:
(1)对称法:由于正态曲线是关于直线x=μ对称的,且概率的和为1,
故关于直线x=μ对称的区间概率相等.如:
①P(X②P(X<μ-a)=P(X>μ+a).
(2)“3σ”法:利用X落在区间[μ- σ,μ+σ],[μ-2σ,μ+2σ],
[μ-3σ,μ+3σ]内的概率分别是0.6827,0.9545,0.9973求解.
归纳提升
(1)P(X>1)= ;(2)P(X>0)= ;
(3)P(X>2)= ; (4)P(X<2)= ;
(5)P(01.若X~N(1,o ),且 P(X<0)=a,则
-3-2-10 2 34 X
巩固练习
μ=1
y
2、设离散型随机变量X~N(0,1),则P(X≤0)= 0.5
P(-23. 若随机变量X~N(μ,o ), 且 P(X>6)=P(X <一2)=0.3,则
巩固练习
●
4、在某次数学考试中,考生的成绩X 服从正态分X~N(90,100).
(1)求考试成绩X 位于区间(70,110)上的概率是多少
(2)若此次考试共有2000名考生,试估计考试成绩在(80,100)间的考生大 约有多少人
巩固练习
正态分布密度曲线
正态分布密度曲线的特点
参数和σ对正态曲线的影响
正态分布的意义
30原则
课堂小结
高斯是一个伟大的数学家,一生中的重要贡献不胜枚举.德国的
10马克纸币上印有高斯的头像和正态分布的曲线,这就传达了一个信 息:在高斯的科学贡献中,对人类文明影响最大的是正态分布.
那么,什么是正态分布
正态分布的曲线有什么
特征
新课导入
学业标准
学科素养
1.通过误差模型,了解正态曲线、正态
分布的概念(重点). 2.通过借助具体实例的频率分布直方图, 了解正态分布的特征及曲线表示的含义 (重点).
1.通过正态分布相关概念的学习, 培养数学抽象等核心素养;
2.通过运用正态曲线的性质求随
3.了解正态分布的均值、方差及其含义 (难点).
机变量在某一区间的概率,提升数
学运算、直观想象等核心素养.
4.会用正态分布解决实际问题
学习目标
X 0 1 k
n
P
X 0 1 k
n
P
X 0
1
P
2、二项分布:X~B(n,p):
3、超几何分布:
复习旧知
1、两点分布:
生活中还有许多随机变量不是离散型的随机变量,例如:
①小明上学途中等公交车的时间X;
②实验中测量某零件尺寸的误差Y;
③秦皇岛5月份的降雨量Z;
④某电器的使用寿命;
●●
你还能举出几个这样的例子吗
连续型随机变量:
如果随机变量X的所有取值不可以逐个列举出来,而是充满某个 区间甚至整个实轴,但取一点的概率为0,我们称这类变量为连续型随 机变量。
情境导学
-0.6 -1.4 -0.7 3.3 -2.9 -5.2 1.4 0.1 4.4
0.9
-2.6 -3.4 -0.7 -3.2 -1.7 2.9 0.6 1.7 2.9
1.2
0.5 -3.7 2.7 1.1 -3.0 -2.6 -1.9 1.7 2.6
0.4
2.6 -2.0 -0.2 1.8 -0.7 -1.3 -0.5 -1.3 0.2
-2.1
2.4 -1.5 -0.4 3.8 -0.1 1.5 0.3 -1.8 0.0
2.5
3.5 -4.2 -1.0 -0.2 0.1 0.9 1.1 2.2 0.9
-0.6
-4.4 -1.1 3.9 -1.0 -0.6 1.7 0.3 -2.4 -0.1
-1.7
-0.5 -0.8 1.7 1.4 4.4 1.2 -1.8 -3.1 -2.1
-1.6
2.2 0.3 4.8 -0.8 -3.5 -2.7 3.8 1.4 -3.5
-0.9
-2.2 -0.7 -1.3 1.5 -1.5 -2.2 1.0 1.3 1.7
-0.9
问题1 自动流水线包装的食盐,每袋标准质量为400g.由于各种不可控 制的因素,任意抽取一袋食盐,它的质量与标准质量之间或多或少会存 在一定的误差(实际质量减去标准质量).用X 表示这种误差,则X 是一 个连续型随机变量.检测人员在一次产品检验中,随机抽取了100袋食盐 ,获得误差X(单位:g)的观测值如下:
情境导学
-0.6 -1.4 -0.7 3.3 -2.9 -5.2 1.4 0.1 4.4
0.9
-2.6 -3.4 -0.7 -3.2 -1.7 2.9 0.6 1.7 2.9
1.2
0.5 -3.7 2.7 1.1 -3.0 -2.6 -1.9 1.7 2.6
0.4
2.6 -2.0 -0.2 1.8 -0.7 -1.3 -0.5 -1.3 0.2
-2.1
2.4 -1.5 -0.4 3.8 -0.1 1.5 0.3 -1.8 0.0
2.5
3.5 -4.2 -1.0 -0.2 0.1 0.9 1.1 2.2 0.9
-0.6
-4.4 -1.1 3.9 -1.0 -0.6 1.7 0.3 -2.4 -0.1
-1.7
-0.5 -0.8 1.7 1.4 4.4 1.2 -1.8 -3.1 -2.1
-1.6
2.2 0.3 4.8 -0.8 -3.5 -2.7 3.8 1.4 -3.5
-0.9
-2.2 -0.7 -1.3 1.5 -1.5 -2.2 1.0 1.3 1.7
-0.9
探究1: 如何描述这100个样本误差数据的分布 如何构建适当的概率 模型刻画误差X的分布
新知探究
区间 频数 频率
频率/组距
探究1: 如何描述这100个样本误差数据的分布 如何构建适当的概率 模型刻画误差X的分布
新知探究
频率/组距
0.20
0.15
0.10
0.05
-6-4-2 0 2 4 0 X
追问1:观察图形,你能获得什 么信息
追问2:若数据无限增多且组距无 限缩小,那么频率分布直方图会 有怎么样的变化
根据已学的统计知识,可用频率分布直方图描述这组误差数据的分布 ,如下图所示.频率分布直方图中每个小矩形的面积表示误差落在相应 区间内的频率,所有小矩形的面积之和为1.
新知探究
f(x)
0.20
0.15
0.10
0.05
0
-6-4-2 0 2 4 6 x
正态密度曲线:
若数据无限增多且组距无限缩小,那么频率分布直方图的的轮廓形
成一条光滑的钟形曲线,我们称此曲线为正态密度曲线.
特征:
①“中间高,两头低,左右对称”
②曲线与x轴一起围成的面积为1
新知生成
f(x)
0.20 0.15
其 中μ∈R, σ>0 为参数 .
0.10 0.05
新知生成
正态密度函数:
质量误差的概率密度曲线就是或近似地是以下函数的图象:
0
-6-4-2 0 2 4 6 X
正态分布:
如图所示,若随机变量X 的概率分布密度函数为f(x), 则称随机变量 X 服从正态分布,记为X~N(μ,σ2). 特别地,当μ=0,σ=1时,称 随机变量X 服从标准正态分布.
若X~N(u,σ2), 则X取值
不超过x 的概率P(X≤x)为图中 区域A的面积,而P(a≤X
面积即为概率!
新知生成
在实际中许多随机现象都服从或近似服从正态分布:
在生产中,在正常生产条件下各种产品的质量指标;
在测量中,测量结果;在生物学中,同一群体的某一特征, . . . ;
在气象中,某地每年七月份的平均气温、平均湿度以及降雨量等,水 文中的水位;
服从正态分布的随机变量叫做正态随机变量,简称正态变量.
新知生成
特点:(1)非负性:对Vx∈R,f(x)>0, 图象在x轴上方;
(2)对称性:曲线是单峰的,关于直线x=μ 对称;
(3)最大值:曲线在x=μ 处达到峰值
(4)曲线与x轴之间的区域的面积为1;
(5)当|x| 无限增大时,曲线无限接近x轴.
探究2:观察正态曲线及相应的密度函数,正态曲线有哪些特点
新知探究
探究3:一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线 的形状有何影响 它们反映正态分布的哪些特征
(1)当参数σ取定值时,观察μ对正态分布曲线的影响.
参数μ反映了正态分布的 集中位置,可以用均值来估 计,故有E(X)=μ .
值的变化而沿x 轴平移,故μ 称为位置参数;
f(x)
μ=0 μ=1
取σ=1
μ=-1
若σ固定,函数图像随μ
新知探究
0 X
若μ固定,σ大时,曲线“矮 胖”;σ小时,曲线“瘦 高”, 故 称σ为形状参数。
σ反映了随机变量分布相对于
均值μ的离散程度,可以用标准 差来估计,故有D(X)=σ .
X
探究3:一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线 的形状有何影响 它们反映正态分布的哪些特征
(2)当参数μ取定值时,观察σ对正态分布曲线的影响.
f(x) 个σ=0.5
σ=1
O=2
μ
新知探究
取μ=0
2、已知随机变量服从正态分布,其正
态曲线如图所示,则总体的均值μ=
,方差σ2=
,μ,σ(σ>0)都是实数
1、下列函数是正态密度函数的是( )
小试牛刀
A
●
密度曲线如图所示,下列说法中不正确的是(BCD)
A. 甲科总体的标准差最小
B. 丙科总体的平均数最小
C. 乙科总体的标准差及平均数都比甲小, 比丙大
D. 甲、乙、丙总体的平均数不相同
3、(多选)一次教学质量检测中,甲、乙、丙三科考试成绩的正态分布
小试牛刀
4、(多选)下面给出的关于正态曲线的4个叙述中,正确的有( ABD )
A.曲线在x轴上方,且与x轴不相交
B.当x>μ时,曲线下降,当x<μ时,曲线上升
C.当μ一定时,σ越小,总体分布越分散,σ越大,总体分布越集中
D.曲线关于直线x=μ对称,且当x=μ时,位于最高点
小试牛刀
例1:李明上学有时坐公交车,有时骑自行车.他各记录了50次坐公交车 和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30 min,
样本方差为36;骑自行车平均用时34 min, 样本方差为4.假设坐公交车 用时X 和骑自行车用时Y都服从正态分布.
(1)估计X,Y 的分布中的参数;
解:(1)随机变量X的样本均值为30,样本标准差为6;
随机变量Y的样本均值为34,样本标准差为2.
用样本均值估计参数μ,用样本标准差估计参数σ,可以得到:
X~N(30,6 ),Y~N(34,22)
典例剖析
例1:李明上学有时坐公交车,有时骑自行车.他各记录了50次坐公交车 和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30 min,
样本方差为36;骑自行车平均用时34 min, 样本方差为4.假设坐公交车 用时X 和骑自行车用时Y都服从正态分布.
(2)根据(1)中的估计结果,利用信息技术工具画出X和Y的分布密度
yA
Y的密度曲线
X的密度曲线
0 26303438 t/min
典例剖析
曲线;
例1:李明上学有时坐公交车,有时骑自行车.他各记录了50次坐公交车 和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30 min,
样本方差为36;骑自行车平均用时34 min, 样本方差为4.假设坐公交车 用时X和骑自行车用时Y都服从正态分布.
(3)如果某天有38 min 可用,李明应选择哪种交通工具 如果某天只 有34 min 可用,又应该选择哪种交通工具 请说明理由.
(3)Y的密度曲线X 的密度曲线 yA P(X≤38)
所以,如果有38min 可用,那么骑自行 X 的密度曲线 Y的密度曲线
车不迟到的概率大,应选择骑自行车;
如果只有34min 可用,那么坐公交车
不迟到的概率大,应选择坐公交车. 26303438 t/min
典例剖析
探究4:正态曲线下的面积规律:
(1)X 轴与正态曲线所夹面积恒等于1;
(2)对称区域面积相等,即概率相等.
S(-X ,-X ) S(x ,X )
-X -X μ X X
新知探究
μ-3σ μ-2o μ-σ μ μ+o μ+2σ μ+3o
k…68.27% …
… 95.45%…… …
…… …99.73%…… …
探究4:正态曲线下的面积规律:
假设X~N(μ,σ ), 可以证明:对给定的k∈N*, P(μ-ko≤X≤μ+ko)是一个只与k有关的定值.特别地,
(3)3σ原则:在实际应用中,服
从于正态分布的随机变量X只取
[μ-3σ,μ+3σ]中的值.
P(μ-o
【例2】设s~N(1,4),试求:
(1)P(-1<ξ≤3);
(2)P(3
解:(1)∵ξ~N(1,4),
∴μ=1,σ=2,
P(-1≤ξ≤3)=P(1-2≤ξ≤1+2)
=P(μ-σ≤ξ≤μ+σ)≈0.6827.
典例剖析
(2)∵P(3≤ξ≤5)=P(-3≤ξ≤ 一1),
【例2】设s~N(1,4),试求:
(1)P(-1
典例剖析
【例2】设s~N(1,4),试求:
(1)P(-1
典例剖析
利用正态分布求概率的两个方法:
(1)对称法:由于正态曲线是关于直线x=μ对称的,且概率的和为1,
故关于直线x=μ对称的区间概率相等.如:
①P(X
(2)“3σ”法:利用X落在区间[μ- σ,μ+σ],[μ-2σ,μ+2σ],
[μ-3σ,μ+3σ]内的概率分别是0.6827,0.9545,0.9973求解.
归纳提升
(1)P(X>1)= ;(2)P(X>0)= ;
(3)P(X>2)= ; (4)P(X<2)= ;
(5)P(0
-3-2-10 2 34 X
巩固练习
μ=1
y
2、设离散型随机变量X~N(0,1),则P(X≤0)= 0.5
P(-2
巩固练习
●
4、在某次数学考试中,考生的成绩X 服从正态分X~N(90,100).
(1)求考试成绩X 位于区间(70,110)上的概率是多少
(2)若此次考试共有2000名考生,试估计考试成绩在(80,100)间的考生大 约有多少人
巩固练习
正态分布密度曲线
正态分布密度曲线的特点
参数和σ对正态曲线的影响
正态分布的意义
30原则
课堂小结
