2024-2025学年人教版八年级上册数学全等三角形辅助线专题 01专题 全等三角形含辅助线证明题(中线倍长)(无答案)
文档属性
| 名称 | 2024-2025学年人教版八年级上册数学全等三角形辅助线专题 01专题 全等三角形含辅助线证明题(中线倍长)(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-16 10:37:42 | ||
图片预览

文档简介
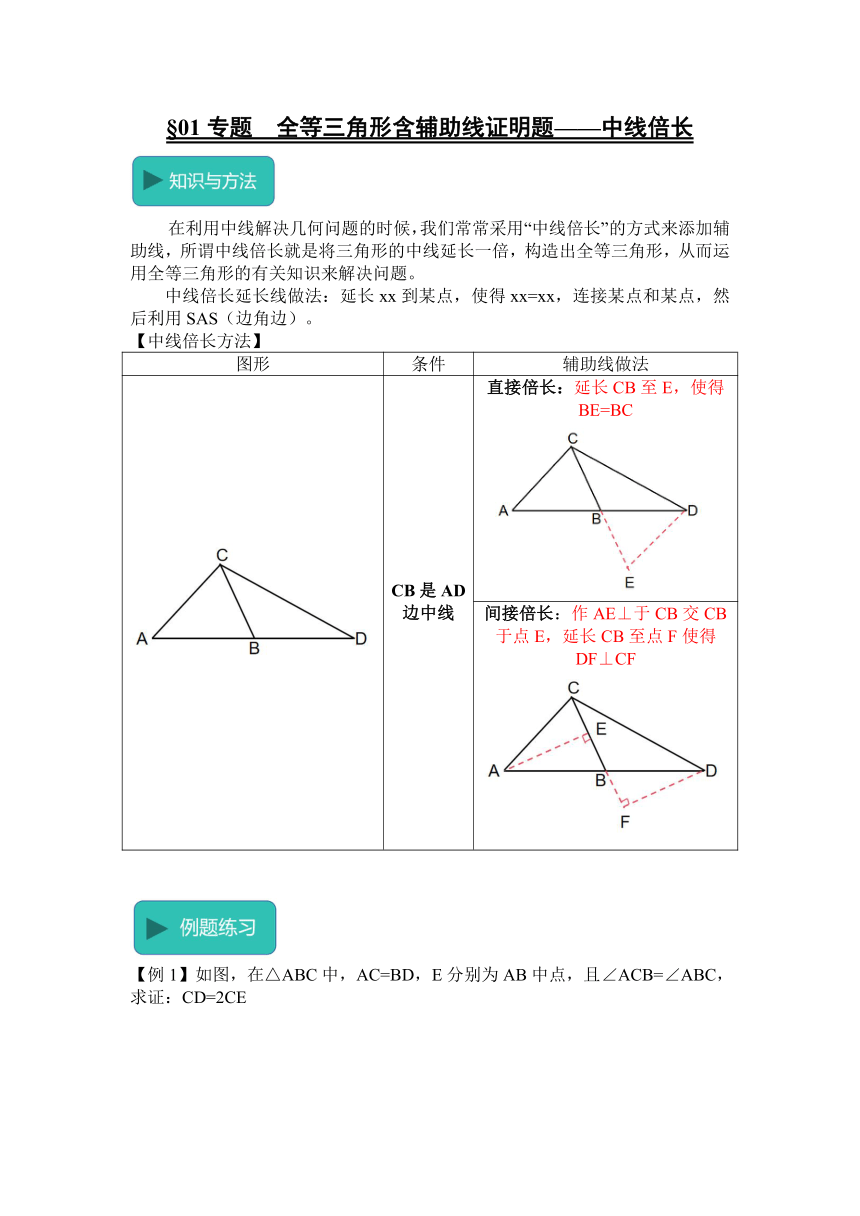
§01专题 全等三角形含辅助线证明题——中线倍长
在利用中线解决几何问题的时候,我们常常采用“中线倍长”的方式来添加辅助线,所谓中线倍长就是将三角形的中线延长一倍,构造出全等三角形,从而运用全等三角形的有关知识来解决问题。
中线倍长延长线做法:延长xx到某点,使得xx=xx,连接某点和某点,然后利用SAS(边角边)。
【中线倍长方法】
图形 条件 辅助线做法
CB是AD边中线 直接倍长:延长CB至E,使得BE=BC
间接倍长:作AE⊥于CB交CB于点E,延长CB至点F使得DF⊥CF
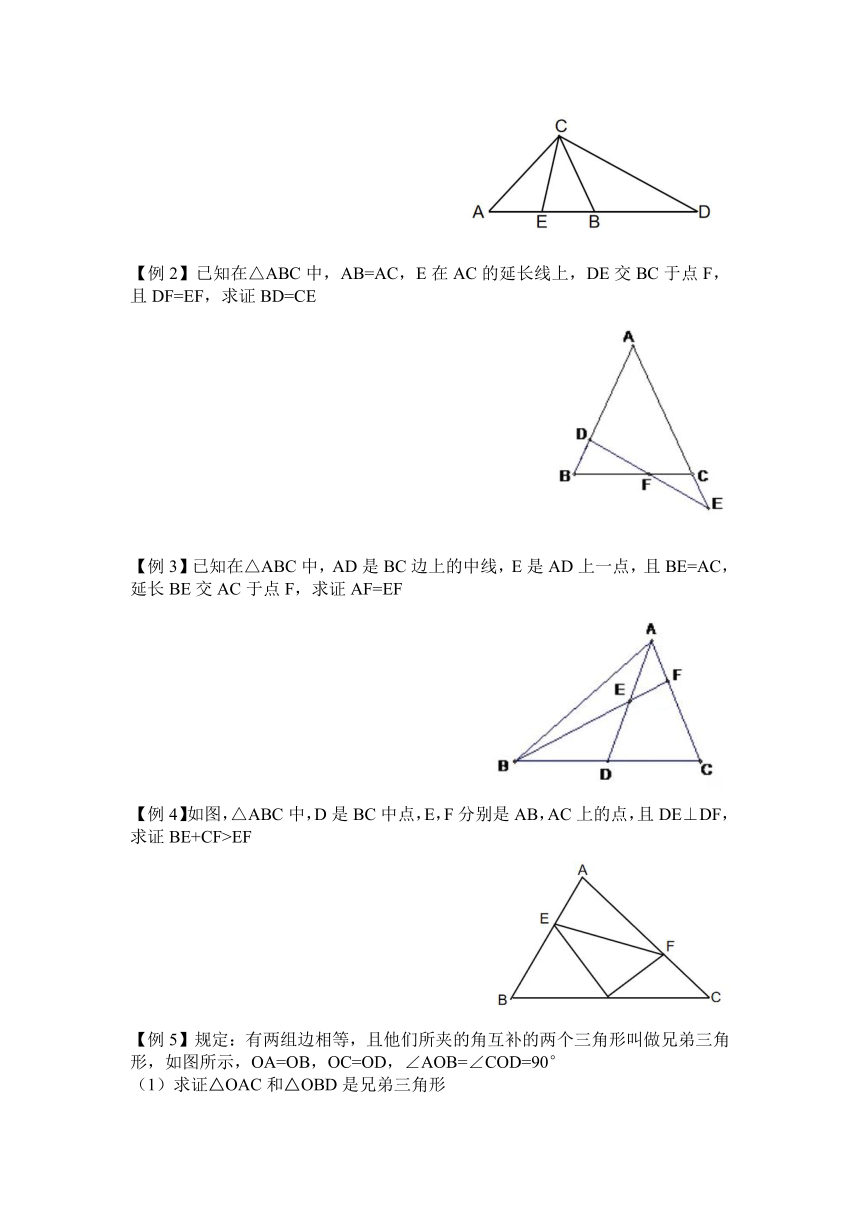
【例1】如图,在△ABC中,AC=BD,E分别为AB中点,且∠ACB=∠ABC,求证:CD=2CE
【例2】已知在△ABC中,AB=AC,E在AC的延长线上,DE交BC于点F,且DF=EF,求证BD=CE
【例3】已知在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于点F,求证AF=EF
【例4】如图,△ABC中,D是BC中点,E,F分别是AB,AC上的点,且DE⊥DF,求证BE+CF>EF
【例5】规定:有两组边相等,且他们所夹的角互补的两个三角形叫做兄弟三角形,如图所示,OA=OB,OC=OD,∠AOB=∠COD=90°
求证△OAC和△OBD是兄弟三角形
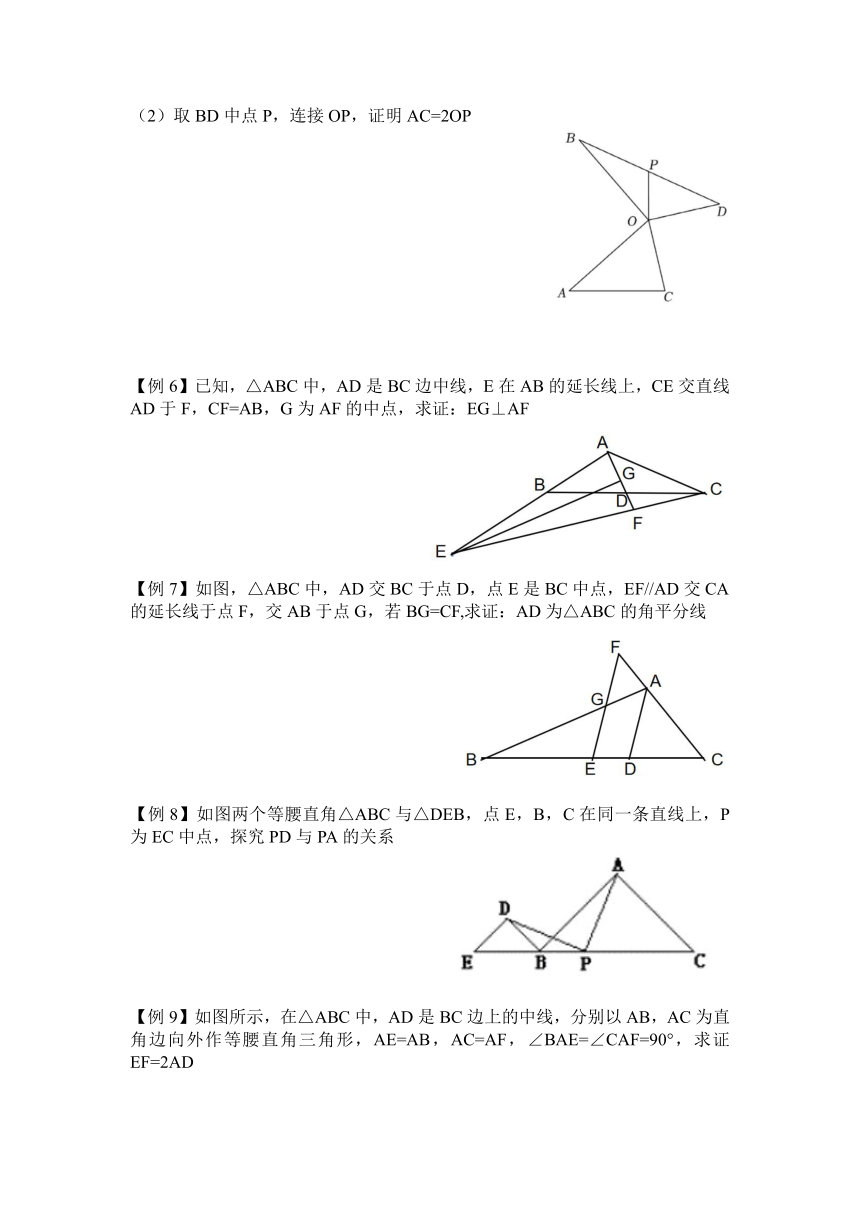
取BD中点P,连接OP,证明AC=2OP
【例6】已知,△ABC中,AD是BC边中线,E在AB的延长线上,CE交直线AD于F,CF=AB,G为AF的中点,求证:EG⊥AF
【例7】如图,△ABC中,AD交BC于点D,点E是BC中点,EF//AD交CA的延长线于点F,交AB于点G,若BG=CF,求证:AD为△ABC的角平分线
【例8】如图两个等腰直角△ABC与△DEB,点E,B,C在同一条直线上,P为EC中点,探究PD与PA的关系
【例9】如图所示,在△ABC中,AD是BC边上的中线,分别以AB,AC为直角边向外作等腰直角三角形,AE=AB,AC=AF,∠BAE=∠CAF=90°,求证EF=2AD
【例10】如图所示,在正方形ABCD的边CB的延长线上取一点E,△FEB为等腰直角三角形,∠FEB=90°,连接FD,取FD的中点G,连接EG,CG,求证:ED=CG且EG⊥CG
【例11】已知△ABC中,
如图1,点E为BC的中点,连AE并延长到点F,使得FE=EA,则BF与AC的数量关系是
如图2,若AB=AC,点E为边AC上的一点,过点C作BC的垂线交BE的延长线于点D,连接AD,若∠DAC=∠ABD,求证:AE=EC
如图3,点D在△ABC内部,且满足AD=BC,∠BAD=∠DCB,点M在DC的延长线上,连接AM交BD的延长线于点N,若点N为AM的中点,求证:DM=AB
【练1】如图在 △ABC中,AB>AC,∠1=∠2,P为AD上任意一点,,求证AB-AC>PB-PC
【练2】如图,△ACD中,B是AD中点,且AC=AB,求证:
∠D=∠ACE
CD=2CE
【练3】如图所示,已知△ABC中,AD平分∠ABC,E,F分别在BD,AD上,DE=CD,EF=AC,求证EF//AB
【练4】如图所示,O为四边形ABCD内部一点,E为AB的中点,OA=OD,OB=OC,∠AOB+∠COD=180°
若∠BOE=交BAO,AB=2,求OB的长
用等式表示线段OE与CD之间的关系,并证明
在利用中线解决几何问题的时候,我们常常采用“中线倍长”的方式来添加辅助线,所谓中线倍长就是将三角形的中线延长一倍,构造出全等三角形,从而运用全等三角形的有关知识来解决问题。
中线倍长延长线做法:延长xx到某点,使得xx=xx,连接某点和某点,然后利用SAS(边角边)。
【中线倍长方法】
图形 条件 辅助线做法
CB是AD边中线 直接倍长:延长CB至E,使得BE=BC
间接倍长:作AE⊥于CB交CB于点E,延长CB至点F使得DF⊥CF
【例1】如图,在△ABC中,AC=BD,E分别为AB中点,且∠ACB=∠ABC,求证:CD=2CE
【例2】已知在△ABC中,AB=AC,E在AC的延长线上,DE交BC于点F,且DF=EF,求证BD=CE
【例3】已知在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于点F,求证AF=EF
【例4】如图,△ABC中,D是BC中点,E,F分别是AB,AC上的点,且DE⊥DF,求证BE+CF>EF
【例5】规定:有两组边相等,且他们所夹的角互补的两个三角形叫做兄弟三角形,如图所示,OA=OB,OC=OD,∠AOB=∠COD=90°
求证△OAC和△OBD是兄弟三角形
取BD中点P,连接OP,证明AC=2OP
【例6】已知,△ABC中,AD是BC边中线,E在AB的延长线上,CE交直线AD于F,CF=AB,G为AF的中点,求证:EG⊥AF
【例7】如图,△ABC中,AD交BC于点D,点E是BC中点,EF//AD交CA的延长线于点F,交AB于点G,若BG=CF,求证:AD为△ABC的角平分线
【例8】如图两个等腰直角△ABC与△DEB,点E,B,C在同一条直线上,P为EC中点,探究PD与PA的关系
【例9】如图所示,在△ABC中,AD是BC边上的中线,分别以AB,AC为直角边向外作等腰直角三角形,AE=AB,AC=AF,∠BAE=∠CAF=90°,求证EF=2AD
【例10】如图所示,在正方形ABCD的边CB的延长线上取一点E,△FEB为等腰直角三角形,∠FEB=90°,连接FD,取FD的中点G,连接EG,CG,求证:ED=CG且EG⊥CG
【例11】已知△ABC中,
如图1,点E为BC的中点,连AE并延长到点F,使得FE=EA,则BF与AC的数量关系是
如图2,若AB=AC,点E为边AC上的一点,过点C作BC的垂线交BE的延长线于点D,连接AD,若∠DAC=∠ABD,求证:AE=EC
如图3,点D在△ABC内部,且满足AD=BC,∠BAD=∠DCB,点M在DC的延长线上,连接AM交BD的延长线于点N,若点N为AM的中点,求证:DM=AB
【练1】如图在 △ABC中,AB>AC,∠1=∠2,P为AD上任意一点,,求证AB-AC>PB-PC
【练2】如图,△ACD中,B是AD中点,且AC=AB,求证:
∠D=∠ACE
CD=2CE
【练3】如图所示,已知△ABC中,AD平分∠ABC,E,F分别在BD,AD上,DE=CD,EF=AC,求证EF//AB
【练4】如图所示,O为四边形ABCD内部一点,E为AB的中点,OA=OD,OB=OC,∠AOB+∠COD=180°
若∠BOE=交BAO,AB=2,求OB的长
用等式表示线段OE与CD之间的关系,并证明
