2024年甘肃省兰州市中考数学真题(无答案)
文档属性
| 名称 | 2024年甘肃省兰州市中考数学真题(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 422.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-16 10:27:55 | ||
图片预览


文档简介
2024年甘肃省兰州市中考数学试题
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.2024的绝对值是( )
A.﹣2024 B.2024 C. D.
2.若∠A=80°,则∠A的补角是( )
A.100° B.80° C.40° D.10°
3.2024年一季度,兰州市坚持稳中求进、综合施策,全市国民经济起步平稳,开局良好.一季度全市地区生产总值87790000000元,数据87790000000用科学记数法表示为( )
A.87.79×109 B.8.779×109
C.8.779×1010 D.8.779×1011
4.计算:2a(a﹣1)﹣2a2=( )
A.a B.﹣a C.2a D.﹣2a
5.一次函数y=2x﹣3的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.如图,小明在地图上量得∠1=∠2,由此判断幸福大街与平安大街互相平行,他判断的依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.对顶角相等
7.如图,小张想估测被池塘隔开的A,B两处景观之间的距离,他先在AB外取一点C,然后步测出AC,BC的中点D,E,并步测出DE的长约为18m,由此估测A,B之间的距离约为( )
A.18m B.24m C.36m D.54m
8.七巧板、九连环、华容道、鲁班锁是深受大家喜爱的益智玩具.现将1个七巧板,2个九连环,1个华容道,2个鲁班锁分别装在6个不透明的盒子中(每个盒子装1个),所有盒子除里面的玩具外均相同.从这6个盒子中随机抽取1个盒子,抽中七巧板的概率是( )
A. B. C. D.
9.关于x的一元二次方程9x2﹣6x+c=0有两个相等的实数根,则c=( )
A.﹣9 B.4 C.﹣1 D.1
10.数学家朱世杰所著的《四元玉鉴》是中国元代重要的数学著作之一,书中记载着这样一个问题,大意是:999文钱买了甜果和苦果共1000个,11文钱可买9个甜果,4文钱可买7个苦果,问甜果,苦果各买了多少个?设买了甜果x个,苦果y个,则可列方程组为( )
A.
B.
C.
D.
11.如图,在△ABC中,AB=AC,∠BAC=130°,DA⊥AC,则∠ADB=( )
A.100° B.115° C.130° D.145°
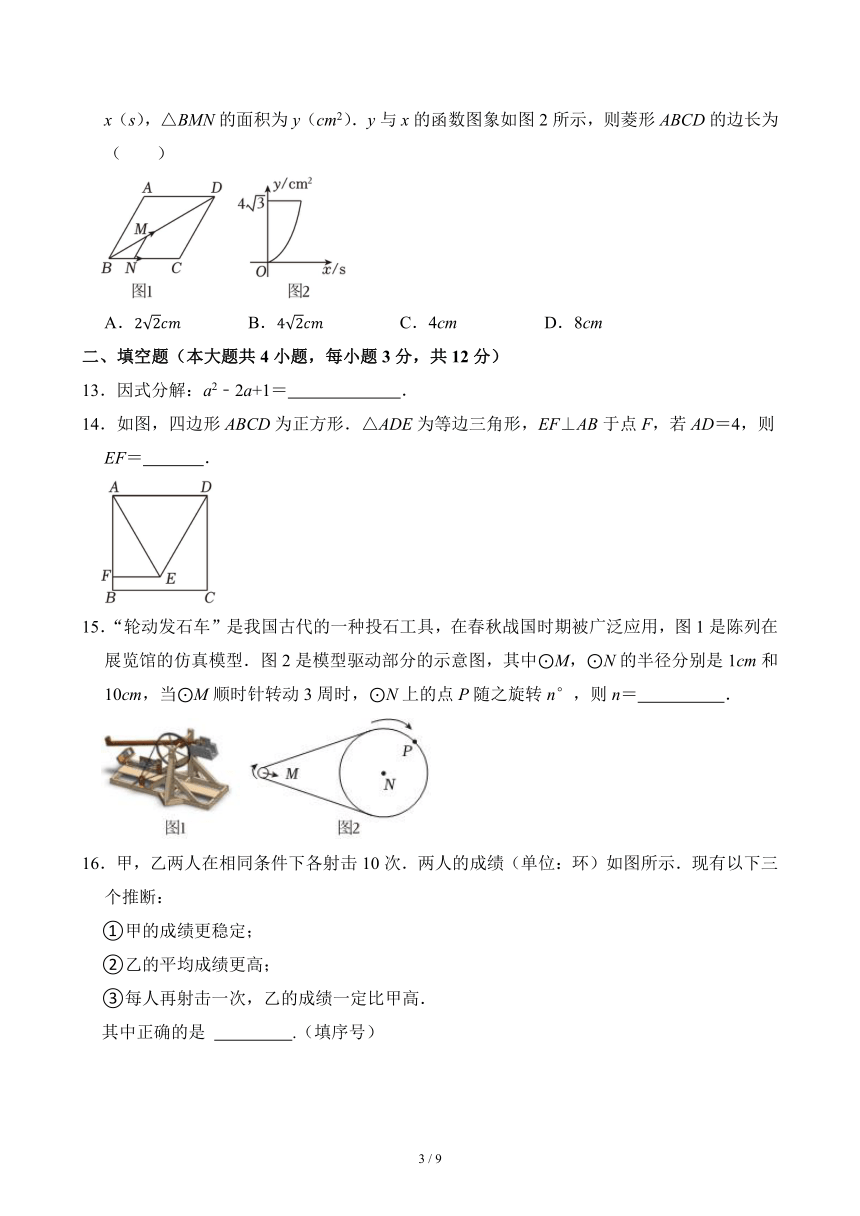
12.如图1,在菱形ABCD中,∠ABC=60°,连接BD,点M从B出发沿BD方向以的速度运动至D,同时点N从B出发沿BC方向以1cm/s的速度运动至C,设运动时间为x(s),△BMN的面积为y(cm2).y与x的函数图象如图2所示,则菱形ABCD的边长为( )
A. B. C.4cm D.8cm
二、填空题(本大题共4小题,每小题3分,共12分)
13.因式分解:a2﹣2a+1= .
14.如图,四边形ABCD为正方形.△ADE为等边三角形,EF⊥AB于点F,若AD=4,则EF= .
15.“轮动发石车”是我国古代的一种投石工具,在春秋战国时期被广泛应用,图1是陈列在展览馆的仿真模型.图2是模型驱动部分的示意图,其中⊙M,⊙N的半径分别是1cm和10cm,当⊙M顺时针转动3周时,⊙N上的点P随之旋转n°,则n= .
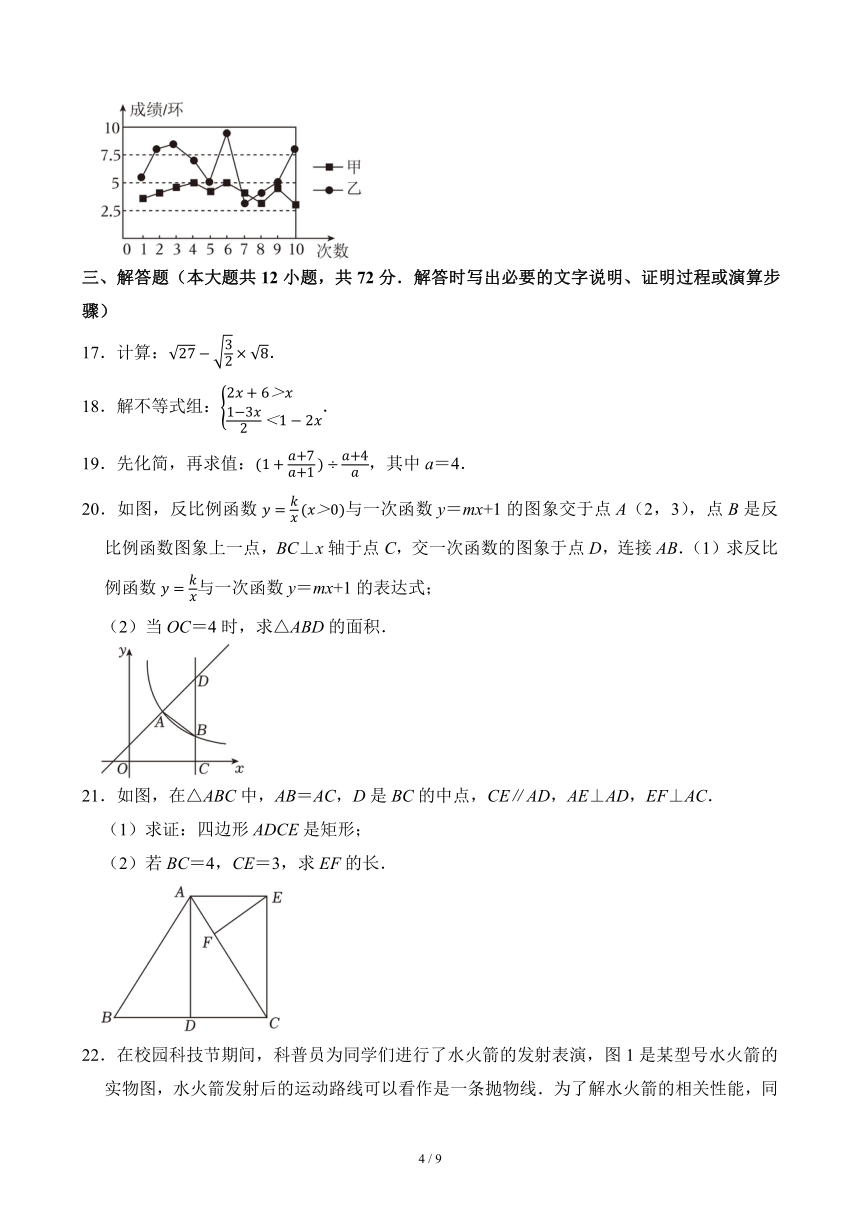
16.甲,乙两人在相同条件下各射击10次.两人的成绩(单位:环)如图所示.现有以下三个推断:
①甲的成绩更稳定;
②乙的平均成绩更高;
③每人再射击一次,乙的成绩一定比甲高.
其中正确的是 .(填序号)
三、解答题(本大题共12小题,共72分.解答时写出必要的文字说明、证明过程或演算步骤)
17.计算:.
18.解不等式组:.
19.先化简,再求值:,其中a=4.
20.如图,反比例函数与一次函数y=mx+1的图象交于点A(2,3),点B是反比例函数图象上一点,BC⊥x轴于点C,交一次函数的图象于点D,连接AB.(1)求反比例函数与一次函数y=mx+1的表达式;
(2)当OC=4时,求△ABD的面积.
21.如图,在△ABC中,AB=AC,D是BC的中点,CE∥AD,AE⊥AD,EF⊥AC.
(1)求证:四边形ADCE是矩形;
(2)若BC=4,CE=3,求EF的长.
22.在校园科技节期间,科普员为同学们进行了水火箭的发射表演,图1是某型号水火箭的实物图,水火箭发射后的运动路线可以看作是一条抛物线.为了解水火箭的相关性能,同学们进一步展开研究.如图2建立直角坐标系.水火箭发射后落在水平地面A处.科普员提供了该型号水火箭与地面成一定角度时,从发射到着陆过程中,水火箭距离地面OA的竖直高度y(m)与离发射点O的水平距离x(m)的几组关系数据如下:
水平距离x(m) 0 3 4 10 15 20 22 27
竖直高度y(m) 0 3.24 4.16 8 9 8 7.04 3.24
(1)根据如表,请确定抛物线的表达式;
(2)请计算当水火箭飞行至离发射点O的水平距离为5m时,水火箭距离地面的竖直高度.
23.观察发现:劳动人民在生产生活中创造了很多取材简单又便于操作的方法,正如木匠刘师傅的“木条画直角法”.如图1,他用木条能快速画出一个以点A为顶点的直角,具体作法如下:
①木条的两端分别记为点M,N,先将木条的端点M与点A重合,任意摆放木条后,另一个端点N的位置记为点B,连接AB;
②木条的端点N固定在点B处,将木条绕点B顺时针旋转一定的角度,端点M的落点记为点C(点A,B,C不在同一条直线上);
③连接CB并延长,将木条沿点C到点B的方向平移,使得端点M与点B重合,端点N在CB延长线上的落点记为点D;
④用另一根足够长的木条画线,连接AD,AC,则画出的∠DAC是直角.
操作体验:(1)根据“观察发现”中的信息重现刘师傅的画法.如图2,BA=BC.请画出以点A为顶点的直角,记作∠DAC;
推理论证:(2)如图1,小亮尝试揭示此操作的数学原理,请你补全括号里的证明依据:
证明:∵AB=BC=BD,
∴△ABC与△ABD是等腰三角形.
∴∠BCA=∠BAC,∠BDA=∠BAD.(依据1)
∴∠BCA+∠BDA=∠BAC+∠BAD=∠DAC.
∵∠DAC+∠BCA+∠BDA=180°,(依据2)
∴2∠DAC=180°.
∴∠DAC=90°.
依据1: :依据2: ;
拓展探究:(3)小亮进一步研究发现,用这种方法作直角存在一定的误差,用平时学习的尺规作图的方法可以减少误差.如图3,点O在直线l上,请用无刻度的直尺和圆规在图3中作出一个以O为顶点的直角,记作∠POQ,使得直角边OP(或OQ)在直线l上.(保留作图痕迹,不写作法)
24.为落实“双减”政策,培养德智体美劳全面发展的时代新人,某校组织调研学生体育和美育发展水平.现从七年级共180名学生中随机抽取20名学生,对每位学生的体育和美育水平进行测评后按百分制分数量化,并进行等级评定(成绩用x表示,分为四个等级,包括优秀:90≤x≤100;良好:80≤x<90;合格:70≤x<80;待提高:x<70).对数据进行整理,描述和分析,部分信息如下.
信息一:体育成绩的人数(频数)分布图如图.
信息二:美育成绩的人数(频数)分布表如下.
分组 90≤x≤100 80≤x<90 70≤x<80 x<70
人数 m 7 2 7
信息三:20位学生的体育成绩和美育成绩得分统计如下(共20个点).
根据以上信息,回答下列问题:
(1)填空:m= ;
(2)下列结论正确的是 ;(填序号)
①体育成绩低于80分的人数占抽取人数的40%;
②参与测评的20名学生美育成绩的中位数对应的等级是“合格”;
③在信息三中,相比于点A所代表的学生,点B所代表的学生的体育水平与其大致相同,但美育水平还存在一定差距,需要进一步提升;
(3)请结合以上信息,估计七年级全体学生中体育和美育两项成绩均属于“优秀”等级的人数.
25.单摆是一种能够产生往复摆动的装置.某兴趣小组利用摆球和摆线进行与单摆相关的实验探究,并撰写实验报告如下.
实验主题 探究摆球运动过程中高度的变化
实验用具 摆球,摆线,支架,摄像机等
实验说明 如图1,在支架的横杆点O处用摆线悬挂一个摆球,将摆球拉高后松手,摆球开始往复运动.(摆线的长度变化忽略不计) 如图2,摆球静止时的位置为点A,拉紧摆线将摆球拉至点B处,BD⊥OA.∠BOA=64°,BD=20.5cm;当摆球运动至点C时,∠COA=37°,CE⊥OA.(点O,A,B,C,D,E在同一平面内)
实验图示
解决问题:根据以上信息,求ED的长.(结果精确到0.1cm)
参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05.
26.如图,△ABC内接于⊙O,AB为⊙O的直径,点D为⊙O上一点,BC=BD,延长BA至E,使得∠ADE=∠CBA.
(1)求证:ED是⊙O的切线;
(2)若BO=4,,求ED的长.
27.综合与实践
【问题情境】在数学综合实践课上,同学们以特殊三角形为背景.探究动点运动的几何问题.如图,在△ABC中,点M,N分别为AB,AC上的动点(不含端点),且AN=BM.
【初步尝试】(1)如图1,当△ABC为等边三角形时,小颜发现:将MA绕点M逆时针旋转120°得到MD,连接BD,则MN=DB,请思考并证明;
【类比探究】(2)小梁尝试改变三角形的形状后进一步探究:如图2,在△ABC中,AB=AC,∠BAC=90°,AE⊥MN于点E,交BC于点F,将MA绕点M逆时针旋转90°得到MD,连接DA,DB.试猜想四边形AFBD的形状,并说明理由;
【拓展延伸】(3)孙老师提出新的探究方向:如图3,在△ABC中,AB=AC=4,∠BAC=90°,连接BN,CM,请直接写出BN+CM的最小值.
28.在平面直角坐标系xOy中,给出如下定义:点P是图形W外一点,点Q在PO的延长线上,使得,如果点Q在图形W上,则称点P是图形W的“延长2分点”.例如:如图1,A(2,4),B(2,2),是线段AB外一点,Q(2,3)在PO的延长线上,且,因为点Q在线段AB上,所以点P是线段AB的“延长2分点”.
(1)如图1,已知图形W1:线段AB,A(2,4),B(2,2),在,P2(﹣1,﹣1),P3(﹣1,﹣2)中, 是图形W1的“延长2分点”;
(2)如图2,已知图形W2:线段BC,B(2,2),C(5,2),若直线MN:y=﹣x+b上存在点P是图形W2的“延长2分点”,求b的最小值;
(3)如图3,已知图形W3:以T(t,1)为圆心,半径为1的⊙T,若以D(﹣1,﹣2),E(﹣1,1),F(2,1)为顶点的等腰直角三角形DEF上存在点P,使得点P是图形W3的“延长2分点”.请直接写出t的取值范围.
(
1
/
9
)
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.2024的绝对值是( )
A.﹣2024 B.2024 C. D.
2.若∠A=80°,则∠A的补角是( )
A.100° B.80° C.40° D.10°
3.2024年一季度,兰州市坚持稳中求进、综合施策,全市国民经济起步平稳,开局良好.一季度全市地区生产总值87790000000元,数据87790000000用科学记数法表示为( )
A.87.79×109 B.8.779×109
C.8.779×1010 D.8.779×1011
4.计算:2a(a﹣1)﹣2a2=( )
A.a B.﹣a C.2a D.﹣2a
5.一次函数y=2x﹣3的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.如图,小明在地图上量得∠1=∠2,由此判断幸福大街与平安大街互相平行,他判断的依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.对顶角相等
7.如图,小张想估测被池塘隔开的A,B两处景观之间的距离,他先在AB外取一点C,然后步测出AC,BC的中点D,E,并步测出DE的长约为18m,由此估测A,B之间的距离约为( )
A.18m B.24m C.36m D.54m
8.七巧板、九连环、华容道、鲁班锁是深受大家喜爱的益智玩具.现将1个七巧板,2个九连环,1个华容道,2个鲁班锁分别装在6个不透明的盒子中(每个盒子装1个),所有盒子除里面的玩具外均相同.从这6个盒子中随机抽取1个盒子,抽中七巧板的概率是( )
A. B. C. D.
9.关于x的一元二次方程9x2﹣6x+c=0有两个相等的实数根,则c=( )
A.﹣9 B.4 C.﹣1 D.1
10.数学家朱世杰所著的《四元玉鉴》是中国元代重要的数学著作之一,书中记载着这样一个问题,大意是:999文钱买了甜果和苦果共1000个,11文钱可买9个甜果,4文钱可买7个苦果,问甜果,苦果各买了多少个?设买了甜果x个,苦果y个,则可列方程组为( )
A.
B.
C.
D.
11.如图,在△ABC中,AB=AC,∠BAC=130°,DA⊥AC,则∠ADB=( )
A.100° B.115° C.130° D.145°
12.如图1,在菱形ABCD中,∠ABC=60°,连接BD,点M从B出发沿BD方向以的速度运动至D,同时点N从B出发沿BC方向以1cm/s的速度运动至C,设运动时间为x(s),△BMN的面积为y(cm2).y与x的函数图象如图2所示,则菱形ABCD的边长为( )
A. B. C.4cm D.8cm
二、填空题(本大题共4小题,每小题3分,共12分)
13.因式分解:a2﹣2a+1= .
14.如图,四边形ABCD为正方形.△ADE为等边三角形,EF⊥AB于点F,若AD=4,则EF= .
15.“轮动发石车”是我国古代的一种投石工具,在春秋战国时期被广泛应用,图1是陈列在展览馆的仿真模型.图2是模型驱动部分的示意图,其中⊙M,⊙N的半径分别是1cm和10cm,当⊙M顺时针转动3周时,⊙N上的点P随之旋转n°,则n= .
16.甲,乙两人在相同条件下各射击10次.两人的成绩(单位:环)如图所示.现有以下三个推断:
①甲的成绩更稳定;
②乙的平均成绩更高;
③每人再射击一次,乙的成绩一定比甲高.
其中正确的是 .(填序号)
三、解答题(本大题共12小题,共72分.解答时写出必要的文字说明、证明过程或演算步骤)
17.计算:.
18.解不等式组:.
19.先化简,再求值:,其中a=4.
20.如图,反比例函数与一次函数y=mx+1的图象交于点A(2,3),点B是反比例函数图象上一点,BC⊥x轴于点C,交一次函数的图象于点D,连接AB.(1)求反比例函数与一次函数y=mx+1的表达式;
(2)当OC=4时,求△ABD的面积.
21.如图,在△ABC中,AB=AC,D是BC的中点,CE∥AD,AE⊥AD,EF⊥AC.
(1)求证:四边形ADCE是矩形;
(2)若BC=4,CE=3,求EF的长.
22.在校园科技节期间,科普员为同学们进行了水火箭的发射表演,图1是某型号水火箭的实物图,水火箭发射后的运动路线可以看作是一条抛物线.为了解水火箭的相关性能,同学们进一步展开研究.如图2建立直角坐标系.水火箭发射后落在水平地面A处.科普员提供了该型号水火箭与地面成一定角度时,从发射到着陆过程中,水火箭距离地面OA的竖直高度y(m)与离发射点O的水平距离x(m)的几组关系数据如下:
水平距离x(m) 0 3 4 10 15 20 22 27
竖直高度y(m) 0 3.24 4.16 8 9 8 7.04 3.24
(1)根据如表,请确定抛物线的表达式;
(2)请计算当水火箭飞行至离发射点O的水平距离为5m时,水火箭距离地面的竖直高度.
23.观察发现:劳动人民在生产生活中创造了很多取材简单又便于操作的方法,正如木匠刘师傅的“木条画直角法”.如图1,他用木条能快速画出一个以点A为顶点的直角,具体作法如下:
①木条的两端分别记为点M,N,先将木条的端点M与点A重合,任意摆放木条后,另一个端点N的位置记为点B,连接AB;
②木条的端点N固定在点B处,将木条绕点B顺时针旋转一定的角度,端点M的落点记为点C(点A,B,C不在同一条直线上);
③连接CB并延长,将木条沿点C到点B的方向平移,使得端点M与点B重合,端点N在CB延长线上的落点记为点D;
④用另一根足够长的木条画线,连接AD,AC,则画出的∠DAC是直角.
操作体验:(1)根据“观察发现”中的信息重现刘师傅的画法.如图2,BA=BC.请画出以点A为顶点的直角,记作∠DAC;
推理论证:(2)如图1,小亮尝试揭示此操作的数学原理,请你补全括号里的证明依据:
证明:∵AB=BC=BD,
∴△ABC与△ABD是等腰三角形.
∴∠BCA=∠BAC,∠BDA=∠BAD.(依据1)
∴∠BCA+∠BDA=∠BAC+∠BAD=∠DAC.
∵∠DAC+∠BCA+∠BDA=180°,(依据2)
∴2∠DAC=180°.
∴∠DAC=90°.
依据1: :依据2: ;
拓展探究:(3)小亮进一步研究发现,用这种方法作直角存在一定的误差,用平时学习的尺规作图的方法可以减少误差.如图3,点O在直线l上,请用无刻度的直尺和圆规在图3中作出一个以O为顶点的直角,记作∠POQ,使得直角边OP(或OQ)在直线l上.(保留作图痕迹,不写作法)
24.为落实“双减”政策,培养德智体美劳全面发展的时代新人,某校组织调研学生体育和美育发展水平.现从七年级共180名学生中随机抽取20名学生,对每位学生的体育和美育水平进行测评后按百分制分数量化,并进行等级评定(成绩用x表示,分为四个等级,包括优秀:90≤x≤100;良好:80≤x<90;合格:70≤x<80;待提高:x<70).对数据进行整理,描述和分析,部分信息如下.
信息一:体育成绩的人数(频数)分布图如图.
信息二:美育成绩的人数(频数)分布表如下.
分组 90≤x≤100 80≤x<90 70≤x<80 x<70
人数 m 7 2 7
信息三:20位学生的体育成绩和美育成绩得分统计如下(共20个点).
根据以上信息,回答下列问题:
(1)填空:m= ;
(2)下列结论正确的是 ;(填序号)
①体育成绩低于80分的人数占抽取人数的40%;
②参与测评的20名学生美育成绩的中位数对应的等级是“合格”;
③在信息三中,相比于点A所代表的学生,点B所代表的学生的体育水平与其大致相同,但美育水平还存在一定差距,需要进一步提升;
(3)请结合以上信息,估计七年级全体学生中体育和美育两项成绩均属于“优秀”等级的人数.
25.单摆是一种能够产生往复摆动的装置.某兴趣小组利用摆球和摆线进行与单摆相关的实验探究,并撰写实验报告如下.
实验主题 探究摆球运动过程中高度的变化
实验用具 摆球,摆线,支架,摄像机等
实验说明 如图1,在支架的横杆点O处用摆线悬挂一个摆球,将摆球拉高后松手,摆球开始往复运动.(摆线的长度变化忽略不计) 如图2,摆球静止时的位置为点A,拉紧摆线将摆球拉至点B处,BD⊥OA.∠BOA=64°,BD=20.5cm;当摆球运动至点C时,∠COA=37°,CE⊥OA.(点O,A,B,C,D,E在同一平面内)
实验图示
解决问题:根据以上信息,求ED的长.(结果精确到0.1cm)
参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05.
26.如图,△ABC内接于⊙O,AB为⊙O的直径,点D为⊙O上一点,BC=BD,延长BA至E,使得∠ADE=∠CBA.
(1)求证:ED是⊙O的切线;
(2)若BO=4,,求ED的长.
27.综合与实践
【问题情境】在数学综合实践课上,同学们以特殊三角形为背景.探究动点运动的几何问题.如图,在△ABC中,点M,N分别为AB,AC上的动点(不含端点),且AN=BM.
【初步尝试】(1)如图1,当△ABC为等边三角形时,小颜发现:将MA绕点M逆时针旋转120°得到MD,连接BD,则MN=DB,请思考并证明;
【类比探究】(2)小梁尝试改变三角形的形状后进一步探究:如图2,在△ABC中,AB=AC,∠BAC=90°,AE⊥MN于点E,交BC于点F,将MA绕点M逆时针旋转90°得到MD,连接DA,DB.试猜想四边形AFBD的形状,并说明理由;
【拓展延伸】(3)孙老师提出新的探究方向:如图3,在△ABC中,AB=AC=4,∠BAC=90°,连接BN,CM,请直接写出BN+CM的最小值.
28.在平面直角坐标系xOy中,给出如下定义:点P是图形W外一点,点Q在PO的延长线上,使得,如果点Q在图形W上,则称点P是图形W的“延长2分点”.例如:如图1,A(2,4),B(2,2),是线段AB外一点,Q(2,3)在PO的延长线上,且,因为点Q在线段AB上,所以点P是线段AB的“延长2分点”.
(1)如图1,已知图形W1:线段AB,A(2,4),B(2,2),在,P2(﹣1,﹣1),P3(﹣1,﹣2)中, 是图形W1的“延长2分点”;
(2)如图2,已知图形W2:线段BC,B(2,2),C(5,2),若直线MN:y=﹣x+b上存在点P是图形W2的“延长2分点”,求b的最小值;
(3)如图3,已知图形W3:以T(t,1)为圆心,半径为1的⊙T,若以D(﹣1,﹣2),E(﹣1,1),F(2,1)为顶点的等腰直角三角形DEF上存在点P,使得点P是图形W3的“延长2分点”.请直接写出t的取值范围.
(
1
/
9
)
同课章节目录
