【中考冲刺】人教版2016年初中数学中考复习课件 专题3 抛物线下线段和三角形问题(共21张PPT)
文档属性
| 名称 | 【中考冲刺】人教版2016年初中数学中考复习课件 专题3 抛物线下线段和三角形问题(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 760.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-28 00:00:00 | ||
图片预览








文档简介
课件21张PPT。方法指导专题3 抛物线下线段和三角形问题真题回顾试题分析满分解答变式训练方法指导根据近几年的中考试卷,在所有的压轴题里面,以二次函数为载体,结合几何图形的题型是中考的热点和难点,解答此类试题需要用到的数学思想如下:
(1)函数思想;(2)数形结合思想;(3)转化思想;(4)分类讨论思想.
二次函数综合题,主要是以二次函数为主线,利用函数的图象与性质,结合二次函数的图象信息和点在函数图象上即点的坐标满足函数表达式等. :解题策略:应用函数思想解题,确立变量之间的函数表达式是关键步骤,主要分为下面四种情况:
(1)根据题意建立变量之间的函数表达式,把问题转化为相应的函数问题;
(2)用待定系数法求函数表达式;
(3)利用两个三角形相似解决最值问题;
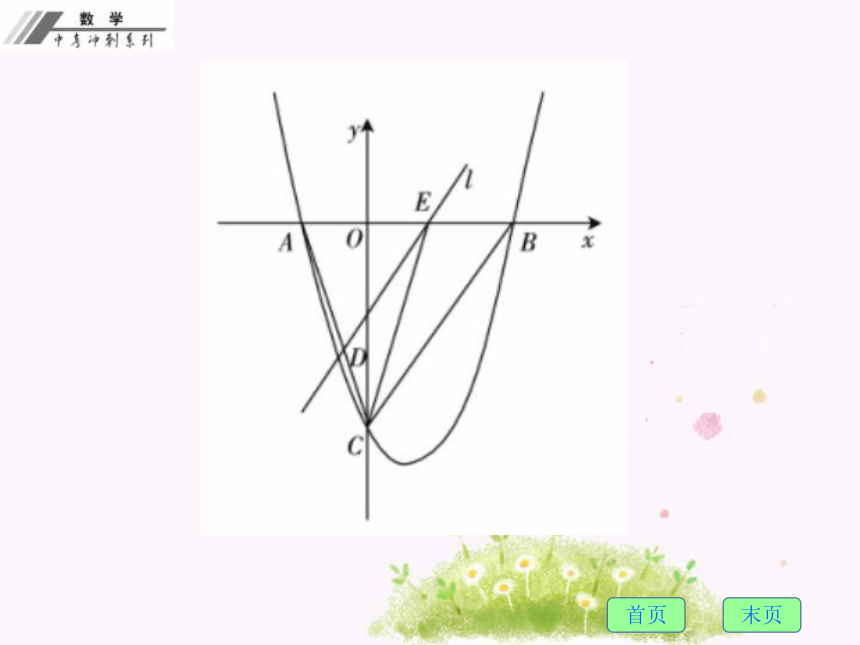
(4)动点与图形面积的关系,动点与线段之和最短问题的关系.真题回顾例 (2012?广东)如图-1,抛物线y=12x2-32x-9与x轴交于A,B两点,与y轴交于点C,连接BC,AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A,B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为S,求S关于m的函数表达式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
本题考查了学生对函数与其图象的认识及提取信息的能力,用到的知识点有二次函数的性质、相似三角形的性质、图形面积的求法等等,总体来说难度不高.具体可分析如下:
(1)已知抛物线的表达式,当x=0时,可确定点C的坐标;当y=0时,可确定点A,B的坐标,进而确定AB,OC的长;
(2)直线l∥BC,可得出△AED与△ABC相似,则它们的面积比等于相似比的平方.由此得到关于S,m的函数表达式;根据点E与点A,B不重合可确定m的取值范围;
试题分析(3)①首先用含m的式子表示出△AEC的面积,又△AEC,△AED的面积差即为△CDE的面积,由此可得关于S△CDE,m的函数表达式,然后根据函数的性质可得到S△CDE的最大面积以及此时m的值;②过点E作BC的垂线EM,这个垂线段的长即为与BC相切的⊙E的半径,可根据相似三角形△BEM,△BCO得到的相关比例线段求得该半径的值,由此得解.
满分解答变式训练1.(2015?黔东南州)如图-3,已知二次函数y1=-x2+134x+c的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过点A,B的直线为y2=kx+b.
(1)求二次函数y?1的表达式及点B的坐标;
(2)由图象写出满足y1<y2的自变量x的取值范围;
(3)在两坐标轴上是否存在点P,使得△ABP是以AB为底边的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
2.(2015?青海)如图-4,二次函数y=ax2+bx-3的图象与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,该抛物线的顶点为M.
(1)求该抛物线的表达式;
(2)判断△BCM的形状,并说明理由;
(3)探究坐标轴上是否存在点P,使得以点P,A,C为顶点的三角形与△BCM相似.若存在,请直接写出点P的坐标;若不存在,请说明理由.
谢谢!!
(1)函数思想;(2)数形结合思想;(3)转化思想;(4)分类讨论思想.
二次函数综合题,主要是以二次函数为主线,利用函数的图象与性质,结合二次函数的图象信息和点在函数图象上即点的坐标满足函数表达式等. :解题策略:应用函数思想解题,确立变量之间的函数表达式是关键步骤,主要分为下面四种情况:
(1)根据题意建立变量之间的函数表达式,把问题转化为相应的函数问题;
(2)用待定系数法求函数表达式;
(3)利用两个三角形相似解决最值问题;
(4)动点与图形面积的关系,动点与线段之和最短问题的关系.真题回顾例 (2012?广东)如图-1,抛物线y=12x2-32x-9与x轴交于A,B两点,与y轴交于点C,连接BC,AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A,B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为S,求S关于m的函数表达式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
本题考查了学生对函数与其图象的认识及提取信息的能力,用到的知识点有二次函数的性质、相似三角形的性质、图形面积的求法等等,总体来说难度不高.具体可分析如下:
(1)已知抛物线的表达式,当x=0时,可确定点C的坐标;当y=0时,可确定点A,B的坐标,进而确定AB,OC的长;
(2)直线l∥BC,可得出△AED与△ABC相似,则它们的面积比等于相似比的平方.由此得到关于S,m的函数表达式;根据点E与点A,B不重合可确定m的取值范围;
试题分析(3)①首先用含m的式子表示出△AEC的面积,又△AEC,△AED的面积差即为△CDE的面积,由此可得关于S△CDE,m的函数表达式,然后根据函数的性质可得到S△CDE的最大面积以及此时m的值;②过点E作BC的垂线EM,这个垂线段的长即为与BC相切的⊙E的半径,可根据相似三角形△BEM,△BCO得到的相关比例线段求得该半径的值,由此得解.
满分解答变式训练1.(2015?黔东南州)如图-3,已知二次函数y1=-x2+134x+c的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过点A,B的直线为y2=kx+b.
(1)求二次函数y?1的表达式及点B的坐标;
(2)由图象写出满足y1<y2的自变量x的取值范围;
(3)在两坐标轴上是否存在点P,使得△ABP是以AB为底边的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
2.(2015?青海)如图-4,二次函数y=ax2+bx-3的图象与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,该抛物线的顶点为M.
(1)求该抛物线的表达式;
(2)判断△BCM的形状,并说明理由;
(3)探究坐标轴上是否存在点P,使得以点P,A,C为顶点的三角形与△BCM相似.若存在,请直接写出点P的坐标;若不存在,请说明理由.
谢谢!!
同课章节目录
