【中考冲刺】人教版2016年初中数学中考复习课件专题6 几何动态问题(共23张PPT)
文档属性
| 名称 | 【中考冲刺】人教版2016年初中数学中考复习课件专题6 几何动态问题(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-28 14:08:41 | ||
图片预览







文档简介
课件23张PPT。方法指导专题6 几何动态问题真题回顾试题分析满分解答变式训练方法指导所谓“几何动态问题”是指题设图形中存在一个或多个动点,甚至是一个图形,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识,如平移、旋转、对称和运动过程中的面积变化关系等来解决问题.此类问题涉及的主要数学思想有:分类讨论思想、函数思想、方程思想、数形结合思想和转化思想.几何动态问题在中考中多是以动态几何为主线的压轴题的形式出现:第一种是点动问题;第二种是线动问题;第三种是面动问题. 解决几何动态问题的常见方法有:(1)从特殊问题探路,向一般问题推证;
(2)借助动手实践,通过具体操作确认;
(3)适当建立联系,通过计算进行说明.
真题回顾例 (2014?广东)如图-1,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB,AC,AD于点E,F,H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).
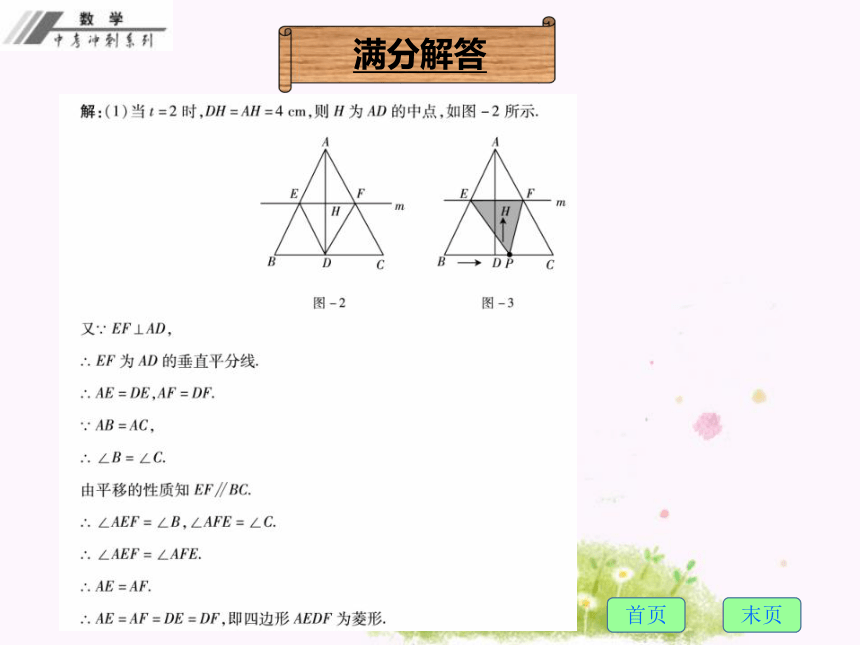
(1)当t=2时,连接DE,DF,求证:四边形AEDF为菱形;
(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;
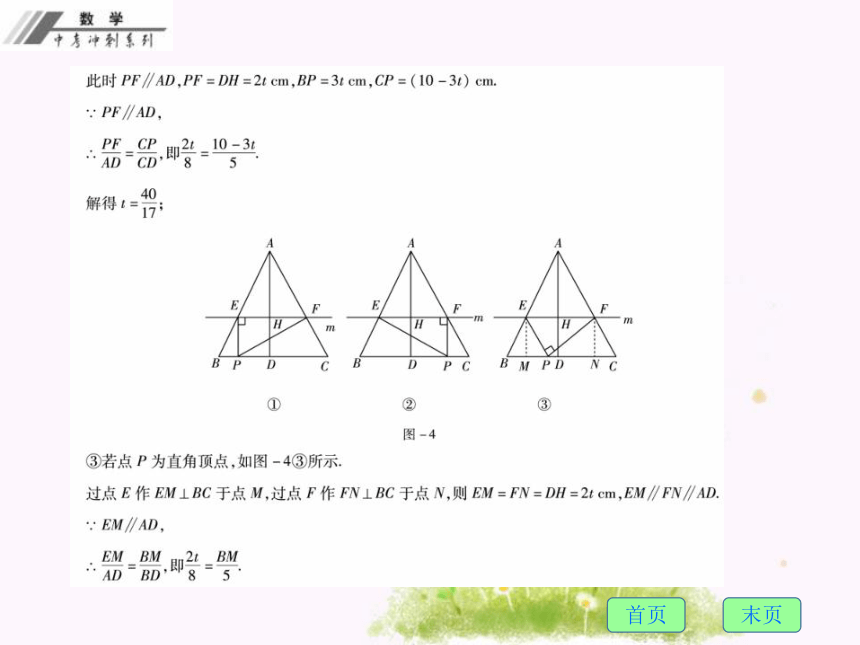
(3)是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.
试题分析(1)如图-2所示,利用菱形的定义证明;
(2)如图-3所示,首先求出△PEF的面积的表达式,然后利用二次函数的性质求解;
(3)如图-4所示,分三种情形,需要分类讨论,分别求解.满分解答变式训练1.(2015?吉林)两个三角板ABC,DEF按图-5所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点、线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时,停止运动.设三角板平移的距离为x,两个三角板重叠部分的面积为y.
(1)当点C落在边EF上时,x= ;
(2)求y关于x的函数表达式,并写出自变量x的取值范围;
(3)设BC的中点为M,DF的中点为N,直接写出在三角板平移过程中,点M与点N之间距离的最小值.
谢谢!!
(2)借助动手实践,通过具体操作确认;
(3)适当建立联系,通过计算进行说明.
真题回顾例 (2014?广东)如图-1,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB,AC,AD于点E,F,H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).
(1)当t=2时,连接DE,DF,求证:四边形AEDF为菱形;
(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;
(3)是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.
试题分析(1)如图-2所示,利用菱形的定义证明;
(2)如图-3所示,首先求出△PEF的面积的表达式,然后利用二次函数的性质求解;
(3)如图-4所示,分三种情形,需要分类讨论,分别求解.满分解答变式训练1.(2015?吉林)两个三角板ABC,DEF按图-5所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点、线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时,停止运动.设三角板平移的距离为x,两个三角板重叠部分的面积为y.
(1)当点C落在边EF上时,x= ;
(2)求y关于x的函数表达式,并写出自变量x的取值范围;
(3)设BC的中点为M,DF的中点为N,直接写出在三角板平移过程中,点M与点N之间距离的最小值.
谢谢!!
同课章节目录
