湘教版七年级下册(新)第4章《相交线与平行线》同步数学试卷(附答案)
文档属性
| 名称 | 湘教版七年级下册(新)第4章《相交线与平行线》同步数学试卷(附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 153.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-28 00:00:00 | ||
图片预览

文档简介
第4章 相交线与平行线
一、选择题
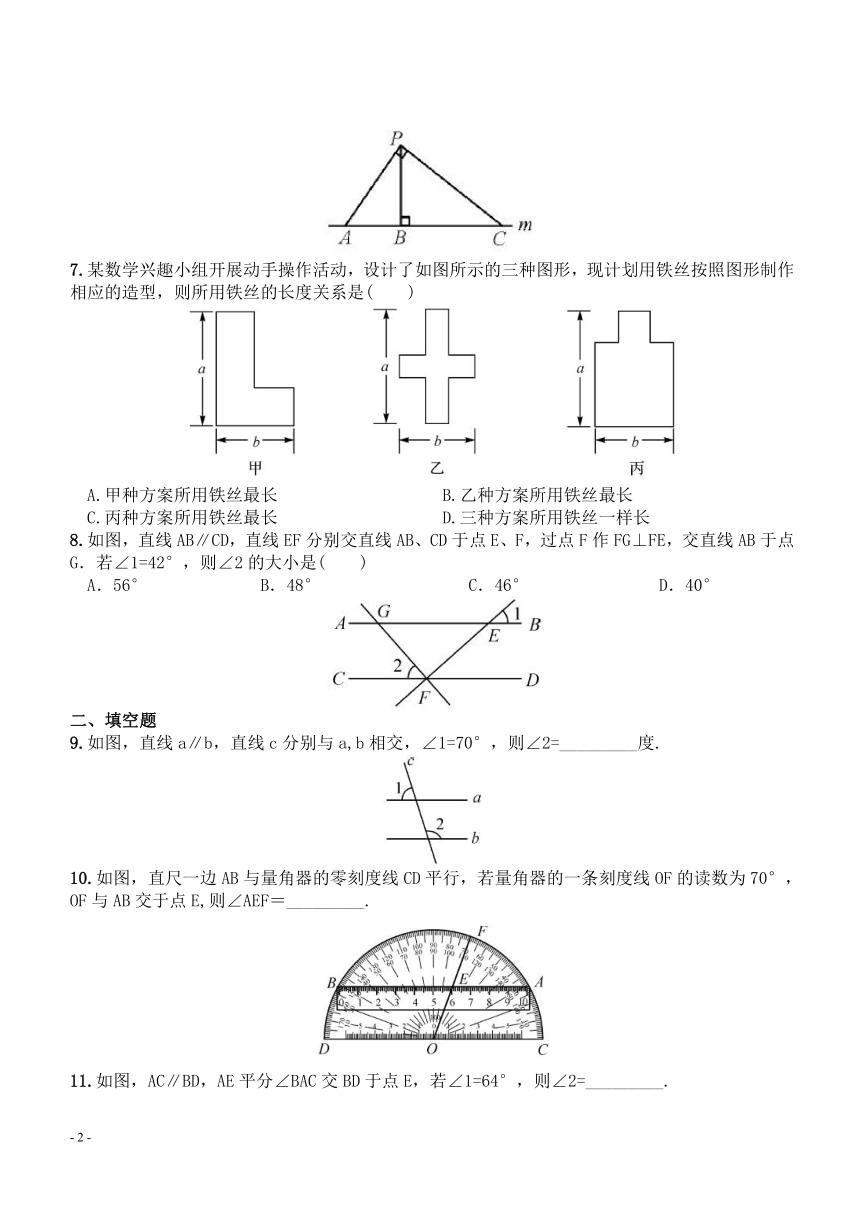
1.下列图形中,∠1与∠2是对顶角的是( )
2.下列说法正确的是( )
A.同位角相等 B.内错角相等 C.同旁内角相等,两直线平行 D.对顶角相等
3.如图,AB∥CD,AD∥BC,则下列各式不一定正确的是( )
A.∠1+∠2=180° B.∠2+∠3=180° C.∠3+∠4=180° D.∠2+∠4=180°
4.如图,∠1=40°,如果CD∥BE,那么∠B的度数为( )
A.160° B.140° C.60° D.50°
5.如图,下列条件中,不能判定直线a∥b的是( )
A.∠3=∠5 B.∠2=∠6 C.∠1=∠2 D.∠4+∠6=180°
6.如图所示,P为直线m外一点,点A,B,C在直线m上,且PB⊥m,垂足为B,∠APC=90°,则下列说法错误的是( )
A.线段PB的长度叫做点P到直线m的距离 B.PA,PB,PC三条线段中,PB最短
C.线段AC的长度等于点P到直线m的距离 D.线段PA的长度叫做点A到直线PC的距离
7.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
8.如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,过点F作FG⊥FE,交直线AB于点G.若∠1=42°,则∠2的大小是( )
A.56° B.48° C.46° D.40°
二、填空题
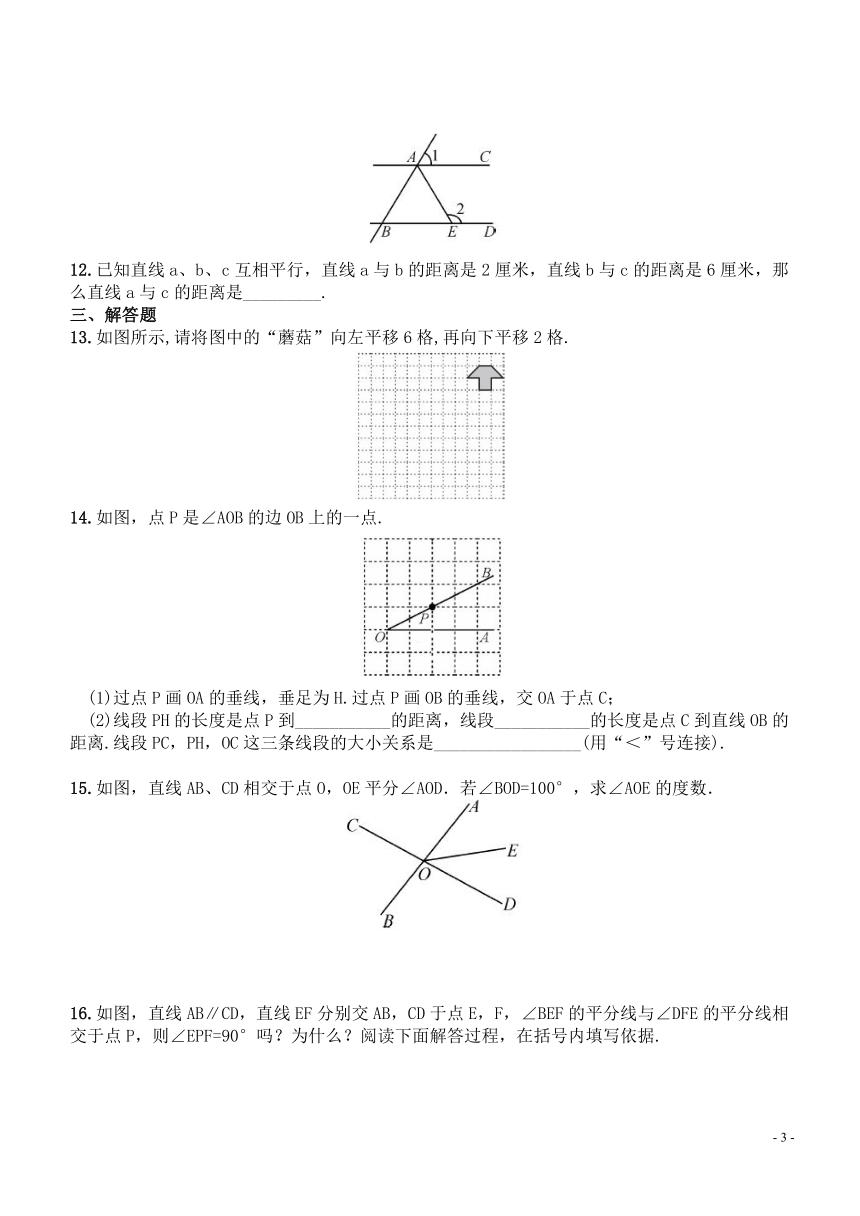
9.如图,直线a∥b,直线c分别与a,b相交,∠1=70°,则∠2=_________度.
10.如图,直尺一边AB与量角器的零刻度线CD平行,若量角器的一条刻度线OF的读数为70°,OF与AB交于点E,则∠AEF=_________.
11.如图,AC∥BD,AE平分∠BAC交BD于点E,若∠1=64°,则∠2=_________.
12.已知直线a、b、c互相平行,直线a与b的距离是2厘米,直线b与c的距离是6厘米,那么直线a与c的距离是_________.
三、解答题
13.如图所示,请将图中的“蘑菇”向左平移6格,再向下平移2格.
14.如图,点P是∠AOB的边OB上的一点.
(1)过点P画OA的垂线,垂足为H.过点P画OB的垂线,交OA于点C;
(2)线段PH的长度是点P到___________的距离,线段___________的长度是点C到直线OB的距离.线段PC,PH,OC这三条线段的大小关系是_________________(用“<”号连接).
15.如图,直线AB、CD相交于点O,OE平分∠AOD.若∠BOD=100°,求∠AOE的度数.
16.如图,直线AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P,则∠EPF=90°吗?为什么?阅读下面解答过程,在括号内填写依据.
解:∠EPF=90°.
理由:
过P作PG∥AB,因为AB∥CD(______________________),
所以AB∥PG∥CD(_________________________________).
所以∠1=∠2,∠3=∠4,∠BEF+∠EFD=180°(______________________).
又因为EP平分∠BEF,FP平分∠EFD(___________),
所以∠1=∠BEF,∠4=∠EFD(___________).
所以∠EPF=∠2+∠3=∠1+∠4=∠BEF+∠EFD=(∠BEF+∠EFD)=×180°=90°.
17.如图,EA⊥AD,FB⊥AD,∠E=∠F,问∠ECA=∠D吗?为什么?
18.同一平面内的两条直线有相交和平行两种位置关系.
(1)如图a,若AB∥CD,点P在AB,CD外部,试说明∠BPD=∠B-∠D;
(2)将点P移到AB,CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?请说明你的结论成立的理由.
参考答案
1.C 2.D 3.D 4.B 5.C 6.C 7.D 8.B
9.110 10.70° 11.122° 12.4厘米或8厘米
13.图略.
14.(1)图略.
(2)OA;CP;PH15.因为∠BOD=100°,∠BOD+∠AOD=180°,
所以∠AOD=80°,
因为OE平分∠AOD.
所以∠AOE=∠AOD=40°.
16.已知
两条直线都和第三条直线平行,那么这两条直线互相平行
两条直线平行,内错角相等,同旁内角互补
已知
角平分线的定义
17.∠ECA=∠D.
理由:因为EA⊥AD,FB⊥AD,
所以EA∥FB.
所以∠CHB=∠E.
又因为∠E=∠F,
所以∠CHB=∠F.
所以EC∥FD.
所以∠D=∠ECA.
18.(1)过P作PE∥AB,
所以∠B=∠BPE.
因为AB∥CD,
所以PE∥CD.
所以∠D=∠DPE.
因为∠BPD=∠BPE-∠DPE,
所以∠BPD=∠B-∠D.
(2)不成立,结论是∠BPD=∠B+∠D.
过P作PF∥AB,
所以∠B=∠BPF.
因为AB∥CD,
所以PF∥CD.
所以∠D=∠DPF.
因为∠BPD=∠BPF+∠DPF,
所以∠BPD=∠B+∠D.
- 2 -
- 1 -
一、选择题
1.下列图形中,∠1与∠2是对顶角的是( )
2.下列说法正确的是( )
A.同位角相等 B.内错角相等 C.同旁内角相等,两直线平行 D.对顶角相等
3.如图,AB∥CD,AD∥BC,则下列各式不一定正确的是( )
A.∠1+∠2=180° B.∠2+∠3=180° C.∠3+∠4=180° D.∠2+∠4=180°
4.如图,∠1=40°,如果CD∥BE,那么∠B的度数为( )
A.160° B.140° C.60° D.50°
5.如图,下列条件中,不能判定直线a∥b的是( )
A.∠3=∠5 B.∠2=∠6 C.∠1=∠2 D.∠4+∠6=180°
6.如图所示,P为直线m外一点,点A,B,C在直线m上,且PB⊥m,垂足为B,∠APC=90°,则下列说法错误的是( )
A.线段PB的长度叫做点P到直线m的距离 B.PA,PB,PC三条线段中,PB最短
C.线段AC的长度等于点P到直线m的距离 D.线段PA的长度叫做点A到直线PC的距离
7.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
8.如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,过点F作FG⊥FE,交直线AB于点G.若∠1=42°,则∠2的大小是( )
A.56° B.48° C.46° D.40°
二、填空题
9.如图,直线a∥b,直线c分别与a,b相交,∠1=70°,则∠2=_________度.
10.如图,直尺一边AB与量角器的零刻度线CD平行,若量角器的一条刻度线OF的读数为70°,OF与AB交于点E,则∠AEF=_________.
11.如图,AC∥BD,AE平分∠BAC交BD于点E,若∠1=64°,则∠2=_________.
12.已知直线a、b、c互相平行,直线a与b的距离是2厘米,直线b与c的距离是6厘米,那么直线a与c的距离是_________.
三、解答题
13.如图所示,请将图中的“蘑菇”向左平移6格,再向下平移2格.
14.如图,点P是∠AOB的边OB上的一点.
(1)过点P画OA的垂线,垂足为H.过点P画OB的垂线,交OA于点C;
(2)线段PH的长度是点P到___________的距离,线段___________的长度是点C到直线OB的距离.线段PC,PH,OC这三条线段的大小关系是_________________(用“<”号连接).
15.如图,直线AB、CD相交于点O,OE平分∠AOD.若∠BOD=100°,求∠AOE的度数.
16.如图,直线AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P,则∠EPF=90°吗?为什么?阅读下面解答过程,在括号内填写依据.
解:∠EPF=90°.
理由:
过P作PG∥AB,因为AB∥CD(______________________),
所以AB∥PG∥CD(_________________________________).
所以∠1=∠2,∠3=∠4,∠BEF+∠EFD=180°(______________________).
又因为EP平分∠BEF,FP平分∠EFD(___________),
所以∠1=∠BEF,∠4=∠EFD(___________).
所以∠EPF=∠2+∠3=∠1+∠4=∠BEF+∠EFD=(∠BEF+∠EFD)=×180°=90°.
17.如图,EA⊥AD,FB⊥AD,∠E=∠F,问∠ECA=∠D吗?为什么?
18.同一平面内的两条直线有相交和平行两种位置关系.
(1)如图a,若AB∥CD,点P在AB,CD外部,试说明∠BPD=∠B-∠D;
(2)将点P移到AB,CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?请说明你的结论成立的理由.
参考答案
1.C 2.D 3.D 4.B 5.C 6.C 7.D 8.B
9.110 10.70° 11.122° 12.4厘米或8厘米
13.图略.
14.(1)图略.
(2)OA;CP;PH
所以∠AOD=80°,
因为OE平分∠AOD.
所以∠AOE=∠AOD=40°.
16.已知
两条直线都和第三条直线平行,那么这两条直线互相平行
两条直线平行,内错角相等,同旁内角互补
已知
角平分线的定义
17.∠ECA=∠D.
理由:因为EA⊥AD,FB⊥AD,
所以EA∥FB.
所以∠CHB=∠E.
又因为∠E=∠F,
所以∠CHB=∠F.
所以EC∥FD.
所以∠D=∠ECA.
18.(1)过P作PE∥AB,
所以∠B=∠BPE.
因为AB∥CD,
所以PE∥CD.
所以∠D=∠DPE.
因为∠BPD=∠BPE-∠DPE,
所以∠BPD=∠B-∠D.
(2)不成立,结论是∠BPD=∠B+∠D.
过P作PF∥AB,
所以∠B=∠BPF.
因为AB∥CD,
所以PF∥CD.
所以∠D=∠DPF.
因为∠BPD=∠BPF+∠DPF,
所以∠BPD=∠B+∠D.
- 2 -
- 1 -
