第五章 平抛和类平抛运动 课件(共23张PPT)
文档属性
| 名称 | 第五章 平抛和类平抛运动 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-07-17 11:43:17 | ||
图片预览








文档简介
(共23张PPT)
平抛和类平抛运动
学习目标
1、通过对平抛、类平抛运动概念的理解,树立物体的运动观念
2、通过对平抛、类平抛运动规律的研究,掌握“化曲为直”的物理思想
3、通过实例分析,灵活运用平抛、类平抛运动的相关规律
4、通过理论知识与实际问题相结合,体会物理与生活的紧密联系,增强学习物理知识的动力
平抛运动的基本规律
一、知识回顾
1.研究方法:化曲为直
分解为水平方向的匀速直线运动和竖直方向的自由落体运动。
2.基本规律
(1)位移关系
平抛运动的基本规律
一、知识回顾
1.研究方法:化曲为直
分解为水平方向的匀速直线运动和竖直方向的自由落体运动。
2.基本规律
(2)速度关系
平抛运动的基本规律
一、知识回顾
3.结论和推论
(1)飞行时间
由t=知,时间取决于下落高度h,与初速度v0无关。
(2)水平射程
x=v0t=v0 ,即水平射程由初速度v0和下落高度h共同决定,与其他因素无关。
(3)落地速度
=,以θ表示落地速度与水平正方向间的夹角,
落地速度与初速度v0和下落高度h有关。
平抛运动的基本规律
一、知识回顾
(4)速度改变量
任意相等时间间隔Δt内的速度改变量Δv=gΔt是相同的,方向恒为竖直向下。
平抛运动的基本规律
一、知识回顾
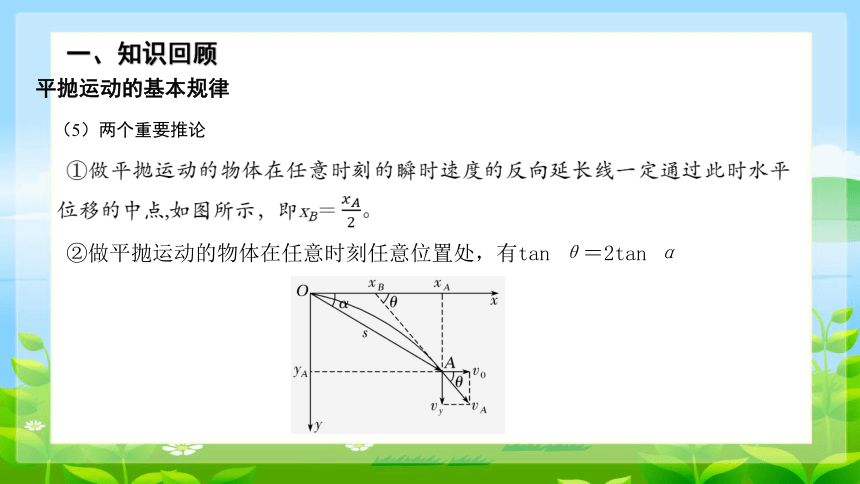
(5)两个重要推论
①做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图所示,即。
②做平抛运动的物体在任意时刻任意位置处,有tan θ=2tan α
二、学以致用
(一)平抛运动规律的应用
1.平抛运动的基本规律
[例1] 如图所示,在摩托车越野赛途中的水平路段前方有一个坑,该坑沿摩托车前进方向的水平宽度为3h,其左边缘a点比右边缘b点高0.5h.若摩托车经过a点时的动能为E1,它会落到坑内c点.c与a的水平距离和高度差均为h;若经过a点时的动能为E2,该摩托车恰能越过坑到达b点. 等于( )
A.20 B.18 C.9.0 D.3.0
解析 摩托车从a点做平抛运动到c点,
水平方向:h=v1t1,
竖直方向:h=gt12,
可解得v1=,动能E1=mv12=;
摩托车从a点做平抛运动到b点,水平方向:3h=v2t2,
竖直方向:0.5h=gt22,
解得v2=3,动能E2=mv22=mgh,故 =18,
答案:B
二、学以致用
二、学以致用
2.有约束条件的平抛运动
(1)“竖直墙壁”约束的平抛运动
[例2] (多选)从竖直墙的前方A处,沿AO方向水平发射三颗弹丸a、b、c,在墙上留下的弹痕如图所示,已知oa=ab=bc,则a、b、c三颗弹丸(不计空气阻力)( )
A.初速度大小之比是∶∶
B.初速度大小之比是1∶∶
C.从射出至打到墙上过程速度增量之比是1∶∶
D.从射出至打到墙上过程速度增量之比是∶∶
二、学以致用
解析 水平发射的弹丸做平抛运动,竖直方向上是自由落体运动,水平方向上是匀速直线运动
竖直方向上oa=ab=bc,即oa∶ob∶oc=1∶2∶3,
由h=gt2可知ta∶tb∶tc=1∶∶,
由水平方向x=v0t
可得va∶vb∶vc=1∶∶=∶∶,A正确,B错误;
由Δv=gt,可知从射出至打到墙上过程速度增量之比是1∶∶,
故C正确,D错误.
答案:AC
二、学以致用
2.有约束条件的平抛运动
(2)“斜面约束”的平抛运动
[例3] (多选) 如图所示,长木板OA的倾角θ=30°,在O点正上方的P处水平抛出一个小球,结果小球恰好垂直打在板面上距离O点为L的B点。重力加速度大小为g,空气阻力忽略不计。下列说法正确的是( )
A.小球在空中运动的时间为
B.小球被抛出时的初速度大小为
C.小球打到B点前瞬间的速度大小为
D.O、P两点间的距离为
二、学以致用
解析 小球在水平方向上的位移大小为x=Lcos 30°=L,
小球在B点的速度关系满足tan 60°=,又因为x=v0t,
联立解得v0=,t=,A错误,B正确;
由几何关系知,小球打在B点前的瞬时速度大小满足v==,C错误;
O、P两点间的距离为h=gt2+Lsin 30°=,D正确。
答案:BD
x
y
L
Vy
VB
V0
二、学以致用
2.有约束条件的平抛运动
(3)“曲面约束”的平抛运动
[例4] 如图所示,从O点以水平初速度v1、v2抛出两个小球(可视为质点),最终它们分别落在圆弧上的A点和B点,已知OA与OB互相垂直,且OA与竖直方向成α角,不计空气阻力,则两小球初速度之比v1∶v2为( )
A.tan α B.cos α C.tan α D.cos α
解析 设圆弧半径为R,两小球运动时间分别为t1、t2
对球1:Rsin α=v1t1,Rcos α=gt12
对球2:Rcos α=v2t2,Rsin α=gt22
联立可得=tan α , C正确。
C
二、学以致用
3.平抛中的临界、极值问题
[例5] 如图所示,容量足够大的圆筒竖直放置,水面高度为h,在圆筒侧壁开一个小孔P,筒内的水从小孔水平射出,设水到达地面时的落点距小孔的水平距离为x,小孔P到水面的距离为y。短时间内可认为筒内水位不变,重力加速度为g,不计空气阻力,在这段时间内下列说法正确的是( )
A.水从小孔P射出的速度大小为
B. y越小,则x越大
C. x与小孔的位置无关
D. 当y=时,x最大,最大值为h
二、学以致用
解析 取水面上质量为m的水滴,从小孔喷出时由机械能守恒定律有: mgy=mv2,解得v=,选项A错误;
水从小孔P射出时做平抛运动,则x=vt h-y=gt2
解得x=v=2可知x与小孔的位置有关,C错误
当y=h-y,即y=h时x最大,最大值为h,选项D正确,B错误。
答案:D
二、学以致用
(二)类平抛运动规律的应用
[例6] 如图所示,一个电子由静止开始经加速电场加速后,沿中心轴线从O点垂直射入偏转电场,并从另一侧射出打到荧光屏上的P点,O′点为荧光屏的中心。已知电子质量m=9.0×10-31 kg,电荷量e=1.6×10-19 C,加速电场电压U0=2 500 V,偏转电场电压U=200 V,极板的长度L1=6.0 cm,板间距离d=2.0 cm,极板的末端到荧光屏的距离L2=3.0 cm。(忽略电子所受重力,结果保留两位有效数字)求:
(1)电子射入偏转电场时的初速度v0的大小;
(2)电子打在荧光屏上的P点到O′点的距离h;
(3)电子经过偏转电场过程中电场力对它所做的功W。
二、学以致用
(1)电子射入偏转电场时的初速度v0的大小;
解析:(1)电子在加速电场中加速
根据动能定理有:eU0=mv02
解得:v0=
代入数据得:v0=3.0×107 m/s。
二、学以致用
(2)电子打在荧光屏上的P点到O′点的距离h;
(2)设电子在偏转电场中运动的时间为t,
电子射出偏转电场时在竖直方向上的侧位移为y
电子在水平方向做匀速直线运动:L1=v0t①
电子在竖直方向上做匀加速运动:y=t2②
根据牛顿第二定律有:=ma③
联立①②③代入数据得y=0.36 cm
由轨迹图知电子离开偏转电场时速度的反向延长线过偏转电场的中点
==
由几何关系有:
代值有h=0.72cm
二、学以致用
(3)电子经过偏转电场过程中电场力对它所做的功W。
(3)电子在偏转电场运动的过程中电场力对它做的功
W=eEy=ey=5.8×10-18 J。
三、拓展延伸
带电粒子在电场中的运动分析
四、点石成金
约束类平抛运动常见题型
运动情景 物理量分析
vy=gt,tan θ== → t=
x=v0t,y=gt2 → tan θ= → t=
tan θ== → t=
四、点石成金
约束类平抛运动常见题型
运动情景 物理量分析
落到斜面上时合速度与水平方向的夹角为φ,
tan φ====2tan θ ,α=φ-θ
tan θ== → t=
在半圆内的平抛运动,h=gt2,R+=v0t
平抛和类平抛运动
学习目标
1、通过对平抛、类平抛运动概念的理解,树立物体的运动观念
2、通过对平抛、类平抛运动规律的研究,掌握“化曲为直”的物理思想
3、通过实例分析,灵活运用平抛、类平抛运动的相关规律
4、通过理论知识与实际问题相结合,体会物理与生活的紧密联系,增强学习物理知识的动力
平抛运动的基本规律
一、知识回顾
1.研究方法:化曲为直
分解为水平方向的匀速直线运动和竖直方向的自由落体运动。
2.基本规律
(1)位移关系
平抛运动的基本规律
一、知识回顾
1.研究方法:化曲为直
分解为水平方向的匀速直线运动和竖直方向的自由落体运动。
2.基本规律
(2)速度关系
平抛运动的基本规律
一、知识回顾
3.结论和推论
(1)飞行时间
由t=知,时间取决于下落高度h,与初速度v0无关。
(2)水平射程
x=v0t=v0 ,即水平射程由初速度v0和下落高度h共同决定,与其他因素无关。
(3)落地速度
=,以θ表示落地速度与水平正方向间的夹角,
落地速度与初速度v0和下落高度h有关。
平抛运动的基本规律
一、知识回顾
(4)速度改变量
任意相等时间间隔Δt内的速度改变量Δv=gΔt是相同的,方向恒为竖直向下。
平抛运动的基本规律
一、知识回顾
(5)两个重要推论
①做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图所示,即。
②做平抛运动的物体在任意时刻任意位置处,有tan θ=2tan α
二、学以致用
(一)平抛运动规律的应用
1.平抛运动的基本规律
[例1] 如图所示,在摩托车越野赛途中的水平路段前方有一个坑,该坑沿摩托车前进方向的水平宽度为3h,其左边缘a点比右边缘b点高0.5h.若摩托车经过a点时的动能为E1,它会落到坑内c点.c与a的水平距离和高度差均为h;若经过a点时的动能为E2,该摩托车恰能越过坑到达b点. 等于( )
A.20 B.18 C.9.0 D.3.0
解析 摩托车从a点做平抛运动到c点,
水平方向:h=v1t1,
竖直方向:h=gt12,
可解得v1=,动能E1=mv12=;
摩托车从a点做平抛运动到b点,水平方向:3h=v2t2,
竖直方向:0.5h=gt22,
解得v2=3,动能E2=mv22=mgh,故 =18,
答案:B
二、学以致用
二、学以致用
2.有约束条件的平抛运动
(1)“竖直墙壁”约束的平抛运动
[例2] (多选)从竖直墙的前方A处,沿AO方向水平发射三颗弹丸a、b、c,在墙上留下的弹痕如图所示,已知oa=ab=bc,则a、b、c三颗弹丸(不计空气阻力)( )
A.初速度大小之比是∶∶
B.初速度大小之比是1∶∶
C.从射出至打到墙上过程速度增量之比是1∶∶
D.从射出至打到墙上过程速度增量之比是∶∶
二、学以致用
解析 水平发射的弹丸做平抛运动,竖直方向上是自由落体运动,水平方向上是匀速直线运动
竖直方向上oa=ab=bc,即oa∶ob∶oc=1∶2∶3,
由h=gt2可知ta∶tb∶tc=1∶∶,
由水平方向x=v0t
可得va∶vb∶vc=1∶∶=∶∶,A正确,B错误;
由Δv=gt,可知从射出至打到墙上过程速度增量之比是1∶∶,
故C正确,D错误.
答案:AC
二、学以致用
2.有约束条件的平抛运动
(2)“斜面约束”的平抛运动
[例3] (多选) 如图所示,长木板OA的倾角θ=30°,在O点正上方的P处水平抛出一个小球,结果小球恰好垂直打在板面上距离O点为L的B点。重力加速度大小为g,空气阻力忽略不计。下列说法正确的是( )
A.小球在空中运动的时间为
B.小球被抛出时的初速度大小为
C.小球打到B点前瞬间的速度大小为
D.O、P两点间的距离为
二、学以致用
解析 小球在水平方向上的位移大小为x=Lcos 30°=L,
小球在B点的速度关系满足tan 60°=,又因为x=v0t,
联立解得v0=,t=,A错误,B正确;
由几何关系知,小球打在B点前的瞬时速度大小满足v==,C错误;
O、P两点间的距离为h=gt2+Lsin 30°=,D正确。
答案:BD
x
y
L
Vy
VB
V0
二、学以致用
2.有约束条件的平抛运动
(3)“曲面约束”的平抛运动
[例4] 如图所示,从O点以水平初速度v1、v2抛出两个小球(可视为质点),最终它们分别落在圆弧上的A点和B点,已知OA与OB互相垂直,且OA与竖直方向成α角,不计空气阻力,则两小球初速度之比v1∶v2为( )
A.tan α B.cos α C.tan α D.cos α
解析 设圆弧半径为R,两小球运动时间分别为t1、t2
对球1:Rsin α=v1t1,Rcos α=gt12
对球2:Rcos α=v2t2,Rsin α=gt22
联立可得=tan α , C正确。
C
二、学以致用
3.平抛中的临界、极值问题
[例5] 如图所示,容量足够大的圆筒竖直放置,水面高度为h,在圆筒侧壁开一个小孔P,筒内的水从小孔水平射出,设水到达地面时的落点距小孔的水平距离为x,小孔P到水面的距离为y。短时间内可认为筒内水位不变,重力加速度为g,不计空气阻力,在这段时间内下列说法正确的是( )
A.水从小孔P射出的速度大小为
B. y越小,则x越大
C. x与小孔的位置无关
D. 当y=时,x最大,最大值为h
二、学以致用
解析 取水面上质量为m的水滴,从小孔喷出时由机械能守恒定律有: mgy=mv2,解得v=,选项A错误;
水从小孔P射出时做平抛运动,则x=vt h-y=gt2
解得x=v=2可知x与小孔的位置有关,C错误
当y=h-y,即y=h时x最大,最大值为h,选项D正确,B错误。
答案:D
二、学以致用
(二)类平抛运动规律的应用
[例6] 如图所示,一个电子由静止开始经加速电场加速后,沿中心轴线从O点垂直射入偏转电场,并从另一侧射出打到荧光屏上的P点,O′点为荧光屏的中心。已知电子质量m=9.0×10-31 kg,电荷量e=1.6×10-19 C,加速电场电压U0=2 500 V,偏转电场电压U=200 V,极板的长度L1=6.0 cm,板间距离d=2.0 cm,极板的末端到荧光屏的距离L2=3.0 cm。(忽略电子所受重力,结果保留两位有效数字)求:
(1)电子射入偏转电场时的初速度v0的大小;
(2)电子打在荧光屏上的P点到O′点的距离h;
(3)电子经过偏转电场过程中电场力对它所做的功W。
二、学以致用
(1)电子射入偏转电场时的初速度v0的大小;
解析:(1)电子在加速电场中加速
根据动能定理有:eU0=mv02
解得:v0=
代入数据得:v0=3.0×107 m/s。
二、学以致用
(2)电子打在荧光屏上的P点到O′点的距离h;
(2)设电子在偏转电场中运动的时间为t,
电子射出偏转电场时在竖直方向上的侧位移为y
电子在水平方向做匀速直线运动:L1=v0t①
电子在竖直方向上做匀加速运动:y=t2②
根据牛顿第二定律有:=ma③
联立①②③代入数据得y=0.36 cm
由轨迹图知电子离开偏转电场时速度的反向延长线过偏转电场的中点
==
由几何关系有:
代值有h=0.72cm
二、学以致用
(3)电子经过偏转电场过程中电场力对它所做的功W。
(3)电子在偏转电场运动的过程中电场力对它做的功
W=eEy=ey=5.8×10-18 J。
三、拓展延伸
带电粒子在电场中的运动分析
四、点石成金
约束类平抛运动常见题型
运动情景 物理量分析
vy=gt,tan θ== → t=
x=v0t,y=gt2 → tan θ= → t=
tan θ== → t=
四、点石成金
约束类平抛运动常见题型
运动情景 物理量分析
落到斜面上时合速度与水平方向的夹角为φ,
tan φ====2tan θ ,α=φ-θ
tan θ== → t=
在半圆内的平抛运动,h=gt2,R+=v0t
