(暑假自学课)第五单元圆检测卷-数学六年级上册人教版(含答案)
文档属性
| 名称 | (暑假自学课)第五单元圆检测卷-数学六年级上册人教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 745.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-18 22:02:36 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
(暑假自学课)第五单元圆检测卷-数学六年级上册人教版
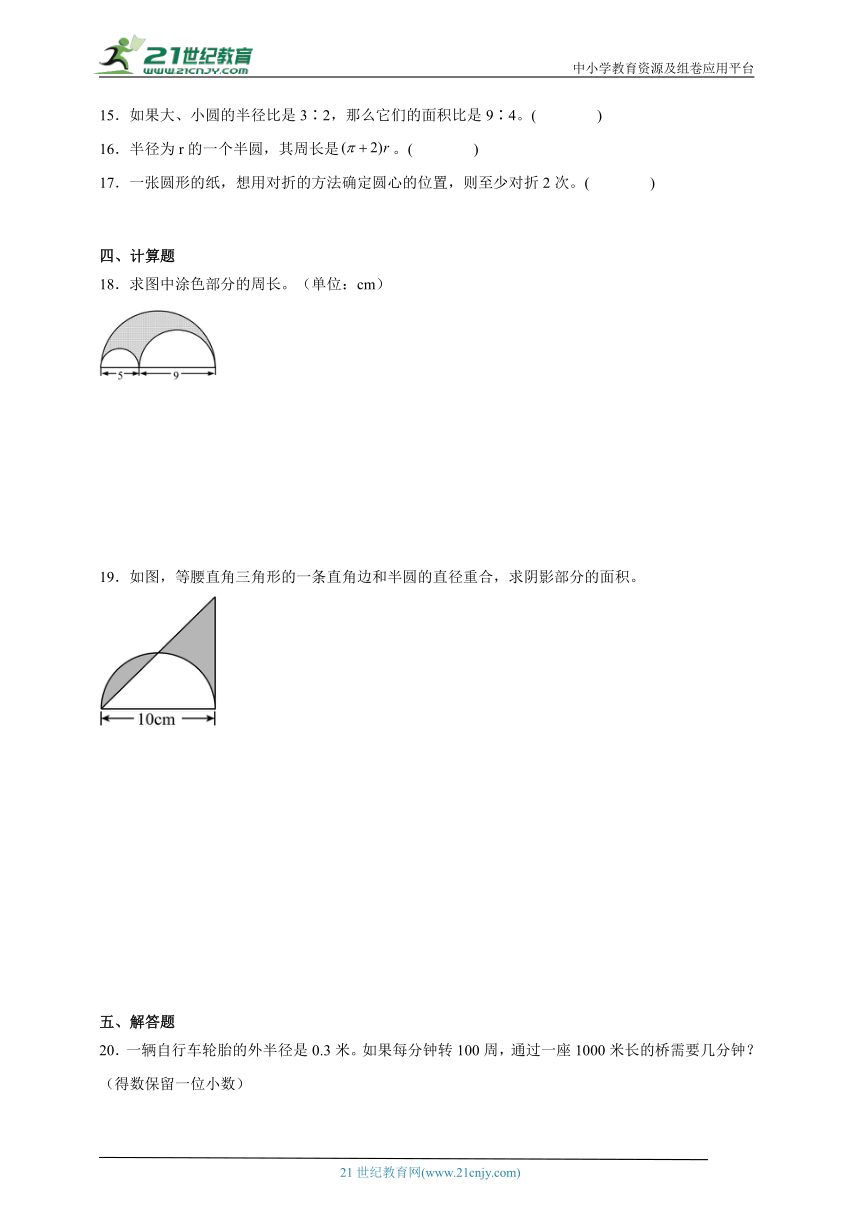
一、选择题
1.有( )条对称轴。
A.2 B.4 C.5 D.无数
2.分别以长方形、梯形的四个顶点为圆心,画半径为1cm的圆(如图)。比较两个图形涂色部分的面积,( )。
A.长方体的大 B.梯形的大 C.一样大 D.无法比较
3.一个圆形喷水池,半径是6米,水池外围有一条2米的环形小路,这条小路的面积是( )平方米。
A.4 B.36 C.64 D.28
4.把一个直径是10厘米的圆分成若干等份,然后把它剪开,照下图的样子拼起来,拼成的图形的周长比原来圆的周长增加( )厘米。
A.5 B.10 C.31.4 D.6.28
5.小红要剪一个面积是12.56平方厘米的圆形做笑脸。如果选择一张正方形硬纸片,那么这张正方形纸片的边长至少是( )厘米。
A.2 B.4 C.8 D.12.56
6.下面三个情境中,两个量之比可以用5∶4表示的是( )。
A.只有①② B.只有②③ C.只有①③ D.有①②③
二、填空题
7.智慧老人家圆形羊栏半径是10米,至少要用( )米的铁丝才能把羊栏围上5圈。
8.小圆的半径是4米,大圆的半径是6米,大圆和小圆周长的最简整数比是( ),大圆和小圆面积的最简整数比是( )。
9.街心公园有一个半圆形的花坛,花坛的直径是6m,这个半圆形的花坛的周长是( )m,面积是( )m2。
10.下图中正方形的面积是40cm2,圆的面积是( )cm2。
11.把一个由草绳编织成的圆形茶杯垫沿直径剪开,得到两个近似的三角形,再拼成平行四边形(如图所示),在剪拼的过程中面积保持不变,这个平行四边形的面积是( )cm2。
12.“外方内圆”与“外圆内方”是我国古代建筑常见的设计,如图中外面正方形的面积是,则内圆的面积是( ),如果外圆的面积是,则圆内正方形的面积是( )。
三、判断题
13.任何圆的周长都是直径的3.14倍。( )
14.下水道井盖平面轮廓做成圆形的,圆形井盖怎么放都不会掉到井里,并且能恰好盖住井口,是利用了同一圆中直径都相等的性质。( )
15.如果大、小圆的半径比是3∶2,那么它们的面积比是9∶4。( )
16.半径为r的一个半圆,其周长是。( )
17.一张圆形的纸,想用对折的方法确定圆心的位置,则至少对折2次。( )
四、计算题
18.求图中涂色部分的周长。(单位:cm)
19.如图,等腰直角三角形的一条直角边和半圆的直径重合,求阴影部分的面积。
五、解答题
20.一辆自行车轮胎的外半径是0.3米。如果每分钟转100周,通过一座1000米长的桥需要几分钟?(得数保留一位小数)
21.为了丰富学生的课后延时活动,手工社团的同学用一根铁丝围成一个长10厘米,宽5.7厘米的长方形,又用这根铁丝围成了一个最大的圆形,这个圆形的面积是多少?
22.李叔叔计划在边长8米的正方形天台上用油漆涂出一个最大的圆用于布置,若每平方米需要用油漆0.5千克,需要多少千克油漆?
23.如下图中的圆从点A开始,沿着直尺(单位:cm)向右滚动一周,到达点B。
(1)点B大约在哪里?请在图中的直尺上标出来。
(2)这个圆的面积是( )平方厘米。
24.社团制作木质三角形轨道:一个半径1cm的圆从B点出发,沿着边长6厘米的等边三角形的外壁滚动(无滑动),最后回到原来的位置。圆心经过的路程是多少厘米?(取3)
参考答案:
1.B
【分析】沿着一条直线将图形对折,两边的图形能够完全重合,这个图形叫做轴对称图形,这条直线是图形的对称轴,据此解答即可。
【详解】圆的对称轴有无数条,圆的对称轴是圆的直径所在直线,正方形有4条对称轴,这4条对称轴都是圆的直径所在直线,所以这个组合图形有4条对称轴。
故答案为:B
【点睛】本题考查对称轴、圆,解答本题的关键是掌握对称轴的概念。
2.C
【分析】需要分别求出长方形和梯形中阴影部分的扇形组成的图形的面积,长方形中四个四分之一圆的半径相等就能拼成一个整圆,根据圆的面积公式=π×半径2,即可求出长方形中圆的面积,梯形中阴影部分的扇形就能拼成一个整圆,面积同样为根据圆的面积公式=π×半径2,即可求出梯形中圆的面积,然后两者比较大小即可。
【详解】长方形中圆的面积:
S=π×半径2
=3.14×12
=3.14×1
=3.14(平方厘米)
梯形中圆的面积:
S=π×半径2
=3.14×12
=3.14×1
=3.14(平方厘米)
3.14=3.14,长方形中圆的面积和梯形中圆的面积一样大。
故答案为:C
3.D
【分析】这条小路的面积也就是圆环的面积,圆环的面积=大圆的面积-小圆的面积;根据圆的面积=πr2,大圆的半径是(6+2)米,小圆的半径是6米,代入相应数值计算,据此解答。
【详解】π×(6+2)2-π×62
=π×82-π×62
=π×(82-62)
=π×(64-36)
=28π(平方米)
因此这条小路的面积是(28π)平方米。
故答案为:D
4.B
【分析】把一个圆剪拼成一个近似的长方形,长方形的长等于圆的周长的一半,宽等于圆的半径;拼成的长方形的周长比原来圆的周长增加了2条宽的长度,即增加了2个半径的长度,据此解答。
【详解】10÷2×2=10(厘米)
拼成的图形的周长比原来圆的周长增加10厘米。
故答案为:B
5.B
【分析】由题意可知:正方形里剪一个最大的圆,圆的直径等于正方形边长时正方形最小,用圆的面积÷π,求出半径的平方,确定半径,求出直径,即正方形边长。
【详解】12.56÷3.14=4(平方厘米)
4=2×2
2×2=4(厘米)
所以正方形边长至少为4厘米。
故答案为:B
6.A
【分析】根据比的意义,写出各选项中两个量的比,再化简比,找出两个量的比可以用5∶4表示的选项即可。
【详解】①150∶120
=(150÷30)∶(120÷30)
=5∶4
哥哥与妹妹的身高之比是5∶4;
②橡皮的总价与数量之比是5∶4;
③(π×52)∶(π×42)
=25π∶16π
=25∶16
大圆与小圆的面积之比是25∶16,不能用5∶4表示;
故答案为:A
7.314
【分析】将数据代入圆的周长公式:C=2πr求出圆形羊栏的周长,再乘5即可。
【详解】3.14×2×10×5
=6.28×10×5
=62.8×5
=314(米)
至少要用314米的铁丝才能把羊栏围上5圈。
8. 3∶2 9∶4
【分析】将数据代入圆的周长公式:C=2πr及圆的面积公式S=πr2,分别求出大、小圆的周长,面积,写出周长比、面积比后化简即可。
【详解】小圆周长:π×2×4=8π(米)
小圆面积:π×42=16π(米)
大圆周长:π×2×6=12π(平方米)
大圆面积:π×62=36π(平方米)
大圆周长∶小圆周长=12π米∶8π米=3∶2
大圆面积∶小圆面积=36π平方米∶16π平方米=9∶4
小圆的半径是4米,大圆的半径是6米,大圆和小圆的周长比是3∶2,大圆和小圆的面积比是9∶4。
9. 15.42 14.13
【分析】由题意知:半圆的周长是圆周长一半加一条直径,半圆的面积是圆面积的一半。利用圆的周长计算公式,圆的面积计算公式,将数值代入计算即可。据此解答。
【详解】3.14×6÷2+6
=18.84÷2+6
=9.42+6
=15.42(米)
6÷2=3(米)
=28.26÷2
=14.13(平方米)
这个半圆形的花坛的周长是(15.42)m,面积是(14.13)m2。
【点睛】灵活运用圆的周长和面积计算公式是解答的关键。
10.125.6
【分析】从图中可知,正方形的边长等于圆的半径,根据正方形的面积公式S=a2可知,正方形的面积正好是r2,即r2=40,把r2的值代入圆的面积公式S=πr2中计算,即可求出圆的面积。
【详解】3.14×40=125.6(cm2)
圆的面积是125.6 cm2。
11.78.5
【分析】由图可知,平行四边形的高等于圆的半径,底等于圆周长的一半;根据圆的周长公式:C=2πr可得r=C÷2π,代入数据求出半径(也就是平行四边形的高),再代入平行四边形的面积公式:S=ah计算即可。
【详解】15.7×2÷2÷3.14
=31.4÷2÷3.14
=15.7÷3.14
=5(cm)
15.7×5=78.5(cm2)
这个平行四边形的面积是78.5cm2。
12. 12.56 18
【分析】根据正方形面积公式:面积=边长×边长;正方形面积是16dm2,4×4=16,所以正方形边长是4dm;正方形内最大的圆,圆的直径等于正方形的边长;圆的直径等于4dm;根据圆的面积公式:面积=π×半径2,代入数据,求出内圆的面积;
根据圆的面积公式:面积=π×半径2,半径2=面积÷π;用9π÷π=9,求出半径的平方;3×3=9,所以外圆的半径是3dm;圆内正方形的面积=直径×半径,据此求出圆内正方形的面积。
【详解】4×4=16;正方形的边长是4dm;
园内面积:3.14×(4÷2)2
=3.14×22
=3.14×4
=12.56(dm2)
9π÷π=9
3×3=9;外圆的半径是3dm。
3×2×3
=6×3
=18(dm2)
“外方内圆”与“外圆内方”是我国古代建筑常见的设计,外面正方形的面积16dm2,则内圆的面积是12.56dm2,如果外圆的面积是9πdm2,则圆内正方形的面积是18dm2。
13.×
【分析】根据教材中关于圆周率的含义的推导可知,圆的周长和它直径的比值,叫做圆周率,圆周率用“π”表示,π的取值是3.14159265…;由此判断即可。
【详解】一个圆的周长总是直径的π倍,π约等于3.14,并不等于3.14,原题说法错误。
故答案为:×
【点睛】此题的关键在于区分π和3.14的区别。
14.√
【分析】同圆或等圆中,所有的直径都相等,因此这就是圆形井盖设计成圆形的原因。
【详解】下水道井盖平面轮廓做成圆形的,圆形井盖怎么放都不会掉到井里,并且能恰好盖住井口,是利用了同一圆中直径都相等的性质,说法正确。
故答案为:√
【点睛】关键是熟悉圆的特征,根据圆的特征进行分析。
15.√
【分析】由题意可知,大、小圆的半径比是3∶2,则假设大、小圆的半径为3和2,再根据圆的面积公式:S=πr2,据此求出大、小圆的面积,进而求出它们的面积比。
【详解】假设大、小圆的半径为3和2
32π∶22π
=9π∶4π
=(9π÷π)∶(4π÷π)
=9∶4
则它们的面积比是9∶4。原题说法正确。
故答案为:√
【点睛】本题考查比的应用,结合圆的面积的计算方法是解题的关键。
16.√
【分析】根据圆的周长公式可计算出圆的周长,那么半圆的周长是圆周长的一半加上一条直径,由此解答即可。
【详解】半圆的周长:
=
=
故答案为:√
【点睛】此题考查的是圆的周长公式的灵活运用,要认真审题。
17.√
【分析】圆中心的那个点即圆心,所有直径都相交于圆心,将一个圆形纸片最少要对折两次,才能找到两条折痕相交的那个点,即圆心。
【详解】由分析可得:一张圆形的纸,想用对折的方法确定圆心的位置,则至少对折2次,原题说法正确。
故答案为:√
【点睛】本题考查了确定圆心的方法。
18.43.96cm
【分析】观察图形可知,涂色部分的周长=直径为(5+9)cm圆周长的一半+直径为9cm圆周长的一半+直径为5cm圆周长的一半,根据圆的周长公式C=πd,代入数据计算求解。
【详解】3.14×(5+9)÷2+3.14×9÷2+3.14×5÷2
=3.14×14÷2+3.14×9÷2+3.14×5÷2
=21.98+14.13+7.85
=43.96(cm)
涂色部分的周长是43.96cm。
19.25平方厘米
【分析】
如上图,添加两道红色辅助线,将A处阴影面积割补到B处后,阴影面积是一个底为10厘米,高为5厘米的等腰三角形面积。据此三角形面积=底×高÷2,将数值代入计算即可。
【详解】10×5÷2
=50÷2
=25(平方厘米)
阴影部分的面积是25平方厘米。
【点睛】根据等腰三角形特征,利用割补法,将不规则的阴影面积转换为规则图形的面积是解答的关键。
20.5.3分钟
【分析】先根据圆的周长公式C=2πr,求出自行车车轮转一周行驶的距离,再乘100周,即可求出自行车每分钟行驶的距离;然后用桥的长度除以自行车每分钟行驶的距离,求出自行车通过这座桥所需的时间。
【详解】2×3.14×0.3×100
=6.28×0.3×100
=1.884×100
=188.4(米)
1000÷188.4≈5.3(分钟)
答:通过一座1000米长的桥需要5.3分钟。
21.78.5平方厘米
【分析】根据长方形的周长=(长+宽)×2,求出这根铁丝的长度,再根据圆的周长=2×π×半径,可得半径=圆的周长÷π÷2,最后根据圆的面积=πr ,求出这个圆的面积。
【详解】(10+5.7)×2
=15.7×2
=31.4(厘米)
31.4÷3.14÷2
=10÷2
=5(厘米)
52×3.14
=25×3.14
=78.5(平方厘米)
答:这个圆形的面积是78.5平方厘米。
22.25.12千克
【分析】根据题意可知,圆的直径等于正方形的边长;根据圆的面积公式:面积=π×半径2,代入数据,求出圆的面积,再乘0.5,即求出需要油漆的重量。
【详解】3.14×(8÷2)2×0.5
=3.14×42×0.5
=3.14×16×0.5
=50.24×0.5
=25.12(千克)
答:需要25.12千克油漆。
23.(1)见详解
(2)3.14
【分析】(1)看图可知,圆的直径=3-1=2(厘米),根据圆的周长=πd,求出圆滚动一周的长度,确定B点位置即可;
(2)根据圆的面积公式:面积=πr2,代入数据,即可解答。
【详解】(1)3-1=2(厘米)
3.14×2=6.28(厘米)
2+6.28=8.28(厘米)
如图:
(2)3.14×(2÷2)2
=3.14×12
=3.14×1
=3.14(平方厘米)
圆的面积是3.14平方厘米。
24.24厘米
【分析】
圆心经过的路线如图,改路线由3条6厘米的线段与3条半径是1厘米,圆心角是(360°-90°×2-60°)的扇形的弧组成,这3条扇形的弧长总和恰好是1个半径1厘米的圆的周长,圆的周长=2×圆周率×半径,据此列式解答。
【详解】6×3+2×3×1
=18+6
=24(厘米)
答:圆心经过的路程是24厘米。
【点睛】关键是弄清楚圆心经过的路线,掌握并灵活运用圆的周长公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
(暑假自学课)第五单元圆检测卷-数学六年级上册人教版
一、选择题
1.有( )条对称轴。
A.2 B.4 C.5 D.无数
2.分别以长方形、梯形的四个顶点为圆心,画半径为1cm的圆(如图)。比较两个图形涂色部分的面积,( )。
A.长方体的大 B.梯形的大 C.一样大 D.无法比较
3.一个圆形喷水池,半径是6米,水池外围有一条2米的环形小路,这条小路的面积是( )平方米。
A.4 B.36 C.64 D.28
4.把一个直径是10厘米的圆分成若干等份,然后把它剪开,照下图的样子拼起来,拼成的图形的周长比原来圆的周长增加( )厘米。
A.5 B.10 C.31.4 D.6.28
5.小红要剪一个面积是12.56平方厘米的圆形做笑脸。如果选择一张正方形硬纸片,那么这张正方形纸片的边长至少是( )厘米。
A.2 B.4 C.8 D.12.56
6.下面三个情境中,两个量之比可以用5∶4表示的是( )。
A.只有①② B.只有②③ C.只有①③ D.有①②③
二、填空题
7.智慧老人家圆形羊栏半径是10米,至少要用( )米的铁丝才能把羊栏围上5圈。
8.小圆的半径是4米,大圆的半径是6米,大圆和小圆周长的最简整数比是( ),大圆和小圆面积的最简整数比是( )。
9.街心公园有一个半圆形的花坛,花坛的直径是6m,这个半圆形的花坛的周长是( )m,面积是( )m2。
10.下图中正方形的面积是40cm2,圆的面积是( )cm2。
11.把一个由草绳编织成的圆形茶杯垫沿直径剪开,得到两个近似的三角形,再拼成平行四边形(如图所示),在剪拼的过程中面积保持不变,这个平行四边形的面积是( )cm2。
12.“外方内圆”与“外圆内方”是我国古代建筑常见的设计,如图中外面正方形的面积是,则内圆的面积是( ),如果外圆的面积是,则圆内正方形的面积是( )。
三、判断题
13.任何圆的周长都是直径的3.14倍。( )
14.下水道井盖平面轮廓做成圆形的,圆形井盖怎么放都不会掉到井里,并且能恰好盖住井口,是利用了同一圆中直径都相等的性质。( )
15.如果大、小圆的半径比是3∶2,那么它们的面积比是9∶4。( )
16.半径为r的一个半圆,其周长是。( )
17.一张圆形的纸,想用对折的方法确定圆心的位置,则至少对折2次。( )
四、计算题
18.求图中涂色部分的周长。(单位:cm)
19.如图,等腰直角三角形的一条直角边和半圆的直径重合,求阴影部分的面积。
五、解答题
20.一辆自行车轮胎的外半径是0.3米。如果每分钟转100周,通过一座1000米长的桥需要几分钟?(得数保留一位小数)
21.为了丰富学生的课后延时活动,手工社团的同学用一根铁丝围成一个长10厘米,宽5.7厘米的长方形,又用这根铁丝围成了一个最大的圆形,这个圆形的面积是多少?
22.李叔叔计划在边长8米的正方形天台上用油漆涂出一个最大的圆用于布置,若每平方米需要用油漆0.5千克,需要多少千克油漆?
23.如下图中的圆从点A开始,沿着直尺(单位:cm)向右滚动一周,到达点B。
(1)点B大约在哪里?请在图中的直尺上标出来。
(2)这个圆的面积是( )平方厘米。
24.社团制作木质三角形轨道:一个半径1cm的圆从B点出发,沿着边长6厘米的等边三角形的外壁滚动(无滑动),最后回到原来的位置。圆心经过的路程是多少厘米?(取3)
参考答案:
1.B
【分析】沿着一条直线将图形对折,两边的图形能够完全重合,这个图形叫做轴对称图形,这条直线是图形的对称轴,据此解答即可。
【详解】圆的对称轴有无数条,圆的对称轴是圆的直径所在直线,正方形有4条对称轴,这4条对称轴都是圆的直径所在直线,所以这个组合图形有4条对称轴。
故答案为:B
【点睛】本题考查对称轴、圆,解答本题的关键是掌握对称轴的概念。
2.C
【分析】需要分别求出长方形和梯形中阴影部分的扇形组成的图形的面积,长方形中四个四分之一圆的半径相等就能拼成一个整圆,根据圆的面积公式=π×半径2,即可求出长方形中圆的面积,梯形中阴影部分的扇形就能拼成一个整圆,面积同样为根据圆的面积公式=π×半径2,即可求出梯形中圆的面积,然后两者比较大小即可。
【详解】长方形中圆的面积:
S=π×半径2
=3.14×12
=3.14×1
=3.14(平方厘米)
梯形中圆的面积:
S=π×半径2
=3.14×12
=3.14×1
=3.14(平方厘米)
3.14=3.14,长方形中圆的面积和梯形中圆的面积一样大。
故答案为:C
3.D
【分析】这条小路的面积也就是圆环的面积,圆环的面积=大圆的面积-小圆的面积;根据圆的面积=πr2,大圆的半径是(6+2)米,小圆的半径是6米,代入相应数值计算,据此解答。
【详解】π×(6+2)2-π×62
=π×82-π×62
=π×(82-62)
=π×(64-36)
=28π(平方米)
因此这条小路的面积是(28π)平方米。
故答案为:D
4.B
【分析】把一个圆剪拼成一个近似的长方形,长方形的长等于圆的周长的一半,宽等于圆的半径;拼成的长方形的周长比原来圆的周长增加了2条宽的长度,即增加了2个半径的长度,据此解答。
【详解】10÷2×2=10(厘米)
拼成的图形的周长比原来圆的周长增加10厘米。
故答案为:B
5.B
【分析】由题意可知:正方形里剪一个最大的圆,圆的直径等于正方形边长时正方形最小,用圆的面积÷π,求出半径的平方,确定半径,求出直径,即正方形边长。
【详解】12.56÷3.14=4(平方厘米)
4=2×2
2×2=4(厘米)
所以正方形边长至少为4厘米。
故答案为:B
6.A
【分析】根据比的意义,写出各选项中两个量的比,再化简比,找出两个量的比可以用5∶4表示的选项即可。
【详解】①150∶120
=(150÷30)∶(120÷30)
=5∶4
哥哥与妹妹的身高之比是5∶4;
②橡皮的总价与数量之比是5∶4;
③(π×52)∶(π×42)
=25π∶16π
=25∶16
大圆与小圆的面积之比是25∶16,不能用5∶4表示;
故答案为:A
7.314
【分析】将数据代入圆的周长公式:C=2πr求出圆形羊栏的周长,再乘5即可。
【详解】3.14×2×10×5
=6.28×10×5
=62.8×5
=314(米)
至少要用314米的铁丝才能把羊栏围上5圈。
8. 3∶2 9∶4
【分析】将数据代入圆的周长公式:C=2πr及圆的面积公式S=πr2,分别求出大、小圆的周长,面积,写出周长比、面积比后化简即可。
【详解】小圆周长:π×2×4=8π(米)
小圆面积:π×42=16π(米)
大圆周长:π×2×6=12π(平方米)
大圆面积:π×62=36π(平方米)
大圆周长∶小圆周长=12π米∶8π米=3∶2
大圆面积∶小圆面积=36π平方米∶16π平方米=9∶4
小圆的半径是4米,大圆的半径是6米,大圆和小圆的周长比是3∶2,大圆和小圆的面积比是9∶4。
9. 15.42 14.13
【分析】由题意知:半圆的周长是圆周长一半加一条直径,半圆的面积是圆面积的一半。利用圆的周长计算公式,圆的面积计算公式,将数值代入计算即可。据此解答。
【详解】3.14×6÷2+6
=18.84÷2+6
=9.42+6
=15.42(米)
6÷2=3(米)
=28.26÷2
=14.13(平方米)
这个半圆形的花坛的周长是(15.42)m,面积是(14.13)m2。
【点睛】灵活运用圆的周长和面积计算公式是解答的关键。
10.125.6
【分析】从图中可知,正方形的边长等于圆的半径,根据正方形的面积公式S=a2可知,正方形的面积正好是r2,即r2=40,把r2的值代入圆的面积公式S=πr2中计算,即可求出圆的面积。
【详解】3.14×40=125.6(cm2)
圆的面积是125.6 cm2。
11.78.5
【分析】由图可知,平行四边形的高等于圆的半径,底等于圆周长的一半;根据圆的周长公式:C=2πr可得r=C÷2π,代入数据求出半径(也就是平行四边形的高),再代入平行四边形的面积公式:S=ah计算即可。
【详解】15.7×2÷2÷3.14
=31.4÷2÷3.14
=15.7÷3.14
=5(cm)
15.7×5=78.5(cm2)
这个平行四边形的面积是78.5cm2。
12. 12.56 18
【分析】根据正方形面积公式:面积=边长×边长;正方形面积是16dm2,4×4=16,所以正方形边长是4dm;正方形内最大的圆,圆的直径等于正方形的边长;圆的直径等于4dm;根据圆的面积公式:面积=π×半径2,代入数据,求出内圆的面积;
根据圆的面积公式:面积=π×半径2,半径2=面积÷π;用9π÷π=9,求出半径的平方;3×3=9,所以外圆的半径是3dm;圆内正方形的面积=直径×半径,据此求出圆内正方形的面积。
【详解】4×4=16;正方形的边长是4dm;
园内面积:3.14×(4÷2)2
=3.14×22
=3.14×4
=12.56(dm2)
9π÷π=9
3×3=9;外圆的半径是3dm。
3×2×3
=6×3
=18(dm2)
“外方内圆”与“外圆内方”是我国古代建筑常见的设计,外面正方形的面积16dm2,则内圆的面积是12.56dm2,如果外圆的面积是9πdm2,则圆内正方形的面积是18dm2。
13.×
【分析】根据教材中关于圆周率的含义的推导可知,圆的周长和它直径的比值,叫做圆周率,圆周率用“π”表示,π的取值是3.14159265…;由此判断即可。
【详解】一个圆的周长总是直径的π倍,π约等于3.14,并不等于3.14,原题说法错误。
故答案为:×
【点睛】此题的关键在于区分π和3.14的区别。
14.√
【分析】同圆或等圆中,所有的直径都相等,因此这就是圆形井盖设计成圆形的原因。
【详解】下水道井盖平面轮廓做成圆形的,圆形井盖怎么放都不会掉到井里,并且能恰好盖住井口,是利用了同一圆中直径都相等的性质,说法正确。
故答案为:√
【点睛】关键是熟悉圆的特征,根据圆的特征进行分析。
15.√
【分析】由题意可知,大、小圆的半径比是3∶2,则假设大、小圆的半径为3和2,再根据圆的面积公式:S=πr2,据此求出大、小圆的面积,进而求出它们的面积比。
【详解】假设大、小圆的半径为3和2
32π∶22π
=9π∶4π
=(9π÷π)∶(4π÷π)
=9∶4
则它们的面积比是9∶4。原题说法正确。
故答案为:√
【点睛】本题考查比的应用,结合圆的面积的计算方法是解题的关键。
16.√
【分析】根据圆的周长公式可计算出圆的周长,那么半圆的周长是圆周长的一半加上一条直径,由此解答即可。
【详解】半圆的周长:
=
=
故答案为:√
【点睛】此题考查的是圆的周长公式的灵活运用,要认真审题。
17.√
【分析】圆中心的那个点即圆心,所有直径都相交于圆心,将一个圆形纸片最少要对折两次,才能找到两条折痕相交的那个点,即圆心。
【详解】由分析可得:一张圆形的纸,想用对折的方法确定圆心的位置,则至少对折2次,原题说法正确。
故答案为:√
【点睛】本题考查了确定圆心的方法。
18.43.96cm
【分析】观察图形可知,涂色部分的周长=直径为(5+9)cm圆周长的一半+直径为9cm圆周长的一半+直径为5cm圆周长的一半,根据圆的周长公式C=πd,代入数据计算求解。
【详解】3.14×(5+9)÷2+3.14×9÷2+3.14×5÷2
=3.14×14÷2+3.14×9÷2+3.14×5÷2
=21.98+14.13+7.85
=43.96(cm)
涂色部分的周长是43.96cm。
19.25平方厘米
【分析】
如上图,添加两道红色辅助线,将A处阴影面积割补到B处后,阴影面积是一个底为10厘米,高为5厘米的等腰三角形面积。据此三角形面积=底×高÷2,将数值代入计算即可。
【详解】10×5÷2
=50÷2
=25(平方厘米)
阴影部分的面积是25平方厘米。
【点睛】根据等腰三角形特征,利用割补法,将不规则的阴影面积转换为规则图形的面积是解答的关键。
20.5.3分钟
【分析】先根据圆的周长公式C=2πr,求出自行车车轮转一周行驶的距离,再乘100周,即可求出自行车每分钟行驶的距离;然后用桥的长度除以自行车每分钟行驶的距离,求出自行车通过这座桥所需的时间。
【详解】2×3.14×0.3×100
=6.28×0.3×100
=1.884×100
=188.4(米)
1000÷188.4≈5.3(分钟)
答:通过一座1000米长的桥需要5.3分钟。
21.78.5平方厘米
【分析】根据长方形的周长=(长+宽)×2,求出这根铁丝的长度,再根据圆的周长=2×π×半径,可得半径=圆的周长÷π÷2,最后根据圆的面积=πr ,求出这个圆的面积。
【详解】(10+5.7)×2
=15.7×2
=31.4(厘米)
31.4÷3.14÷2
=10÷2
=5(厘米)
52×3.14
=25×3.14
=78.5(平方厘米)
答:这个圆形的面积是78.5平方厘米。
22.25.12千克
【分析】根据题意可知,圆的直径等于正方形的边长;根据圆的面积公式:面积=π×半径2,代入数据,求出圆的面积,再乘0.5,即求出需要油漆的重量。
【详解】3.14×(8÷2)2×0.5
=3.14×42×0.5
=3.14×16×0.5
=50.24×0.5
=25.12(千克)
答:需要25.12千克油漆。
23.(1)见详解
(2)3.14
【分析】(1)看图可知,圆的直径=3-1=2(厘米),根据圆的周长=πd,求出圆滚动一周的长度,确定B点位置即可;
(2)根据圆的面积公式:面积=πr2,代入数据,即可解答。
【详解】(1)3-1=2(厘米)
3.14×2=6.28(厘米)
2+6.28=8.28(厘米)
如图:
(2)3.14×(2÷2)2
=3.14×12
=3.14×1
=3.14(平方厘米)
圆的面积是3.14平方厘米。
24.24厘米
【分析】
圆心经过的路线如图,改路线由3条6厘米的线段与3条半径是1厘米,圆心角是(360°-90°×2-60°)的扇形的弧组成,这3条扇形的弧长总和恰好是1个半径1厘米的圆的周长,圆的周长=2×圆周率×半径,据此列式解答。
【详解】6×3+2×3×1
=18+6
=24(厘米)
答:圆心经过的路程是24厘米。
【点睛】关键是弄清楚圆心经过的路线,掌握并灵活运用圆的周长公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
