高中数学《3.3幂函数》 课件(共20张PPT)
文档属性
| 名称 | 高中数学《3.3幂函数》 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-17 16:38:49 | ||
图片预览





文档简介
(共20张PPT)
3.3幂函数
2019人教版必修1第一册第三章
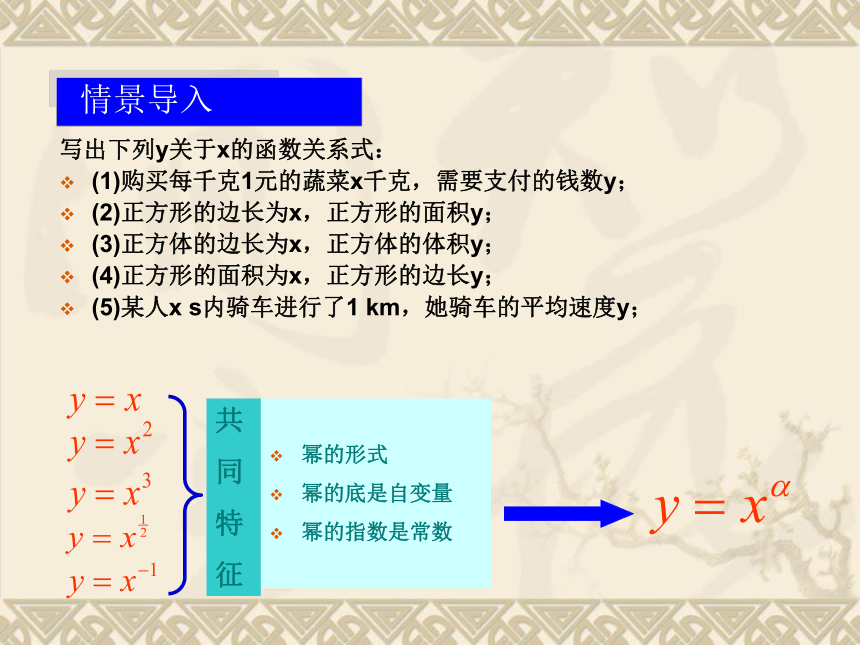
写出下列y关于x的函数关系式:
(1)购买每千克1元的蔬菜x千克,需要支付的钱数y;
(2)正方形的边长为x,正方形的面积y;
(3)正方体的边长为x,正方体的体积y;
(4)正方形的面积为x,正方形的边长y;
(5)某人x s内骑车进行了1 km,她骑车的平均速度y;
情景导入
幂的形式
幂的底是自变量
幂的指数是常数
共
同
特
征
幂函数的定义
幂函数的定义:一般地函数 叫做幂函数,其中x是自变量,α是常数。
小试牛刀
1、判断下列函数是否是幂函数
2、若函数 是幂函数,求a的值。
是
否
否
否
是
否
规律
总结
的系数是1
底数是单一的x
指数是常数
-1或4
对于幂函数,我们先讨论α=1,2,3, 时的情景,
即先讨论函数
幂函数的定义
幂函数的定义:一般地函数 叫做幂函数
其中x是自变量,α是常数。
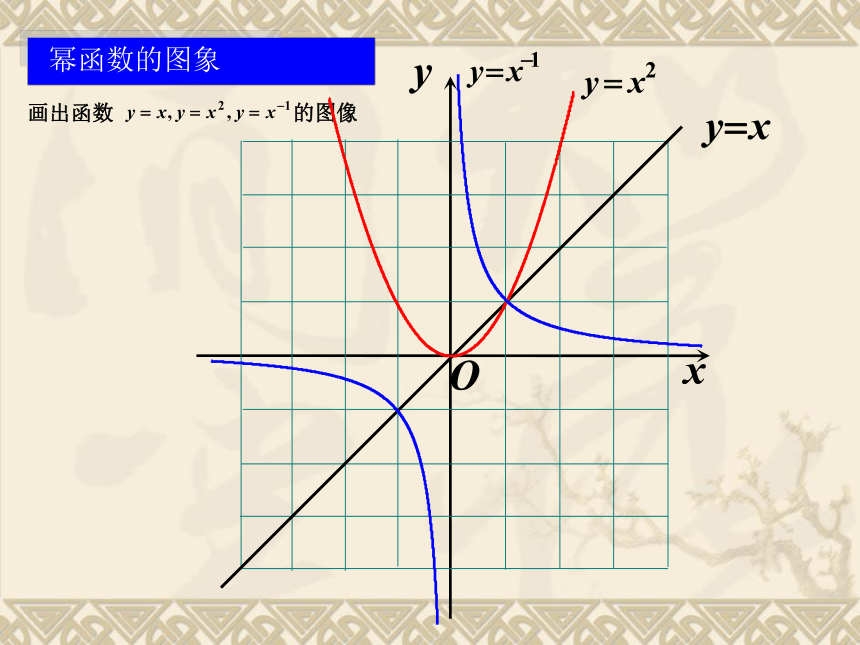
幂函数的图象
画出函数 的图像
y
x
O
y
x
O
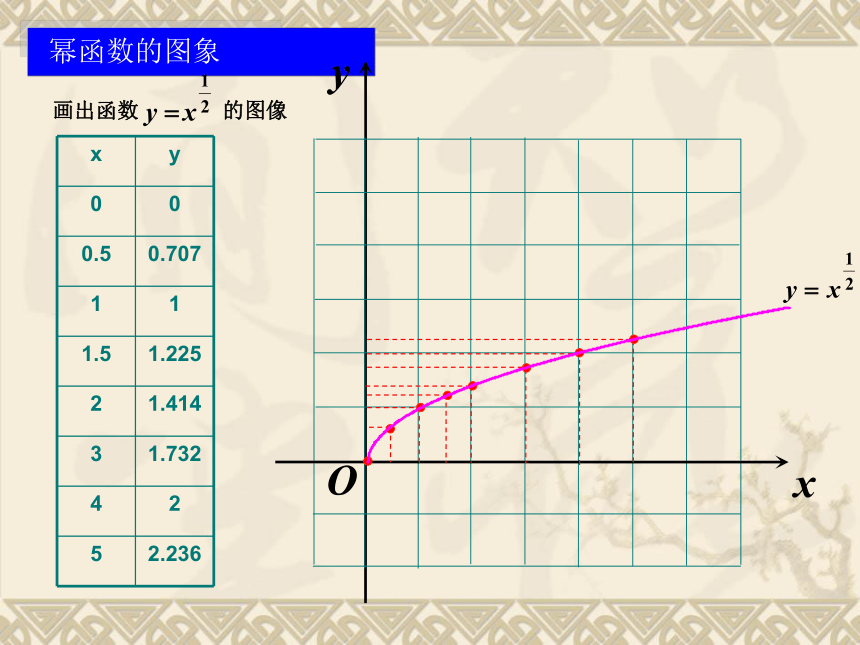
幂函数的图象
x y
0 0
0.5 0.707
1 1
1.5 1.225
2 1.414
3 1.732
4 2
5 2.236
画出函数 的图像
y
x
O
幂函数的图象
x y
1.5 3.375
1 1
0.5 0.125
0 0
画出函数 的图像
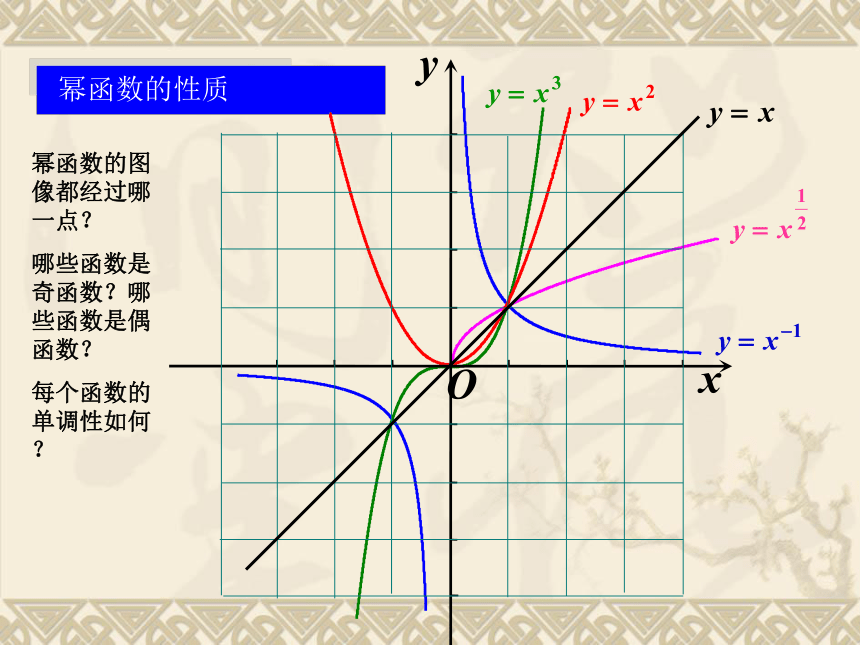
幂函数的性质
y
x
O
幂函数的图像都经过哪一点?
哪些函数是奇函数?哪些函数是偶函数?
每个函数的单调性如何?
x
O
y
R
R
奇
增
y
x
O
(0,+∞)
R
偶
(-∞,0)减
(0,+∞)增
y
x
O
R
R
奇
增
y
x
O
[0,+∞)
非奇非偶
增
[0,+∞)
幂函数的性质
(1,1)
函数 的图像都
过点(1,1)
函数 是奇函数,函数
是偶函数
在区间 上,函数 是增函数,函数 是减函数
在第一向限内,函数 的图像向上与y轴无限的接近,向右与x轴无限的接近。
幂函数的性质
例. 证明幂函数 在[0,+∞)上是增函数.
证明:任取x1,x2∈ [0,+∞),且x1<x2,则
解(1)
上是增函数,1.1< 1.4
∴
幂函数性质的应用
5
0
5
.
)
(
.
1
1
例1 比较下列各组中值的大小,并说明理由
.
0
2
;
4
1
,
.
1
)
(
(2)
上是增函数, ,且 1<1.5<1.7
∴
比较幂值大小关键是看指数是否相同,若指数相同则可以利用幂函数的单调性来判断的大小。
规律总结
课堂练习
c
1、下列函数不是幂函数的是( )
A B C D
2、如图所示,曲线是幂函数 在
第一象限内的图像,已知α分别取
四个值,则相应图像以此为
3、若幂函数y=f(x)的图像经过点(9,3),则f(25)=
4、比较下列各组数的大小:
(1) (2)
5、幂函数 在区间(0,+∞)上是减函数,
则m的值为
y
x
O
了解幂函数的概念
会画常见幂函数的图象
结合图像了解幂函数图象的变化情况和简单性质
会用幂函数的单调性比较两个底数不同而指数相同的幂的大小
课堂小结
3.3幂函数
2019人教版必修1第一册第三章
写出下列y关于x的函数关系式:
(1)购买每千克1元的蔬菜x千克,需要支付的钱数y;
(2)正方形的边长为x,正方形的面积y;
(3)正方体的边长为x,正方体的体积y;
(4)正方形的面积为x,正方形的边长y;
(5)某人x s内骑车进行了1 km,她骑车的平均速度y;
情景导入
幂的形式
幂的底是自变量
幂的指数是常数
共
同
特
征
幂函数的定义
幂函数的定义:一般地函数 叫做幂函数,其中x是自变量,α是常数。
小试牛刀
1、判断下列函数是否是幂函数
2、若函数 是幂函数,求a的值。
是
否
否
否
是
否
规律
总结
的系数是1
底数是单一的x
指数是常数
-1或4
对于幂函数,我们先讨论α=1,2,3, 时的情景,
即先讨论函数
幂函数的定义
幂函数的定义:一般地函数 叫做幂函数
其中x是自变量,α是常数。
幂函数的图象
画出函数 的图像
y
x
O
y
x
O
幂函数的图象
x y
0 0
0.5 0.707
1 1
1.5 1.225
2 1.414
3 1.732
4 2
5 2.236
画出函数 的图像
y
x
O
幂函数的图象
x y
1.5 3.375
1 1
0.5 0.125
0 0
画出函数 的图像
幂函数的性质
y
x
O
幂函数的图像都经过哪一点?
哪些函数是奇函数?哪些函数是偶函数?
每个函数的单调性如何?
x
O
y
R
R
奇
增
y
x
O
(0,+∞)
R
偶
(-∞,0)减
(0,+∞)增
y
x
O
R
R
奇
增
y
x
O
[0,+∞)
非奇非偶
增
[0,+∞)
幂函数的性质
(1,1)
函数 的图像都
过点(1,1)
函数 是奇函数,函数
是偶函数
在区间 上,函数 是增函数,函数 是减函数
在第一向限内,函数 的图像向上与y轴无限的接近,向右与x轴无限的接近。
幂函数的性质
例. 证明幂函数 在[0,+∞)上是增函数.
证明:任取x1,x2∈ [0,+∞),且x1<x2,则
解(1)
上是增函数,1.1< 1.4
∴
幂函数性质的应用
5
0
5
.
)
(
.
1
1
例1 比较下列各组中值的大小,并说明理由
.
0
2
;
4
1
,
.
1
)
(
(2)
上是增函数, ,且 1<1.5<1.7
∴
比较幂值大小关键是看指数是否相同,若指数相同则可以利用幂函数的单调性来判断的大小。
规律总结
课堂练习
c
1、下列函数不是幂函数的是( )
A B C D
2、如图所示,曲线是幂函数 在
第一象限内的图像,已知α分别取
四个值,则相应图像以此为
3、若幂函数y=f(x)的图像经过点(9,3),则f(25)=
4、比较下列各组数的大小:
(1) (2)
5、幂函数 在区间(0,+∞)上是减函数,
则m的值为
y
x
O
了解幂函数的概念
会画常见幂函数的图象
结合图像了解幂函数图象的变化情况和简单性质
会用幂函数的单调性比较两个底数不同而指数相同的幂的大小
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
