鲁教版九年级数学上册第五章圆复习学案
图片预览


文档简介
鲁教版九年级数学上册总复习——圆(含答案)
一、知识梳理
(一)圆的对称性
1、垂径定理及推论:
2、圆心角、弧、弦之间的关系:
3、圆心角定理:
4、圆周角定理及推论:
(二)直线与圆的位置关系
1、数量关系:
2、切线的判定和性质定理:
3、切线长定理:
(三)圆的有关计算
1、弧长公式
2、扇形面积公式:
3、圆锥侧面展开图的计算公式:
二、基础练习
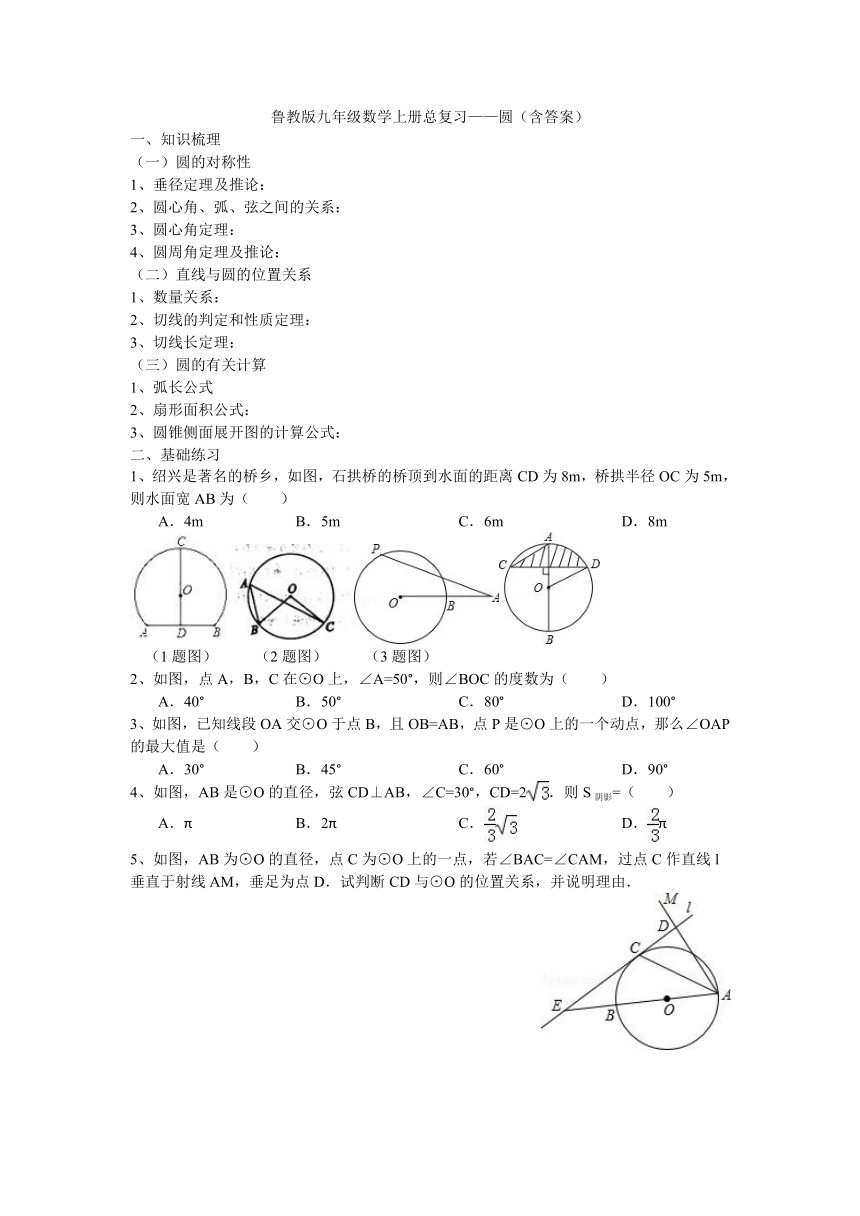
1、绍兴是著名的桥乡,如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为( )
A.4m B. 5m C. 6m D. 8m
(1题图) (2题图) (3题图)
2、如图,点A,B,C在⊙O上,∠A=50°,则∠BOC的度数为( )
A.40° B. 50° C. 80° D. 100°
3、如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )
A.30° B. 45° C. 60° D. 90°
4、如图,AB是⊙O的直径,弦CD⊥AB,∠C=30°,CD=2.则S阴影=( )
A.π B. 2π C. D. π
5、如图,AB为⊙O的直径,点C为⊙O上的一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.试判断CD与⊙O的位置关系,并说明理由.
三、典例精析
6、如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( )
A.12π B. 24π C. 6π D. 36π
(6题图) (8题图)
7、半径为R的圆中,有一弦恰好等于半径,则弦所对的圆心角为 .
8、如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为的中点.若∠A=40°,则∠B= 度.
9、如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=8,求CD的长.
10、如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
四、对应训练
11、如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连接CD.如果∠BAC=20°,则∠BDC=( )
A.80° B.70° C.60° D.50°
12、如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为( )
A.25° B.30° C.50° D.65°
(11题图) (12题图) (13题图) (14题图)
13、如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为()
A.50° B.80° C.100° D.130°
14、如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( )
A.40° B.50° C.80° D.100°
15、若⊙O的半径为4,圆心O到直线l的距离为5,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
16、如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=60°,则∠P为( )
A.120° B.60° C.30° D.45°
(16题图) (17题图) (18题图)
17、如图,从一块直径是8m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )m.
A.4 B.5 C. D.2
18、如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
五、中考体验
19、(2015?泰安)如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
A.+ B. +π C. ﹣ D. 2+
20、(2015?泰安)如图,AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=65°,则∠E= .
21、(2014年泰安)如图,半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( )
A.(﹣1)cm2 B. (+1)cm2 C. 1cm2 D. cm2
(19题图) (20题图) (21题图) (22题图)
22、(2014年泰安)如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则sinα的值为 .
23、(2013?泰安)如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是( )
A.OC∥AE B.EC=BC C.∠DAE=∠ABE D.AC⊥OE
(23题图) (24题图)
24、(2013?泰安)如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为( )
A.8 B.4 C.4π+4 D.4π﹣4
六、课堂达标
25、如图,⊙O中,如果=2,那么( )
A.AB=AC B.AB=2AC C.AB<2AC D.AB>2AC
26、如图,已知⊙O的半径为10,弦AB=12,M是AB上任意一点,则线段OM的长可能是( )
A.5 B.7 C.9 D.11
27、小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A.第一块 B.第二块 C.第三块 D.第四块
28、已知⊙O的直径是10,圆心O到直线l的距离是5,则直线l和⊙O的位置关系是( )
A.相离 B.相交 C.相切 D.外切
29、如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
30、已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3 B.9 C.18 D.36
31、(2015?临沂)如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).
参考答案
1、D 2、D 3、A 4、D
5、
6、B7、60° 8、70 9、(1)证明:连接AC,如图
∵直径AB垂直于弦CD于点E,∴,∴AC=AD,
∵过圆心O的线CF⊥AD,∴AF=DF,即CF是AD的中垂线,∴AC=CD,
∴AC=AD=CD.即:△ACD是等边三角形,∴∠FCD=30°,
在Rt△COE中,,∴,∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=8,∴,
又∵BE=OE,∴OE=2,∴,∴.
10、(1)证明:连接OD,∵OB=OD,∴∠ABC=∠ODB,
∵AB=AC,∴∠ABC=∠ACB,∴∠ODB=∠ACB,∴OD∥AC,
∵DF是⊙O的切线,∴DF⊥OD,∴DF⊥AC.
(2)解:连接OE,∵DF⊥AC,∠CDF=22.5°,∴∠ABC=∠ACB=67.5°,∴∠BAC=45°,
∵OA=OE,∴∠AOE=90°,∵⊙O的半径为4,∴S扇形AOE=4π,S△AOE=8 ,∴S阴影=4π﹣8.1.B;12.C;13.D;14.C;15.C;16.B;17.C;
18、解:(1)∵AB与圆O相切,∴OD⊥AB,
在Rt△BDO中,BD=2,tan∠BOD==,∴OD=3;
(2)连接OE,
∵AE=OD=3,AE∥OD,∴四边形AEOD为平行四边形,∴AD∥EO,
∵DA⊥AE,∴OE⊥AC,又∵OE为圆的半径,∴AE为圆O的切线;
(3)∵OD∥AC,∴=,即=,∴AC=7.5,∴EC=AC﹣AE=7.5﹣3=4.5,
∴S阴影=S△BDO+S△OEC﹣S扇形FOD﹣S扇形EOG
=×2×3+×3×4.5﹣
=3+﹣
=.
19、A.20、 50° .21、A.22、 23、D 24、A
25、C;26、C;27、A;28、C;29、A;30、C;
31、(1)证明:∵⊙O切BC于D,∴OD⊥BC,
∵AC⊥BC,∴AC∥OD,∴∠CAD=∠ADO,
∵OA=OD,∴∠OAD=∠ADO,∴∠OAD=∠CAD,即AD平分∠CAB;
(2)设EO与AD交于点M,连接ED.
∵∠BAC=60°,OA=OE,∴∠AEO是等边三角形,∴AE=OA,∠AOE=60°,
∴AE=AO=OD,
又由(1)知,AC∥OD即AE∥OD,
∴四边形AEDO是菱形,则△AEM≌△DMO,∠EOD=60°,
∴S△AEM=S△DMO,
∴S阴影=S扇形EOD==.
一、知识梳理
(一)圆的对称性
1、垂径定理及推论:
2、圆心角、弧、弦之间的关系:
3、圆心角定理:
4、圆周角定理及推论:
(二)直线与圆的位置关系
1、数量关系:
2、切线的判定和性质定理:
3、切线长定理:
(三)圆的有关计算
1、弧长公式
2、扇形面积公式:
3、圆锥侧面展开图的计算公式:
二、基础练习
1、绍兴是著名的桥乡,如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为( )
A.4m B. 5m C. 6m D. 8m
(1题图) (2题图) (3题图)
2、如图,点A,B,C在⊙O上,∠A=50°,则∠BOC的度数为( )
A.40° B. 50° C. 80° D. 100°
3、如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )
A.30° B. 45° C. 60° D. 90°
4、如图,AB是⊙O的直径,弦CD⊥AB,∠C=30°,CD=2.则S阴影=( )
A.π B. 2π C. D. π
5、如图,AB为⊙O的直径,点C为⊙O上的一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.试判断CD与⊙O的位置关系,并说明理由.
三、典例精析
6、如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( )
A.12π B. 24π C. 6π D. 36π
(6题图) (8题图)
7、半径为R的圆中,有一弦恰好等于半径,则弦所对的圆心角为 .
8、如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为的中点.若∠A=40°,则∠B= 度.
9、如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=8,求CD的长.
10、如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
四、对应训练
11、如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连接CD.如果∠BAC=20°,则∠BDC=( )
A.80° B.70° C.60° D.50°
12、如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为( )
A.25° B.30° C.50° D.65°
(11题图) (12题图) (13题图) (14题图)
13、如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为()
A.50° B.80° C.100° D.130°
14、如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( )
A.40° B.50° C.80° D.100°
15、若⊙O的半径为4,圆心O到直线l的距离为5,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
16、如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=60°,则∠P为( )
A.120° B.60° C.30° D.45°
(16题图) (17题图) (18题图)
17、如图,从一块直径是8m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )m.
A.4 B.5 C. D.2
18、如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
五、中考体验
19、(2015?泰安)如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
A.+ B. +π C. ﹣ D. 2+
20、(2015?泰安)如图,AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=65°,则∠E= .
21、(2014年泰安)如图,半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( )
A.(﹣1)cm2 B. (+1)cm2 C. 1cm2 D. cm2
(19题图) (20题图) (21题图) (22题图)
22、(2014年泰安)如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则sinα的值为 .
23、(2013?泰安)如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是( )
A.OC∥AE B.EC=BC C.∠DAE=∠ABE D.AC⊥OE
(23题图) (24题图)
24、(2013?泰安)如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为( )
A.8 B.4 C.4π+4 D.4π﹣4
六、课堂达标
25、如图,⊙O中,如果=2,那么( )
A.AB=AC B.AB=2AC C.AB<2AC D.AB>2AC
26、如图,已知⊙O的半径为10,弦AB=12,M是AB上任意一点,则线段OM的长可能是( )
A.5 B.7 C.9 D.11
27、小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )
A.第一块 B.第二块 C.第三块 D.第四块
28、已知⊙O的直径是10,圆心O到直线l的距离是5,则直线l和⊙O的位置关系是( )
A.相离 B.相交 C.相切 D.外切
29、如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
30、已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3 B.9 C.18 D.36
31、(2015?临沂)如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).
参考答案
1、D 2、D 3、A 4、D
5、
6、B7、60° 8、70 9、(1)证明:连接AC,如图
∵直径AB垂直于弦CD于点E,∴,∴AC=AD,
∵过圆心O的线CF⊥AD,∴AF=DF,即CF是AD的中垂线,∴AC=CD,
∴AC=AD=CD.即:△ACD是等边三角形,∴∠FCD=30°,
在Rt△COE中,,∴,∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=8,∴,
又∵BE=OE,∴OE=2,∴,∴.
10、(1)证明:连接OD,∵OB=OD,∴∠ABC=∠ODB,
∵AB=AC,∴∠ABC=∠ACB,∴∠ODB=∠ACB,∴OD∥AC,
∵DF是⊙O的切线,∴DF⊥OD,∴DF⊥AC.
(2)解:连接OE,∵DF⊥AC,∠CDF=22.5°,∴∠ABC=∠ACB=67.5°,∴∠BAC=45°,
∵OA=OE,∴∠AOE=90°,∵⊙O的半径为4,∴S扇形AOE=4π,S△AOE=8 ,∴S阴影=4π﹣8.1.B;12.C;13.D;14.C;15.C;16.B;17.C;
18、解:(1)∵AB与圆O相切,∴OD⊥AB,
在Rt△BDO中,BD=2,tan∠BOD==,∴OD=3;
(2)连接OE,
∵AE=OD=3,AE∥OD,∴四边形AEOD为平行四边形,∴AD∥EO,
∵DA⊥AE,∴OE⊥AC,又∵OE为圆的半径,∴AE为圆O的切线;
(3)∵OD∥AC,∴=,即=,∴AC=7.5,∴EC=AC﹣AE=7.5﹣3=4.5,
∴S阴影=S△BDO+S△OEC﹣S扇形FOD﹣S扇形EOG
=×2×3+×3×4.5﹣
=3+﹣
=.
19、A.20、 50° .21、A.22、 23、D 24、A
25、C;26、C;27、A;28、C;29、A;30、C;
31、(1)证明:∵⊙O切BC于D,∴OD⊥BC,
∵AC⊥BC,∴AC∥OD,∴∠CAD=∠ADO,
∵OA=OD,∴∠OAD=∠ADO,∴∠OAD=∠CAD,即AD平分∠CAB;
(2)设EO与AD交于点M,连接ED.
∵∠BAC=60°,OA=OE,∴∠AEO是等边三角形,∴AE=OA,∠AOE=60°,
∴AE=AO=OD,
又由(1)知,AC∥OD即AE∥OD,
∴四边形AEDO是菱形,则△AEM≌△DMO,∠EOD=60°,
∴S△AEM=S△DMO,
∴S阴影=S扇形EOD==.
