苏科版(2024)七上数学:2.3.1绝对值与相反数:绝对值(同步课件)
文档属性
| 名称 | 苏科版(2024)七上数学:2.3.1绝对值与相反数:绝对值(同步课件) |  | |
| 格式 | pptx | ||
| 文件大小 | 40.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 14:07:10 | ||
图片预览




文档简介
(共18张PPT)
第2章 有理数
2.3.1绝对值与相反数:绝对值
教学目标
理解绝对值的概念,会求一个数的绝对值
能运用绝对值进行运算
01
02
绝对值的概念与运算
小明家在学校正西方3km处,小丽家在学校正东方2km处。用数轴上的点表示学校、小明家、小丽家的位置。
01
课堂引入
小明家
学校
小丽家
西
东
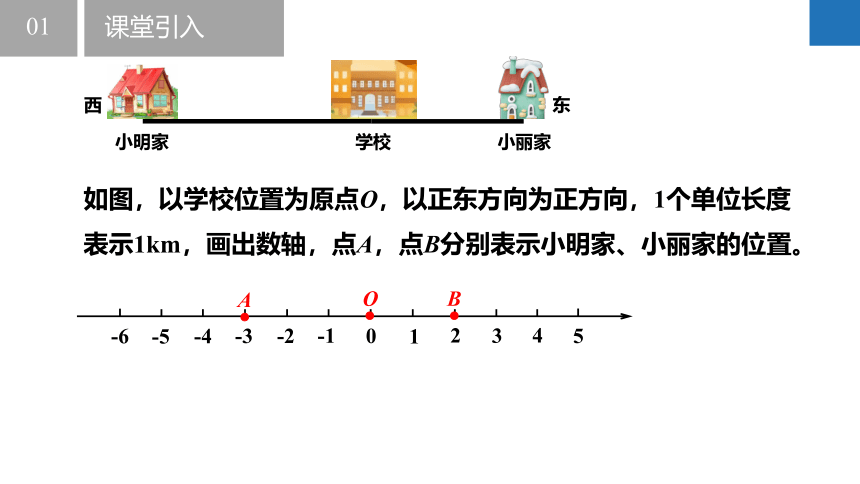
如图,以学校位置为原点O,以正东方向为正方向,1个单位长度表示1km,画出数轴,点A,点B分别表示小明家、小丽家的位置。
01
课堂引入
小明家
学校
小丽家
西
东
1
2
3
4
-4
-1
-2
-3
0
-5
-6
5
O
A
B
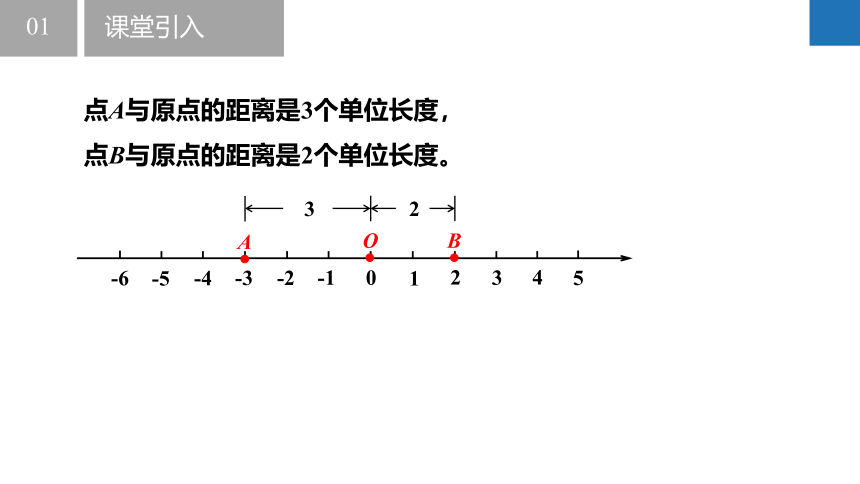
点A与原点的距离是3个单位长度,点B与原点的距离是2个单位长度。
01
课堂引入
1
2
3
4
-4
-1
-2
-3
0
-5
-6
5
O
A
B
3
2
eg:-3的绝对值记为|-3|,-3与原点的距离为3,即|-3|=3;
2的绝对值记为|2|,2与原点的距离为2,即|2|=2;
0的绝对值记为|0|,0与原点的距离为0,即|0|=0。
02
知识精讲
绝对值的概念
一般地,数轴上表示一个数的点与原点的距离叫做这个数的绝对值(absolute value)。
数a的绝对值记为|a|,读作“a的绝对值”。
任何一个数的绝对值是非负数。
02
知识精讲
讨论——1.的绝对值是____,-的绝对值是____,0的绝对值是____;
1
2
3
4
-4
-1
-2
-3
0
-
0
02
知识精讲
2.绝对值等于5的数是____,绝对值小于5的整数有____个,
其中绝对值最小的整数是____。
1
2
3
4
-4
-1
-2
-3
0
-5
-6
5
5
5
±5
9
0
由于任意一个有理数的绝对值都是非负数,所以两个有理数的绝对值可以进行小学里学过的各种运算,如:|3|+|-2|=3+2=5。
02
知识精讲
绝对值的运算
“绝对值”运算优先于“加减乘除”运算。
解:(1)原式=1000-197
=1000-200+3
=800+3
=803;
尝试——计算:
(1)|-1000|-|-197|;
(2)|32|×|-2.5|。
02
知识精讲
(2)原式=32×2.5
=8×4×2.5
=8×10
=80。
03
典例精析
例1、分别写出下列各数的绝对值:-1,-6.3,-32,12,3。
|-1|=1
|-6.3|=6.3
|-32|=32
|12|=12
|3|=3
例2、已知|m|=1,|n|=4。
(1)当m、n异号时,求m+n的值;
(2)求m-n的最大值。
03
典例精析
解:(1)∵|m|=1,|n|=4,
∴m=±1,n=±4,
∵m、n异号,
∴①m=1,n=-4,m+n=-3,
②m=-1,n=4,m+n=3,
综上,m+n的值±3;
(2)①m=-1,n=-4,m-n=3,
②m=-1,n=4,m-n=-5,
③m=1,n=-4,m-n=5,
④m=1,n=4,m-n=-3,
∵5>3>-3>-5,
∴m-n的最大值为5。
例3、我们知道|x|=2,则x=±2。
请你那么运用“类比”的数学思想尝试着解决下面两个问题:
(1)|x+3|=2,则x=________;
(2)5-|x-4|=2,则x=________。
03
典例精析
看作整体
解:(1)令a=x+3,
∵|a|=2,
∴a=±2,
∴x+3=-2或x+3=2,
解得:x=-5或x=-1;
-5或-1
(2)整理得:|x-4|=3,令b=x-4,
∵|b|=3,
∴b=±3,
∴x-4=-3或x-4=3,
解得:x=1或x=7。
1或7
解:(1)原式=5.2-7.23+4.8-2.77
=5.2+4.8-(7.23+2.77)
=10-10
=0;
(2)原式=×33+66×+
=×(33+66+1)
=×100
=25。
03
典例精析
例4、(1)|-5.2|-|7.23|+4.8-|-2.77|;
(2)|-|×|33|+66×|-25%|+0.25。
课后总结
绝对值的概念:
一般地,数轴上表示一个数的点与原点的距离叫做这个数的绝对值(absolute value)。
数a的绝对值记为|a|,读作“a的绝对值”。
任何一个数的绝对值是非负数。
绝对值的运算:
“绝对值”运算优先于“加减乘除”运算。
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第2章 有理数
2.3.1绝对值与相反数:绝对值
教学目标
理解绝对值的概念,会求一个数的绝对值
能运用绝对值进行运算
01
02
绝对值的概念与运算
小明家在学校正西方3km处,小丽家在学校正东方2km处。用数轴上的点表示学校、小明家、小丽家的位置。
01
课堂引入
小明家
学校
小丽家
西
东
如图,以学校位置为原点O,以正东方向为正方向,1个单位长度表示1km,画出数轴,点A,点B分别表示小明家、小丽家的位置。
01
课堂引入
小明家
学校
小丽家
西
东
1
2
3
4
-4
-1
-2
-3
0
-5
-6
5
O
A
B
点A与原点的距离是3个单位长度,点B与原点的距离是2个单位长度。
01
课堂引入
1
2
3
4
-4
-1
-2
-3
0
-5
-6
5
O
A
B
3
2
eg:-3的绝对值记为|-3|,-3与原点的距离为3,即|-3|=3;
2的绝对值记为|2|,2与原点的距离为2,即|2|=2;
0的绝对值记为|0|,0与原点的距离为0,即|0|=0。
02
知识精讲
绝对值的概念
一般地,数轴上表示一个数的点与原点的距离叫做这个数的绝对值(absolute value)。
数a的绝对值记为|a|,读作“a的绝对值”。
任何一个数的绝对值是非负数。
02
知识精讲
讨论——1.的绝对值是____,-的绝对值是____,0的绝对值是____;
1
2
3
4
-4
-1
-2
-3
0
-
0
02
知识精讲
2.绝对值等于5的数是____,绝对值小于5的整数有____个,
其中绝对值最小的整数是____。
1
2
3
4
-4
-1
-2
-3
0
-5
-6
5
5
5
±5
9
0
由于任意一个有理数的绝对值都是非负数,所以两个有理数的绝对值可以进行小学里学过的各种运算,如:|3|+|-2|=3+2=5。
02
知识精讲
绝对值的运算
“绝对值”运算优先于“加减乘除”运算。
解:(1)原式=1000-197
=1000-200+3
=800+3
=803;
尝试——计算:
(1)|-1000|-|-197|;
(2)|32|×|-2.5|。
02
知识精讲
(2)原式=32×2.5
=8×4×2.5
=8×10
=80。
03
典例精析
例1、分别写出下列各数的绝对值:-1,-6.3,-32,12,3。
|-1|=1
|-6.3|=6.3
|-32|=32
|12|=12
|3|=3
例2、已知|m|=1,|n|=4。
(1)当m、n异号时,求m+n的值;
(2)求m-n的最大值。
03
典例精析
解:(1)∵|m|=1,|n|=4,
∴m=±1,n=±4,
∵m、n异号,
∴①m=1,n=-4,m+n=-3,
②m=-1,n=4,m+n=3,
综上,m+n的值±3;
(2)①m=-1,n=-4,m-n=3,
②m=-1,n=4,m-n=-5,
③m=1,n=-4,m-n=5,
④m=1,n=4,m-n=-3,
∵5>3>-3>-5,
∴m-n的最大值为5。
例3、我们知道|x|=2,则x=±2。
请你那么运用“类比”的数学思想尝试着解决下面两个问题:
(1)|x+3|=2,则x=________;
(2)5-|x-4|=2,则x=________。
03
典例精析
看作整体
解:(1)令a=x+3,
∵|a|=2,
∴a=±2,
∴x+3=-2或x+3=2,
解得:x=-5或x=-1;
-5或-1
(2)整理得:|x-4|=3,令b=x-4,
∵|b|=3,
∴b=±3,
∴x-4=-3或x-4=3,
解得:x=1或x=7。
1或7
解:(1)原式=5.2-7.23+4.8-2.77
=5.2+4.8-(7.23+2.77)
=10-10
=0;
(2)原式=×33+66×+
=×(33+66+1)
=×100
=25。
03
典例精析
例4、(1)|-5.2|-|7.23|+4.8-|-2.77|;
(2)|-|×|33|+66×|-25%|+0.25。
课后总结
绝对值的概念:
一般地,数轴上表示一个数的点与原点的距离叫做这个数的绝对值(absolute value)。
数a的绝对值记为|a|,读作“a的绝对值”。
任何一个数的绝对值是非负数。
绝对值的运算:
“绝对值”运算优先于“加减乘除”运算。
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
