(苏科版2024)七年级上册 2.3.2绝对值与相反数 同步课件 (共36张PPT)
文档属性
| 名称 | (苏科版2024)七年级上册 2.3.2绝对值与相反数 同步课件 (共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 41.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 00:00:00 | ||
图片预览










文档简介
(共36张PPT)
第2章 有理数
2.3.2绝对值与相反数:相反数
教学目标
理解相反数的概念,会求一个数的相反数
掌握多重符号的化简规律
01
02
能利用相反数的性质和判定解决问题
03
相反数的概念
→
借
250元
-250
+250
01
课堂引入
活动——1.如图,观察数轴上表示-4和4的点的位置以及它们到原点的距离,你有什么发现
-4和4关于原点对称,-4和4到原点的距离相等。
01
课堂引入
1
2
3
4
-4
-1
-2
-3
0
继续观察-3和3,-2和2,-1和1,你能得到相同的结论吗?
-3和3,-2和2,-1和1都关于原点对称,
-3和3,-2和2,-1和1到原点的距离都分别相等。
01
课堂引入
1
2
3
4
-4
-1
-2
-3
0
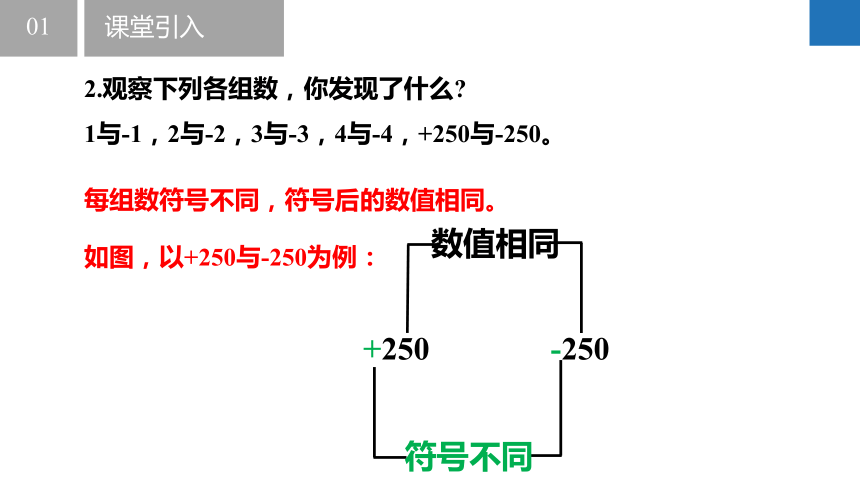
2.观察下列各组数,你发现了什么
1与-1,2与-2,3与-3,4与-4,+250与-250。
+250 -250
符号不同
数值相同
每组数符号不同,符号后的数值相同。
01
课堂引入
如图,以+250与-250为例:
eg:250与-250互为相反数,也可以说250是-250的相反数,-250是250的相反数。
02
知识精讲
相反数的概念
只有符号不同的两个数互为相反数(opposite number),其中一个数叫做另一个数的相反数。
特别地,0的相反数是0。
∵一个数是由符号部分和符号后的数值部分组成,
∴“只有符号不同”,即“符号不同,符号后的数值相同”。
02
知识精讲
相反数的概念
相反数的概念也可以表示:符号不同,符号后的数值相同的两个数互为相反数。
4的相反数是-4
尝试——写出4,-,-4.5的相反数,并在数轴上画出这些数及其相反数对应的点。
-的相反数是
-4.5的相反数是4.5
1
2
3
4
-4
-1
-2
-3
0
-5
-6
5
02
知识精讲
-
-4.5
4.5
1
2
3
4
-4
-1
-2
-3
0
-5
-6
5
-
-4.5
4.5
02
知识精讲
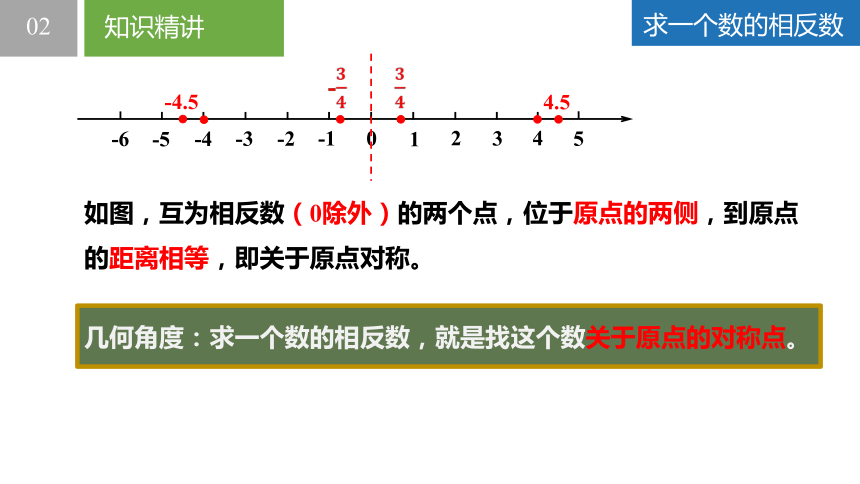
求一个数的相反数
如图,互为相反数(0除外)的两个点,位于原点的两侧,到原点的距离相等,即关于原点对称。
几何角度:求一个数的相反数,就是找这个数关于原点的对称点。
02
知识精讲
求一个数的相反数
代数角度:求一个数的相反数,就是在这个数的前面添加(或删去)一个“-”号。
eg:4添加一个“-”,变成相反数-4;
-删去一个“-”,变成相反数,
-4.5删去一个“-”,变成相反数4.5。
∵互为相反数的两数只相差一个负号,
∴这两个数在数轴上的对应点到原点的距离相等。
由此,我们得到:
互为相反数的两个数绝对值相等,即|-a|=|a|。
02
知识精讲
eg:|4|=|-4|,|-|=||,|-4.5|=|4.5|。
绝对值与相反数
思考——若|a|=|b|,那么a与b有怎样的关系?
a=b或a=-b
02
知识精讲
绝对值与相反数
若两个数的绝对值相等,则这两个数相等或互为相反数,即若|a|=|b|,则a=±b。
例1、填空:
(1)a的相反数是____,-a的相反数是____;
(2)a+b的相反数是________________,
a-b的相反数是________________。
(3)正数的相反数都是____;负数的相反数都是____。
-a
a
-(a+b)=-a-b
-(a-b)=-a+b
03
典例精析
负数
正数
例2、下列说法正确的有________(填序号)。
①符号不同的两个数是相反数
②互为相反数的两个数必为一正一负
③12的相反数是21
④2与2.75都是-的相反数
⑤互为相反数的两个数一定不相等
⑥所有的有理数都有相反数
⑦一个数的相反数一定是非正数
⑧一个数可以小于它的相反数
0的相反数是0
只有
12的相反数是-12
03
典例精析
0的相反数是0
负数的相反数是正数
④⑥⑧
例3、如图,图中数轴的单位长度为1,请回答下列问题:
(1)如果点A、B表示的数互为相反数,那么点C表示的数是_____;
(2)如果点E、B表示的数互为相反数,那么点D表示的数是_____。
(1)∵A、B互为相反数,
∴A、B关于原点对称;
-1
-5
A
B
C
D
E
0
0
(2)∵E、B互为相反数,
∴E、B关于原点对称。
03
典例精析
例4-1、若|x|=7,则x=______;
若|-x|=7,则x=______;
若|x|=|7|,则x=______;
若|-x|=|7|,则x=______;
若|-x|=|-7|,则x=______。
±7
±7
±7
|-x|=7,即|x|=7
03
典例精析
|x|=|7|,即|x|=7
±7
|-x|=|7|,即|x|=7
±7
|-x|=|-7|,即|x|=7
例4-2、下列关系一定成立的是( )
A. 若|m|=|n|,则m=n
B. 若|m|=|n|,则m=-n
C. 若|m|>|n|,则m>n
D. 若m=-n,则|m|=|n|
D
03
典例精析
|-a|=|a|;
若|a|=|b|,则a=±b。
多重符号的化简
【分析】
-(-4)表示-4的相反数,
∵-4的相反数是4,
∴-(-4)=4。
尝试——1.化简:-(-4)。
01
课堂引入
对于任意的数a都有-(-a)=a,即一个数的相反数的相反数就是这个数本身。
2.算一算,找规律:
1个“+”:+5=5;
2个“+”:+(+5)=________;
3个“+”:+[+(+5)]=________;
4个“+”:+{+[+(+5)]}=________。
5
5
5
01
课堂引入
“+”号的个数不影响化简的结果,可以直接省略。
3.算一算,找规律:
1个“-”:-5=-5;
2个“-”:-(-5)=________;
3个“-”:-[-(-5)]=________;
4个“-”:-{-[-(-5)]}=________。
5
-5
5
“-”号的个数是奇数时,结果为负;
“-”号的个数是偶数时,结果为正。
01
课堂引入
①对于任意的数a都有-(-a)=a,即一个数的相反数的相反数就是这个数本身。
②“+”号的个数不影响化简的结果,可以直接省略。
③“-”号的个数决定最后化简的结果:
“-”号的个数是奇数时,结果为负;
“-”号的个数是偶数时,结果为正。
(口诀:奇负偶正)
02
知识精讲
多重符号的化简
例、(1)-(-a)=_____,-[+(-a)]=_____,-[-(x+y)]=_____;
(2)-[-(+43)]=_____,-[-(-0.5)]=_____;
(3)-{+[-(+3)]}=_____,-{-[+(-2.6)]}=_____。
a
a
x+y
43
-0.5
3
-2.6
03
典例精析
相反数的性质与判定
→
借
250元
+250
01
课堂引入
→
还
250元
-250
借250,还250,还欠钱吗?
(+250)+(-250)=0,不欠钱。
(+2)+(-2)=0
(+10)+(-10)=0
借2,还2,
不欠钱
借10,还10,
不欠钱
01
课堂引入
02
知识精讲
相反数的性质与判定
①性质:互为相反数的两个数,和为0,
符号语言:若x与y互为相反数,则x+y=0(即x=-y)。
②判定:若两个数的和为0,则这两个数互为相反数,
若x+y=0(即x=-y),则x与y互为相反数。
例1、(1)若m与n互为相反数,则3m+3n+2=_______;
(2)若2m与m-3互为相反数,则m的值为_______。
解:(1)∵m与n互为相反数,
∴m+n=0,
∴3m+3n+2=3(m+n)+2=2;
2
1
(2)∵2m与m-3互为相反数,
∴2m+m-3=0,
∴m=1。
03
典例精析
例2、在①+(+3)与-(-3);②-(+3)与+(-3);③+(+3)与-(+3);④+(-3)与-(-3),互为相反数的是________。(填序号)
【分析】先化简后判断:
①3与3,不互为相反数;②-3与-3,不互为相反数;
③3和-3,互为相反数;④-3和3,互为相反数。
③④
03
典例精析
例3、下列各代数式:①a-b与-a-b;②a+b与-a-b;③a+1与1-a;④-a+b与a-b。其中互为相反数的有( )
A.①②
B.②④
C.②③④
D.①②③④
B
【分析】
若x+y=0(即x=-y),则x与y互为相反数。
①a-b+(-a-b)=-2b不一定等于0;②a+b+(-a-b)=0;
③a+1+(1-a)=2≠0;④-a+b+(a-b)=0。
03
典例精析
课后总结
相反数的概念:
只有符号不同的两个数互为相反数(opposite number),其中一个数叫做另一个数的相反数。
特别地,0的相反数是0。
相反数的概念也可以表示:符号不同,符号后的数值相同的两个数互为相反数。
求一个数的相反数的方法:
几何角度:求一个数的相反数,就是找这个数关于原点的对称点。
代数角度:求一个数的相反数,就是在这个数的前面添加(或删去)一个“-”号。
绝对值与相反数:
互为相反数的两个数绝对值相等,即|-a|=|a|。
若两个数的绝对值相等,则这两个数相等或互为相反数,即若|a|=|b|,则a=±b。
课后总结
多重符号的化简:
①对于任意的数a都有-(-a)=a,即一个数的相反数的相反数就是这个数本身。
②“+”号的个数不影响化简的结果,可以直接省略。
③“-”号的个数决定最后化简的结果:
“-”号的个数是奇数时,结果为负;“-”号的个数是偶数时,结果为正。
(口诀:奇负偶正)
①性质:互为相反数的两个数,和为0,
符号语言:若x与y互为相反数,则x+y=0(即x=-y)。
②判定:若两个数的和为0,则这两个数互为相反数,
若x+y=0(即x=-y),则x与y互为相反数。
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第2章 有理数
2.3.2绝对值与相反数:相反数
教学目标
理解相反数的概念,会求一个数的相反数
掌握多重符号的化简规律
01
02
能利用相反数的性质和判定解决问题
03
相反数的概念
→
借
250元
-250
+250
01
课堂引入
活动——1.如图,观察数轴上表示-4和4的点的位置以及它们到原点的距离,你有什么发现
-4和4关于原点对称,-4和4到原点的距离相等。
01
课堂引入
1
2
3
4
-4
-1
-2
-3
0
继续观察-3和3,-2和2,-1和1,你能得到相同的结论吗?
-3和3,-2和2,-1和1都关于原点对称,
-3和3,-2和2,-1和1到原点的距离都分别相等。
01
课堂引入
1
2
3
4
-4
-1
-2
-3
0
2.观察下列各组数,你发现了什么
1与-1,2与-2,3与-3,4与-4,+250与-250。
+250 -250
符号不同
数值相同
每组数符号不同,符号后的数值相同。
01
课堂引入
如图,以+250与-250为例:
eg:250与-250互为相反数,也可以说250是-250的相反数,-250是250的相反数。
02
知识精讲
相反数的概念
只有符号不同的两个数互为相反数(opposite number),其中一个数叫做另一个数的相反数。
特别地,0的相反数是0。
∵一个数是由符号部分和符号后的数值部分组成,
∴“只有符号不同”,即“符号不同,符号后的数值相同”。
02
知识精讲
相反数的概念
相反数的概念也可以表示:符号不同,符号后的数值相同的两个数互为相反数。
4的相反数是-4
尝试——写出4,-,-4.5的相反数,并在数轴上画出这些数及其相反数对应的点。
-的相反数是
-4.5的相反数是4.5
1
2
3
4
-4
-1
-2
-3
0
-5
-6
5
02
知识精讲
-
-4.5
4.5
1
2
3
4
-4
-1
-2
-3
0
-5
-6
5
-
-4.5
4.5
02
知识精讲
求一个数的相反数
如图,互为相反数(0除外)的两个点,位于原点的两侧,到原点的距离相等,即关于原点对称。
几何角度:求一个数的相反数,就是找这个数关于原点的对称点。
02
知识精讲
求一个数的相反数
代数角度:求一个数的相反数,就是在这个数的前面添加(或删去)一个“-”号。
eg:4添加一个“-”,变成相反数-4;
-删去一个“-”,变成相反数,
-4.5删去一个“-”,变成相反数4.5。
∵互为相反数的两数只相差一个负号,
∴这两个数在数轴上的对应点到原点的距离相等。
由此,我们得到:
互为相反数的两个数绝对值相等,即|-a|=|a|。
02
知识精讲
eg:|4|=|-4|,|-|=||,|-4.5|=|4.5|。
绝对值与相反数
思考——若|a|=|b|,那么a与b有怎样的关系?
a=b或a=-b
02
知识精讲
绝对值与相反数
若两个数的绝对值相等,则这两个数相等或互为相反数,即若|a|=|b|,则a=±b。
例1、填空:
(1)a的相反数是____,-a的相反数是____;
(2)a+b的相反数是________________,
a-b的相反数是________________。
(3)正数的相反数都是____;负数的相反数都是____。
-a
a
-(a+b)=-a-b
-(a-b)=-a+b
03
典例精析
负数
正数
例2、下列说法正确的有________(填序号)。
①符号不同的两个数是相反数
②互为相反数的两个数必为一正一负
③12的相反数是21
④2与2.75都是-的相反数
⑤互为相反数的两个数一定不相等
⑥所有的有理数都有相反数
⑦一个数的相反数一定是非正数
⑧一个数可以小于它的相反数
0的相反数是0
只有
12的相反数是-12
03
典例精析
0的相反数是0
负数的相反数是正数
④⑥⑧
例3、如图,图中数轴的单位长度为1,请回答下列问题:
(1)如果点A、B表示的数互为相反数,那么点C表示的数是_____;
(2)如果点E、B表示的数互为相反数,那么点D表示的数是_____。
(1)∵A、B互为相反数,
∴A、B关于原点对称;
-1
-5
A
B
C
D
E
0
0
(2)∵E、B互为相反数,
∴E、B关于原点对称。
03
典例精析
例4-1、若|x|=7,则x=______;
若|-x|=7,则x=______;
若|x|=|7|,则x=______;
若|-x|=|7|,则x=______;
若|-x|=|-7|,则x=______。
±7
±7
±7
|-x|=7,即|x|=7
03
典例精析
|x|=|7|,即|x|=7
±7
|-x|=|7|,即|x|=7
±7
|-x|=|-7|,即|x|=7
例4-2、下列关系一定成立的是( )
A. 若|m|=|n|,则m=n
B. 若|m|=|n|,则m=-n
C. 若|m|>|n|,则m>n
D. 若m=-n,则|m|=|n|
D
03
典例精析
|-a|=|a|;
若|a|=|b|,则a=±b。
多重符号的化简
【分析】
-(-4)表示-4的相反数,
∵-4的相反数是4,
∴-(-4)=4。
尝试——1.化简:-(-4)。
01
课堂引入
对于任意的数a都有-(-a)=a,即一个数的相反数的相反数就是这个数本身。
2.算一算,找规律:
1个“+”:+5=5;
2个“+”:+(+5)=________;
3个“+”:+[+(+5)]=________;
4个“+”:+{+[+(+5)]}=________。
5
5
5
01
课堂引入
“+”号的个数不影响化简的结果,可以直接省略。
3.算一算,找规律:
1个“-”:-5=-5;
2个“-”:-(-5)=________;
3个“-”:-[-(-5)]=________;
4个“-”:-{-[-(-5)]}=________。
5
-5
5
“-”号的个数是奇数时,结果为负;
“-”号的个数是偶数时,结果为正。
01
课堂引入
①对于任意的数a都有-(-a)=a,即一个数的相反数的相反数就是这个数本身。
②“+”号的个数不影响化简的结果,可以直接省略。
③“-”号的个数决定最后化简的结果:
“-”号的个数是奇数时,结果为负;
“-”号的个数是偶数时,结果为正。
(口诀:奇负偶正)
02
知识精讲
多重符号的化简
例、(1)-(-a)=_____,-[+(-a)]=_____,-[-(x+y)]=_____;
(2)-[-(+43)]=_____,-[-(-0.5)]=_____;
(3)-{+[-(+3)]}=_____,-{-[+(-2.6)]}=_____。
a
a
x+y
43
-0.5
3
-2.6
03
典例精析
相反数的性质与判定
→
借
250元
+250
01
课堂引入
→
还
250元
-250
借250,还250,还欠钱吗?
(+250)+(-250)=0,不欠钱。
(+2)+(-2)=0
(+10)+(-10)=0
借2,还2,
不欠钱
借10,还10,
不欠钱
01
课堂引入
02
知识精讲
相反数的性质与判定
①性质:互为相反数的两个数,和为0,
符号语言:若x与y互为相反数,则x+y=0(即x=-y)。
②判定:若两个数的和为0,则这两个数互为相反数,
若x+y=0(即x=-y),则x与y互为相反数。
例1、(1)若m与n互为相反数,则3m+3n+2=_______;
(2)若2m与m-3互为相反数,则m的值为_______。
解:(1)∵m与n互为相反数,
∴m+n=0,
∴3m+3n+2=3(m+n)+2=2;
2
1
(2)∵2m与m-3互为相反数,
∴2m+m-3=0,
∴m=1。
03
典例精析
例2、在①+(+3)与-(-3);②-(+3)与+(-3);③+(+3)与-(+3);④+(-3)与-(-3),互为相反数的是________。(填序号)
【分析】先化简后判断:
①3与3,不互为相反数;②-3与-3,不互为相反数;
③3和-3,互为相反数;④-3和3,互为相反数。
③④
03
典例精析
例3、下列各代数式:①a-b与-a-b;②a+b与-a-b;③a+1与1-a;④-a+b与a-b。其中互为相反数的有( )
A.①②
B.②④
C.②③④
D.①②③④
B
【分析】
若x+y=0(即x=-y),则x与y互为相反数。
①a-b+(-a-b)=-2b不一定等于0;②a+b+(-a-b)=0;
③a+1+(1-a)=2≠0;④-a+b+(a-b)=0。
03
典例精析
课后总结
相反数的概念:
只有符号不同的两个数互为相反数(opposite number),其中一个数叫做另一个数的相反数。
特别地,0的相反数是0。
相反数的概念也可以表示:符号不同,符号后的数值相同的两个数互为相反数。
求一个数的相反数的方法:
几何角度:求一个数的相反数,就是找这个数关于原点的对称点。
代数角度:求一个数的相反数,就是在这个数的前面添加(或删去)一个“-”号。
绝对值与相反数:
互为相反数的两个数绝对值相等,即|-a|=|a|。
若两个数的绝对值相等,则这两个数相等或互为相反数,即若|a|=|b|,则a=±b。
课后总结
多重符号的化简:
①对于任意的数a都有-(-a)=a,即一个数的相反数的相反数就是这个数本身。
②“+”号的个数不影响化简的结果,可以直接省略。
③“-”号的个数决定最后化简的结果:
“-”号的个数是奇数时,结果为负;“-”号的个数是偶数时,结果为正。
(口诀:奇负偶正)
①性质:互为相反数的两个数,和为0,
符号语言:若x与y互为相反数,则x+y=0(即x=-y)。
②判定:若两个数的和为0,则这两个数互为相反数,
若x+y=0(即x=-y),则x与y互为相反数。
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
