(苏科版2024)七年级上册 2.3.3绝对值与相反数:绝对值的代数意义与化简求值、根据绝对值比较数的大小 课件(共23张PPT)
文档属性
| 名称 | (苏科版2024)七年级上册 2.3.3绝对值与相反数:绝对值的代数意义与化简求值、根据绝对值比较数的大小 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 40.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-20 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第2章 有理数
2.3.3绝对值与相反数:绝对值的代数意义与化简求值、根据绝对值比较数的大小
教学目标
理解绝对值的代数意义,会化简绝对值
能根据绝对值比较数的大小
01
02
绝对值的代数意义
与化简求值
2.3
01
课堂引入
尝试——根据绝对值和相反数的意义填空,你有什么发现?
(1)|2.3|=_____,||=_____,|6|=_____;
(2)|-5|=_____,-5的相反数是_____,
|-10.5|=_____,-10.5的相反数是_____,
|-|=_____,-的相反数是_____;
(3)|0|=_____。
6
5
5
10.5
-10.5
0
由绝对值和相反数的意义可知:
02
知识精讲
绝对值的代数意义
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0。
注:0的绝对值既是它本身,也是它的相反数。
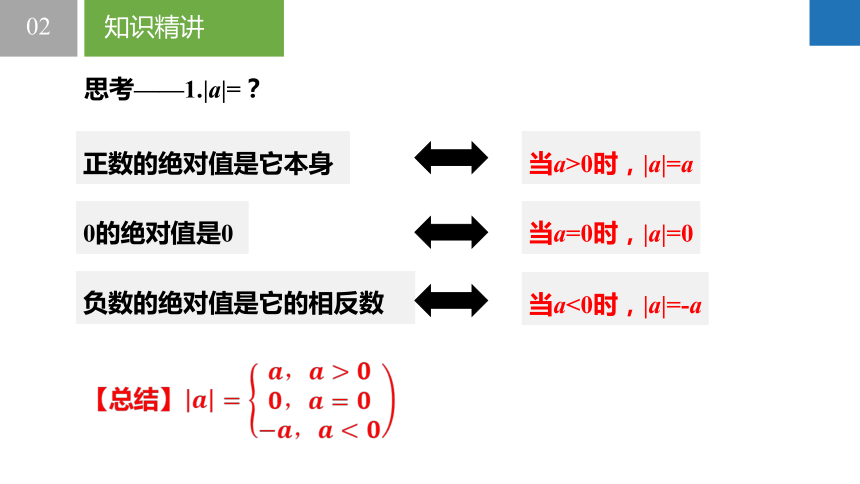
思考——1.|a|=?
当a>0时,|a|=a
当a<0时,|a|=-a
当a=0时,|a|=0
正数的绝对值是它本身
负数的绝对值是它的相反数
0的绝对值是0
02
知识精讲
【总结】
2.绝对值最小的数是_______;
_______的绝对值是它本身;
_______的绝对值是它的相反数。
0
非负数
非正数
02
知识精讲
例1-1、(1)a+b>0,则|a+b|=______;
(2)a+b<0,则|a+b|=______;
(3)-a+b<0,则|-a+b|=______;
(4)-a-b-c>0,则|-a-b-c|=______。
a+b
-(a+b)=-a-b
-(-a+b)=a-b
-a-b-c
【解题技巧】
求一个数的绝对值,首先要分清这个数是正数、负数,还是0,然后才能正确地写出它的绝对值。
03
典例精析
例1-2、2解:∵2∴2-a<0,a-4<0,
∴原式=-2+a+(-a+4)=2。
2
03
典例精析
例2、有理数a、b、c在数轴上的位置如图:
(1)判断正负,用“>”或“<”填空:b-c____0,a+b____0,c-a____0;
(2)化简:|b-c|+|a+b|-|c-a|=________。
<
<
解:(1)可采用赋值法:
设a=-4,b=2,c=6;
>
(2)原式=-b+c+(-a-b)-(c-a)
=-b+c-a-b-c+a
=-2b
-2b
03
典例精析
0
b
a
c
例3-1、已知a是任意有理数,则|-a|-a的值是( )
A. 必大于0
B. 必小于0
C. 必不大于0
D. 必不小于0
【分析】
若a>0,则原式=a-a=0,
若a=0,则原式=0-0=0,
若a<0,则原式=-a-a=-2a>0。
D
03
典例精析
【解题技巧】
求一个数的绝对值,若无法判断这个数是正数、负数,还是0,则需分类讨论。
例3-2、若a≠0,则+1的值为( )
A.2 B.0 C.±1 D.0或2
D
03
典例精析
【分析】
当a>0时,|a|=a,==1,+1=2;
当a<0时,|a|=-a,==-1,+1=0。
【总结】
【分析】
当a、b、c都为“+”时,原式=1+1+1=3;
例3-3、若a,b,c均为非0有理数,则++的值为_________。
±3或±1
03
典例精析
当a、b、c为1个“+”、2个“-”时,
设a>0,b、c<0,原式=1+(-1)+(-1)=-1。
当a、b、c都为“-”时,原式=-1+(-1)+(-1)=-3;
当a、b、c为2个“+”、1个“-”时,
设a、b>0,c<0,原式=1+1+(-1)=1;
根据绝对值比较数的大小
讨论——在两个正数中,绝对值较大的那个数一定大吗?两个负数呢?
1
2
3
4
-4
-1
-2
-3
0
-5
-6
5
3
5
1
2
3
4
-4
-1
-2
-3
0
-5
-6
5
5
3
01
课堂引入
数轴上表示两个正数的点都在原点的右边,绝对值越大越靠右;数轴上表示两个负数的点都在原点的左边,绝对值越大越靠左,因此可得:
02
知识精讲
根据绝对值比较数的大小
两个正数,绝对值大的正数大;
两个负数,绝对值大的负数反而小。
符号语言:
(1)当a>0,b>0时,若|a|>|b|,则a>b;
(2)当a<0,b<0时,若|a|>|b|,则a02
知识精讲
尝试——比较下列各组数的大小:
(1)-3.6与-3.66;(2)-与-。
解:(1)∵|-3.6|=3.6,|-3.66|=3.66,且3.6<3.66,
∴-3.6>3.66;
两个负数,绝对值大的负数反而小。
(2)∵|-|=,|-|=,且>,
∴-<-。
探究——1.当a<2时,|a|也一定小于2吗?
02
知识精讲
1
2
3
4
-4
-1
-2
-3
0
-5
-6
5
2
2
-2a≤-2时,|a|≥2。
2._______的绝对值是不大于它本身;
_______的绝对值是不大于它的相反数。
非负数
非正数
例1、用“>”“<”或“=”填空:
(1)-12.3____-12;
(2)-(-2.75)____-(-2.67);
(3)-|-8|____-8;
(4)-|-0.4|____-(-0.4)。
<
>
=
<
03
典例精析
例2、若有理数a、b在数轴上的位置如图所示。
试比较a,b,-b,|a|的大小,并用“<”号把它们连接起来。
【分析】
∵b与-b互为相反数,
∴b与-b关于原点对称;
综上,a<-b∵a<0,
∴|a|=-a,
∴|a|与a关于原点对称;
0
b
a
-b
|a|
03
典例精析
课后总结
根据绝对值比较数的大小:
两个正数,绝对值大的正数大;
两个负数,绝对值大的负数反而小。
绝对值的代数意义:
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0。
注:0的绝对值既是它本身,也是它的相反数。
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第2章 有理数
2.3.3绝对值与相反数:绝对值的代数意义与化简求值、根据绝对值比较数的大小
教学目标
理解绝对值的代数意义,会化简绝对值
能根据绝对值比较数的大小
01
02
绝对值的代数意义
与化简求值
2.3
01
课堂引入
尝试——根据绝对值和相反数的意义填空,你有什么发现?
(1)|2.3|=_____,||=_____,|6|=_____;
(2)|-5|=_____,-5的相反数是_____,
|-10.5|=_____,-10.5的相反数是_____,
|-|=_____,-的相反数是_____;
(3)|0|=_____。
6
5
5
10.5
-10.5
0
由绝对值和相反数的意义可知:
02
知识精讲
绝对值的代数意义
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0。
注:0的绝对值既是它本身,也是它的相反数。
思考——1.|a|=?
当a>0时,|a|=a
当a<0时,|a|=-a
当a=0时,|a|=0
正数的绝对值是它本身
负数的绝对值是它的相反数
0的绝对值是0
02
知识精讲
【总结】
2.绝对值最小的数是_______;
_______的绝对值是它本身;
_______的绝对值是它的相反数。
0
非负数
非正数
02
知识精讲
例1-1、(1)a+b>0,则|a+b|=______;
(2)a+b<0,则|a+b|=______;
(3)-a+b<0,则|-a+b|=______;
(4)-a-b-c>0,则|-a-b-c|=______。
a+b
-(a+b)=-a-b
-(-a+b)=a-b
-a-b-c
【解题技巧】
求一个数的绝对值,首先要分清这个数是正数、负数,还是0,然后才能正确地写出它的绝对值。
03
典例精析
例1-2、2
∴原式=-2+a+(-a+4)=2。
2
03
典例精析
例2、有理数a、b、c在数轴上的位置如图:
(1)判断正负,用“>”或“<”填空:b-c____0,a+b____0,c-a____0;
(2)化简:|b-c|+|a+b|-|c-a|=________。
<
<
解:(1)可采用赋值法:
设a=-4,b=2,c=6;
>
(2)原式=-b+c+(-a-b)-(c-a)
=-b+c-a-b-c+a
=-2b
-2b
03
典例精析
0
b
a
c
例3-1、已知a是任意有理数,则|-a|-a的值是( )
A. 必大于0
B. 必小于0
C. 必不大于0
D. 必不小于0
【分析】
若a>0,则原式=a-a=0,
若a=0,则原式=0-0=0,
若a<0,则原式=-a-a=-2a>0。
D
03
典例精析
【解题技巧】
求一个数的绝对值,若无法判断这个数是正数、负数,还是0,则需分类讨论。
例3-2、若a≠0,则+1的值为( )
A.2 B.0 C.±1 D.0或2
D
03
典例精析
【分析】
当a>0时,|a|=a,==1,+1=2;
当a<0时,|a|=-a,==-1,+1=0。
【总结】
【分析】
当a、b、c都为“+”时,原式=1+1+1=3;
例3-3、若a,b,c均为非0有理数,则++的值为_________。
±3或±1
03
典例精析
当a、b、c为1个“+”、2个“-”时,
设a>0,b、c<0,原式=1+(-1)+(-1)=-1。
当a、b、c都为“-”时,原式=-1+(-1)+(-1)=-3;
当a、b、c为2个“+”、1个“-”时,
设a、b>0,c<0,原式=1+1+(-1)=1;
根据绝对值比较数的大小
讨论——在两个正数中,绝对值较大的那个数一定大吗?两个负数呢?
1
2
3
4
-4
-1
-2
-3
0
-5
-6
5
3
5
1
2
3
4
-4
-1
-2
-3
0
-5
-6
5
5
3
01
课堂引入
数轴上表示两个正数的点都在原点的右边,绝对值越大越靠右;数轴上表示两个负数的点都在原点的左边,绝对值越大越靠左,因此可得:
02
知识精讲
根据绝对值比较数的大小
两个正数,绝对值大的正数大;
两个负数,绝对值大的负数反而小。
符号语言:
(1)当a>0,b>0时,若|a|>|b|,则a>b;
(2)当a<0,b<0时,若|a|>|b|,则a
知识精讲
尝试——比较下列各组数的大小:
(1)-3.6与-3.66;(2)-与-。
解:(1)∵|-3.6|=3.6,|-3.66|=3.66,且3.6<3.66,
∴-3.6>3.66;
两个负数,绝对值大的负数反而小。
(2)∵|-|=,|-|=,且>,
∴-<-。
探究——1.当a<2时,|a|也一定小于2吗?
02
知识精讲
1
2
3
4
-4
-1
-2
-3
0
-5
-6
5
2
2
-2
2._______的绝对值是不大于它本身;
_______的绝对值是不大于它的相反数。
非负数
非正数
例1、用“>”“<”或“=”填空:
(1)-12.3____-12;
(2)-(-2.75)____-(-2.67);
(3)-|-8|____-8;
(4)-|-0.4|____-(-0.4)。
<
>
=
<
03
典例精析
例2、若有理数a、b在数轴上的位置如图所示。
试比较a,b,-b,|a|的大小,并用“<”号把它们连接起来。
【分析】
∵b与-b互为相反数,
∴b与-b关于原点对称;
综上,a<-b
∴|a|=-a,
∴|a|与a关于原点对称;
0
b
a
-b
|a|
03
典例精析
课后总结
根据绝对值比较数的大小:
两个正数,绝对值大的正数大;
两个负数,绝对值大的负数反而小。
绝对值的代数意义:
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0。
注:0的绝对值既是它本身,也是它的相反数。
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
